Funciones de variable compleja

Curvas en el plano complejo

z(t)=x(t)+i·y(t) con a≤t≤b describe una curva en el plano complejo dependiente de un parámetro t que va desde z(a)=x(a)+i·y(a) hasta z(b)=x(b)+i·y(b). Si z(a)=z(b) la curva es cerrada.

La ecuación del segmento de una recta que une los puntos z₀y z₁ es

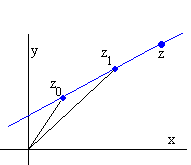
z=z₀+(z₁-z₀)·t con 0≤t≤1.

La ecuación de la recta que une los puntos z₀ y z₁es

z=z₀+(z₁-z₀)·t con -∞<t<∞.

La ecuación de la recta paralela al eje Y que pasa por x₀=1 es z=1+i·y, con -∞<y<∞.

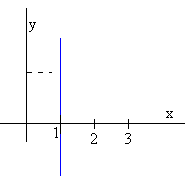
Los puntos de una circunferencia z equidistan de su centro z₀ una longitud igual a su radio r, de modo que |z-z₀|=r

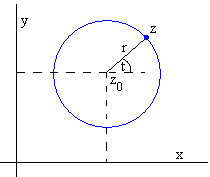
Una circunferencia centrada en z₀ y de radio r tiene la siguiente ecuación

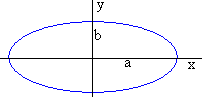
$\begin{array}{l} z = z_{0} + r (\cos t + i \sin t) 0 \leq t \leq 2 π \\ z = z_{0} + r \exp (i t) 0 \leq t \leq 2 π \end{array}$

La ecuación de una elipse centrda en el origen y de semiejes a y b se escribe

z=a·cos(t)+i·b·sin(t), con 0≤t≤2π

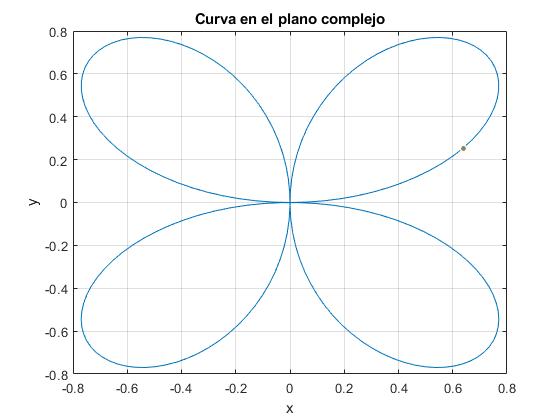
Dibujamos la curva cerrada z(t)=sin(2t)·cos(t)+i·sin(2t)·cos(t) con 0≤t≤2π

t=linspace(0,2*pi,200);
z=sin(2*t).*(cos(t)+1i*sin(t));
plot(z)
grid on
xlabel('x')
ylabel('y')
title('Curva en el plano complejo')

Funciones de variable compleja

La expresión z²-(2+i)z se puede evaluar para cualquier número complejo z y da como resultado un número complejo. Definimos la función f(z)=z²-(2+i)z y calculamos el valor de la función por ejemplo, para z=1+i.

f(1+i)=(1+i)²-(2+i)·(1+i)=-1-i

>> f=@(z) z^2-(2+1i)*z;
>> f(1+1i)
ans =  -1.0000 - 1.0000i

La expresión i+2·Re(z) también define una función de variable compleja. Definimos la función g(z)=i+2·Re(z) y calculamos el valor de la función, por ejemplo, para z=i.

g(i)=i+2·Re(i)=i+2·0=i

>> g=@(z) 1i+real(z);
>> g(1i)
ans = 0 + 1.0000i

Expresamos una función f(z) de variable compleja en términos de dos funciones u(x,y) y v(x,y) de variable real

f(z)=f(x+iy)=u(x,y)+i·v(x,y)

Por ejmplo, la función f(z)=z²=(x+iy)²=x²-y²+2xyi. Así pues, u(x,y)==x²-y² y v(x,y)=2xy

>>  syms x y z;
>> f=z^2;
>> fxy=subs(f,z,x+1i*y)
fxy =(x + y*1i)^2
>> expand(fxy)
ans =x^2 + x*y*2i - y^2

En una función de variable real y=f(x) a la abscisa x le correponde la ordenada y. Una gráfica de la función y=f(x) en el intervalo a<x<b está definida por el conjunto de puntos (x,f(x)) del plano.

Sin embargo, w=f(z) es una función de variable compleja. A cada punto del plano z=x+iy le corresponde un punto del plano w=u+iv que denominaremos imagen.

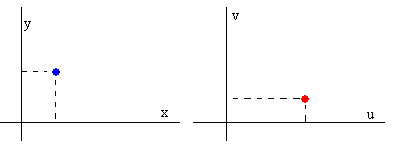
Transformada de una recta paralela al eje Y, w=z²

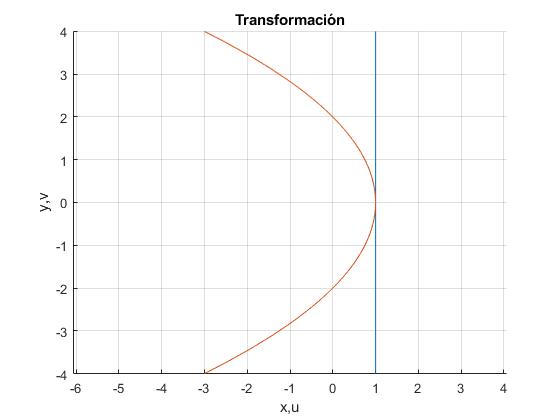
Sea la recta paralela al eje Y, x=1 (en color azul en la figura), vamos a determinar como sería su imagen bajo la transformación w=z² (en color rojo en la figura)

La ecuación de los puntos de la recta es z=1+iy. Por lo que w=z²=(1+iy)²=1-y²+2yi

u=1-y², v=2y con -∞<y<∞. Se trata de la ecuación de una curva dependiente del parámetro y. Eliminamos y, y obtenemos la ecuación de una parábola en el plano u,v.

$u = 1 - \frac{v^{2}}{4}$

syms y;
z=1+1i*y; %recta
w=z^2; %imagen
hold on
fplot(real(z),imag(z),[-4,4])
fplot(real(w),imag(w),[-2,2]);
hold off
grid on
axis equal
title('Transformación')
ylabel('y,v')
xlabel('x,u')

Transformada de una recta paralela al eje Y, $w = \sqrt{z}$

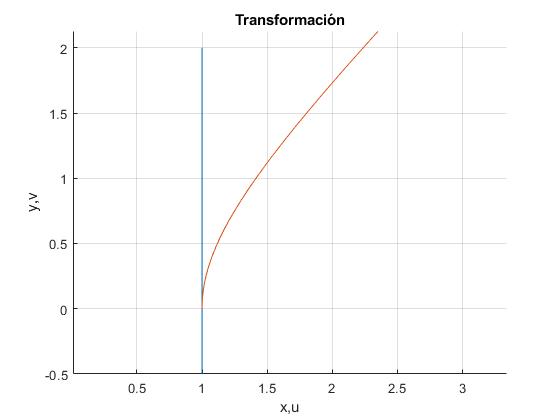
Sea la recta paralela al eje Y, x=a (en color azul en la figura), vamos a determinar como sería su imagen bajo la transformación $w = \sqrt{z}$ (en color rojo en la figura)

La ecuación de los puntos de la recta es z=a+iy, con a=1.

$\begin{array}{l} u + i v = \sqrt{x + i y} \\ u^{2} - v^{2} + 2 i u v = x + i y {\begin{cases} x = u^{2} - v^{2} \\ y = 2 u v \end{cases} \\ {\begin{cases} a = u^{2} - v^{2} \\ y = 2 u v \end{cases} \end{array}$

Obtenemos la ecuación de una hipérbola, probar cuando a es negativo o nulo.

syms y;
a=1;
z=a+1i*y; %recta
w=sqrt(z); %imagen
hold on
fplot(real(z),imag(z),[-0.5,2])
fplot(real(w),imag(w),[0,10]);
hold off
grid on
axis equal
title('Transformación')
ylabel('y,v')
xlabel('x,u')

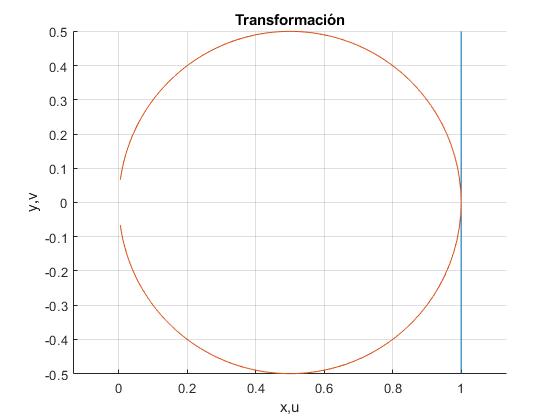
Transformada de una recta paralela al eje Y, w=1/z

$w = \frac{1}{z} = \frac{1}{1 + i y} = \frac{1}{1 + y^{2}} - \frac{y}{1 + y^{2}} i {\begin{cases} u = \frac{1}{1 + y^{2}} \\ v = - \frac{y}{1 + y^{2}} \end{cases}$

Eliminamos y para realacionar u y v.

$\begin{array}{l} y = \frac{- v}{u} u = \frac{1}{1 + {(- v / u)}^{2}} \\ u^{2} + v^{2} - u = 0 \\ {(u - \frac{1}{2})}^{2} + v^{2} = \frac{1}{4} \end{array}$

La transformada es una circunferencia centrada en u=1/2, v=0 y de radio 1/2

syms y;
z=1+1i*y; %recta
w=1/z; %imagen
hold on
fplot(real(z),imag(z),[-0.5,0.5])
fplot(real(w),imag(w),[-15,15]);
hold off
grid on
axis equal
title('Transformación')
ylabel('y,v')
xlabel('x,u')

El parámetro y se extiende desde -∞ a +∞, pero fplot no dibuja bien la circunferencia para valores grandes de y.

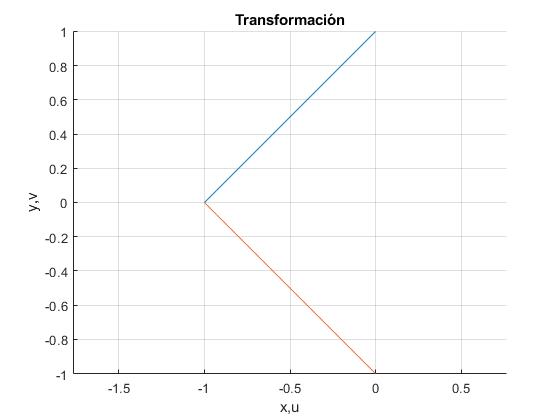
Transformada de un segmento de recta, w=iz

La ecuación de la recta que une los puntos z₀=-1 y z₁=i es z=-1+(i+1)t con 0≤t≤1.

Transformamos este segmento de recta mediante la función w=iz

w=-i+(-1+i)·t

que es un segmento de recta que pasa por z₀=-i, z₁=-1, tal como vemos en la figura (en color rojo)

syms t;
z=-1+(1i+1)*t; %recta
w=1i*z; %imagen
hold on
fplot(real(z),imag(z),[0,1])
fplot(real(w),imag(w),[0,1]);
hold off
grid on
axis equal
title('Transformación')
ylabel('y,v')
xlabel('x,u')

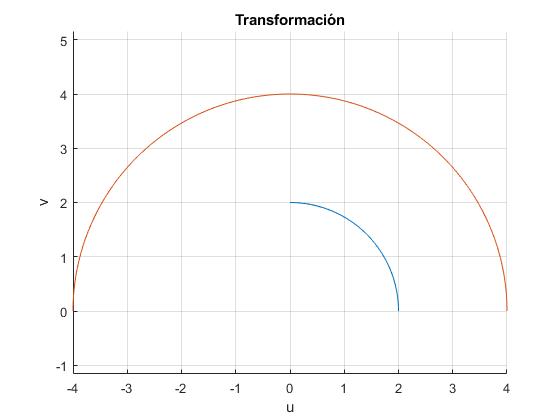
Transformada de un arco de circunferencia, w=z²

Vamos a transformar un cuadrante de la circunferencia centrada en el origen y de radio r=2, mediante la función w=z²

$\begin{array}{l} z = r \cdot \exp (i θ) \\ z^{2} = r^{2} \exp (i 2 θ) \end{array}$

Cada punto del arco de circunferencia de radio r=2 y de extensión 0≤θ≤π/2, (en color azul), cuando se transforma adquiere un módulo de r=2²=4, el argumento θ del punto pasa a valer 2θ después de la transformación. El resultado final es un arco de circunferencia de radio r=4 que se extiende de 0≤θ≤π es decir, una semicircuferencia.

syms t;
z=2*(cos(t)+1i*sin(t)); %arco 
w=z^2;  %imagen
hold on
fplot(real(z),imag(z),[0,pi/2]); 
fplot(real(w),imag(w),[0,pi/2]); 
hold off
grid on
axis equal
title('Transformación')
ylabel('v')
xlabel('u')

Transformación lineal

Las transformaciones más importantes son: traslación, rotación y ampliación

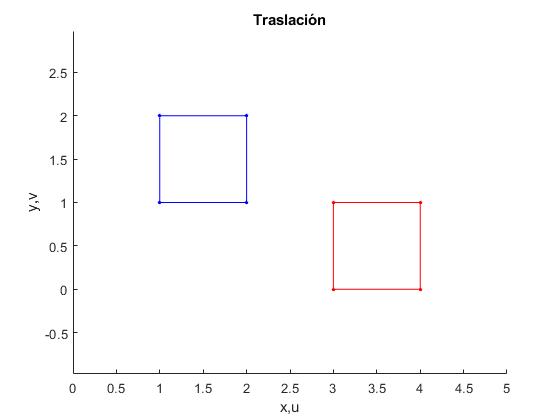
Traslación

Una traslación es la transformación lineal T(z)=z+b

T(z)=(x+iy)+(x₀+iy₀)=x+x₀+i(y+y₀)

Sea el cuadrado de vértices 1+i, 2+i, 2+2i,1+2i en color azul en la figura de la izquierda . Lo trasladamos mediante la transformación T(z)=z+2-i, obtenemos el cuadrado de vértices 3, 4, 4+i, 3+i que vemos de color rojo en la figura de la derecha.

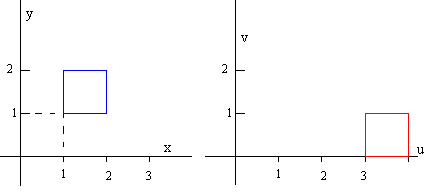
T=@(z) z+(2-1i); 
sq=[1+1i,2+1i,2+2*1i,1+2*1i]
sqt=T(sq)
hold on
plot(real(sq),imag(sq),'bo','markersize',2,'markerfacecolor','b')
plot(real(sqt),imag(sqt),'ro','markersize',2,'markerfacecolor','r')

sq=[sq,sq(1)];  %para cerrar el cuadrado
sqt=[sqt,sqt(1)];
plot(real(sq),imag(sq),'b')
plot(real(sqt),imag(sqt),'r')
hold off
axis equal
xlim([0,5])
title('Traslación')
xlabel('x,u')
ylabel('y,v')

En la ventana de comandos vemos el resultado de la transformación.

sq =   1.0000 + 1.0000i   2.0000 + 1.0000i   2.0000 + 2.0000i   1.0000 + 2.0000i
sqt =   3.0000             4.0000             4.0000 + 1.0000i   3.0000 + 1.0000i

Rotación

Una rotación es la transformación R(z)=az con |a|=1

En forma polar escribimos

$R (z) = \exp (i θ) \cdot r \exp (i φ) = r \cdot \exp (i (θ + φ))$

Se trata de un número complejo del mismo módulo r que z pero cuyo argumento es θ+φ.

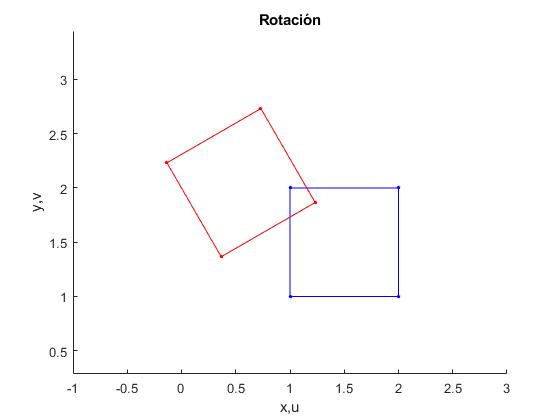
Sea el cuadrado de vértices 1+i, 2+i, 2+2i,1+2i en color azul. Lo rotamos mediante la transformación

$R (z) = (\frac{\sqrt{3}}{2} + i \frac{1}{2}) z = \exp (i \frac{π}{6}) z$

Obtenemos el cuadrado de color rojo de la figura girando π/6 (30°) alrededor del origen, cada uno de los vértices del cuadrado de color azul en el sentido contrario a las agujas del reloj.

R=@(z) (sqrt(3)+1i)*z/2; 
sq=[1+1i,2+1i,2+2*1i,1+2*1i]
sqt=R(sq)
hold on
plot(real(sq),imag(sq),'bo','markersize',2,'markerfacecolor','b')
plot(real(sqt),imag(sqt),'ro','markersize',2,'markerfacecolor','r')
sq=[sq,sq(1)];
sqt=[sqt,sqt(1)];
plot(real(sq),imag(sq),'b')
plot(real(sqt),imag(sqt),'r')
hold off
axis equal
xlim([-1,3])
title('Rotación')
xlabel('x,u')
ylabel('y,v')

En la ventana de comandos vemos el resultado de la transformación

sq =   1.0000 + 1.0000i   2.0000 + 1.0000i   2.0000 + 2.0000i   1.0000 + 2.0000i
sqt =   0.3660 + 1.3660i   1.2321 + 1.8660i   0.7321 + 2.7321i  -0.1340 + 2.2321i

Ampliación

Una ampliación es la transformación M(z)=az con a>0

En forma polar escribimos

$M (z) = a (r \exp (i θ)) = (a r) \exp (i θ)$

El módulo del número complejo z se multiplica por el número real a, pero el argumento no cambia

Sea el cuadrado centrado en el origen de vértices 1/2+i/2, -1/2+i/2, -1/2-i/2,1/2-i/2 en color azul. Lo ampliamos tres veces mediante la transformación M(z)=3·z

M=@(z) 3*z; 
sq=[1+1i,-1+1i,-1-1i,1-1i]/2
sqt=M(sq)
hold on
plot(real(sq),imag(sq),'bo','markersize',2,'markerfacecolor','b')
plot(real(sqt),imag(sqt),'ro','markersize',2,'markerfacecolor','r')
sq=[sq,sq(1)];
sqt=[sqt,sqt(1)];
plot(real(sq),imag(sq),'b')
plot(real(sqt),imag(sqt),'r')
hold off
axis equal
xlim([-2,2])
title('Ampliación')
xlabel('x,u')
ylabel('y,v')

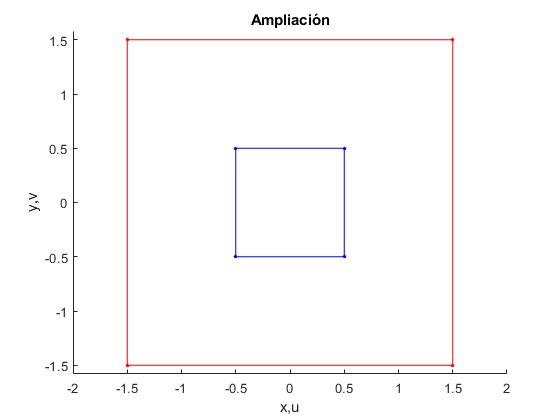
En la ventana de comandos vemos el resultado de la transformación

sq =   0.5000 + 0.5000i  -0.5000 + 0.5000i  -0.5000 - 0.5000i   0.5000 - 0.5000i
sqt =   1.5000 + 1.5000i  -1.5000 + 1.5000i  -1.5000 - 1.5000i   1.5000 - 1.5000i

Sea el cuadrado de vértices 1+i, 2+i, 2+2i,1+2i en color azul, este cuadrado no está centrado en el origen. El resultado de aplicar la transformación Ampliación M(z)=3·z es el siguiente:

M=@(z) 3*z; 
sq=[1+1i, 2+1i, 2+2i,1+2i];
sqt=M(sq);
hold on
plot(real(sq),imag(sq),'bo','markersize',2,'markerfacecolor','b')
plot(real(sqt),imag(sqt),'ro','markersize',2,'markerfacecolor','r')
sq=[sq,sq(1)];
sqt=[sqt,sqt(1)];
plot(real(sq),imag(sq),'b')
plot(real(sqt),imag(sqt),'r')
hold off
axis equal
title('Ampliación')
xlabel('x,u')
ylabel('y,v')

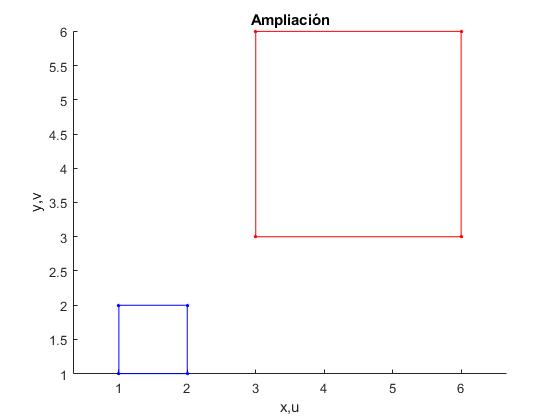
Transformación lineal

Una transformación lineal es una combinación de rotación, traslación y ampliación.

$f (z) = a z + b = | a | (\frac{a}{| a |} z) + b = | a | (\exp (i θ) \cdot z) + b$

la ampliación es el módulo de a,
la rotación un ángulo θ es el argumento de a,
la traslación es b.

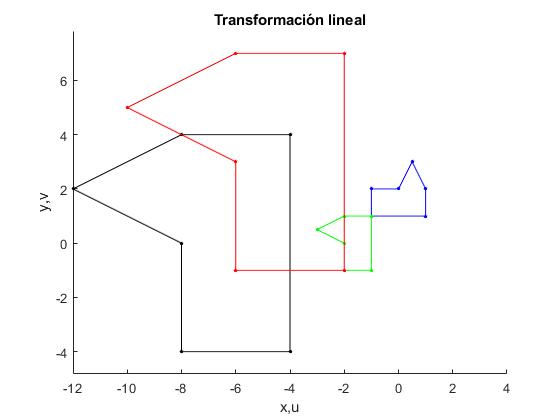
Sea el polígono de vértices -1+i, 1+i, 1+2i, 1/2+3i, 2i,-1+2i, se le aplica la transformación lineal f(z)=4iz+(2+3i)

En primer lugar, aplicamos la transformación Rotación R(z). Giramos el rectángulo inicial (en color azul), π(90°) el resultado lo dibujamos en color verde.
A continuación, aplicamos la transformación Ampliación M(z). Ampliamos cuatro veces el rectángulo resultante, el resultado lo dibujamos en color negro.
Finalmente, aplicamos la transformación Traslación T(z). Trasladamos el rectángulo b=2+3i, el resultado lo dibujamos en color rojo.

%f=@(z) 4*i*z+2+3*i; %transformación lineal
R=@(z) 1i*z;  %rotación
M=@(z) 4*z;  %ampliación
T=@(z) z+(2+3*1i); %traslación

r=[-1+1i,1+1i,1+2*1i,1/2+3*1i,2*1i,-1+2*1i];
hold on
%rectángulo inicial
plot(real(r),imag(r),'bo','markersize',2,'markerfacecolor','b')
s=[r,r(1)];
plot(real(s),imag(s),'b')

%rotación
rt=R(r);
plot(real(rt),imag(rt),'go','markersize',2,'markerfacecolor','g')
s=[rt,rt(1)];
plot(real(s),imag(s),'g')

%ampliación
rt=M(rt);
plot(real(rt),imag(rt),'ko','markersize',2,'markerfacecolor','k')
s=[rt,rt(1)];
plot(real(s),imag(s),'k')

%traslación
rt=T(rt);
plot(real(rt),imag(rt),'ro','markersize',2,'markerfacecolor','r')
s=[rt,rt(1)];
plot(real(s),imag(s),'r')

hold off
axis equal
xlim([-12,4])
title('Transformación lineal')
xlabel('x,u')
ylabel('y,v')

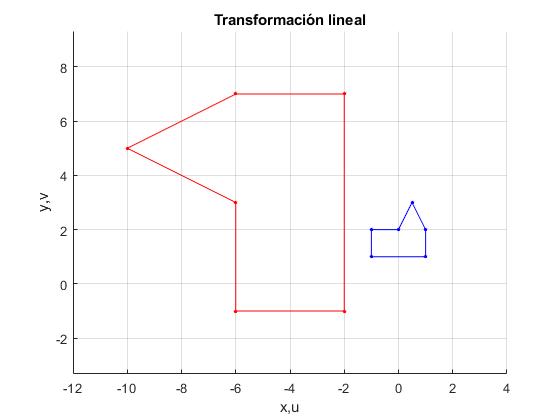
Eliminamos los pasos intermedios y dibujamos el rectángulo inicial y el resultado de aplicarle la transformación lineal f(z)=4iz+(2+3i).

f=@(z) 4*1i*z+2+3*1i; %transformación lineal

hold on
r=[-1+1i,1+1i,1+2*1i,1/2+3*1i,2*1i,-1+2*1i];
%rectángulo inicial
plot(real(r),imag(r),'bo','markersize',2,'markerfacecolor','b')
s=[r,r(1)];
plot(real(s),imag(s),'b')

%transformación lineal
rt=f(r);
plot(real(rt),imag(rt),'ro','markersize',2,'markerfacecolor','r')
s=[rt,rt(1)];
plot(real(s),imag(s),'r')

hold off
grid on
axis equal
xlim([-12,4])
title('Transformación lineal')
xlabel('x,u')
ylabel('y,v')

Ejercicio

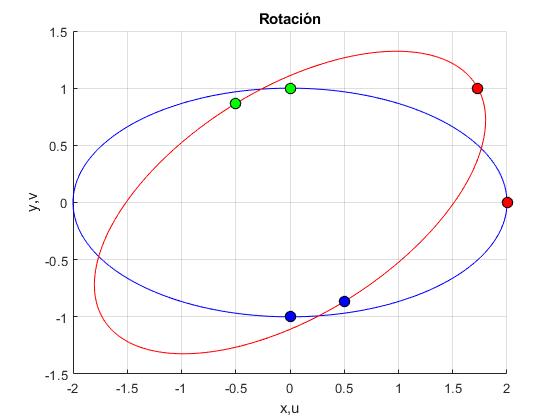
Dibujar una elipse de semiejes 2 y 1 centrada en el origen. Girarla 30° en el sentido contrario a las agujas del reloj

f=@(t) 2*cos(t)+1i*sin(t);
t=(0:360)*pi/180;
hold on
plot(real(f(t)),imag(f(t)),'b') %original
fg=exp(1i*pi/6)*f(t);
plot(real(fg),imag(fg),'r');  %girada

color=['r','g','b']; %tres puntos
z=[2,1i,-1i];
z1=z*exp(1i*pi/6);
for k=1:length(z)
    plot(real(z(k)),imag(z(k)),'ko','markersize',8,'markerfacecolor',color(k));
    plot(real(z1(k)),imag(z1(k)),'ko','markersize',8,'markerfacecolor',color(k));
end
hold off
grid on
xlabel('x,u')
ylabel('y,v')
title('Rotación')

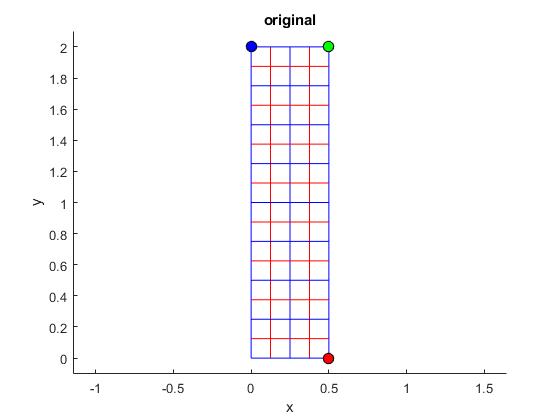
En estos ejemplos, veremos el aspecto de la imagen (u,v) de una rejilla en el plano (x,y) como resultado de la aplicación de varias transformaciones w=f(z)

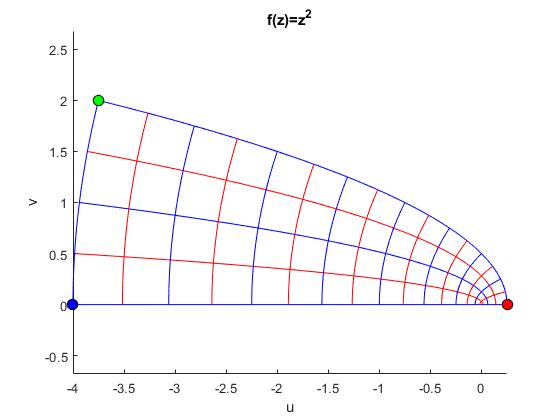
w=z²

En sección anterior, ya hemos visto la imagen bajo esta transformación de una recta paralela al eje Y, el resultado era una parábola.

hold on
for x=0:0.25:0.5  %líneas horizontales
    line([x,x],[0,2],'color','b')
end
for x=0.125:0.25:0.5-0.125
    line([x,x],[0,2],'color','r');
end
for y=0:0.25:2   %líneas verticales
    line([0,0.5],[y,y],'color','b')
end
for y=0.125:0.25:2-0.125
    line([0,0.5],[y,y],'color','r');
end
x=[0.5,0.5,0];   %tres puntos
y=[0,2,2];
color=['r','g','b'];
for k=1:length(x)
    plot(x(k),y(k),'ko','markersize',8,'markerfacecolor',color(k)) 
end
hold off
axis equal
ylim([-0.1,2.1])
xlabel('x')
ylabel('y')
title('original')

syms x y z;
f=z^2;
hold on
x=0:0.25:0.5;  %líneas horizontales
z1=x+1i*y;
ff=subs(f,z,z1);
for k=1:length(x)
    fplot(real(ff(k)),imag(ff(k)),[0,2],'color','b')
end
x=0.125:0.25:0.5-0.125;
z1=x+1i*y;
ff=subs(f,z,z1);
for k=1:length(x)
    fplot(real(ff(k)),imag(ff(k)),[0,2],'color','r');
end
clear x;
syms x;
y=0:0.25:2;   %líneas verticales
z1=x+1i*y;
ff=subs(f,z,z1);
for k=1:length(y)
    fplot(real(ff(k)),imag(ff(k)),[0,0.5],'color','b')
end
y=0.125:0.25:2-0.125;
z1=x+1i*y;
ff=subs(f,z,z1);
for k=1:length(y)
    fplot(real(ff(k)),imag(ff(k)),[0,0.5],'color','r');
end

z1=[1/2,1/2+2*1i,2*1i];   %tres puntos
ff=subs(f,z,z1);
color=['r','g','b'];
for k=1:length(z1)
    plot(real(ff(k)),imag(ff(k)),'ko','markersize',8,'markerfacecolor',color(k)) 
end
hold off
axis equal
xlabel('u')
ylabel('v')
title('f(z)=z^2')

$w = \sqrt{z}$

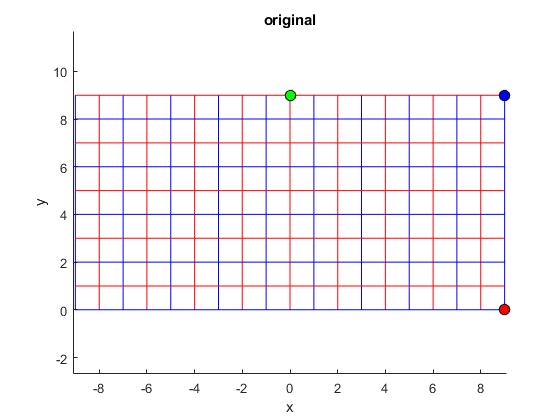
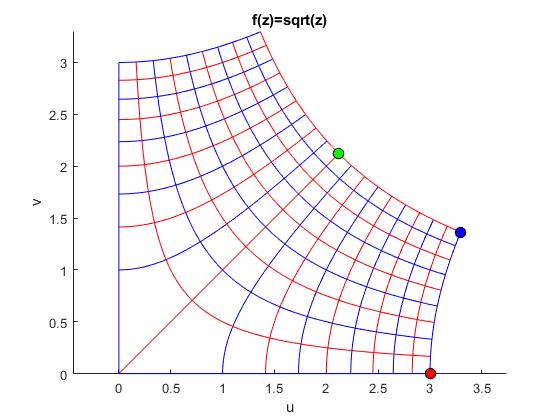
En la página anterior, ya hemos visto la imagen bajo esta transformación de una recta paralela al eje Y, el resultado era una hipérbola.

hold on
for x=-9:2:9; %líneas verticales
    line([x,x],[0,9],'color','b')
end
for x=-8:2:8;
    line([x,x],[0,9],'color','r');
end
for y=0:2:8; %líneas horizontales
    line([-9,9],[y,y],'color','b')
end
for y=1:2:9;
    line([-9,9],[y,y],'color','r');
end

x=[9,0,9];   %tres puntos
y=[0,9,9];
color=['r','g','b'];
for k=1:length(x)
    plot(x(k),y(k),'ko','markersize',8,'markerfacecolor',color(k)) 
end
hold off
axis equal
xlim([-9.1,9.1])
xlabel('x')
ylabel('y')
title('original')

syms x y z;
f=sqrt(z);
hold on
x=-9:2:9; %líneas verticales
z1=x+1i*y;
ff=subs(f,z,z1);
for k=1:length(x)
    fplot(real(ff(k)),imag(ff(k)),[0,9],'color','b')
end
x=-8:2:8;
z1=x+1i*y;
ff=subs(f,z,z1);
for k=1:length(x)
    fplot(real(ff(k)),imag(ff(k)),[0,9],'color','r');
end
clear x;
syms x;
y=0:2:8; %líneas horizonatales
z1=x+1i*y;
ff=subs(f,z,z1);
for k=1:length(y)
    fplot(real(ff(k)),imag(ff(k)),[-9,9],'color','b')
end
y=1:2:9;
z1=x+1i*y;
ff=subs(f,z,z1);
for k=1:length(y)
    fplot(real(ff(k)),imag(ff(k)),[-9,9],'color','r');
end

z1=[9,9*1i,9+9*1i]; %tres puntos
ff=subs(f,z,z1);
color=['r','g','b'];
for k=1:length(z1)
    plot(real(ff(k)),imag(ff(k)),'ko','markersize',8,'markerfacecolor',color(k)) 
end
hold off
axis equal
xlabel('u')
ylabel('v')
title('f(z)=sqrt(z)')

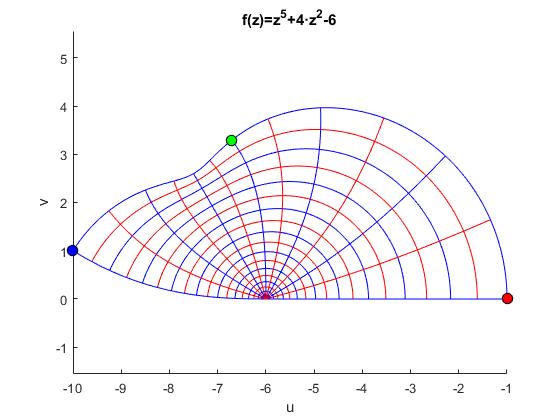
w=z⁵+4z²-6

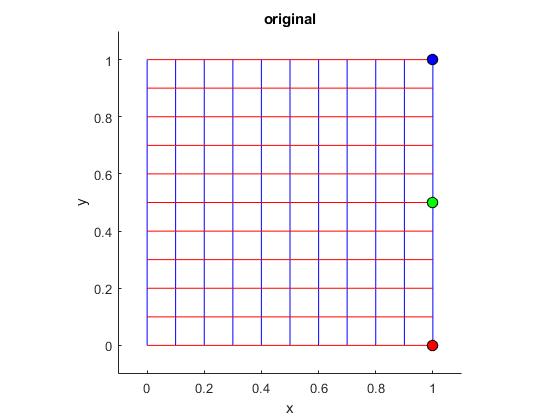
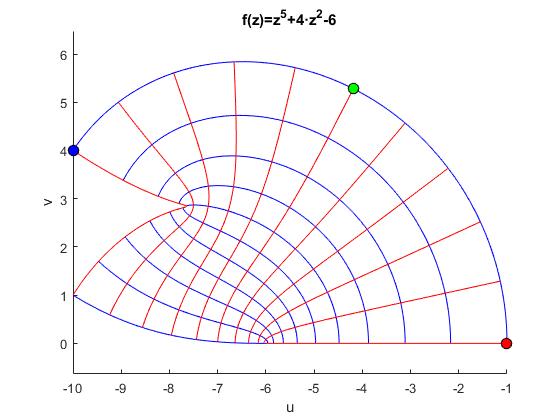
Como ejercicio final de esta página, vamos a explorar la función f(z)=z⁵+4z²-6 y dibujar la región cuadriculada y su imagen mediante f(z).

hold on
for x=0:0.1:1  %líneas verticales
    line([x,x],[0,1],'color','b')
end

for y=0:0.1:1   %líneas horizontales
    line([0,1],[y,y],'color','r');
end

x=[1,1,1];  %tres puntos
y=[0,0.5,1];
color=['r','g','b'];
for k=1:length(x)
    plot(x(k),y(k),'ko','markersize',8,'markerfacecolor',color(k)) 
end
hold off
axis equal
axis([-0.1,1.1,-0.1,1.1])
xlabel('x')
ylabel('y')
title('original')

%transformada
clear
syms x y z;
f=z^5+4*z^2-6;
x=0:0.1:1;
z1=x+1i*y;
ff=subs(f,z,z1);
hold on
for k=1:length(x)
    fplot(real(ff(k)),imag(ff(k)),[0,1],'color','b')
end
clear x;
syms x;
y=0:0.1:1;
z1=x+1i*y;
ff=subs(f,z,z1);
for k=1:length(y)
    fplot(real(ff(k)),imag(ff(k)),[0,1],'color','r');
end
z1=[1,1+1i/2,1+1i];
ff=subs(f,z,z1);
color=['r','g','b'];
for k=1:length(z1)
    plot(real(ff(k)),imag(ff(k)),'ko','markersize',8,'markerfacecolor',color(k)) 
end
hold off
axis equal
xlabel('u')
ylabel('v')
title('f(z)=z^5+4·z^2-6')

hold on
t=(0:2:90)*pi/180; %arcos
for r=0:0.1:1
    plot(r*cos(t),r*sin(t),'b')
end

for r=0.05:0.1:0.95
    plot(r*cos(t),r*sin(t),'r')
end

t=(0:15:90)*pi/180; %líneas radiales
for k=1:length(t)
    line([0,cos(t(k))],[0,sin(t(k))],'color','b');
end

t=(7.5:15:90-7.5)*pi/180; 
for k=1:length(t)
    line([0,cos(t(k))],[0,sin(t(k))],'color','r');
end

t=(0:45:90)*pi/180; %tres puntos
color=['r','g','b'];
for k=1:length(t)
    plot(cos(t(k)),sin(t(k)),'ko','markersize',8,'markerfacecolor',color(k)) 
end
hold off
axis equal
ylim([-0.05,1.05])
xlabel('x')
ylabel('y')
title('original')

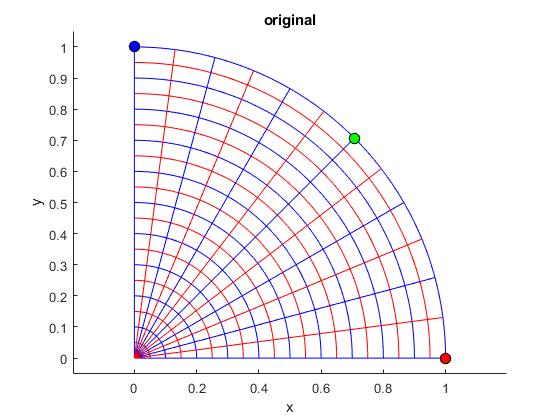
Ahora, la rejilla está formada por arcos de circunferencia y líneas radiales de longitud la unidad, vamos a explorar su transformación bajo la función f(z)=z⁵+4z²-6.

clear
syms t z;
f=z^5+4*z^2-6;

r=0:0.1:1;   %arcos
z1=r*(cos(t)+1i*sin(t));
ff=subs(f,z,z1);
hold on
for k=1:length(r)
    fplot(real(ff(k)),imag(ff(k)),[0,pi/2],'color','b')
end

r=0.05:0.1:0.95;
z1=r*(cos(t)+1i*sin(t));
ff=subs(f,z,z1);
hold on
for k=1:length(r)
    fplot(real(ff(k)),imag(ff(k)),[0,pi/2],'color','r');
end

ang=(0:15:90)*pi/180;  %líneas radiales
z1=(cos(ang)+1i*sin(ang))*t;
ff=subs(f,z,z1);
for k=1:length(ang)
    fplot(real(ff(k)),imag(ff(k)),[0,1],'color','b');  
end
ang=(7.5:15:90-7.5)*pi/180;
z1=(cos(ang)+1i*sin(ang))*t;
ff=subs(f,z,z1);
for k=1:length(ang)
    fplot(real(ff(k)),imag(ff(k)),[0,1],'color','r');
end

z1=[1,cos(pi/4)+1i*sin(pi/4),1i];  %tres puntos
ff=subs(f,z,z1);
color=['r','g','b'];
for k=1:length(z1)
    plot(real(ff(k)),imag(ff(k)),'ko','markersize',8,'markerfacecolor',color(k)) 
end
hold off
axis equal
xlabel('u')
ylabel('v')
title('f(z)=z^5+4·z^2-6')

Referencias

Complex analysis for undergraduate students.

Curvas en el plano complejo

Funciones de variable compleja

Transformada de una recta paralela al eje Y, w=z2

Transformada de una recta paralela al eje Y, w= z

Transformada de una recta paralela al eje Y, w=1/z

Transformada de un segmento de recta, w=iz

Transformada de un arco de circunferencia, w=z2

Transformación lineal

Traslación

Rotación

Ampliación

Transformación lineal

Ejercicio

w=z2

w=z5+4z2-6

Referencias

Transformada de una recta paralela al eje Y, w=z²

Transformada de una recta paralela al eje Y, $w = \sqrt{z}$

Transformada de un arco de circunferencia, w=z²

w=z²

w=z⁵+4z²-6