Rectas y planos

Recta en el espacio (3D)

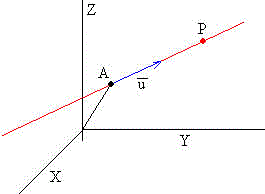
Una recta viene determinada por un punto A (x₀,y₀,z₀) y un vector $\vec{u}$ , cuya dirección es la recta que pasa por los puntos A y P (x,y,z). Llamando $\vec{v}$ al vector de origen A y extremo P, tendremos que

$\vec{v} = t \vec{u} {\begin{cases} x = x_{0} + t u_{x} \\ y = y_{0} + t u_{y} \\ z = z_{0} + t u_{z} \end{cases}$

Considérese la recta r que pasa por el punto A (2,1,3) y tiene por vector director $\vec{u}$ (-1,1,2). Sus ecuaciones paramétricas son

${\begin{cases} x = 2 - t \\ y = 1 + t \\ z = 3 + 2 t \end{cases}$

El punto P(1,2,3) no está en la recta, pues el sistema

${\begin{cases} 2 - t = 1 \\ 1 + t = 2 \\ 3 + 2 t = 3 \end{cases} {\begin{cases} t = 1 \\ t = 1 \\ t = 0 \end{cases}$

es incompatible. En cambio, el punto Q(-1,4,9) si está en la recta

${\begin{cases} 2 - t = - 1 \\ 1 + t = 4 \\ 3 + 2 t = 9 \end{cases} {\begin{cases} t = 3 \\ t = 3 \\ t = 3 \end{cases}$

t=[-0.5,3.5];
hold on
line(2-t,1+t,3+2*t)
plot3(2,1,3,'ro','markersize',4,'markerfacecolor','r');
plot3(1,2,3,'bo','markersize',4,'markerfacecolor','b');
plot3(-1,4,9,'bo','markersize',4,'markerfacecolor','b');
grid on
xlabel('x')
ylabel('y')
zlabel('z')
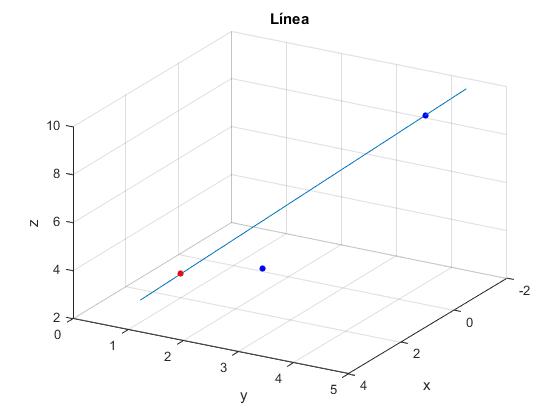
title('Línea')
hold off
view(120,30)

En la figura, vemos el punto A de color rojo, los puntos P y Q de color azul, P no pertenece a la recta y Q si pertenece.

Seleccionado en el menú Tools/Rotate 3D o el icono, señalado en color rojo

con el ratón establecemos distintas vistas view de la figura tridimensional. A medida que actuamos con el puntero del ratón, en la parte inferior izquierda de la ventana, se muestran dos números Az: y El: que corresponden a los parámetros del comando view.

La eliminación del parámetro t da lugar a un sistema de dos ecuaciones lineales independientes

$\frac{x - x_{0}}{u_{x}} = \frac{y - y_{0}}{u_{y}} = \frac{z - z_{0}}{u_{z}}$

Por ejemplo, escribimos las ecuaciones paramétricas de la recta del ejemplo anterior, alternativamente

$\begin{array}{l} 2 - x = y - 1 = \frac{z - 3}{2} \\ {\begin{cases} x + y = 3 \\ 2 x + z = 7 \end{cases} \end{array}$

x=[-1,3];
y=3-x;
z=7-2*x;
line(x,y,z)
grid on
xlabel('x')
ylabel('y')
zlabel('z')
title('Recta')
view(120,30)

Obtenemos un representación gráfica similar de la recta

En general, escribimos la ecuación de la recta

${\begin{cases} a_{1} x + b_{1} y + c_{1} z = d_{1} \\ a_{2} x + b_{2} y + c_{2} z = d_{2} \end{cases} A = (\begin{matrix} a_{1} & b_{1} & c_{1} \\ a_{2} & b_{2} & c_{2} \end{matrix})$

donde el rango de la matriz A es dos. En el ejemplo, anterior

>> A=[1,1,0;2,0,1];
>> rank(A)
ans =     2

Recta que pasa por dos puntos

Hallar la ecuación de la recta que pasa por los puntos, A(2,-1 3) y B(5,0,4),.

A es el punto de coordenadas (x₀,y₀,z₀) y el vector $\vec{u}$ tiene origen en A y extremo en B

x₀=2, y₀=-1; z₀=3, u_x=5-2, u_y=0-(-1),u_z=4-3

${\begin{cases} x = 2 + 3 t \\ y = - 1 + t \\ z = 3 + t \end{cases}$

>> ezplot3('2+3*t','-1+t','3+t',[-1,3]) 
>> view(120,30)

ezplot3 representa en tres dimensiones una función expresada en términos de un parámetro t: x(t), y(t) y z(t) en el intervalo 0<t<2π, por defecto o bien, en el intervalo [t_min,t_max] que se le indique explícitamente.

Plano en el espacio (3D)

Para calcular la ecuación de un plano en el espacio 3D es necesario conocer un punto A (x₀,y₀,z₀) y dos vectores $\vec{u}$ y $\vec{v}$ linealmente independientes. Llamamos $\vec{w}$ al vector de origen A y extremo P (x,y,z)

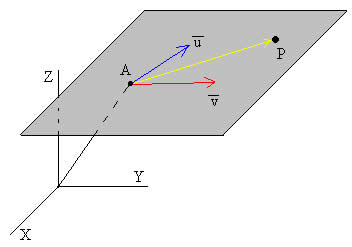
$\vec{w} = t \vec{u} + s \vec{v} {\begin{cases} x = x_{0} + t u_{x} + s v_{x} \\ y = y_{0} + t u_{y} + s v_{y} \\ z = z_{0} + t u_{z} + s v_{z} \end{cases}$

Considérese el plano que pasa por el punto A(2,1,-1) y tiene por vectores directores $\vec{u}$ (1,-1,2) y $\vec{v}$ (-1,2,1). Sus ecuaciones paramétricas son:

${\begin{cases} x = 2 + t - s \\ y = 1 - t + 2 s \\ z = - 1 + 2 t + s \end{cases}$

tt=-0.5:0.1:1.5;
ss=-0.5:0.1:1.5;
hold on
[s,t]=meshgrid(ss,tt);
mesh(2+t-s,1-t+2*s,-1+2*t+s)
plot3(2,1,-1,'ro','markersize',4,'markerfacecolor','r');
plot3(4,3,-2,'bo','markersize',4,'markerfacecolor','b');
plot3(2,2,2,'bo','markersize',4,'markerfacecolor','b');
grid on
xlabel('x')
ylabel('y')
zlabel('z')
title('Plano')
hold off
view(120,30)

El punto P (4,3,-2) no está en el plano, sin embargo, si lo está el punto Q(2,2,2).

Seleccionado en el menú Tools/Data Cursor o el icono, marcado en color rojo

Con el puntero del ratón señalamos un punto en el gráfico tridimensional y se nos proporcionan las coordenadas de dicho punto, tal como vemos en la figura.

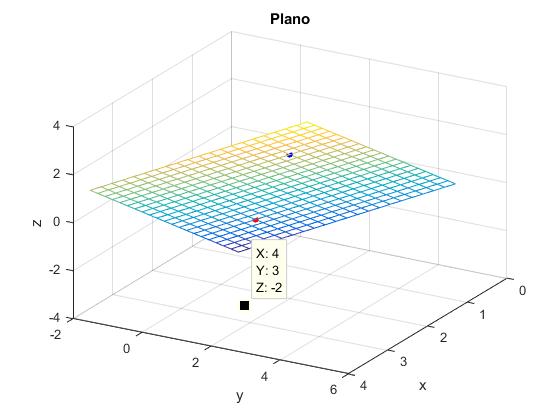
El punto P (4,3,-2) no está en el plano por que el rango de la matriz de los coeficientes que es dos

${\begin{cases} 4 = 2 + t - s \\ 3 = 1 - t + 2 s \\ - 2 = - 1 + 2 t + s \end{cases} {\begin{cases} t - s = 2 \\ - t + 2 s = 2 \\ 2 t + s = - 3 \end{cases}$

por ser $\vec{u}$ y $\vec{v}$ dos vectores linealmente independientes no es igual al rango de la matriz ampliada

>> A=[1,-1;-1,2;2,1];
>> b=[2;2;-3];
>> rank(A)
ans =     2
>> Ab=[A b];
>> rank(Ab)
ans =     3
>> det(Ab)
ans =   -19

En el caso del punto Q (2,2,2)

${\begin{cases} 2 = 2 + t - s \\ 2 = 1 - t + 2 s \\ 2 = - 1 + 2 t + s \end{cases} {\begin{cases} t - s = 0 \\ - t + 2 s = 1 \\ 2 t + s = 3 \end{cases}$

>> A=[1,-1;-1,2;2,1];
>> b=[0;1;3];
>> rank(A)
ans =     2
>> Ab=[A b];
>> rank(Ab)
ans =     2
>> det(Ab)
ans = -1.1102e-015

En general, un punto P(x,y,z) pertenecerá al plano, si el determinante de la matriz ampliada es cero. Obtenemos la ecuación del plano, ax+by+cz+d=0

$\begin{array}{l} {\begin{cases} t u_{x} + s v_{x} = x - x_{0} \\ t u_{y} + s v_{y} = y - y_{0} \\ t u_{z} + s v_{z} = z - z_{0} \end{cases} \\ | \begin{matrix} u_{x} & v_{x} & x - x_{0} \\ u_{y} & v_{y} & y - y_{0} \\ u_{z} & v_{z} & z - z_{0} \end{matrix} | = 0 \\ | \begin{matrix} u_{y} & v_{y} \\ u_{z} & v_{z} \end{matrix} | (x - x_{0}) - | \begin{matrix} u_{x} & v_{x} \\ u_{z} & v_{z} \end{matrix} | (y - y_{0}) + | \begin{matrix} u_{x} & v_{x} \\ u_{y} & v_{y} \end{matrix} | (z - z_{0}) = 0 \\ a (x - x_{0}) + b (y - y_{0}) + c (z - z_{0}) = 0 \\ a x + b y + c z + d = 0 \end{array}$

Hallar la ecuación del plano que pasa por los puntos A(2,1,0), B(1,1,3) y C(0,0,2).

A es el punto de coordenadas (x₀,y₀,z₀), el vector $\vec{u}$ tiene origen en A y extremo en B, el vector $\vec{v}$ tiene origen en A y extremo en C.

x₀=2, y₀=1; z₀=0, u_x=1-2, u_y=1-1,u_z=3-0, v_x=0-2, v_y=0-1,v_z=2-0.

$\begin{array}{l} {\begin{cases} x = 2 - t - 2 s \\ y = 1 - s \\ z = 3 t + 2 s \end{cases} \\ | \begin{matrix} - 1 & - 2 & x - 2 \\ 0 & - 1 & y - 1 \\ 3 & 2 & z \end{matrix} | = 0 \end{array}$

>> syms x y z;
>> A=[-1,-2;0,-1;3,2];
>> b=[x-2;y-1;z];
>> Ab=[A b];
>> det(Ab)
ans =3*x - 4*y + z - 2

La ecuación del plano es 3x-4y+z-2=0

ezmesh representa en tres dimensiones una función expresada en términos de los parámetros t y s: x(t,s), y(t,s) y z(t,s) en el intervalo [t_min,t_max,s_min,s_max].

>> syms t s;
>> ezmesh('2-t-2*s','1-s','3*t+2*s',[-0.5,1.5,-0.5,1.5])
>> view(120,30)

Incidencia y paralelismo

Sean dos planos. Formemos la matriz A y la matriz ampliada Ab

$\begin{array}{l} {\begin{cases} a_{1} x + b_{1} y + c_{1} z = d_{1} \\ a_{2} x + b_{2} y + c_{2} z = d_{2} \end{cases} \\ A = (\begin{matrix} a_{1} & b_{1} & c_{1} \\ a_{2} & b_{2} & c_{2} \end{matrix}) A b = (\begin{matrix} a_{1} & b_{1} & c_{1} & d_{1} \\ a_{2} & b_{2} & c_{2} & d_{2} \end{matrix}) \end{array}$

Planos coincidentes

Dos planos coinciden si el rango de la matriz A y de la matriz Ab valen la unidad

Sean los planos: x-2y+z=1 y -3x+6y-3z=-3

>> A=[1,-2,1;-3,6,-3];
>> b=[1;-3];
>> Ab=[A b];
>> rank(A)
ans =     1
>> rank(Ab)
ans =     1

El segundo plano se obtiene multiplicando el primero por -3, por lo que coinciden

Planos paralelos

Dos planos son paralelos si el rango de la matriz A es uno pero no son coincidentes es decir, el rango de la matriz Ab es dos. Sean los planos: x-2y+z=1 y -2x+4y-2z=6

>> A=[1,-2,1;-2,4,-2];
>> b=[1;6];
>> Ab=[A b];
>> rank(A)
ans =     1
>> rank(Ab)
ans =     2

Representamos los planos

[x,y] = meshgrid(0:0.1:3);
z = 1-x+2*y;
hold on
mesh(x,y,z)
z = 3-x+2*y;
mesh(x,y,z)
xlabel('x')
ylabel('y')
zlabel('z')
title('Planos paralelos')
grid on
hold off
view(120,30)

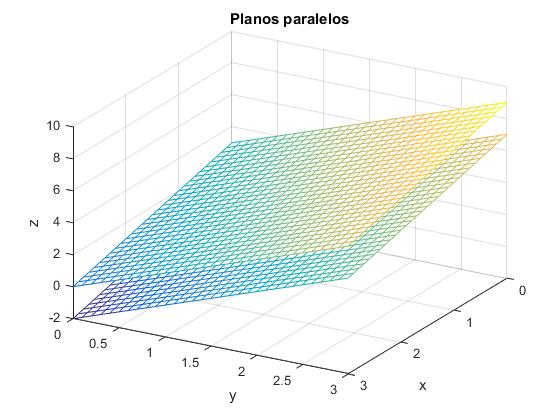
Utilizamos la función ezmesh de MATLAB para hacer una representación similar

>> hold on
>> ezmesh('1-x+2*y',[-1,2,-1,2])
>> ezmesh('3-x+2*y',[-1,2,-1,2])
>> view(120,30)
>> hold off

Planos que se cortan

Sean los planos: x-y+z=2 y 2x-2y+z=1

Para determinar la recta intersección de los dos planos eliminamos z entre las dos ecuaciones, se obtiene y=x+1.

Eliminamos y entre las dos ecuaciones, se obtiene z=3

Se representan los planos y la recta intersección

%dos planos
[x,y] = meshgrid(0:0.1:3);
z = 2-x+y;
hold on
mesh(x,y,z)
z = 1-2*x+2*y;
mesh(x,y,z)
%recta intersección
x=[0,3];
y=x+1;
line(x,y,[3,3], 'color','k')
xlabel('x')
ylabel('y')
zlabel('z')
title('Planos que se cortan')
grid on
hold off
view(120,30)

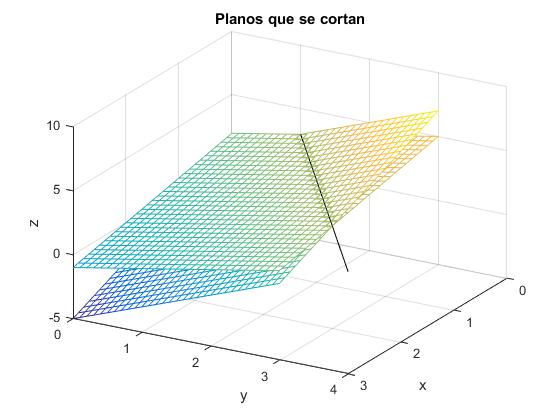
Recta y plano

Sea la recta

${\begin{cases} a_{1} x + b_{1} y + c_{1} z = d_{1} \\ a_{2} x + b_{2} y + c_{2} z = d_{2} \end{cases} A = (\begin{matrix} a_{1} & b_{1} & c_{1} \\ a_{2} & b_{2} & c_{2} \end{matrix})$

donde el rango de la mariz A es dos.

y el plano,

$a_{3} x + b_{3} y + c_{3} z = d_{3}$

La recta y el plano se denominan incidentes si tienen un punto P en común, se tiene que cumplir que

$| \begin{matrix} a_{1} & b_{1} & c_{1} \\ a_{2} & b_{2} & c_{2} \\ a_{3} & b_{3} & c_{3} \end{matrix} | \neq 0$

Sea la recta y el plano

$\begin{array}{l} {\begin{cases} x + y = 1 \\ 2 x - z = 1 \end{cases} \\ x - y + z = 1 \end{array}$

>> A=[1 1,0;2,0,-1]; %recta
>> rank(A)
ans =     2
>> B=[A;[1,-1,1]]; %recta y plano
>> det(B)
ans =    -4
>> b=[1;1;1];
>> X=B\b
X =
    0.7500
    0.2500
    0.5000

Representamos la recta y el plano

%plano
[x,y] = meshgrid(0:0.1:3);
z = 1-x+y;
hold on
mesh(x,y,z)
%recta
mesh(x,y,z)
x=[-1,3];
y=1-x;
z=2*x-1;
line(x,y,z,'color','r')
%punto de intersección
B=[1,1,0;2,0,-1;1,-1,1];
b=[1;1;1];
X=B\b
plot3(X(1),X(2),X(3),'bo','markersize',4,'markerfacecolor','b');
xlabel('x')
ylabel('y')
zlabel('z')
title('Recta que corta a un plano')
grid on
hold off
view(120,30)

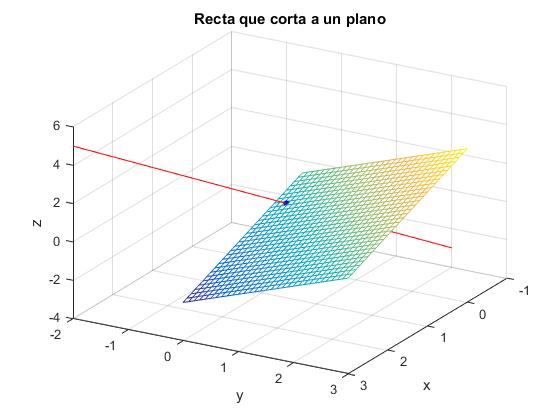
Si la recta y el plano no son incidentes se denominan paralelos y pueden ocurrir los siguientes casos:

Sea la matriz B

$B = (\begin{matrix} a_{1} & b_{1} & c_{1} & d_{1} \\ a_{2} & b_{2} & c_{2} & d_{2} \\ a_{3} & b_{3} & c_{3} & d_{3} \end{matrix})$

Que la recta esté contenida en el plano

El rango de la matriz B será dos

Que la recta no tenga puntos en común con el plano

El rango de la matriz B será tres. El determinante

$| \begin{matrix} a_{1} & b_{1} & c_{1} \\ a_{2} & b_{2} & c_{2} \\ a_{3} & b_{3} & c_{3} \end{matrix} | = 0$

Sea la recta y el plano

$\begin{array}{l} {\begin{cases} 2 x + y + z = 1 \\ x - 2 y + z = - 1 \end{cases} \\ a x + 6 y + 3 z = b \end{array}$

Determinar el valor de a para que el plano sea paralelo a la recta.

>> syms a;
>> C=[2,1,1;1,-2,1;a,6,3];
>> solve(det(C),a)
ans =7

Comprobar que cuando el valor de b=5 el plano contiene a la recta.

El rango de la matriz B tiene que ser dos.

>> B=[2,1,1,1;1,-2,1,-1;7,6,3,5];
>> rank(B)
ans =     2

%plano
[x,y] = meshgrid(-1:0.1:3);
z=(5-7*x-6*y)/3;
mesh(x,y,z)
%recta
mesh(x,y,z)
x=[-1,3];
y=(2-x)/3;
z =(1-5*x)/3;
line(x,y,z,'color','k')
xlabel('x')
ylabel('y')
zlabel('z')
title('Recta paralela a un plano')
grid on
view(120,30)

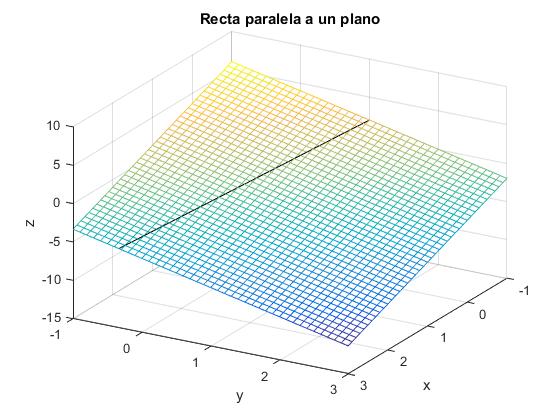
Posiciones relativas de dos rectas

Sean dos rectas r₁ y r₂. Formamos la matriz A de los coeficientes y la matriz Ab ampliada.

$\begin{array}{l} r_{1} {\begin{cases} a_{1} x + b_{1} y + c_{1} z = d_{1} \\ a_{2} x + b_{2} y + c_{2} z = d_{2} \end{cases} \\ r_{2} {\begin{cases} a_{3} x + b_{3} y + c_{3} z = d_{3} \\ a_{4} x + b_{4} y + c_{4} z = d_{4} \end{cases} \\ A = (\begin{matrix} a_{1} & b_{1} & c_{1} \\ a_{2} & b_{2} & c_{2} \\ a_{3} & b_{3} & c_{3} \\ a_{4} & b_{4} & c_{4} \end{matrix}) A b = (\begin{matrix} a_{1} & b_{1} & c_{1} & d_{1} \\ a_{2} & b_{2} & c_{2} & d_{2} \\ a_{3} & b_{3} & c_{3} & d_{3} \\ a_{4} & b_{4} & c_{4} & d_{4} \end{matrix}) \end{array}$

Se pueden producir las situaciones siguientes:

rango Ab\rango A	2	3
2	Coincidentes	Imposible
3	Paralelas. No coincidentes	Secantes
4	Imposible	Se cruzan

Las rectas se cruzan

Sean las rectas r₁ y r₂.

$r_{1} {\begin{cases} x + y + z = 1 \\ 2 x - y + z = 2 \end{cases} r_{2} {\begin{cases} 2 x + y + z = 1 \\ x + y + 2 z = 2 \end{cases}$

Calculamos el rango de la matriz A y de la matriz ampliada Ab

>> A=[1,1,1;2,-1,1;2,1,1;1,1,2];
>> b=[1;2;1;2];
>> Ab=[A b];
>> rank(A)
ans =     3
>> rank(Ab)
ans =     4

Rectas secantes

$r_{1} {\begin{cases} x + y + z = 1 \\ 2 x - y + z = 2 \end{cases} r_{2} {\begin{cases} x + y + z = 1 \\ x + 2 z = 2 \end{cases}$

>> A=[1,1,1;2,-1,1;1,1,1;1,0,2];
>> b=[1;2;1;2];
>> Ab=[A b];
>> rank(A)
ans =     3
>> rank(Ab)
ans =     3

Vemos que la tercera ecuación es idéntica a la primera. Construimos la matriz de los coeficientes de las ecuaciones primera, segunda y cuarta, y el vector de los términos independientes de estas tres ecuaciones. Obtenemos el punto de intersección mediante el operador división por la izquierda.

>> A=[1,1,1;2,-1,1;1,0,2];
>> b=[1;2;2];
>> X=A\b
X =
    0.5000
   -0.2500
    0.7500

Representamos las rectas

x=[-2,2];
%primera recta
y=(x-1)/2;
z=3*(1-x)/2;
hold on
line(x,y,z,'color','r')
%segunda recta
y=-x/2;
z=(2-x)/2;
line(x,y,z,'color','k')
%Punto de intersección 
A=[1,1,1;2,-1,1;1,0,2];
b=[1;2;2];
X=A\b
plot3(X(1),X(2),X(3),'bo','markersize',4,'markerfacecolor','b');
grid on
xlabel('x')
ylabel('y')
zlabel('z')
title('Dos rectas')
hold off
view(120,30)

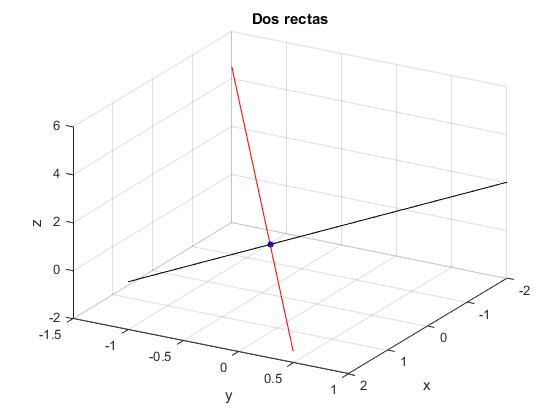
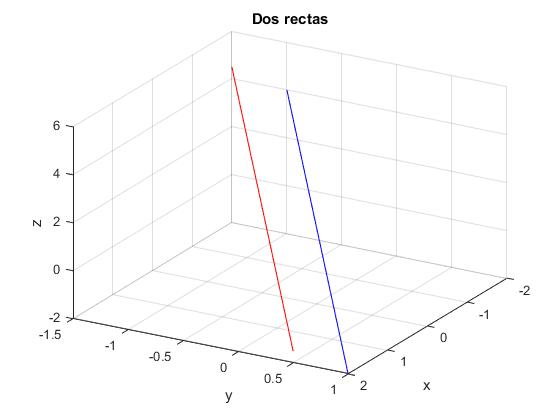
Rectas paralelas

$r_{1} {\begin{cases} x + y + z = 1 \\ 2 x - y + z = 2 \end{cases} r_{2} {\begin{cases} x + y + z = 1 \\ x + 4 y + 2 z = 2 \end{cases}$

>> A=[1,1,1;2,-1,1;1,1,1;1,4,2];
>> b=[1;2;1;2];
>> Ab=[A b];
>> rank(A)
ans =     2
>> rank(Ab)
ans =     3

x=[-2,2];
%primera recta
y=(x-1)/2;
z=3*(1-x)/2;
line(x,y,z,'color','r')
%segunda recta
y=x/2;
z=(2-3*x)/2;
line(x,y,z,'color','b')
grid on
xlabel('x')
ylabel('y')
zlabel('z')
title('Dos rectas')
view(120,30)