Principios de conservación

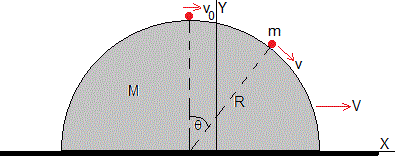
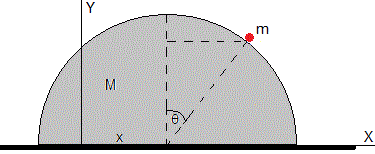
En la figura, observamos una partícula de masa m que se lanza desde el punto más alto θ=0 con velocidad inicial v₀, desliza a lo largo de la cúpula sin rozamiento, en el instante t se ha desplazado θ y lleva una velocidad v

La cúpula de masa M y radio R desliza sobre el plano horizontal sin rozamiento. En el instante inicial t=0 está en reposo y en el instante t lleva una velocidad V

Conservación de la energía

La energía total se mantiene constante e igual a la inicial

${\displaystyle \frac{1}{2}m{v}_0^2+mgR}$

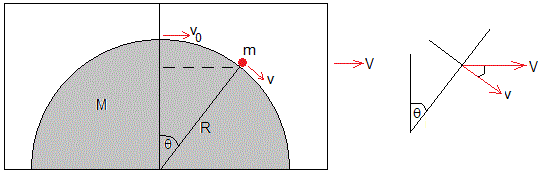
En el instante t, la velocidad de la cúpula es V en la dirección horizontal, la velocidad relativa de la partícula respecto de la cúpula es v=R·dθ/dt, en la dirección tangencial. La velocidad de la partícula es la suma vectorial de estas dos velocidades. Las componentes de la velocidad V en la dirección tangencial y normal son, Vcosθ, Vsinθ, tal como se aprecia en la figura. La energía cinética de la partícula es

${\displaystyle \frac{1}{2}m\left\{{\left(R\frac{d\theta }{dt}+V\cos \theta \right)}^2+V^2{\sin }^2\theta \right\}=\frac{1}{2}m\left(R^2{\left(\frac{d\theta }{dt}\right)}^2+V^2+2VR\frac{d\theta }{dt}\cos \theta \right)}$

La energía potencial de la partícula es mgRcosθ

La energía cinética de la cúpula es MV²/2

Igualamos la energía inicial a la energía del sistema en el instante t

${\displaystyle \begin{array}{l}\frac{1}{2}m{v}_0^2+mgR=\frac{1}{2}m\left(R^2{\left(\frac{d\theta }{dt}\right)}^2+V^2+2VR\frac{d\theta }{dt}\cos \theta \right)+\frac{1}{2}M{V}^2+mgR\cos \theta \\ \frac{1}{2}m{v}_0^2+mgR\left(1-\cos \theta \right)=\frac{1}{2}m{R}^2{\left(\frac{d\theta }{dt}\right)}^2+mVR\frac{d\theta }{dt}\cos \theta +\frac{1}{2}\left(m+M\right)V^2\end{array}}$

Conservación del momento lineal

El peso y la reacción del plano horizontal sobre el que desliza la cúpula son las fuerzas externas que actúan sobre el sistema formado por el cúpula semiesférica y la partícula. No hay fuerzas externas en la dirección horizontal por lo que el momento lineal en esta dirección, se conserva

${\displaystyle m{v}_0=MV+m\left(R\frac{d\theta }{dt}\cos \theta +V\right)}$

R·(dθ/dt)cosθ es la componente horizontal de la velocidad relativa de la partícula. Véase la primera figura

En este sistema de dos ecuaciones eliminamos la velocidad de la cúpula V y despejamos la velocidad relativa R·dθ/dt de la partícula

${\displaystyle \frac{M}{m+M}{v}_0^2+2gR\left(1-\cos \theta \right)=R^2{\left(\frac{d\theta }{dt}\right)}^2\left(1-\frac{m}{m+M}{\cos }^2\theta \right)}$

Ecuaciones del movimiento

Ecuaciones del movimiento de la partícula

Las fuerzas que actúan sobre la partícula son

• el peso mg
• la reacción de la cúpula N, la fuerza que ejerce la cúpula sobre la partícula

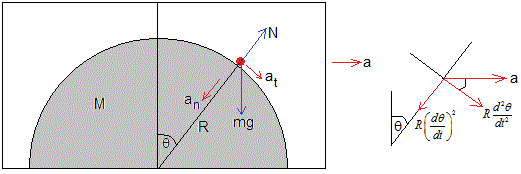
La partícula describe un movimiento circular con aceleraciones relativas

• En la dirección tangencial, $a_t=R\frac{d^2\theta }{d{t}^2}$
• En la dirección normal, $a_n=R{\left(\frac{d\theta }{dt}\right)}^2$

A estas aceleraciones hay que sumarle vectorialmente la aceleración a de la cúpula

• La ecuación del movimiento en la dirección tangencial es

${\displaystyle m\left(R\frac{d^2\theta }{d{t}^2}+a\cos \theta \right)=mg\sin \theta }$

• La ecuación del movimiento en la dirección normal es

${\displaystyle m\left({\left(\frac{d\theta }{dt}\right)}^{2}R-a\sin \theta \right)=mg\cos \theta -N}$

Ecuación del movimiento de la cúpula

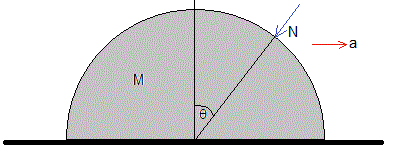
La fuerza que ejerce la partícula sobre la cúpula es N pero de sentido contrario. La ecuación del movimiento de la cúpula es

${\displaystyle Ma=-N\sin \theta }$

Sustituimos N en la segunda ecuación del movimiento de la partícula. En el sistema de dos ecuaciones

${\displaystyle \{\begin{array}{l}R\frac{d^2\theta }{d{t}^2}+a\cos \theta =g\sin \theta \\ m\left({\left(\frac{d\theta }{dt}\right)}^{2}R-a\sin \theta \right)=mg\cos \theta +\frac{Ma}{\sin \theta }\end{array}}$

Eliminamos la aceleración a de la cúpula

${\displaystyle \begin{array}{l}R\frac{d^2\theta }{d{t}^2}+\frac{mR{\left(\frac{d\theta }{dt}\right)}^2-mg\cos \theta }{m\sin \theta +\frac{M}{\sin \theta }}\cos \theta =g\sin \theta \\ \left(m\sin \theta +\frac{M}{\sin \theta }\right)R\frac{d^2\theta }{d{t}^2}+mR{\left(\frac{d\theta }{dt}\right)}^2\cos \theta -mg{\cos }^2\theta =mg{\sin }^2\theta +Mg\\ \left(m{\sin }^2\theta +M\right)R\frac{d^2\theta }{d{t}^2}+mR{\left(\frac{d\theta }{dt}\right)}^2\cos \theta ·\sin \theta -(m+M)g\sin \theta =0\\ \left(m+M-m{\cos }^2\theta \right)R\frac{d^2\theta }{d{t}^2}+mR{\left(\frac{d\theta }{dt}\right)}^2\cos \theta ·\sin \theta -(m+M)g\sin \theta =0\\ \left(1-\frac{m}{m+M}{\cos }^2\theta \right)R\frac{d^2\theta }{d{t}^2}+\frac{m}{m+M}R{\left(\frac{d\theta }{dt}\right)}^2\cos \theta ·\sin \theta -g\sin \theta =0\end{array}}$

Resolveremos esta ecuación del movimiento mediante procedimientos numéricos, sabiendo que en el instante t=0, la partícula parte de la posición θ=0, con velocidad inicial v₀. La partícula permanece en contacto con la cúpula mientras la reacción N>0, hasta un ángulo límite θ_c en el que N=0, que calcularemos en el siguiente apartado

Angulo límite, N=0

Eliminamos la aceleración a de la cúpula en las dos últimas ecuaciones del movimiento (de la partícula y la cúpula) y despejamos la reacción N

${\displaystyle N=\frac{mg\cos \theta -mR{\left(\frac{d\theta }{dt}\right)}^2}{1+\frac{m}{M}{\sin }^2\theta }}$

El ángulo límite θ_c es aquél en el que la partícula deja de estar en contacto con la cúpula, N=0. El numerador es nulo

${\displaystyle R{\left(\frac{d\theta }{dt}\right)}^2=g\cos \theta }$

Del principio de conservación del momento lineal y de la energía, hemos obtenido la velocidad relativa R·dθ/dt de la partícula

${\displaystyle \begin{array}{l}\frac{M}{m+M}{v}_0^2+2gR\left(1-\cos \theta \right)=gR\cos \theta \left(1-\frac{m}{m+M}{\cos }^2\theta \right)\\ \frac{m}{m+M}{\cos }^3\theta -3\cos \theta +2+\frac{M}{m+M}\frac{v_0^2}{gR}=0\\ \frac{\mu }{\mu +1}{\cos }^3\theta -3\cos \theta +2+2\frac{1}{\mu +1}\epsilon =\mathrm{0,}\epsilon =\frac{\frac{1}{2}m{v}_0^2}{mgR},\mu =\frac{m}{M}\end{array}}$

El número adimensional ε es el cociente entre la energía cinética y la potencial inicial en el instante t=0

El ángulo buscado cosθ_c es una de las tres raíces de la ecuación cúbica

El máximo valor de cosθ=1, se alcanza para el valor ε_m=1/2, como se demuestra a continuación

${\displaystyle \begin{array}{l}\frac{\mu }{\mu +1}-3+2+2\frac{1}{\mu +1}{\epsilon }_m=0\\ \frac{-1}{\mu +1}+2\frac{1}{\mu +1}{\epsilon }_m=0\\ \frac{1}{\mu +1}\left(2{\epsilon }_m-1\right)=\mathrm{0,}{\epsilon }_m=\frac{1}{2}\end{array}}$

que es el mismo valor que se obtiene para la cúpula fija. La máxima velocidad inicial es independiente de las masas de la partícula m y de la cúpula M

Cuando la masa de la cúpula es muy grande M→∞, cúpula fija

${\displaystyle \cos {\theta }_c=\frac{2}{3}\left(1+\epsilon \right)=\frac{2}{3}+\frac{1}{3}\frac{v_0^2}{gR}}$

Cuando la velocidad inicial v₀=0, obtenemos cosθ=2/3, θ≈48.2°

Sea una partícula de masa m que desliza sin rozamiento sobre una cúpula de masa M tal que μ=m/M=0.1, la velocidad inicial de la partícula v₀ es tal que ε=1/3. Calculamos las raíces de la ecuación cúbica utilizando la función raices_3. Comprobamos que cosθ_c es la tercera raíz positiva menor que la unidad.

function cupula_1
    m=0.1; %cociente m/M
    epsilon=1/3; %energía adimensional
    p=[m/(1+m),0,-3, 2+2*epsilon/(m+1)]*(1+m)/m; %ecuación tercer grado
    rr=raices_3(p);
    disp(rr) %las tres raíces
    disp(acosd(rr(3))) %ángulo límite

    function x = raices_3(p)
        Q=(p(2)*p(2)-3*p(3))/9;
        R=(2*p(2)^3-9*p(2)*p(3)+27*p(4))/54;
        x=zeros(3,1); %reserva memoria para un vector de tres elementos
        if (R*R)<(Q^3)
            tetha=acos(R/sqrt(Q^3));
            x(1)=-2*sqrt(Q)*cos(tetha/3)-p(2)/3;
            x(2)=-2*sqrt(Q)*cos((tetha+2*pi)/3)-p(2)/3;
            x(3)=-2*sqrt(Q)*cos((tetha-2*pi)/3)-p(2)/3;
        else
            A=-sign(R)*nthroot(abs(R)+sqrt(R*R-Q^3),3);
            if A==0
                B=0;
            else
                B=Q/A;
            end
            x(1)=(A+B)-p(2)/3;
            x(2)=-(A+B)/2-p(2)/3+(sqrt(3)*(A-B)/2)*sqrt(-1); %mejor que i
            x(3)=-(A+B)/2-p(2)/3-(sqrt(3)*(A-B)/2)*sqrt(-1);
        end
    end
end

La tercera raíz es la única válida. El ángulo límite en grados es th_c=acosd(rr(3));, θ_c=27.1200°

   -6.1376
    5.2476
    0.8901

Sea la ecuación cúbica en x=cosθ

${\displaystyle \begin{array}{l}{x}^3+a{x}^2+bx+c=0\\ a=\mathrm{0,}b=-3\frac{\mu +1}{\mu },c=2\frac{\mu +1+\epsilon }{\mu }\\ Q=\frac{\mu +1}{\mu },R=\frac{\mu +1+\epsilon }{\mu }\end{array}}$

Comprobamos que R²<Q³, sabiendo que ε<1/2. La tercera raíz es

${\displaystyle \begin{array}{l}{x}_3=-2\sqrt{Q}\cos \left(\frac{\theta -2\pi }{3}\right)-\frac{a}{3},\theta =\arccos \left(\frac{R}{\sqrt{Q^3}}\right)\\ x_3=-2\sqrt{\frac{\mu +1}{\mu }}\cos \left(\frac{\theta -2\pi }{3}\right),\theta =\arccos \left(\frac{\left(\mu +1+\epsilon \right)\sqrt{\mu }}{\left(\mu +1\right)\sqrt{\mu +1}}\right)\end{array}}$

El código para calcular el ángulo límite se simplifica

m=0.1; %cociente m/M
epsilon=1/3; %energía adimensional
th=acos((m+1+epsilon)*sqrt(m)/((m+1)*sqrt(m+1)));
r3=-2*sqrt((m+1)/m)*cos((th-2*pi)/3);
th_c=acosd(r3);
disp(th_c)

 27.1200

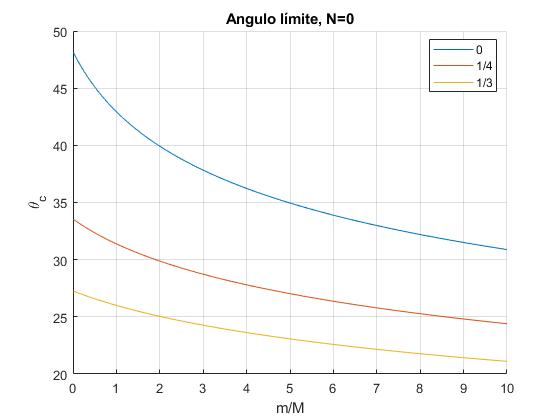
Representamos, el ángulo límite θ_c (en grados) en función de μ=m/M para tres valores de ε=0, 1/4, 1/3

m=linspace(0.01,10,200);
hold on
th_c=zeros(1,length(mm));
for epsilon=[0,1/4,1/3]
    th=acos((m+1+epsilon).*sqrt(m)./((m+1).*sqrt(m+1)));
    r3=-2*sqrt((m+1)./m).*cos((th-2*pi)/3);
    th_c=acosd(r3); %ángulo límite
    plot(m,th_c)
end
hold off
grid on
xlabel('m/M')
legend('0','1/4','1/3','Location','best')
ylabel('\theta_c')
title('Angulo límite, N=0')

Ecuaciones de Lagrange

• Posición

La posición del centro de la cúpula semiesférica y de la partícula respecto del Sistema de Referencia Inercial

${\displaystyle \{\begin{array}{l}\overrightarrow{r_c}=x\widehat{i}\\ \overrightarrow{r_p}=\left(x+R\sin \theta \right)\widehat{i}+R\cos \theta ·\widehat{j}\end{array}}$

• Velocidad

Derivando respecto del tiempo obtenemos el vector velocidad

${\displaystyle \begin{array}{l}\overrightarrow{V}=\frac{dx}{dt}\widehat{i}\\ \overrightarrow{v}=\left(\frac{dx}{dt}+R\cos \theta \frac{d\theta }{dt}\right)\widehat{i}-R\sin \theta \frac{d\theta }{dt}\widehat{j}\end{array}}$

• La energía cinética de la partícula y de la cúpula

${\displaystyle \begin{array}{l}{E}_k=\frac{1}{2}M{\left(\frac{dx}{dt}\right)}^2+\frac{1}{2}m\left\{{\left(\frac{dx}{dt}+R\cos \theta \frac{d\theta }{dt}\right)}^2+{\left(-R\sin \theta \frac{d\theta }{dt}\right)}^2\right\}=\\ \frac{1}{2}(m+M){\left(\frac{dx}{dt}\right)}^2+\frac{1}{2}m{R}^2{\left(\frac{d\theta }{dt}\right)}^2+mR\cos \theta \frac{dx}{dt}\frac{d\theta }{dt}\end{array}}$

• La energía potencial de la partícula

${\displaystyle E_p=mgR\cos \theta }$

La lagrangiana y las ecuaciones del movimiento

${\displaystyle \begin{array}{l}L=E_k-E_p=\frac{1}{2}(m+M){\left(\frac{dx}{dt}\right)}^2+\frac{1}{2}m{R}^2{\left(\frac{d\theta }{dt}\right)}^2+mR\cos \theta \frac{dx}{dt}\frac{d\theta }{dt}-mgR\cos \theta \\ \frac{d}{dt}\left(\frac{\partial L}{\partial \dot{x}}\right)-\frac{\partial L}{\partial x}=0\\ \frac{d}{dt}\left((m+M)\left(\frac{dx}{dt}\right)+mR\cos \theta \frac{d\theta }{dt}\right)=0\end{array}}$

Hay una cantidad que se mantiene constante e igual a su valor inicial, el momento lineal horizontal, mv₀

${\displaystyle (m+M)\left(\frac{dx}{dt}\right)+mR\cos \theta \frac{d\theta }{dt}=m{v}_0}$

La segunda ecuación del movimiento es

${\displaystyle \begin{array}{l}\frac{d}{dt}\left(\frac{\partial L}{\partial \dot{\theta }}\right)-\frac{\partial L}{\partial \theta }=0\\ \frac{d}{dt}\left(R^2\frac{d\theta }{dt}+R\cos \theta \frac{dx}{dt}\right)+R\sin \theta \frac{dx}{dt}\frac{d\theta }{dt}-gR\sin \theta =0\\ R\frac{d^2\theta }{d{t}^2}+\cos \theta \frac{d^{2}x}{d{t}^2}-g\sin \theta =0\end{array}}$

que es la ecuación del movimiento en la dirección tangencial que hemos deducido anteriormente

Derivamos la primera ecuación respecto del tiempo

${\displaystyle (m+M)\frac{d^{2}x}{d{t}^2}+mR\cos \theta \frac{d^2\theta }{d{t}^2}-mR\sin \theta {\left(\frac{d\theta }{dt}\right)}^2=0}$

y con la segunda, eliminamos la aceleración de la cúpula

${\displaystyle R\left(1-\frac{m}{m+M}{\cos }^2\theta \right)\frac{d^2\theta }{d{t}^2}+\frac{m}{m+M}\sin \theta \cos \theta {\left(\frac{d\theta }{dt}\right)}^2-g\sin \theta =0}$

Obteniendo la misma ecuación diferencial que aplicando la Segunda Ley de Newton

Movimiento de los cuerpos

En este apartado describimos las distintas etapas del movimiento de la cúpula y la partícula

Movimiento relativo de la partícula

Resolvemos la ecuación diferencial por el procedimiento ode45 de MATLAB para una cúpula de radio R=1 m. El cociente de m/M=0.2, entre la masa de la partícula y de la cúpula. La partícula parte de la posición θ=0, más alta, con velocidad inicial dada por el parámetrro adimensional ε=1/10

${\displaystyle \epsilon =\frac{m{v}_0^2}{2mgR},{\left(\frac{d\theta }{dt}\right)}_{t=0}=\frac{v_0}{R}=\sqrt{2\epsilon \frac{g}{R}}}$

Representamos la posición de la partícula θ que desliza sobre la cúpula mientras están en contacto N>0. Marcamos con un punto de color rojo, la posición final N=0.

function cupula_3    
    R=1; %radio
    m=0.2; %cociente m/M
    epsilon=1/10; %energía adimensional
    th=acos((m+1+epsilon)*sqrt(m)/((m+1)*sqrt(m+1)));
    r3=-2*sqrt((m+1)/m)*cos((th-2*pi)/3);
    th_c=acos(r3); %ángulo límite
    disp(th_c*180/pi)
    
    v0=sqrt(2*epsilon*9.8*R); %velocidad inicial
    f=@(t,x) [x(2);(9.8*sin(x(1))-m*sin(x(1))*cos(x(1))*x(2)^2/(m+1))/
(R*(1-m*cos(x(1))^2/(m+1)))]; 
    opts=odeset('events',@(t,x) stop_cupula(t,x,th_c));
    [t,x]=ode45(f,[0,100],[0,v0/R],opts);
    %conservación de la energía, velocidad relativa final de la partícula
    v=sqrt((v0^2/(1+m)+2*9.8*R*(1-cos(th_c)))/(1-cos(th_c)^2*m/(1+m))); 
    disp([v,x(end,2)]) 
    disp(t(end)) %tiempo final
    hold on
    plot(t,x(:,1)*180/pi)
    plot(t(end),x(end,1)*180/pi,'ro','markersize',3,'markerfacecolor','r')
    line([t(end),t(end)],[0,x(end,1)*180/pi],'lineStyle','--')
    line([0,t(end)],[x(end,1)*180/pi,x(end,1)*180/pi],'lineStyle','--')
    hold off
    grid on
    xlabel('t')
    ylabel('\theta')
    title('Cúpula semiesférica móvil')
%añadir aquí el código para representar la posición y velocidad de la cúpula

    function [value,isterminal,direction]=stop_cupula(~,x,xFin)
        value=x(1)-xFin; 
        isterminal=1;
        direction=1; 
    end
end

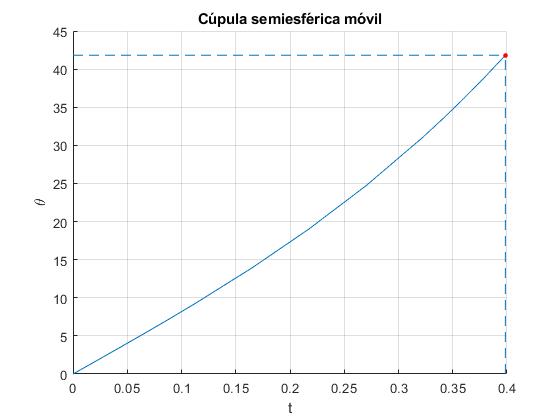
El ángulo límite es θ_c=41.8° la posición angular final de la partícula sobre la cúpula se alcanza en el instante t_c=0.3985 s. Comprobamos que el procedimiento numérico ode45 produce buenos resultados comparando la velocidad relativa final de la partícula x(end,2)=2.7031 con la que se obtiene aplicando el principio de conservación de la energía, v=2.7024

   41.8225
    2.7024    2.7031
    0.3985

Movimiento de la cúpula

No es necesario resolver la ecuación diferencial en x para calcular la posición del centro de la cúpula. La conservación del momento lineal en la dirección horizontal es equivalente a decir que el centro de masas se mueve con velcidad constante igual a la velocidad inicial. La posición inicial del centro de masas es el origen, x=0, θ=0

${\displaystyle \begin{array}{l}{x}_{cm}=\frac{Mx+m\left(x+R\sin \theta \right)}{m+M}\\ v_{cm}=\frac{m{v}_0}{m+M}\\ x_{cm}=v_{cm}t\end{array}}$

Despejamos x, la posición del centro de la cúpula

${\displaystyle x=\frac{m}{m+M}\left(v_{0}t-R\sin \theta \right)}$

Añadimos esta porción de código, para representar la posición del centro de la cúpula x en función del tiempo

De modo similar, la velocidad de la cúpula es

...
     figure
     xc=m*(v0*t-R*sin(x(:,1)))/(1+m);
     plot(t,xc)
     grid on
     xlabel('t')
     ylabel('x')
     title('Cúpula semiesférica móvil')

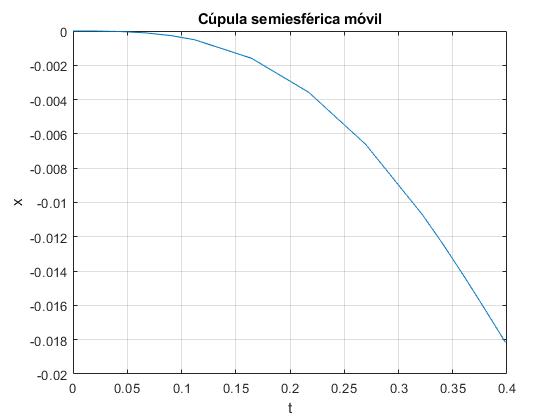
La cúpula se mueve hacia la izquierda, alrededor de 1.8 cm

De modo similar, la velocidad de la cúpula es

${\displaystyle \begin{array}{l}{v}_{cm}=\frac{MV+m\left(R\frac{d\theta }{dt}\cos \theta +V\right)}{m+M}=\frac{m{v}_0}{m+M}\\ V=\frac{m}{m+M}\left(v_0-R\frac{d\theta }{dt}\cos \theta \right)\end{array}}$

Añadimos esta porción de código, para representar la velocidad del centro de la cúpula V en función del tiempo

...
     figure
     V=m*(v0-R*cos(x(:,1)).*x(:,2))/(1+m);
     plot(t,V)
     grid on
     xlabel('t')
     ylabel('V')
     title('Cúpula semiesférica móvil')

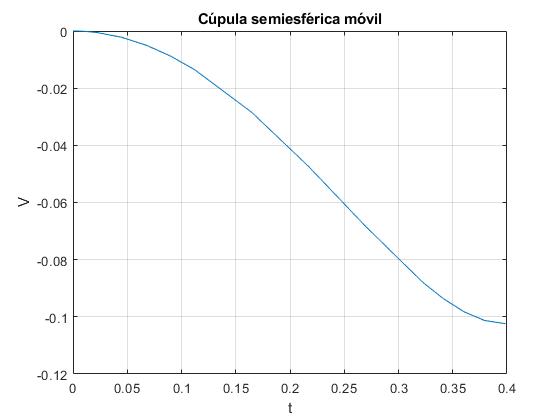
La velocidad final de la cúpula es de alrededor de 10 cm/s hacia la izquierda

Cuando la partícula deja de estar en contacto con la cúpula, describe un movimiento parabólico, tal como se explica en la página titulada Movimiento sobre una cúpula semiesférica. La cúpula sigue un movimiento rectilíneo con velocidad constante

Movimiento bajo la aceleración constante de la gravedad

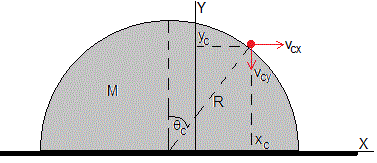
La trayectoria parabólica comienza cuando la reacción N=0, la posición relativa de la partícula es el ángulo límite θ_c habiendo empleando un tiempo t_c en alcanzarla.

Para describir el movimiento bajo la acción constante de la gravedad precisamos de la posición inicial (x_c, y_c) y de la velocidad inicial (v_cx, v_cy)

${\displaystyle \{\begin{array}{l}{x}_c=\frac{m}{m+M}\left(v_0{t}_c-R\sin {\theta }_c\right)+R\sin {\theta }_c=\frac{m}{m+M}{v}_0{t}_c+\frac{M}{m+M}R\sin {\theta }_c\\ y_c=R\cos {\theta }_c\end{array}}$

Aplicando el principio de conservación de la energía, calculamos el módulo de la velocidad relativa de la partícula R·(dθ/dt)_c en el instante t_c

${\displaystyle \frac{M}{m+M}{v}_0^2+2gR\left(1-\cos {\theta }_c\right)=R^2{\left(\frac{d\theta }{dt}\right)}_c^2\left(1-\frac{m}{m+M}{\cos }^2{\theta }_c\right)}$

Las componentes de la velocidad inicial son

${\displaystyle \{\begin{array}{l}{v}_{cx}=V+R\frac{d\theta }{dt}\cos \theta =\frac{m}{m+M}{v}_0+\frac{M}{m+M}R{\left(\frac{d\theta }{dt}\right)}_c\cos {\theta }_c\\ v_{cy}=-R{\left(\frac{d\theta }{dt}\right)}_c\sin {\theta }_c\end{array}}$

La ecuación de la trayectoria, es

${\displaystyle \{\begin{array}{l}x=x_c+v_{cx}t\\ y=y_c+v_{cy}t-\frac{1}{2}g{t}^2\end{array}}$

Se empieza a contar el tiempo cuando la partícula sale de la cúpula. La partícula impacta en el plano horizontal y=0, en el instante t_f.

Actividades

Se introduce

• El cociente de las masas m/M de la partícula y la masa de la cúpula, en el control titulado Cociente masas
• La energía adimensional ε<1/2, en el control titulado Energía

Se pulsa el botón titulado Nuevo

Cuando la energía ε=0, la velocidad inicial v₀=0, la partícula permence en la posición de equilibrio inestable θ=0. El programa interactivo sustituye ε=0 por ε=0.0001. Del mismo modo, sustituye ε=0.5 (el ángulo límite, θ_c=0), por ε=0.49

En la parte superior derecha, se proporcionan los siguientes datos

• El tiempo t
• la posición angular θ de la partícula
• la reacción N en unidades del peso, mg
• la posición del centro de la cúpula en cm
• la velocidad de la cúpula en cm/s

Referencias

Roberto A Lineros. Sliding down over a horizontally moving semi-sphere. Eur. J. Phys. 43 (2022) 035004