El ciclo de Carnot

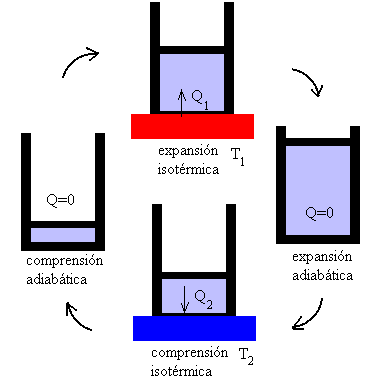
Gas ideal

La representación gráfica del ciclo de Carnot en un diagrama p-V es el siguiente

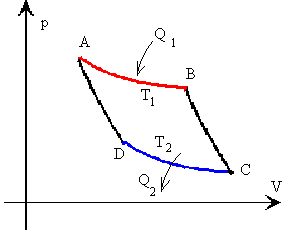
Tramo A-B isoterma a la temperatura T₁
Tramo B-C adiabática
Tramo C-D isoterma a la temperatura T₂
Tramo D-A adiabática

En cualquier ciclo, tenemos que obtener a partir de los datos iniciales:

La presión, volumen de cada uno de los vértices.
El trabajo, el calor y la variación de energía interna en cada una de los procesos.
El trabajo total, el calor absorbido, el calor cedido y el rendimiento del ciclo.

Los datos iniciales son los que figuran en la tabla adjunta. A partir de estos datos, hemos de rellenar los huecos de la tabla.

Variables	A	B	C	D
Presión p (atm)	p_A
Volumen V (litros)	V_A	V_B
Temperatura T (K)	T₁	T₁	T₂	T₂

Las etapas del ciclo

Para obtener las variables y magnitudes desconocidas emplearemos las fórmulas que figuran en el cuadro-resumen de las transformaciones termodinámicas.

Transformación A->B (isoterma)

La presión p_B se calcula a partir de la ecuación del gas ideal $p_{B} V_{B} = n R T_{1}$

Variación de energía interna $Δ U_{A \to B} = 0$

Trabajo $W_{A \to B} = n R T_{1} \ln \frac{V_{B}}{V_{A}}$

Calor $Q_{A \to B} = W_{A \to B}$

Transformación B->C (adiabática)

La ecuación de estado adiabática es $p V^{γ} = cte$ o bien, $T V^{γ - 1} = cte$ . Se despeja V_c de la ecuación de la adiabática $T_{1} V_{B}^{γ - 1} = T_{2} V_{C}^{γ - 1}$ . Conocido V_c y T₂ se obtiene p_c, a partir de la ecuación del gas ideal, $p_{C} V_{C} = n R T_{2}$ .

Calor $Q_{B \to C} = 0$

Variación de energía interna $Δ U_{B \to C} = n c_{v} (T_{2} - T_{1})$

Trabajo $W_{B \to C} = - Δ U_{B \to C}$

Transformación C->D (isoterma)

Variación de energía interna $Δ U_{C \to D} = 0$

Trabajo $W_{C \to D} = n R T_{2} \ln \frac{V_{D}}{V_{C}}$

Calor $Q_{C \to D} = W_{C \to D}$

Transformación D-> A (adiabática)

Se despeja V_Dde la ecuación de la adiabática $T_{1} V_{A}^{γ - 1} = T_{2} V_{D}^{γ - 1}$ . Conocido V_D y T₂ se obtiene p_D, a partir de la ecuación del gas ideal, $p_{D} V_{D} = n R T_{2}$ .

Calor $Q_{D \to A} = 0$

Variación de energía interna $Δ U_{D \to A} = n c_{v} (T_{1} - T_{2})$

Trabajo $W_{D \to A} = - Δ U_{D \to A}$

A partir de las ecuaciones de las dos adiabáticas, probamos que la relación entre los volúmenes de los vértices es

$\frac{V_{B}}{V_{A}} = \frac{V_{C}}{V_{D}}$

El ciclo completo

Variación de energía interna

$Δ U = Δ U_{B \to C} + Δ U_{D \to A} = 0$

En un proceso cíclico reversible la variación de energía interna es cero

Trabajo

$W = W_{A \to B} + W_{B \to C} + W_{C \to D} + W_{D \to A} = n R (T_{1} - T_{2}) \ln \frac{V_{B}}{V_{A}}$

Calor

En la isoterma T₁ se absorbe calor Q>0 ya que V_B>V_A de modo que $Q_{a b s} = n R T_{1} \ln \frac{V_{B}}{V_{A}}$

En la isoterma T₂ se cede calor Q<0 ya que V_D<V_C

Rendimiento del ciclo

Se define rendimiento como el cociente entre el trabajo realizado y el calor absorbido

$η = \frac{W}{Q_{a b s}} = 1 - \frac{T_{2}}{T_{1}}$

Ejemplo

Un gas monoatómico, c_v=3R/2, describe el ciclo de Carnot de la figura. Las transformaciones A-B y C-D son isotermas a la temperatura T₁=450 K y T₂=293 K. Las transformaciones B-C y D-A son adiabáticas. Se conoce la presión p_A=15 atm, el volumen v_A=4 l, y el volumen v_B=8 l (Véase la figura al final de la página)

Hallar los valores de la presión, el volumen, y la temperatura de cada uno de los vértices A, B, C y D a partir de los datos suministrados.
Calcular de forma explícita el trabajo en cada una de las transformaciones, la variación de energía interna y el calor.
Hallar el rendimiento del ciclo y comprobar que coincide con el valor dado por la fórmula del rendimiento de un ciclo de Carnot.

Dato: R=8.314 J/(K mol)=0.082 atm.l/(K mol)

Presión y volumen de los cuatro vértices

$\begin{array}{l} c_{p} = c_{v} + R = \frac{3}{2} R + R = \frac{5}{2} R γ = \frac{c_{p}}{c_{v}} = \frac{5}{3} \\ p V = n R T 15 \cdot 4 = n R \cdot 450 n R = \frac{2}{15} \\ A \to B (isoterma) 15 \cdot 4 = p_{B} \cdot 8 p_{B} = 7.5 atm T_{A} = T_{B} = 450 K \\ B \to C (adiabática) {\begin{cases} T_{B} V_{B}^{γ - 1} = T_{C} V_{C}^{γ - 1} 450 \cdot 8^{2 / 3} = 293 \cdot V_{C}^{2 / 3} V_{C} = 15.23 l \\ P_{C} V_{C} = n R T_{C} P_{C} \cdot 15.23 = \frac{2}{15} 293 P_{C} = 2.57 atm \end{cases} \\ C \to D (isoterma) T_{C} = T_{D} = 293 K \\ D \to A (adiabática) {\begin{cases} T_{A} V_{A}^{γ - 1} = T_{D} V_{D}^{γ - 1} 450 \cdot 4^{2 / 3} = 293 \cdot V_{D}^{2 / 3} V_{D} = 7.61 l \\ P_{D} V_{D} = n R T_{D} P_{D} \cdot 7.61 = \frac{2}{15} 293 P_{D} = 5.13 atm \end{cases} \end{array}$

Vértice	p(atm)	V(l)	T(K)
A	15	4	450
B	7.5	8	450
C	2.57	15.23	293
D	5.13	7.61	293

Trabajo, calor y variación de energía interna en los cuatro procesos

$\begin{array}{l} A \to B (isoterma) \\ Δ U_{A B} = 0 \\ Q_{A B} = W_{A B} = n R T_{B} \ln \frac{V_{B}}{V_{A}} = \frac{2}{15} 450 \ln \frac{8}{4} = 41.59 atm·l \\ C \to D (isoterma) \\ Δ U_{C D} = 0 \\ Q_{C D} = W_{C D} = n R T_{D} \ln \frac{V_{D}}{V_{C}} = \frac{2}{15} 293 \ln \frac{7.61}{15.23} = - 27.08 atm·l \\ B \to C (adiabática) \\ Δ U_{B C} = n c_{v} (T_{C} - T_{B}) = n \frac{3}{2} R (310 - 850) = \frac{2}{15} \frac{3}{2} (293 - 450) = - 31.40 atm·l \\ Q_{B C} = 0 \\ W_{B C} = 31.40 atm·l \\ D \to A (adiabática) \\ Δ U_{D A} = n c_{v} (T_{C} - T_{B}) = n \frac{3}{2} R (450 - 293) = \frac{2}{15} \frac{3}{2} (450 - 293) = 31.40 atm·l \\ Q_{D A} = 0 \end{array}$

Proceso	W(atm·l)	Q(atm·l)	ΔU(atm·l)
A→B	41.59	41.59	0
B→C	31.40	0	-31.40
C→D	-27.08	-27.08	0
D→A	-31.40	0	31.40
Ciclo	14.51		0

Ciclo completo

Trabajo total: W=14.51 atm·l
Calor absorbido: Q_abs=41.59 atm·l
Calor cedido: Q_ced=27.08 atm·l

Rendimiento

$\begin{array}{l} η = \frac{W}{Q_{a b s}} = \frac{14.51}{41.59} = 0.349 \\ η = 1 - \frac{T_{A B}}{T_{C D}} = 1 - \frac{293}{450} = 0.349 \end{array}$

Elaboramos un script para calcular la presión, volumen y temperatura de los cuatro vértices cuando se conoce:

La temperatura T₁ de la isoterma que pasa por A y B
La temperatura T₂ de la isoterma que pasa por C y D (T₂<T₁)
La presión p_A y el volumen v_A
El volumen v_B (v_B>v_A)
Si el gas ideal es monoatómico o diatómico

El programa, calcula el trabajo y calor en cada etapa del ciclo.

El trabajo total, el calor absorbido, el calor cedido y el redimiento del ciclo

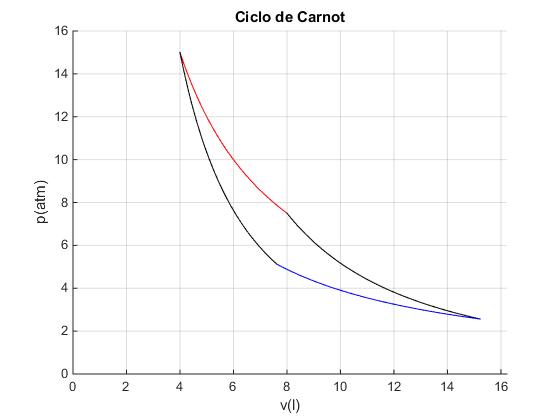
La representación gráfica del ciclo

Este script puede servir de modelo para resolver cualquier otro ciclo

%datos
T1=450;  % Temperatura de la isoterma A y B 
T2=293;  %temperatura de la isoterma C y D
vA=4;  
vB=8;
pA=15;
R=0.082; %constante de los gases (atm·l)/(K·mol)
%gas monoatómico
gamma=5/3; % 7/5 para el diatómico
cV=3*R/2;  %calor específico, 5*R/2 para el diatómico

%resultados
nMoles=pA*vA/(R*T1);
disp('Vértices');

pB=pA*vA/vB;
vC=(T1*vB^(gamma-1)/T2)^(1/(gamma-1));
pC=nMoles*R*T2/vC;
vD=(T1*vA^(gamma-1)/T2)^(1/(gamma-1));
pD=nMoles*R*T2/vD;
fprintf('Vertice A: pA=%2.2f, vA=%2.2f, TA=%2.2f\n', pA, vA, T1)
fprintf('Vertice B: pB=%2.2f, vB=%2.2f, TB=%2.2f\n', pB, vB, T1)
fprintf('Vertice C: pC=%2.2f, vC=%2.2f, TC=%2.2f\n', pC, vC, T2)
fprintf('Vertice D: pD=%2.2f, vD=%2.2f, TD=%2.2f\n', pD, vD, T2)

disp('Trabajo');
W_AB=nMoles*R*T1*log(vB/vA);
W_BC=nMoles*cV*(T1-T2);
W_CD=nMoles*R*T2*log(vD/vC);
W_DA=nMoles*cV*(T2-T1);
fprintf('W_AB=%2.2f, W_BC=%2.2f, W_CD=%2.2f, W_DA=%2.2f\n',
 W_AB, W_BC, W_CD, W_DA)

disp('Calor');
Q_AB=W_AB;
Q_BC=0;
Q_CD=W_CD;
Q_DA=0;
fprintf('Q_AB=%2.2f, Q_BC=%2.2f, Q_CD=%2.2f, Q_DA=%2.2f\n'
, Q_AB, Q_BC, Q_CD, Q_DA)

disp('Total')
W=W_AB+W_BC+W_CD+W_DA;
Q=Q_AB+Q_BC+Q_CD+Q_DA;
fprintf('Trabajo=%2.2f, Calor absorbido=%2.2f, Calor cedido=%2.2f,
rendimiento=%1.2f\n', W, Q_AB, Q_CD, W/Q_AB);
rendimiento=1-T2/T1;
disp(rendimiento)

%gráfica del ciclo
hold on
fplot(@(v) v,@(v) (nMoles*R*T1)./v, [vA,vB], 'r')
fplot(@(v) v,@(v) (pB*vB^gamma)./v.^gamma,[vB,vC], 'k')
fplot(@(v) v,@(v) (nMoles*R*T2)./v, [vD,vC],'b')
fplot(@(v) v,@(v) (pA*vA^gamma)./v.^gamma,[vA,vD],'k')

xlim([0,vC+1])
ylim([0,pA+1])
hold off
grid on
xlabel('v(l)')
ylabel('p(atm)')
title('Ciclo de Carnot')

Vértices
Vertice A: pA=15.00, vA=4.00, TA=450.00
Vertice B: pB=7.50, vB=8.00, TB=450.00
Vertice C: pC=2.57, vC=15.23, TC=293.00
Vertice D: pD=5.13, vD=7.61, TD=293.00
Trabajo
W_AB=41.59, W_BC=31.40, W_CD=-27.08, W_DA=-31.40
Calor
Q_AB=41.59, Q_BC=0.00, Q_CD=-27.08, Q_DA=0.00
Total
Trabajo=14.51, Calor absorbido=41.59, Calor cedido=-27.08, rendimiento=0.35

rendimiento =    0.3489

Gas de van der Waals

La ecuación de van der Waals tiene en cuenta el volumen finito de las moléculas y las fuerzas atractivas que una molécula ejerce sobre otra a distancias muy cercanas entre ellas.

$(p + \frac{n^{2} a}{V^{2}}) (V - n b) = n R T$

Las constantes a y b son característicos de cada gas y se obtienen a partir de los datos de la presión P_c, volumen V_c y la temperatura T_c crítica.

Transformación adiabática

La entropía de una sustancia es una función de dos variables, la temperatura T y el volumen V. La tercera variable p está relacionada con las otras dos V y T por la ecuación de estado

$\begin{array}{l} S = S (T, V) \\ d S = {(\frac{\partial S}{\partial T})}_{V} d T + {(\frac{\partial S}{\partial V})}_{T} d V \\ T d S = T {(\frac{\partial S}{\partial T})}_{V} d T + T {(\frac{\partial S}{\partial V})}_{T} d V \end{array}$

Hemos multiplicado ambos miembros por la temperatura T

Teniendo en cuenta δQ=T·dS, y δQ=nc_vdT, en una transformación a volumen constante

$\begin{array}{l} n c_{v} d T = T {(\frac{\partial S}{\partial T})}_{V} d T \\ n c_{v} = T {(\frac{\partial S}{\partial T})}_{V} \end{array}$

donde c_v es el calor específico a volumen constante.

$T d S = n c_{v} d T + T {(\frac{\partial S}{\partial V})}_{T} d V$

Teniendo en cuenta la tercera relación de Maxwell

${(\frac{\partial S}{\partial V})}_{T} = {(\frac{\partial p}{\partial T})}_{V}$

obtenemos

$T d S = n c_{v} d T + T {(\frac{\partial p}{\partial T})}_{V} d V$

En una transformación adiabática, δQ=T·dS=0

$n c_{v} d T + T {(\frac{\partial p}{\partial T})}_{V} d V = 0$

Para el gas de van der Waals

$\begin{array}{l} p = \frac{n R T}{V - n b} - \frac{n^{2} a}{V^{2}} \\ {(\frac{\partial p}{\partial T})}_{V} = \frac{n R}{V - n b} \end{array}$

Obtenemos

$n c_{v} d T + T \frac{n R}{V - n b} d V = 0$

Separamos variables e integramos

$\begin{array}{l} c_{v} \frac{d T}{T} = - \frac{R}{V - n b} d V \\ c_{v} \ln T = - R \ln (V - n b) + C \\ \ln T + \ln {(V - n b)}^{\frac{R}{c_{v}}} = C \\ T {(V - n b)}^{\frac{R}{c_{v}}} = C \end{array}$

Despejamos la temperatura T en la ecuación de van der Waals y la introducimos en esta última ecuación

$\begin{array}{l} T = \frac{1}{n R} (p + \frac{n^{2} a}{V^{2}}) (V - n b) \\ \frac{1}{n R} (p + \frac{n^{2} a}{V^{2}}) (V - n b) {(V - n b)}^{\frac{R}{c_{v}}} = C \\ (p + \frac{n^{2} a}{V^{2}}) {(V - n b)}^{Γ} = C, Γ = \frac{R}{c_{v}} + 1 \end{array}$

El índice Γ es distinto de γ=c_p/c_v de un proceso adiabático con gas ideal. C es una constante

Calor específico a volumen connstante c_v

Aplicamos el primer pricipio de la Termodinámica

$\begin{array}{l} δ Q = T d S = n c_{v} d T + T {(\frac{\partial p}{\partial T})}_{V} d V \\ d U = δ Q - p d V = n c_{v} d T + (T {(\frac{\partial p}{\partial T})}_{V} - p) d V \end{array}$

Para que dU sea diferencial exacta, se tiene que cumplir que

$\begin{array}{l} d U (t, x) = P (t, x) d t + Q (t, x) d x \\ \frac{\partial P}{\partial x} = \frac{\partial Q}{\partial t} \end{array}$

En nuestro caso

$\begin{array}{l} n \frac{\partial c_{v}}{\partial V} = \frac{\partial}{\partial T} (T {(\frac{\partial p}{\partial T})}_{V} - p) \\ n \frac{\partial c_{v}}{\partial V} = \frac{\partial}{\partial T} (T \frac{n R}{V - n b} - \frac{n R T}{V - n b} + \frac{n^{2} a}{V^{2}}) \\ \frac{\partial c_{v}}{\partial V} = \frac{\partial}{\partial T} (\frac{n a}{V^{2}}) \\ \frac{\partial c_{v}}{\partial V} = 0 \end{array}$

Lo que indica que el calor específico c_v no depende del volumen V, solamente de la temperatura T.

Calor

Partiendo de la ecuación

$δ Q = n c_{v} d T + T {(\frac{\partial p}{\partial T})}_{V} d V$

Para el gas de van der Waals

$δ Q = n c_{v} d T + T \frac{n R}{V - n b} d V$

Si la temperatura es constante

$δ Q = T \frac{n R}{V - n b} d V$

Trabajo y calor en las cuatro transformaciones

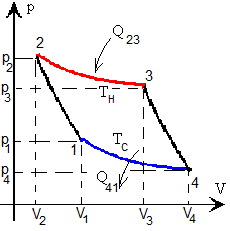
Transformación 1--->2, el gas se comprime adiabáticamente entre V₁ y V₂

Por ser transformación adiabática se cumple

$(p_{1} + \frac{n^{2} a}{V_{1}^{2}}) {(V_{1} - n b)}^{Γ} = (p + \frac{n^{2} a}{V^{2}}) {(V - n b)}^{Γ} = (p_{2} + \frac{n^{2} a}{V_{2}^{2}}) {(V_{2} - n b)}^{Γ} = C$

El trabajo W₁₂ es

$\begin{array}{l} W_{12} = \int_{V_{1}}^{V_{2}} p d V = \int_{V_{1}}^{V_{2}} (\frac{C}{{(V - n b)}^{Γ}} - \frac{n^{2} a}{V^{2}}) d V = \frac{C}{- Γ + 1} ({(V_{2} - n b)}^{- Γ + 1} - {(V_{1} - n b)}^{- Γ + 1}) + \frac{n^{2} a}{V_{2}} - \frac{n^{2} a}{V_{1}} = \\ \frac{1}{- Γ + 1} ((p_{2} + \frac{n^{2} a}{V_{2}^{2}}) {(V_{2} - n b)}^{Γ} {(V_{2} - n b)}^{- Γ + 1} - (p_{1} + \frac{n^{2} a}{V_{1}^{2}}) {(V_{1} - n b)}^{Γ} {(V_{1} - n b)}^{- Γ + 1}) + \frac{n^{2} a}{V_{2}} - \frac{n^{2} a}{V_{1}} = \\ - \frac{c_{v}}{R} ((p_{2} + \frac{n^{2} a}{V_{2}^{2}}) (V_{2} - n b) - (p_{1} + \frac{n^{2} a}{V_{1}^{2}}) (V_{1} - n b)) + \frac{n^{2} a}{V_{2}} - \frac{n^{2} a}{V_{1}} = - n c_{v} (T_{H} - T_{C}) + \frac{n^{2} a}{V_{2}} - \frac{n^{2} a}{V_{1}} \end{array}$

El calor Q₁₂=0

$\begin{array}{l} δ Q = n c_{v} d T + T \frac{n R}{V - n b} d V = 0 \\ \int_{T_{C}}^{T_{H}} c_{v} \frac{d T}{T} + R \int_{V_{1}}^{V_{2}} \frac{d V}{V - n b} = 0 \\ \int_{T_{C}}^{T_{H}} c_{v} \frac{d T}{T} + R \ln (\frac{V_{2} - n b}{V_{1} - n b}) = 0 \end{array}$

La primera integral solamente depende de T

Transformación 2--->3, expansión isoterma a temperatura T_H entre V₂ y V₃

$\begin{array}{l} W_{23} = \int_{V_{2}}^{V_{3}} p d V = \int_{V_{2}}^{V_{3}} (\frac{n R T_{H}}{V - n b} - \frac{n^{2} a}{V^{2}}) d V = n R T_{H} \ln (\frac{V_{3} - n b}{V_{2} - n b}) + \frac{n^{2} a}{V_{3}} - \frac{n^{2} a}{V_{2}} \\ Q_{23} = \int_{V_{2}}^{V_{3}} T_{H} \frac{n R}{V - n b} d V = n R T_{H} \ln (\frac{V_{3} - n b}{V_{2} - n b}) \end{array}$

Transformación 3--->4, expansión adiabática entre V₃ y V₄

$W_{34} = \int_{V_{3}}^{V_{4}} p d V = - n c_{v} (T_{C} - T_{H}) + \frac{n^{2} a}{V_{4}} - \frac{n^{2} a}{V_{3}}$

El calor Q₃₄=0

$\begin{array}{l} δ Q = n c_{v} d T + T \frac{n R}{V - n b} d V = 0 \\ \int_{T_{H}}^{T_{C}} c_{v} \frac{d T}{T} + R \int_{V_{3}}^{V_{4}} \frac{d V}{V - n b} = 0 \\ \int_{T_{H}}^{T_{C}} c_{v} \frac{d T}{T} + R \ln (\frac{V_{4} - n b}{V_{3} - n b}) = 0 \end{array}$

Transformación 4--->1, el gas se comprime isotermicamente a temperatura T_C entre V₄ y V₁

$\begin{array}{l} W_{41} = \int_{V_{4}}^{V_{1}} p d V = \int_{V_{4}}^{V_{1}} (\frac{n R T_{C}}{V - n b} - \frac{n^{2} a}{V^{2}}) d V = n R T_{C} \ln (\frac{V_{1} - n b}{V_{4} - n b}) + \frac{n^{2} a}{V_{1}} - \frac{n^{2} a}{V_{4}} \\ Q_{41} = \int_{V_{4}}^{V_{1}} T_{C} \frac{n R}{V - n b} d V = n R T_{C} \ln (\frac{V_{1} - n b}{V_{4} - n b}) \end{array}$

Ciclo completo

Trabajo, W=W₁₂+W₂₃+W₃₄+W₄₁

$W = n R T_{H} \ln (\frac{V_{3} - n b}{V_{2} - n b}) + n R T_{C} \ln (\frac{V_{1} - n b}{V_{4} - n b}) = n R T_{H} \ln (\frac{V_{3} - n b}{V_{2} - n b}) - n R T_{C} \ln (\frac{V_{4} - n b}{V_{1} - n b})$

Calor absorbido en la expansión isotérmica a la temperatura T_H

$Q_{23} = n R T_{H} \ln (\frac{V_{3} - n b}{V_{2} - n b})$

Calor cedido cuando el gas se comprime isotérmicamente a la temperatura T_C

$Q_{41} = n R T_{C} \ln (\frac{V_{1} - n b}{V_{4} - n b}) = - n R T_{C} \ln (\frac{V_{4} - n b}{V_{1} - n b})$

El rendimiento del ciclo es

$η = \frac{W}{Q_{23}} = \frac{n R T_{H} \ln (\frac{V_{3} - n b}{V_{2} - n b}) - n R T_{C} \ln (\frac{V_{4} - n b}{V_{1} - n b})}{n R T_{H} \ln (\frac{V_{3} - n b}{V_{2} - n b})} = 1 - \frac{T_{C} \ln (\frac{V_{4} - n b}{V_{1} - n b})}{T_{H} \ln (\frac{V_{3} - n b}{V_{2} - n b})}$

Teniendo en cuenta las relaciones obtenidas en las transformaciones adiabáticas

$\begin{array}{l} {\begin{cases} \int_{T_{C}}^{T_{H}} c_{v} \frac{d T}{T} + R \ln (\frac{V_{2} - n b}{V_{1} - n b}) = 0 \\ \int_{T_{H}}^{T_{C}} c_{v} \frac{d T}{T} + R \ln (\frac{V_{4} - n b}{V_{3} - n b}) = 0 \end{cases} \\ \ln (\frac{V_{2} - n b}{V_{1} - n b}) + \ln (\frac{V_{4} - n b}{V_{3} - n b}) = 0 \\ \ln (\frac{V_{4} - n b}{V_{1} - n b}) = \ln (\frac{V_{3} - n b}{V_{2} - n b}) \end{array}$

Obtenemos la misma expresión del redimiento del ciclo de Carnot η que para un gas ideal

$η = 1 - \frac{T_{C}}{T_{H}}$

Referencias

D C Agrawal, V J Menon. The Carnot cycle with the van der Waals equation of state. Eur. J. Phys 11, (1990). pp. 88 - 90

Kiran S. Kumar, Aravind P. Babu, M. Ponmurugan. Van der Waal’s gas equation for an adiabatic process and its Carnot engine efficiency. Physics Education. Jul-Sep 2017