Una escopeta de bambú consiste en un tubo de radio r, que tiene un tapón (bala) de masa m en su extremo izquierdo, el radio del tapón cilíndrico es r y su longitud es d.

En el extremo derecho, otro tapón ajustado al tubo cilíndrico sujeto a una varilla, se mueve con velocidad constante u, comprimiendo el aire existente entre ambos. La figura, representa el estado inicial, t=0, la presión del aire encerrado es la presión atmosférica p₀.

En el instante t, el volumen de aire comprimido habrá disminuido y su presión p habrá aumentado. Supondremos que la transformación entre los dos estados es adiabática

${\displaystyle p{\left(L_0-ut\right)}^{\gamma }=p_0{L}_0^{\gamma }}$

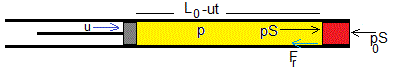
Las fuerzas sobre la bala serán

• la que ejerce el aire comprimido, pS=pπr²
• la que ejerce la presión atmosférica, p₀S=p₀πr²
• la fuerza de rozamiento F_r entre la superficie de la bala y la superficie interior del tubo

En el equilibrio

${\displaystyle \begin{array}{l}p\pi r^2=p_0\pi r^2+F_r\\ F_r=\left(p-p_0\right)\pi r^2\end{array}}$

Presión y longitud críticas

Para una presión p_s la fuerza de rozamiento F_r alcanzará su valor máximo F_s, la bala empezará a deslizar a lo largo del tubo, la longitud crítica L_s de la columna de aire comprimido será

${\displaystyle \begin{array}{l}{p}_s{L}_s^{\gamma }=p_0{L}_0^{\gamma }\\ p_s\pi r^2=p_0\pi r^2+F_s\end{array}}$

Despejamos la longitud crítica L_s, que se alcanza en el instante t_s, tal que L_s=L₀-ut_s

${\displaystyle L_s=\frac{L_0}{{\left(1+\frac{F_s}{p_0\pi r^2}\right)}^{1/\gamma }}}$

Datos

• presión atmosférica, p₀=101 300 Pa
• radio del tubo y de la bala, r=0.35 cm
• índice adiabático del aire, γ=1.4
• longitud inicial de la columna de aire comprimido, L₀=28 cm
• valor máximo de la fuerza de rozamiento estando la bala en reposo, F_s=76.2 N

p0=101300; %presión atmosférica
r=0.0035; %radio del tubo
gamma=1.4; %indice adiabático
Fs=76.2; %rozamiento estático
L0=0.28; %longitud inicial
Ls=L0/(1+Fs/(p0*pi*r^2))^(1/gamma);
disp(Ls*100)
ps=(L0/Ls)^gamma;
disp(ps)

    3.2322
   20.5461

La longitud de la columna de aire comprimido es L_s=3.2 cm, la presión crítica es p_s=20.5 atm

Movimiento de la bala en el tubo

Comparamos el estado en el instante t_s cuando la bala empìeza a moverse, con el estado en un instante posterior t, cuando ya se mueve y empieza a salir del tubo

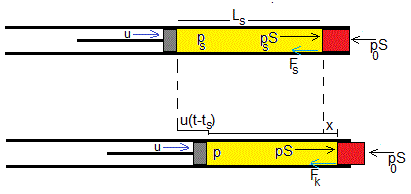
Cuando la bala empieza a moverse la fuerza de rozamiento disminuye al valor F_k. La ecuación del movimiento y de la transformación adiabática son

${\displaystyle \begin{array}{l}m\frac{d^{2}x}{d{t}^2}=\left(p-p_0\right)\pi r^2-F_k\\ p{\left(L_s-u\left(t-t_s\right)+x\right)}^{\gamma }=p_0{L}_0^{\gamma }\end{array}}$

Obtenemos la ecuación diferencial

${\displaystyle \frac{d^{2}x}{d{t}^2}=\frac{p_0\pi r^2}{m}{\left(\frac{L_0}{L_s-u\left(t-t_s\right)+x}\right)}^{\gamma }-\frac{p_0\pi r^2+F_k}{m}}$

Se resuelve esta ecuación diferencial por el procedimiento ode45 de MATLAB con las siguientes condiciones iniciales, en el instante t=t_s, x=0, y dx/dt=0. Se interumpe el proceso de integración cuando la bala sale del tubo, x=d

Datos adicionales

• masa de la bala, m=0.0009 kg
• longitud de la bala, d=1 cm
• velocidad constante de la varilla, u=1 m/s
• fuerza de rozamiento cuando la bala está en movimiento, F_k=13.2 N

Representamos la velocidad v de la bala en función de la posición x dentro del tubo, hasta que sale x=d

function bambu_1
    p0=101300; %presión atmosférica
    r=0.007/2; %radio del tubo
    d=0.01; %longitud de la bala
    m=0.0009; %masa de la bala
    gamma=1.4; %índice adiabático
    Fs=76.2; %rozamiento estático
    Fk=13.2; %rozamiento cinético
    L0=0.28; %longitud inicial
    Ls=L0/(1+Fs/(p0*pi*r^2))^(1/gamma);
    disp(Ls*100)
    u=1; %velocidad de la varilla

    opts=odeset('events',@stop_bambu);
    f=@(t,x)[x(2);p0*pi*r^2*(L0/(Ls-u*t+x(1)))^gamma/m-(Fk+p0*pi*r^2)/m];
    [t,x]=ode45(f,[0,1],[0,0],opts);
    disp([t(end),x(end,2)])
    plot(x(:,1),x(:,2))
    xlim([0,0.01])
    grid on
    xlabel('x')
    ylabel('v');
    title('Escopeta de bambú')


    function [value,isterminal,direction]=stop_bambu(~,x)
        value=x(1)-d;
        isterminal=1;    
        direction=1; 
    end
end

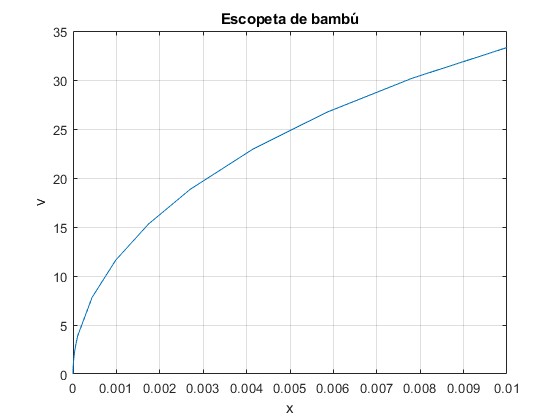
    0.0006   33.3110

La velocidad final de la bala es v₀=33.3 m/s, emplea un tiempo de 6·10^-4 s en salir del tubo contado desde el instante inicial t_s

Solución analítica aproximada

Despreciamos el término x frente a L_s-u(t-t_s). La ecuación diferencial del movimiento se expresa

${\displaystyle \frac{d^{2}x}{d{t}^2}\approx \frac{p_0\pi r^2}{m}{\left(\frac{L_0}{L_s-u\left(t-t_s\right)}\right)}^{\gamma }-\frac{p_0\pi r^2+F_k}{m}}$

Integramos para obtener la velocidad v de la bala en función del tiempo t

${\displaystyle \begin{array}{l}\frac{dv}{dt}\approx \frac{p_0\pi r^2}{m}{\left(\frac{L_0}{L_s-u\left(t-t_s\right)}\right)}^{\gamma }-\frac{p_0\pi r^2+F_k}{m}\\ {\displaystyle \underset{0}{\overset{v}{\int }}dv}=\frac{p_0\pi r^2}{m}{L}_0^{\gamma }{\displaystyle \underset{t_s}{\overset{t}{\int }}\frac{dt}{{\left(L_s-u\left(t-t_s\right)\right)}^{\gamma }}}-\frac{p_0\pi r^2+F_k}{m}{\displaystyle \underset{t_s}{\overset{t}{\int }}dt}\\ v=\frac{p_0\pi r^2}{m}{L}_0^{\gamma }\frac{L_s^{-\gamma +1}-{\left(L_s-u\left(t-t_s\right)\right)}^{-\gamma +1}}{u\left(-\gamma +1\right)}-\frac{p_0\pi r^2+F_k}{m}\left(t-t_s\right)\end{array}}$

Integramos de nuevo, para obtener el desplazamiento x de la bala en función del tiempo t

${\displaystyle \begin{array}{l}\frac{dx}{dt}=\frac{p_0\pi r^2}{m}{L}_0^{\gamma }\frac{L_s^{-\gamma +1}-{\left(L_s-u\left(t-t_s\right)\right)}^{-\gamma +1}}{u\left(-\gamma +1\right)}-\frac{p_0\pi r^2+F_k}{m}\left(t-t_s\right)\\ x=\frac{p_0\pi r^2}{m}\frac{L_0^{\gamma }}{u\left(-\gamma +1\right)}\left\{L_s^{-\gamma +1}\left(t-t_s\right)+\frac{1}{u\left(-\gamma +2\right)}\left\{{\left(L_s-u\left(t-t_s\right)\right)}^{-\gamma +2}-L_s^{-\gamma +2}\right\}\right\}-\frac{p_0\pi r^2+F_k}{2m}{\left(t-t_s\right)}^2\end{array}}$

Cuando x=d, la bala ha salido del tubo, el instante t_f es la raíz de la ecuación transcendente

${\displaystyle d=\frac{p_0\pi r^2}{m}\frac{L_0^{\gamma }}{u\left(-\gamma +1\right)}\left\{L_s^{-\gamma +1}\left(t-t_s\right)+\frac{1}{u\left(-\gamma +2\right)}\left\{{\left(L_s-u\left(t-t_s\right)\right)}^{-\gamma +2}-L_s^{-\gamma +2}\right\}\right\}-\frac{p_0\pi r^2+F_k}{2m}{\left(t-t_s\right)}^2}$

Resolvemos la ecuación transcendente utilizando fzero de MATLAB, una vez calculado t_f obtenemos la velocidad final de la bala v(t_f)

p0=101300; %presión atmosférica
r=0.0035; %radio del tubo
d=0.01; %longitud de la bala
m=0.0009; %masa de la bala
gamma=1.4; %índice adiabático
Fs=76.2; %rozamiento estático
Fk=13.2; %rozamiento cinético
L0=0.28; %longitud inicial
Ls=L0/(1+Fs/(p0*pi*r^2))^(1/gamma);
disp(Lc*100)
u=1; %velocidad de la varilla
f=@(t) p0*pi*r^2*L0^gamma*(Ls^(-gamma+1)*t+((Ls-u*t)^(-gamma+2)-
Ls^(-gamma+2))/(u*(-gamma+2)))/(m*u*(-gamma+1))-(p0*pi*r^2+Fk)*t^2/(2*m)-d;
tf=fzero(f,[0,0.01]);
v=@(t) p0*pi*r^2*L0^gamma*(Ls^(-gamma+1)-(Ls-u*t)^(-gamma+1))/
(m*u*(-gamma+1))-(p0*pi*r^2+Fk)*t/m;
disp(tf)
disp(v(tf))

   5.3191e-04
   37.7860

El tiempo que emplea la bala en salir del tubo, t_f-t_s=5.3·10^-4 s, alcanzando una velocidad final de v₀=37.8 m/s

Movimiento de la bala después del disparo

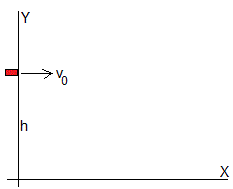
Situamos la escopeta de bambú sobre una mesa a una altura h=60 cm sobre el suelo

Si no se considera el rozamiento con el aire, las ecuaciones del tiro parabólico serían

${\displaystyle \{\begin{array}{l}{a}_x=0\\ a_y=g\end{array}\{\begin{array}{l}{v}_x=v_0\\ v_y=-gt\end{array}\{\begin{array}{l}x=v_{0}t\\ y=h-\frac{1}{2}g{t}^2\end{array}}$

Dado que la altura h es pequeña, 60 cm, el rozamiento de la bala con el aire es significativo solamente en el movimiento horizontal

${\displaystyle m\frac{d{v}_x}{dt}=-\frac{1}{2}{C}_d\rho \pi r^2{v}_x^2}$

donde ρ=1.29 kg/m³ es la densidad del aire y C_d≈1.15 es el coeficiente de arrastre

Integramos la ecuación diferencial para obtener la componente horizontal de la velocidad v_x

${\displaystyle \begin{array}{l}\frac{d{v}_x}{dt}=-b{v}_x^2,b=\frac{1}{2m}{C}_d\rho \pi r^2\\ {\displaystyle \underset{v_0}{\overset{v}{\int }}\frac{d{v}_x}{v_x^2}}=-b{\displaystyle \underset{0}{\overset{t}{\int }}dt}\\ -\frac{1}{v_x}+\frac{1}{v_0}=-bt\\ v_x=\frac{v_0}{1+b{v}_{0}t}\end{array}}$

Integramos de nuevo

${\displaystyle \begin{array}{l}\frac{dx}{dt}=\frac{v_0}{1+b{v}_{0}t}\\ x=v_0{\displaystyle \underset{0}{\overset{t}{\int }}\frac{dt}{1+b{v}_{0}t}}\\ x=\frac{1}{b}\ln \left(1+b{v}_{0}t\right)\end{array}}$

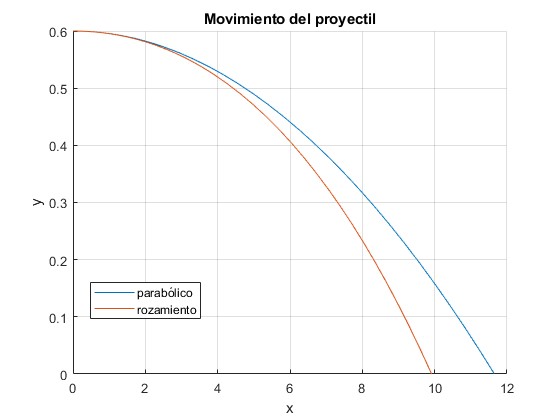
Representamos la trayectoria seguida por el proyectil, con y sin rozamiento

m=0.0009; %masa de la bala
 Cd=1.15; %coeficiente de arrastre
 r=0.0035; %radio del tubo
 rho=1.29; %densidad del aire
 b=Cd*rho*pi*r^2/(2*m);
 h=0.6; %altura
 hold on
 v0=33.3; %velocidad inicial de la bala
 x=@(t) v0*t;
 y=@(t) h-4.9*t.^2;
 fplot(x,y,[0,sqrt(h/4.9)]) %tiro parabólico
 x=@(t) log(1+b*v0*t)/b;
 fplot(x,y,[0,sqrt(h/4.9)]) %con rozamiento
 hold off
 grid on
 xlabel('x')
 legend('parabólico','rozamiento','Location', 'best')
 ylabel('y')
 title('Movimiento del proyectil')

Referencias

Ardi Khalifah, Mikrajuddin Abdullah. Physics of Bamboo Rifle