Un gas se expande adiabáticamente
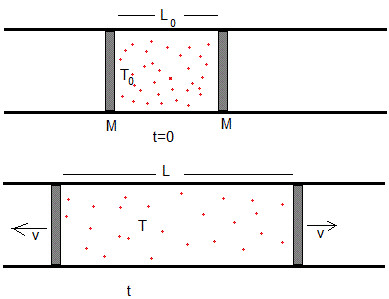
Consideremos n moles de un gas ideal monoatómico encerrado entre dos émbolos de sección A y de masa M. Los émbolos pueden deslizar sin rozamiento alguno una vez liberados. Inicialmente, el gas está a la temperatura T0 y los émbolos están separados una distancia L0. Se liberan los pistones y queremos determinar en el instante t, temperatura T del gas, la velocidad v de los émbolos y la distancia L entre los mismos.
La energía interna inicial del gas ideal monoatómico es U=n·cv·T0
En el instante t, la energía del sistema es la suma de la energía cinética de los émbolos, y la energía interna del gas ideal a la temperatura T<T0
Como la velocidad de un émbolo v=d(L/2)/dt, tenemos que
Si el gas experimenta una transformación adiabática, se cumple p·Vγ=cte, o bien
El recipiente tiene sección constante A.
Para obtener como cambia la separación L entre émbolos o la temperatura T del gas con el tiempo t, derivamos esta última ecuación de la transformación adiabática respecto del tiempo.
Expresamos esta ecuación en términos de la temperatura T, empleando la transformación adiabática
Introduciendo la expresión de la velocidad v del émbolo
Para un gas monoatómico, cv=3R/2 y γ=cp/cv=5/3
Nos queda una ecuación diferencial en T, que simplificamos para prepararla para su posterior integración
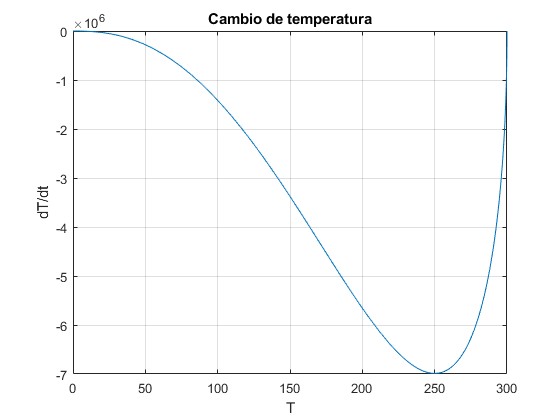
Representamos el cambio de temperatura dT/dt en función de T
T0=300;
f=@(T) -T.^(5/2).*sqrt(T0-T);
fplot(f,[0,T0])
grid on
xlabel('T')
ylabel('dT/dt')
title('Cambio de temperatura')
Integramos
Llamamos u=T/T0
Hacemos el cambio de variable u=sin2x
Hacemos el cambio z=cotx, 1+z2=1/sin2x, dz=-(1+z2)dx
Deshacemos los cambios
Calculamos la temperatura reducida u=T/T0 en función del tiempo t
Escribiendo z2=(1-u)/u, resolvemos la ecuación cúbica, z3+3z-c=0
Una vez calculado z se despeja u=1/(z2+1) y luego T=T0·u
Conocida la temperatura T calculamos la velocidad v de los émbolos
Cuando t tiende a infinito, la velocidad v de los émbolos tiende hacia un valor límite constante. La energía interna inicial del gas se convierte en energía cinética de los dos émbolos iguales
Datos: Tmperatura inicial, T0=300 K, número de moles, n=0.0447, constante de los gases, R=8.3143 J/(K·mol), masa de cada émbolo, M=0.1 kg, sepración inicial entre los dos émbolos L0=1 m
T0=300; %temperatura inicial
n=0.0447; %número de moles
R=8.3143; %constante de los gases
M=0.1; %masa de cada émbolo
L0=1; %separación inicial entre los dos émbolos
t=0:0.01:1.5; %tiempo
%calcla la raiz real de la ecuación cúbica
c=-sqrt(6*n*R*T0/M)*t/L0;
A=(abs(c/2)+sqrt((c/2).^2+1)).^(1/3);
z=A-1./A;
u=1./(z.^2+1);
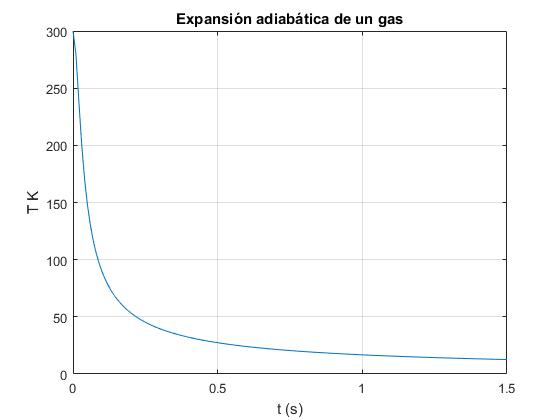
plot(t,T0*u)
grid on
xlabel('t (s)')
ylabel ('T K')
title('Expansión adiabática de un gas')
figure
v=sqrt(3*n*R*T0*(1-u)/(2*M));
plot(t,v)
grid on
xlabel('t (s)')
ylabel ('v (m/s)')
title('Expansión adiabática de un gas')
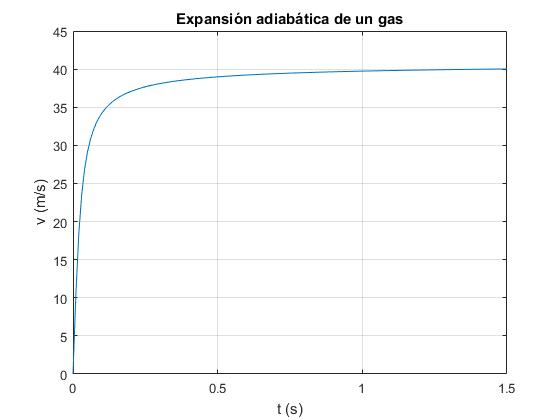
La velocidad límite que alcanzan los émbolos es
>> sqrt(3*n*R*T0/(2*M)) ans = 40.8952
Esta aproximación es válida siempre que se cumpla que la velocidad del émbolo v es mucho más pequeña que la velocidad vrms media de las moléculas del gas
Referencias
R. C. Amor, J.P.H.Esguerra. Evolution of ideal gas mixtures confined in an insulated container by two identical pistons. Am. J. Phys. 78, (9) September 2010, pp. 916-919

