Foco de capacidad calorífica finita

Gas ideal contenido en un recipiente cilíndrico en contacto con un foco de capacidad calorífica finita

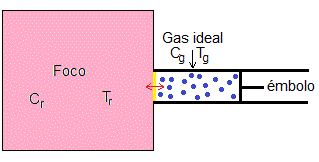
El sistema que estudiamos en este apartado, consiste en un gas ideal a la temperatura T_g y un foco de calor a temperatura T_r. El gas se puede comprimir o expandir mediante un émbolo

El foco de calor tiene tamaño finito y un volumen constante, por lo que su temperatura T_r puede cambiar debido al intercambio de calor con el gas δQ_r=-δQ_g. El gas y el foco están en todo momento en equilibrio térmico de modo que T_r=T_g=T.

Para el gas

dU_g=δQ_g-p·dV

U_g es la energía interna del gas, dU_g=n·c_v·dT, donde c_v es el calor calorífico a volumen constante del gas
Q_g es el calor absorbido por el gas, cedido por el foco
p·dV es e trabajo realizado

Para el foco de calor

dU_r=δQ_r=C_r·dT

C_r es la capacidad calorífica del foco cuyo volumen es constante

Supondremos que la capacidad calorífica C_r y el calor específico c_v se mantienen constantes durante el proceso

De las realaciones anteriores obtenemos

$\begin{array}{l} δ Q_{g} = n c_{v} \cdot d T + p \cdot d V \\ - C_{r} \cdot d T = n c_{v} \cdot d T + p \cdot d V \\ (n c_{v} + C_{r}) d T = - p \cdot d V = - \frac{- n R T}{V} d V \end{array}$

Integrando

$\begin{array}{l} \int \frac{(n c_{v} + C_{r}) d T}{T} = - \int \frac{n R}{V} d V \\ (n c_{v} + C_{r}) \ln T + n R \ln V = cte \\ \ln T + \frac{n R}{n c_{v} + C_{r}} \ln V = cte \\ T V^{\frac{n R}{n c_{v} + C_{r}}} = cte \\ p V^{\frac{n R}{n c_{v} + C_{r}} + 1} = cte \end{array}$

Teniendo en cuenta que el índice adiabático, c_p y c_v son los calores específicos a presión y volumen constantes del gas ideal

$γ = \frac{c_{p}}{c_{v}} = \frac{R + c_{v}}{c_{v}}$

Para el gas ideal contenido en el recipiente cilíndrico, nR=γC_g-C_g

La ecuación del proceso politrópico es

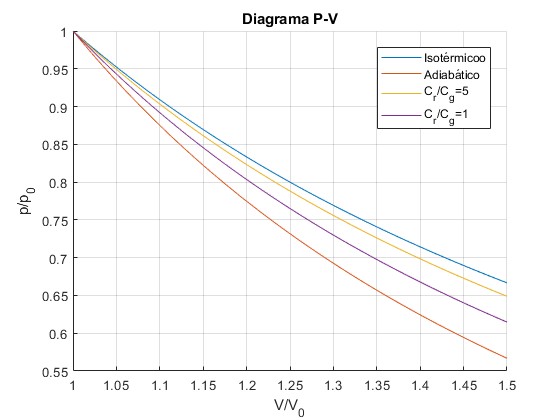
$p V^{β} = cte, β = \frac{n R}{n c_{v} + C_{r}} + 1 = \frac{n c_{v} γ + C_{r}}{n c_{v} + C_{r}} = \frac{γ + \frac{C_{r}}{n c_{v}}}{1 + \frac{C_{r}}{n c_{v}}}$

El proceso isotermo, β=1, se produce cuando C_r→∞ , el foco se hace muy grande y su temperatura permanece constante
El proceso adiabático, β=γ, se produce cuando C_r→0, el foco se hace muy pequeño y el gas ideal es un sistema aislado

Por tanto, 1≤β≤γ

La ecuación de estado de un gas ideal, pV=nRT

$\begin{array}{l} p V^{β + 1} = p_{0} V_{0}^{β + 1} \\ \frac{p}{p_{0}} = {(\frac{V_{0}}{V})}^{β + 1} \end{array}$

Representamos p/p₀ en función de V/V₀ para un gas diatómico (γ=1.4), donde p₀ y V₀ son las presión y volumen iniciales para un determinado proceso

hold on
fplot(@(x) 1./x,[1,1.5]) %isotermo
fplot(@(x) 1./x.^1.4,[1,1.5])%adiabático
beta=(1.4+5)/(1+5);
fplot(@(x) 1./x.^beta,[1,1.5]) %C_r/C_g=5
beta=(1.4+1)/(1+1);
fplot(@(x) 1./x.^beta,[1,1.5]) %C_r/C_g=1
hold off
grid on
xlabel('V/V_0')
ylabel('p/p_0')
legend('Isotérmicoo','Adiabático','C_r/C_g=5','C_r/C_g=1','Location','best')
title('Diagrama P-V')

Donde C_g=nc_v es la capacidad calorífica del gas

Representamos β en función del cociente C_r/C_g para γ=1.4

x=logspace(-2,2,100);
y=(1.4+x)./(1+x);
semilogx(x,y)
grid on
xlabel('C_r/C_g')
ylabel('\beta')
title('Indice \beta')

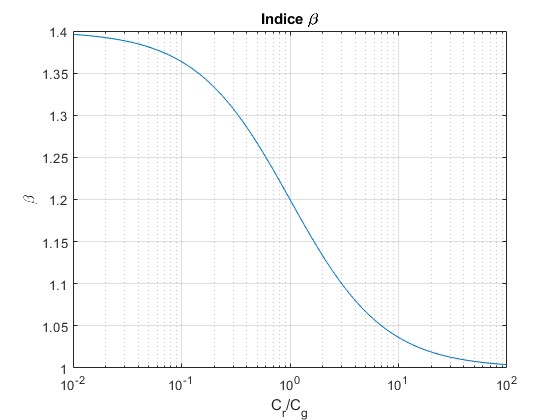
En la gráfica vemos que

C_r/C_g→0, β→γ, proceso adiabático
C_r/C_g→∞, β→1, proceso isotermo

Trabajo y calor

El trabajo es

$\begin{array}{l} W = \int_{V_{0}}^{V_{f}} p \cdot d V = \int_{V_{0}}^{V_{f}} \frac{cte}{V^{β}} \cdot d V = \frac{cte}{- β + 1} (V_{f}^{- β + 1} - V_{0}^{- β + 1}) = \frac{1}{- β + 1} (p_{f} V_{f} - p_{0} V_{0}) = \\ - \frac{n R}{\frac{n R}{n c_{v} + C_{r}}} (T_{f} - T_{0}) = - (n c_{v} + C_{r}) (T_{f} - T_{0}) \end{array}$

El calor

$Q = - C_{r} \int_{T_{0}}^{T_{f}} d T = - C_{r} (T_{f} - T_{0})$

Ejemplos

En este apartado, calculamos el índice β de un sistema formado por aire (supuesto gas ideal) y un foco finito de calor que podría ser: aire, agua o arena

Aire, aire

El gas ideal es aire que ocupa 10 l a la temperatura ambiente
El foco finito es 0.1 l de aire a temperatura ambiente

El aire es un gas diatómico, calor específico a volumen constante c_v=5R/2=5·8.3143/2 J/(K·mol)

El número de moles que contienen 10 l de aire es n=1.29kg/m³·0.01m³/28.84·10^-3 kg/mol

La capacidad calorífica de 10 l de aire es C_g=nc_v=9.29737≈9.3 J/K.

La capacidad calorífica de 0.1 l de aire es C_r=0.093 J/K

$β = \frac{γ + \frac{C_{r}}{C_{g}}}{1 + \frac{C_{r}}{C_{g}}} = \frac{1.4 + \frac{0.093}{9.3}}{1 + \frac{0.093}{9.3}} = 1.396$

Aire, agua

El gas ideal es aire que ocupa 10 l a la temperatura ambiente
El foco finito es 0.2 l de agua a temperatura ambiente

El calor específico del agua es c_v=4.186 J/(g·K).

La capacidad calorífica de 200 g de agua es C_r=200·4.186=837.2 J/K

$β = \frac{1.4 + \frac{837.2}{9.3}}{1 + \frac{837.2}{9.3}} = 1.004$

Aire, arena

El gas ideal es aire que ocupa 10 l a la temperatura ambiente
El foco finito es 20 g de arena a temperatura ambiente. Su capacidad calorífica es C_r=20 J/K

$β = \frac{1.4 + \frac{20}{9.3}}{1 + \frac{20}{9.3}} = 1.1270$

Transformación 1-->2 adiabática

$\begin{array}{l} T_{C} V_{1}^{γ - 1} = T_{H} V_{2}^{γ - 1} \\ 300 \cdot 1 = 400 \cdot V_{2}^{γ - 1}, V_{2} = 0.6495 m^{3} \end{array}$

Ciclo de Carnot

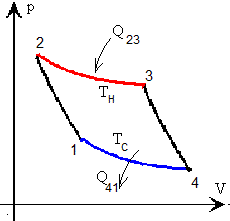
Hemos estudiado el ciclo de Carnot, en este apartado estudiamos el siguiente ejemplo

Los datos iniciales son los que figuran en la tabla adjunta. A partir de estos datos, hemos de rellenar los huecos de la tabla.

Variables	1	2	3	4
Presión p (kPa)	200
Volumen V (m³)	1		1.5
Temperatura T (K)	300	400	400	300

La temperatura del foco calientes T_H=400 K y la temperatura del foco frío es T_C=300 K

Para un gas monoatómico c_v=3R/2, c_p=5R/2, γ=c_p/c_v=5/3

La ecuación de estado de un gas ideal es p·V=nR·T. El número de moles

$n = \frac{p_{1} V_{1}}{R T_{c}} = \frac{200 \cdot 10^{3} \cdot 1}{8.3143 \cdot 300} = 80.1831$

En un proceso adiabático, $p V^{γ} = cte, T V^{γ - 1} = cte$

En este proceso isotérmico, p·V=cte

Transformación 1-->2, adiabática

$\begin{array}{l} T_{C} V_{1}^{γ - 1} = T_{H} V_{2}^{γ - 1} \\ 300 \cdot 1 = 400 \cdot V_{2}^{γ - 1}, V_{2} = 0.6495 m^{3} \\ p_{2} V_{2} = n R T_{H}, p_{2} = 410.56 kPa \end{array}$

Transformación 2-->3, isotérmica a la temperatura T_H

$p_{2} V_{2} = p_{3} V_{3}, p_{3} = 177.78 kPa$

Transformación 3-->4, adiabática

$\begin{array}{l} T_{H} V_{3}^{γ - 1} = T_{C} V_{4}^{γ - 1}, V_{4} = 2.3094 m^{3} \\ p_{4} V_{4} = n R T_{C}, p_{4} = 86.60 kPa \end{array}$

Transformación 3-->4, isotérmica a la temperatura T_C

Representamos el ciclo de Carnot

En color rojo, línea gruesa, se muestra la transformación 2-->3 cuando el gas está en contacto con el foco caliente. En color azul, línea gruesa, se muestra la transformación 4--->1 cuando el gas está en contacto con el foco frío

%datos
TH=400;  % Temperatura del foco caliente
TC=300;  %temperatura del foco frío
v1=1;  %m^3
v3=1.5;
p1=200e3; %Pa
R=8.3143; %constante de los gases 
%gas monoatómico
gamma=5/3; % adibático, 7/5 para el diatómico
nMoles=p1*v1/(R*TC);

%1--->2, adiabático
v2=v1*(TH/TC)^(1/(1-gamma));
p2=nMoles*R*TH/v2;
%2--->3, isotermo
p3=nMoles*R*TH/v3;
%3--->4, adiabática
v4=v3*(TC/TH)^(1/(1-gamma));
p4=nMoles*R*TC/v4;
hold on
fplot(@(v) v, @(v) (p1*(v1./v).^gamma)/1000 ,[v2,v1])
fplot(@(v) v, @(v) (p2*(v2./v))/1000 ,[v2,v3],'color','r','linewidth',1.5)
fplot(@(v) v, @(v) (p3*(v3./v).^gamma)/1000 ,[v3,v4])
fplot(@(v) v, @(v) (p4*v4./v)/1000 ,[v1,v4],'color','b','linewidth',1.5)
plot(v1,p1/1000,'ro','markersize',3,'markerfacecolor','r')
text(v1+0.02,p1/1000,num2str(TC))
plot(v2,p2/1000,'ro','markersize',3,'markerfacecolor','r')
text(v2+0.02,p2/1000,num2str(TH))
plot(v3,p3/1000,'ro','markersize',3,'markerfacecolor','r')
text(v3+0.02,p3/1000,num2str(TH))
plot(v4,p4/1000,'ro','markersize',3,'markerfacecolor','r')
text(v4+0.02,p4/1000,num2str(TC))
hold off
grid on
xlabel('v(m^3)')
ylabel('p(kPa)')
title('Ciclo de Carnot')

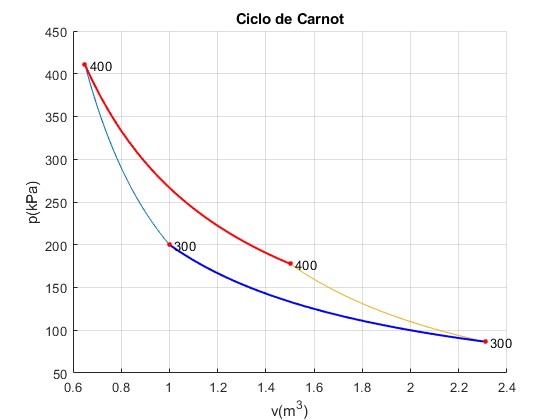
Calculamos el trabajo, calor

Transformación 1-->2, adiabática

Q₁₂=0

W₁₂=-n·c_v(T_H-T_C)=-100.00 kJ

Transformación 2-->3, isotérmica a la temperatura T_H

$Q_{23} = W_{23} = n R T_{H} \ln (\frac{V_{3}}{V_{2}}) = 223 . 20 k J$

Transformación 3-->4, adiabática

Q₃₄=0

W₃₄=-n·c_v(T_C-T_H)=100.00 kJ

Transformación 4-->1, isotérmica a la temperatura T_C

$Q_{41} = W_{41} = n R T_{C} \ln (\frac{V_{1}}{V_{4}}) = -167 . 40 k J$

Trabajo total, W=W₁₂+W₂₃+W₃₄+W₄₁=55.80 kJ

Calor total, Q=Q₂₃+Q₄₁=55.80 kJ

En un ciclo cerrado la variación de energía interna ΔU=0, por tanto Q=W

Añadimos el siguiente código al script anterior

%trabajo y calor
cV=3*R/2; %calor específico a volumen constante
W_12=-nMoles*cV*(TH-TC); %adiabático
W_23=nMoles*R*TH*log(v3/v2); %isotermo
Q_23=W_23;
W_34=-nMoles*cV*(TC-TH); %adiabático
W_41=nMoles*R*TC*log(v1/v4); %isotermo
Q_41=W_41; 
disp('Trabajo');
fprintf('W_12=%2.2f, W_23=%2.2f, W_34=%2.2f, W_41=%2.2f\n', W_12, W_23, W_34, W_41)
disp('Calor');
fprintf('Q_23=%2.2f, Q_41=%2.2f\n', Q_23, Q_41)
disp('Total')
W=W_12+W_23+W_34+W_41;
Q=Q_23+Q_41;
fprintf('Trabajo=%2.2f, Calor =%2.2f\n', W, Q);

Trabajo
W_12=-100000.00, W_23=223196.86, W_34=100000.00, W_41=-167397.64
Calor
Q_23=223196.86, Q_41=-167397.64
Total
Trabajo=55799.21, Calor =55799.21

Ciclo de Carnot con el foco caliente de capacidad calorífica finita

En el apartado anterior, el foco caliente y el foco frío tenían una capacidad calorífica infinita, sus temperaturas no cambiaban cuando la máquina térmica extraía calor del foco caliente y lo cedía al foco frío. En este apartado, supondremos que el foco caliente tiene una capacidad calorífica C_r finita, su temperatura T_H va a cambiar cuando el gas intercambia calor. El foco frío tiene una capacidad calorífica infinita por lo que su temperatura T_C permanece constante

Como hemos visto en el primer apartado, la transformación 2--->3 (expansión del gas) en contacto con un foco finito se describe mediante un proceso politrópico en vez de un proceso isotérmico

$p V^{β} = cte, β = \frac{γ + \frac{C_{r}}{n c_{v}}}{1 + \frac{C_{r}}{n c_{v}}}$

El clásico ciclo de Carnot se sustituye por los siguientes transformaciones

Los datos iniciales son los que figuran en la tabla adjunta. A partir de estos datos, hemos de rellenar los huecos de la tabla.

Variables	1	2	3	4
Presión p (kPa)	200
Volumen V (m³)	1		1.5
Temperatura T (K)	300	400		300

La temperatura inicial del foco finito caliente es T₂=400 K y la temperatura del foco frío es T_C=300 K

Supondremos que el exponente β=1.0835 bastante próximo a una transformación isotérmica β=1. Conocido β determinamos la capacidad calorífica del foco finito

$C_{r} = n c_{v} \frac{γ - β}{β - 1} = 6 984 .0 \frac{J}{K}$

Ciclo n° 1

Determinamos las incógnitas: presiones, volúmenes y temperaturas de los vértices a partir de los datos de la tabla y las transformaciones

Transformación 1-->2, adiabática

$\begin{array}{l} T_{C} V_{1}^{γ - 1} = T_{2} V_{2}^{γ - 1} \\ 300 \cdot 1 = 400 \cdot V_{2}^{γ - 1}, V_{2} = 0.6495 m^{3} \\ p_{2} V_{2} = n R T_{2}, p_{2} = 410.56 kPa \end{array}$

Transformación 2-->3, politrópica

$\begin{array}{l} T_{2} V_{2}^{β - 1} = T_{3} V_{3}^{β - 1} \\ 400 \cdot {0.6495}^{β - 1} = T_{3} \cdot {1.5}^{β - 1} T_{3} = 373 K \\ p_{3} V_{3} = n R T_{3}, p_{3} = 165.78 kPa \end{array}$

Transformación 3-->4, adiabática

$\begin{array}{l} T_{3} V_{3}^{γ - 1} = T_{C} V_{4}^{γ - 1}, V_{4} = 2 .0796 m^{3} \\ p_{4} V_{4} = n R T_{C}, p_{4} = 96.17 kPa \end{array}$

Transformación 4-->1, isotérmica a la temperatura T_C

Calculamos el trabajo, calor

Transformación 1-->2, adiabática

Q₁₂=0

W₁₂=-n·c_v(T₂-T_C)=-100.00 kJ

Transformación 2-->3, politrópica

$\begin{array}{l} W_{23} = - (n c_{v} + C_{r}) (T_{3} - T_{2}) = 215.57 kJ \\ Q_{23} = - C_{r} (T_{3} - T_{2}) = 188.57 kJ \end{array}$

Transformación 3-->4, adiabática

Q₃₄=0

W₃₄=-n·c_v(T_C-T₃)=73.00 kJ

Transformación 4-->1, isotérmica a la temperatura T_C

$Q_{41} = W_{41} = n R T_{C} \ln (\frac{V_{1}}{V_{4}}) = -146 . 43 k J$

Trabajo total, W=W₁₂+W₂₃+W₃₄+W₄₁=42.14 kJ

Calor total, Q=Q₂₃+Q₄₁=42.14 kJ

En un ciclo cerrado la variación de energía interna ΔU=0, por tanto Q=W

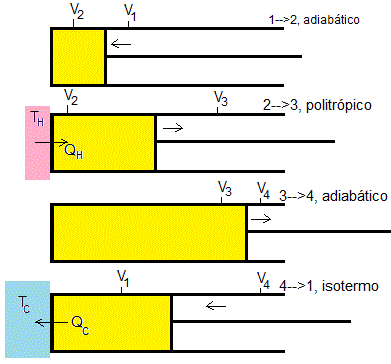
Representamos el ciclo de Carnot. Calculamos el calor y el trabajo en cada transformación.

En color rojo, línea gruesa, se muestra la transformación 2-->3 cuando el gas está en contacto con el foco finito inicialmente caliente. En color azul, línea gruesa, se muestra la transformación 4--->1 cuando el gas está en contacto con el foco frío

%datos
TH=400;  % Temperatura del foco finito
TC=300;  %temperatura del foco
v1=1;  %m^3
v3=1.5;
p1=200e3; %Pa
R=8.3143; %constante de los gases 
%gas monoatómico
gamma=5/3; % adibático, 
beta=1.0835; %politrópico
nMoles=p1*v1/(R*TC);

T2=TH; %temperatura incial del foco finito
nCiclos=60; %segundo ciclo
for k=1:nCiclos
    %1--->2 adibático
    v2=v1*(T2/TC)^(1/(1-gamma));
    p2=nMoles*R*T2/v2;
    %2--->3 politrópico
    T3=T2*(v3/v2)^(1-beta);
    p3=nMoles*R*T3/v3;
    %3--->4 adiabática
    v4=v3*(TC/T3)^(1/(1-gamma));
    p4=nMoles*R*TC/v4;
    %4--->1  isoterma
    if k==nCiclos
        break;
    end
     T2=T3; % temperatura final del foco finito caliente
end
    %trabajo
cV=3*R/2;  %calor específico, 
Cr=nMoles*cV*(beta-gamma)/(1-beta); %capacidad calorífica del foco finito
W_12=-nMoles*cV*(T2-TC); %adiabático
W_23=(nMoles*cV+Cr)*(T2-T3); %politrópico
Q_23=Cr*(T2-T3);
W_34=-nMoles*cV*(TC-T3); %adiabático
W_41=nMoles*R*TC*log(v1/v4); %isotermo
Q_41=W_41; 
disp('Trabajo');
fprintf('W_12=%2.2f, W_23=%2.2f, W_34=%2.2f, W_41=%2.2f\n', W_12, W_23, W_34, W_41)
disp('Calor');
fprintf('Q_23=%2.2f, Q_41=%2.2f\n', Q_23, Q_41)
disp('Total')
W=W_12+W_23+W_34+W_41;
Q=Q_23+Q_41;
fprintf('Trabajo=%2.2f, Calor =%2.2f\n', W, Q);
%gráfica del ciclo
hold on
fplot(@(v) v, @(v) (p1*(v1./v).^gamma)/1000 ,sort([v2,v1]))
fplot(@(v) v, @(v) (p2*(v2./v).^beta)/1000 ,[v2,v3],'color','r','lineWidth',1.5)
fplot(@(v) v, @(v) (p3*(v3./v).^gamma)/1000 ,sort([v3,v4]))
fplot(@(v) v, @(v) (p4*v4./v)/1000 ,[v1,v4],'color','b','lineWidth',1.5)
plot(v1,p1/1000,'ro','markersize',3,'markerfacecolor','r')
text(v1+0.02,p1/1000,num2str(TC))
plot(v2,p2/1000,'ro','markersize',3,'markerfacecolor','r')
text(v2+0.02,p2/1000,num2str(T2))
plot(v3,p3/1000,'ro','markersize',3,'markerfacecolor','r')
text(v3+0.02,p3/1000,num2str(T3))
plot(v4,p4/1000,'ro','markersize',3,'markerfacecolor','r')
text(v4+0.02,p4/1000,num2str(TC))
hold off
grid on
xlabel('V(m^3)')
ylabel('p(kPa)')
title('Ciclo de Carnot')

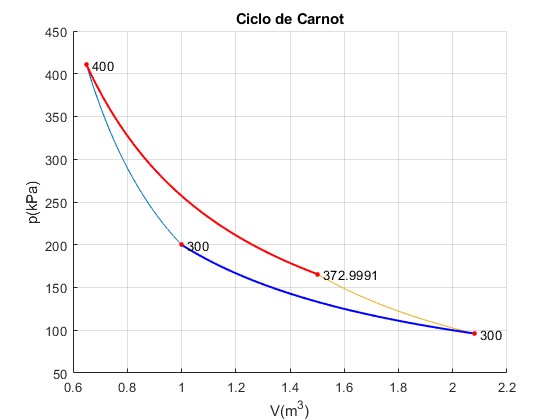
Trabajo
W_12=-100000.00, W_23=215575.98, W_34=72999.11, W_41=-146431.09
Calor
Q_23=188575.08, Q_41=-146431.09
Total
Trabajo=42144.00, Calor =42144.00

Ciclo n° 2

En el segundo ciclo, la temperatura inicial T₂ del foco finito caliente es la final de dicho foco T₃=373 K en el primer ciclo. En el código, asignamos T2=T3; %temperatura foco finito caliente. Cambiamos la sentencia nCiclos=2; %segundo ciclo

Transformación 1-->2, adiabática

$\begin{array}{l} T_{C} V_{1}^{γ - 1} = T_{2} V_{2}^{γ - 1} \\ 300 \cdot 1 = 373 \cdot V_{2}^{γ - 1}, V_{2} = 0.7213 m^{3} \\ p_{2} V_{2} = n R T_{2}, p_{2} = 344.74 kPa \end{array}$

Transformación 2-->3, politrópica

$\begin{array}{l} T_{2} V_{2}^{β - 1} = T_{3} V_{3}^{β - 1} \\ 375 \cdot {0.0.7213}^{β - 1} = T_{3} \cdot {1.5}^{β - 1} T_{3} = 350.88 K \\ p_{3} V_{3} = n R T_{3}, p_{3} = 155.95 kPa \end{array}$

Transformación 3-->4, adiabática

$\begin{array}{l} T_{3} V_{3}^{γ - 1} = T_{C} V_{4}^{γ - 1}, V_{4} = 1 .8973 m^{3} \\ p_{4} V_{4} = n R T_{C}, p_{4} = 105.41 kPa \end{array}$

Transformación 4-->1, isotérmica a la temperatura T_C

Calculamos el trabajo, calor

Transformación 1-->2, adiabática

Q₁₂=0

W₁₂=-n·c_v(T₂-T_C)=-73.00 kJ

Transformación 2-->3, politrópica

$\begin{array}{l} W_{23} = - (n c_{v} + C_{r}) (T_{3} - T_{2}) = 176.61 kJ \\ Q_{23} = - C_{r} (T_{3} - T_{2}) = 154.49 kJ \end{array}$

Transformación 3-->4, adiabática

Q₃₄=0

W₃₄=-n·c_v(T_C-T₃)=50.88 kJ

Transformación 4-->1, isotérmica a la temperatura T_C

$Q_{41} = W_{41} = n R T_{C} \ln (\frac{V_{1}}{V_{4}}) = -128 . 09 k J$

Trabajo total, W=W₁₂+W₂₃+W₃₄+W₄₁=26.40 kJ

Calor total, Q=Q₂₃+Q₄₁=26.40 kJ

En un ciclo cerrado la variación de energía interna ΔU=0, por tanto Q=W

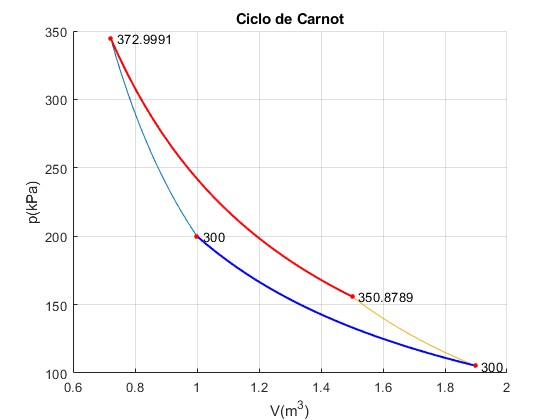
Trabajo
W_12=-72999.11, W_23=176608.73, W_34=50878.87, W_41=-128090.59
Calor
Q_23=154488.49, Q_41=-128090.59
Total
Trabajo=26397.89, Calor =26397.89

Ciclo n° 3

En el tercer ciclo, la temperatura inicial T₂ del foco finito caliente es la final T₃=350.88 K del segundo ciclo. En el código, cambiamos la sentencia en el script anterior nCiclos=3; %tercer ciclo

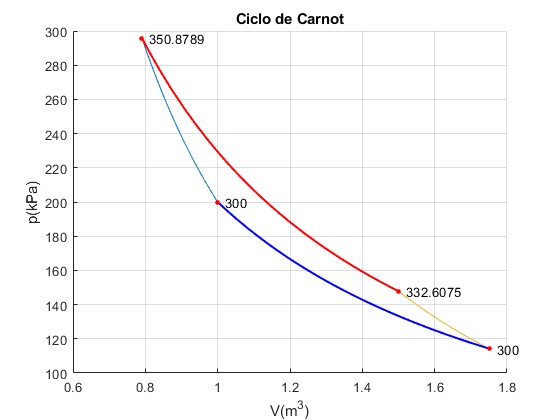
La temperatura del foco caliente finito se va reduciendo a T₃=332.6 K

Trabajo
W_12=-50878.87, W_23=145878.87, W_34=32607.54, W_41=-112047.25
Calor
Q_23=127607.54, Q_41=-112047.25
Total
Trabajo=15560.29, Calor =15560.29

El trabajo total se va reduciendo, como lo hace el área encerrada por el ciclo

Ciclo n° 6

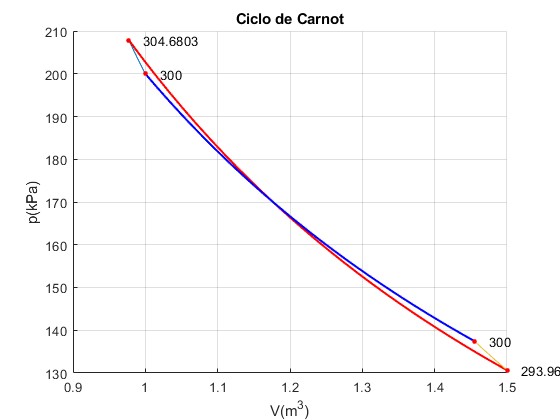
La temperatura inicial del foco finito caliente es T₂=304.7 K, al final se ha reducido a T₃=294 K por debajo de la temperatura del foco frío T_C=300 K. En la transformación 3-->4 el gas se comprime (trabajo negativo) en vez de expandirse. El trabajo total es casi nulo W=0.18 kJ.

Trabajo
W_12=-4680.27, W_23=85534.74, W_34=-6032.95, W_41=-74998.58
Calor
Q_23=74821.51, Q_41=-74998.58
Total
Trabajo=-177.07, Calor =-177.07

Ciclo n° 10

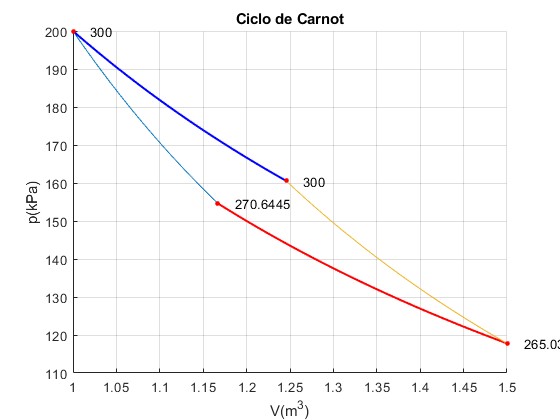
Trabajo
W_12=29355.49, W_23=44816.68, W_34=-34968.78, W_41=-43912.57
Calor
Q_23=39203.39, Q_41=-43912.57
Total
Trabajo=-4709.17, Calor =-4709.17

El dispositivo continúa funcionado como un figorífico, que toma calor del foco finito (ahora es el foco frío) durante la transformación politrópica 2-->3 (línea de color rojo) y lo cede al foco más caliente a la temperatura T_C durante la trsnformación isoterma 4--->1 (línea de color azul)

Ciclo n° 20

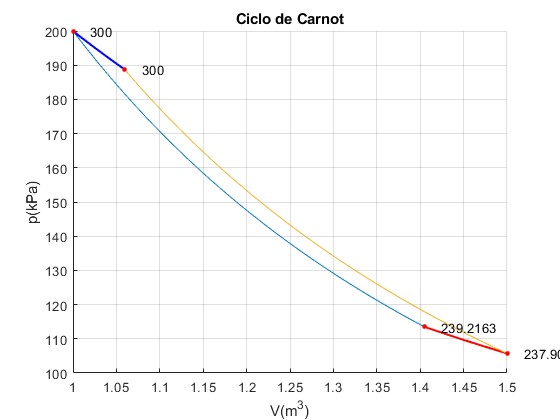
Trabajo
W_12=60783.69, W_23=10471.78, W_34=-62095.28, W_41=-11519.36
Calor
Q_23=9160.19, Q_41=-11519.36
Total
Trabajo=-2359.17, Calor =-2359.17

La temperatura del foco finito continúa decreciendo por debajo del foco frío T_C ya que se transfiere calor al gas desde el foco finito, cuando se expande

Ciclo n° 30

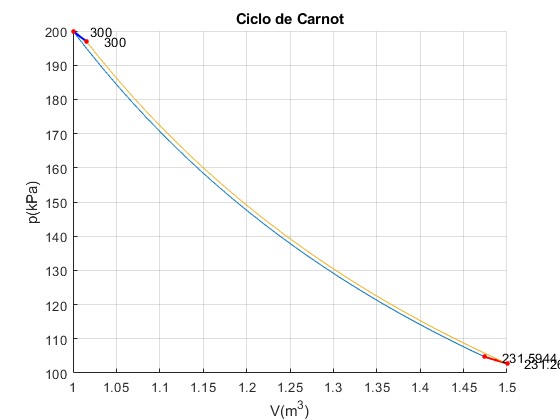
Trabajo
W_12=68405.65, W_23=2664.88, W_34=-68739.42, W_41=-3021.82
Calor
Q_23=2331.10, Q_41=-3021.82
Total
Trabajo=-690.71, Calor =-690.71

La transformación 2--->3 politrópica y la transformación 4--->1 se hacen cada vez más cortas. El trabajo neto, el área encerrda por el ciclo es cada vez más pequeña

Ciclo n° 60

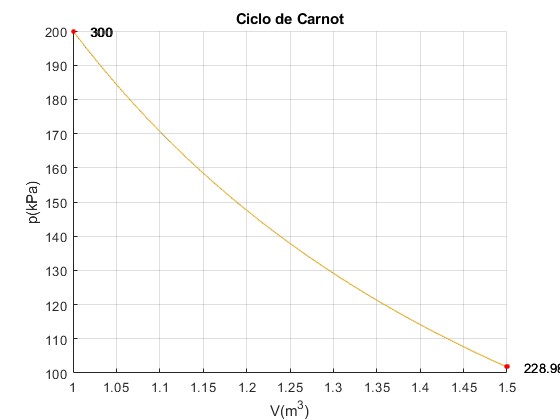
Trabajo
W_12=71009.56, W_23=47.60, W_34=-71015.52, W_41=-54.55
Calor
Q_23=41.64, Q_41=-54.55
Total
Trabajo=-12.91, Calor =-12.91

La transformación 2--->3 politrópica y la transformación 4--->1 han casi desaparecido, el émbolo se mueve hacia adelante y hacia atrás a través de una transformación adiabática que no genera trabajo neto, el área encerrada por el ciclo es cero. No se extrae calor del foco finito, su temperatura límite T_f=228.9 no cambia

Temperatura inicial y final del foco finito

Transformación 1-->2, adiabática

$\begin{array}{l} T_{C} V_{1}^{γ - 1} = T_{2} V_{2}^{γ - 1} \\ V_{2} = V_{1} {(\frac{T_{C}}{T_{2}})}^{\frac{1}{γ - 1}} \end{array}$

Transformación 2-->3, politrópica

$\begin{array}{l} T_{2} V_{2}^{β - 1} = T_{3} V_{3}^{β - 1} \\ T_{3} = T_{2} {(\frac{V_{2}}{V_{3}})}^{β - 1} \end{array}$

Relacionamos las temperaturas T₃ final del foco finito, y T₂ inicial del foco finito con los volúmenes fijos V₁ y V₃ y la temperatura T_C del foco frío

$\begin{array}{l} T_{3} = T_{2} {(\frac{V_{2}}{V_{3}})}^{β - 1} = T_{2} {(\frac{V_{1} {(\frac{T_{C}}{T_{2}})}^{\frac{1}{γ - 1}}}{V_{3}})}^{β - 1} = {(\frac{V_{1}}{V_{3}})}^{β - 1} T_{C}^{\frac{β - 1}{γ - 1}} T_{2}^{\frac{γ - β}{γ - 1}} \\ T_{3} = a T_{2}^{b}, {\begin{cases} a = {(\frac{V_{1}}{V_{3}})}^{β - 1} T_{C}^{\frac{β - 1}{γ - 1}} \\ b = \frac{γ - β}{γ - 1} \end{cases} \end{array}$

Ciclo n° 1

$\begin{array}{l} T_{2} = T_{H 0} \\ T_{3} = a {(T_{H 0})}^{b} \end{array}$

T_H0=400 K es la tmperatura inicial del foco caliente

Ciclo n° 2

$\begin{array}{l} T_{2} = a {(T_{H 0})}^{b} \\ T_{3} = a {(a {(T_{H 0})}^{b})}^{b} = a^{1 + b} {(T_{H 0})}^{b^{2}} \end{array}$

Ciclo n° 3

$\begin{array}{l} T_{2} = a^{1 + b} {(T_{H 0})}^{b^{2}} \\ T_{3} = a {(a^{1 + b} {(T_{H 0})}^{b^{2}})}^{b} = a^{1 + b + b^{2}} {(T_{H 0})}^{b^{3}} \end{array}$

Ciclo n° k

$\begin{array}{l} T_{2} = a^{1 + b + b^{2} + ... + b^{k - 2}} {(T_{H 0})}^{b^{k - 1}} \\ T_{3} = a^{1 + b + b^{2} + ... + b^{k - 1}} {(T_{H 0})}^{b^{k}} \end{array}$

El exponente es la suma de n=k-2 términos de una progresión geométrica cuyo a₀=1 y la razón r=b. Como 1<β<γ resulta b<1, y por tanto, la serie es convergente

$\begin{array}{l} S_{n} = a_{0} + a_{0} r + a_{0} r^{2} + a_{0} r^{3} + ... + a_{0} r^{n} \\ S_{n} = a_{0} \frac{1 - r^{n + 1}}{1 - r} = 1 \frac{1 - b^{k - 1}}{1 - b} = \frac{1 - b^{k - 1}}{1 - b} \end{array}$

Las temperaturas valen

$\begin{array}{l} T_{2} = a^{\frac{1 - b^{k - 1}}{1 - b}} {(T_{H 0})}^{b^{k - 1}} \\ T_{3} = a^{\frac{1 - b^{k}}{1 - b}} {(T_{H 0})}^{b^{k}} \end{array}$

Para el ciclo n° 10, la temperatura inicial del foco finito es T₂=270.6445 K y la temperatura final T₃=265.0312 K, tal como podemos ver en la figura correspondiente al ciclo n° 10

gamma=5/3; % adibático, 
beta=1.0835; %politrópico
v1=1; v3=1.5; Tc=300; TH=400;

b=(gamma-beta)/(gamma-1);
a=(1/1.5)^(beta-1)*TC^((beta-1)/(gamma-1));
k=10; %ciclo
T2=a^((1-b^(k-1))/(1-b))*TH^(b^(k-1)); %inicial
T3=a^((1-b^k)/(1-b))*TH^(b^k); %final
disp([T2, T3])

  270.6445  265.0312

Representamos la temperatura inicial T₂ (punto de color rojo) y final T₃ (punto de color azul) del foco finito en función de el número de ciclo k

gamma=5/3; % adibático, 
beta=1.0835; %politrópico
v1=1; v3=1.5; Tc=300; TH=400;

b=(gamma-beta)/(gamma-1);
a=(v1/v3)^(beta-1)*TC^((beta-1)/(gamma-1));
g=@(k) (a.^((1-b.^(k-1))/(1-b))).*(TH.^(b.^(k-1))); %temperatura inicial
f=@(k) (a.^((1-b.^k)/(1-b))).*(TH.^(b.^k)); %temperatura final
kk=1:60;
hold on
line([0,60],[TH,TH],'color','r')
line([0,60],[TC,TC],'color','b')
%hold on
plot(kk, g(kk),'ro','markersize',3,'markerfacecolor','r')
plot(kk, f(kk),'bo','markersize',3,'markerfacecolor','b')
hold off
ylim([220,410])
grid on
legend('inicial','final','location','best')
xlabel('k')
ylabel('T_2, T_3')
title('Temperaturas del foco')

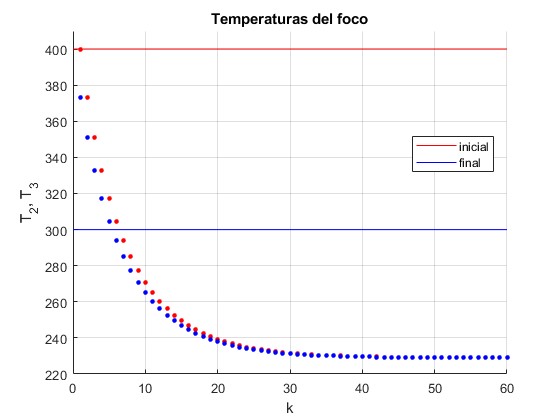
Cuando k se hace grande ambas temperaturas tienden hacia un valor límite T_f

$T_{f} = \lim_{k \to \infty} (a^{\frac{1 - b^{k}}{1 - b}} {(T_{H 0})}^{b^{k}}) = a^{\frac{1}{1 - b}} = {({(\frac{V_{1}}{V_{3}})}^{β - 1} T_{C}^{\frac{β - 1}{γ - 1}})}^{\frac{γ - 1}{β - 1}} = {(\frac{V_{1}}{V_{3}})}^{γ - 1} T_{C}$

Como b<1, b^k tiende a cero cuando k→∞

Con V₁=1 m³, V₂=1.5 m³ y T_C=300 K, la temperatura final es T_f=228.9428 K tal como puede verse en la figura correspondiente al ciclo n° 60

Como V₁<V₃, T_f<T_C. El foco finito inicialmente caliente (T_H= 400 K) termina siendo más frío (T_f=228.9 K) que el foco frío (T_C=300 K)

Trabajo y rendimiento

El trabajo se produce en las cuatro transformaciones del ciclo cerrado

El calor se produce en la transformación 2--->3 politrópica en contacto con el foco finito y en la 4--->1 isoterma en contacto con el foco frío

En un ciclo cerrado la variación de energía interna ΔU=0 por lo que el trabajo W y el calor Q son iguales, tal como se ha comprobado en la sección Ciclo de Carnot con el foco caliente de capacidad calorífica finita

$\begin{array}{l} W = Q = Q_{23} + Q_{41}, {\begin{cases} Q_{23} = C_{r} (T_{2} - T_{3}) > 0 \\ Q_{41} = n R T_{C} \ln (\frac{V_{1}}{V_{4}}) < 0 \end{cases} \\ η = \frac{W}{Q_{a b s}} = \frac{Q_{23} + Q_{41}}{Q_{23}} \end{array}$

En la transformación 3-->4, adiabática se cumple

$\begin{array}{l} T_{3} V_{3}^{γ - 1} = T_{C} V_{4}^{γ - 1} \\ V_{4} = V_{3} {(\frac{T_{3}}{T_{C}})}^{\frac{1}{γ - 1}} \end{array}$

Calculamos Q₂₃ y Q₄₁ para cada ciclo k

$\begin{array}{l} Q_{23} = C_{r} (T_{2} - T_{3}) \\ Q_{41} = n R T_{C} \ln (\frac{V_{1}}{V_{3}} {(\frac{T_{C}}{T_{3}})}^{\frac{1}{γ - 1}}) \end{array}$

gamma=5/3; % adibático, 
beta=1.0835; %politrópico
p1=200e3; v1=1; v3=1.5; TC=300; TH=400;
R=8.3143; %constante de los gases 
nMoles=p1*v1/(R*TC);
cV=3*R/2;  %calor específico, 
Cr=nMoles*cV*(beta-gamma)/(1-beta); %capacidad calorífica del foco finito

b=(gamma-beta)/(gamma-1);
a=(1/1.5)^(beta-1)*TC^((beta-1)/(gamma-1));
k=6; %ciclo
T2=a^((1-b^(k-1))/(1-b))*TH^(b^(k-1)); %inicial
T3=a^((1-b^k)/(1-b))*TH^(b^k); %final
Q_23=Cr*(T2-T3);
Q_41=nMoles*R*TC*log(v1*(TC/T3)^(1/(gamma-1))/v3);
fprintf('Trabajo=%2.2f, Calor absorbido=%2.2f\n', Q_23+Q_41, Q_23);

Trabajo=-177.07, Calor absorbido=74821.51

Para k=6 el trabajo es W=-177.07 J coincide con el valor obtenido para el ciclo n° 6

Representamos el rendimiento η en función del n° de ciclo k

gamma=5/3; % adibático, 
beta=1.0835; %politrópico
p1=200e3; v1=1; v3=1.5; TC=300; TH=400;
R=8.3143; %constante de los gases 
nMoles=p1*v1/(R*TC);
cV=3*R/2;  %calor específico, 
Cr=nMoles*cV*(beta-gamma)/(1-beta); %capacidad calorífica del foco finito

b=(gamma-beta)/(gamma-1);
a=(1/1.5)^(beta-1)*TC^((beta-1)/(gamma-1));
k=2; %ciclo
g=@(k) (a.^((1-b.^(k-1))/(1-b))).*(TH.^(b.^(k-1))); %temperatura inicial
f=@(k) (a.^((1-b.^k)/(1-b))).*(TH.^(b.^k)); %temperatura final
kk=1:60;
T2=a^((1-b^(k-1))/(1-b))*TH^(b^(k-1)); %inicial
T3=a^((1-b^k)/(1-b))*TH^(b^k); %final
Q_23=Cr*(g(kk)-f(kk));
Q_41=nMoles*R*TC*log(v1*(TC./f(kk)).^(1/(gamma-1))/v3);
W=Q_23+Q_41;
eta=W./Q_23;
plot(kk, eta,'ro','markersize',3,'markerfacecolor','r')
grid on
xlabel('k')
ylabel('\eta')
title('Rendimiento')

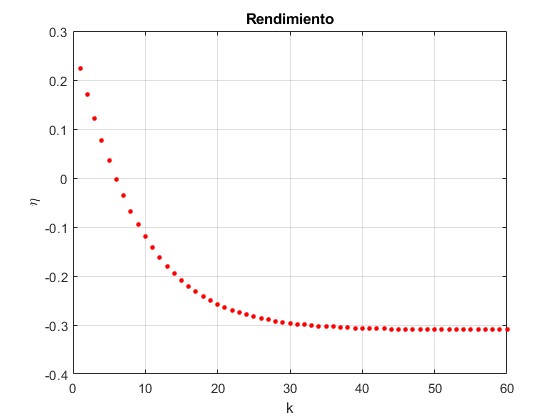
Cuando k>5, la máquina térmica se convierte en frigorífico, la medida relevante es el coeficiente K=-1/η que tiende al valor límite K_∞=3.22

Referencias

Yu-Han Ma. Simple realization of the polytropic process with a finite-sized reservoir. Am. J. Phys. 91 (7), July 2023. pp. 555-558

Randall D.Knight. Heat engines with finite reservoirs. Am. J. Phys. 92 (10), October 2024. pp. 759-764