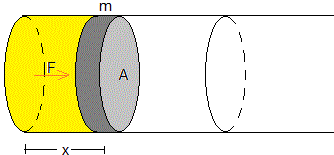
En primer lugar, consideramos un modelo simplificado del movimiento de la bala en tubo del cañón propulsada por un gas a presión. Supondremos:

• que la bala se mueve sin rozamiento
• que la presión atmosférica es despreciable frente a la presión del gas
• que la expansión del gas es adiabática

El gas a alta presión está inicialmente contenido en un volumen Ax₀ y tiene una temperatura T₀. Se libera el émbolo de masa m que representa el proyectil y el gas se expande. El gas (en color amarillo) a alta presión p y temperatura T, se comporta como un gas ideal. Su presión disminuye al aumentar el volumen V=Ax, siendo A el área de la sección transversal del tubo y x la posición del proyectil.

${\displaystyle pV=nRT,F=\frac{nRT}{x}}$

Supondremos que sobre el émbolo actúa únicamente la fuerza F=pA. Aplicamos la segunda ley de Newton para describir el movimiento del proyectil

${\displaystyle m\frac{d^{2}x}{d{t}^2}=\frac{nRT}{x}}$

El gas se expande adiabáticamente, de modo que su energía interna U=ncT disminuye a medida que realiza un trabajo, ncdT=-F·dx. c es el calor específico a volumen constante, 3R/2 para los gases monoatómicos y 5R/2 para los diatómicos.

${\displaystyle \begin{array}{l}nc·dT=-\frac{nRT}{x}dx\\ \ln \left(\frac{T}{T_0}\right)=-\frac{R}{c}\ln \left(\frac{x}{x_0}\right)\end{array}}$

Donde T₀ es la temperatura inicial del gas y Ax₀ el volumen inicial del gas

${\displaystyle T={\left(\frac{x_0}{x}\right)}^{R/c}{T}_0}$

Multiplicando por nR y teniendo en cuenta que el volumen V=Ax, obtenemos la relación entre presiones

${\displaystyle p={\left(\frac{x_0}{x}\right)}^{R/c+1}{p}_0}$

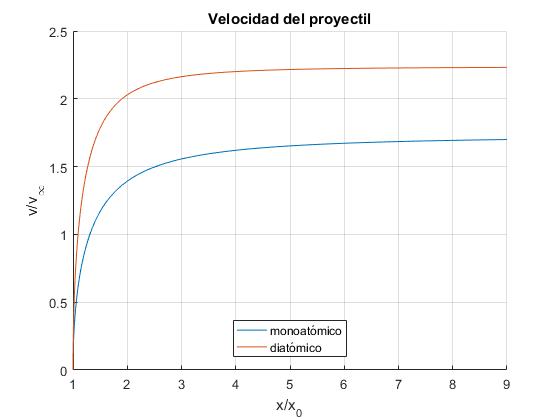
Velocidad del proyectil

Escribimos la ecuación diferencial del movimiento en otra equivalente de primer orden en v y x.

${\displaystyle v\frac{dv}{dx}=\frac{nR{T}_0{x}_0^{R/c}}{m}{x}^{-(R/c+1)}}$

Integramos la ecuación diferencial con la condición inicial: en la posición x₀ la velocidad inicial de la bala es v=0.

${\displaystyle v^2=\frac{2nc{T}_0}{m}\left(1-{\left(\frac{x_0}{x}\right)}^{R/c}\right)}$

Cuando x se hace grande, la velocidad tiende hacia un valor límite constante

${\displaystyle v_{\infty }=\sqrt{\frac{2nc{T}_0}{m}}}$

Supongamos un gas diatómico c=5R/2, cuya presión inicial p₀=10 atm, para que la presión se reduzca a p=1 atm.

${\displaystyle 1={\left(\frac{1}{z}\right)}^{7/5}10,z=\frac{x}{x_0}}$

z=5.2. Si n=0.1 moles de gas están a una temperatura inicial T₀=300 K, la masa del proyectil es m=0.1 kg, la velocidad v del proyectil es

${\displaystyle v^2=\frac{2·0.1·5·8.314·300}{2·0.1}\left(1-{5.2}^{-5/2}\right)}$

La velocidad del proyectil es v=110.7 m/s, cercana a la velocidad límite constante

hold on
fplot(@(z) sqrt(3*(1-z.^(-3/2))),[1,9])
fplot(@(z) sqrt(5*(1-z.^(-5/2))),[1,9])
hold off
grid on
xlabel('x/x_0')
ylabel('v/v_\infty')
legend('monoatómico','diatómico','location','south')
title('Velocidad del proyectil')

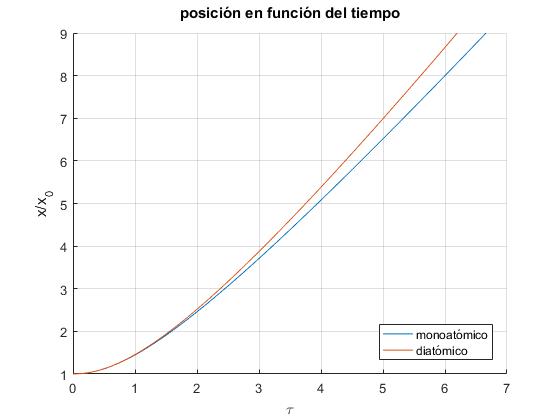
Posición del proyectil

Integramos de nuevo, para obtener la posición x de la bala en función del tiempo, t

${\displaystyle \begin{array}{l}\frac{dx}{dt}=\sqrt{\frac{2nc{T}_0}{m}}\sqrt{\left(1-{\left(\frac{x_0}{x}\right)}^{R/c}\right)}\\ {\displaystyle \underset{x_0}{\overset{x}{\int }}\frac{dx}{\sqrt{\left(1-{\left(\frac{x_0}{x}\right)}^{R/c}\right)}}}=\sqrt{\frac{2nc{T}_0}{m}}{\displaystyle \underset{0}{\overset{t}{\int }}dt}\end{array}}$

Esta integral se resuelve haciendo el cambio de variable

${\displaystyle \frac{x_0}{x}={\sin }^{2c/R}\theta }$

Con este cambio la integral se reduce a

${\displaystyle -\frac{2x_{0}c}{R}{\displaystyle \underset{\pi /2}{\overset{\phi }{\int }}\frac{d\theta }{{\sin }^{2c/R+1}\theta }}=\sqrt{\frac{2nc{T}_0}{m}}t,\sin \phi ={\left(\frac{x_0}{x}\right)}^{R/(2c)}}$

Resolveremos la integral para dos casos concretos: gas monoatómico c=3R/2 y gas diatómico c=5R/2

Gas monoatómico

${\displaystyle -3x_0{\displaystyle \underset{\pi /2}{\overset{\phi }{\int }}\frac{d\theta }{{\sin }^4\theta }}=\sqrt{\frac{3nR{T}_0}{m}}t,\sin \phi ={\left(\frac{x_0}{x}\right)}^{1/3}}$

La integración se realiza con el cambio de variable y la identidad siguientes:

${\displaystyle \begin{array}{l}y=\cot \theta 1+{\cot }^2\theta =\frac{1}{{\sin }^2\theta }\\ dy=-\frac{d\theta }{{\sin }^2\theta }\\ {\displaystyle \int \frac{d\theta }{{\sin }^4\theta }}=-{\displaystyle \int \frac{dy}{{\sin }^2\theta }}=-{\displaystyle \int \left(1+y^2\right)dy=-\left(y+\frac{y^3}{3}\right)}=-\cos \theta \frac{2{\sin }^2\theta +1}{3{\sin }^3\theta }\end{array}}$

Deshacemos los cambios

${\displaystyle \begin{array}{l}\cos \phi \frac{2{\sin }^2\phi +1}{{\sin }^3\phi }=\frac{1}{x_0}\sqrt{\frac{3nR{T}_0}{m}}t,\sin \phi ={\left(\frac{x_0}{x}\right)}^{1/3}\\ \sqrt{z^2-z^{4/3}}\left(2z^{1/3}+1\right)=\frac{1}{x_0}\sqrt{\frac{3nR{T}_0}{m}}t,z=\frac{x_0}{x}\\ \sqrt{z^2+3z^{4/3}-4}=\sqrt{3}\sqrt{\frac{nR{T}_0}{m{x}_0^2}}t\end{array}}$

Gas diatómico

${\displaystyle -5x_0{\displaystyle \underset{\pi /2}{\overset{\phi }{\int }}\frac{d\theta }{{\sin }^6\theta }}=\sqrt{\frac{5nR{T}_0}{m}}t,\sin \phi ={\left(\frac{x_0}{x}\right)}^{1/5}}$

La integración se realiza con el cambio de variable y la identidad siguientes:

${\displaystyle \begin{array}{l}y=\cot \theta 1+{\cot }^2\theta =\frac{1}{{\sin }^2\theta }\\ dy=-\frac{d\theta }{{\sin }^2\theta }\\ {\displaystyle \int \frac{d\theta }{{\sin }^6\theta }}=-{\displaystyle \int \frac{dy}{{\sin }^4\theta }}=-{\displaystyle \int {\left(1+y^2\right)}^{2}dy=-\left(y+\frac{2}{3}{y}^3+\frac{y^5}{5}\right)}=\\ -\cos \theta \frac{3+4{\sin }^2\theta +8{\sin }^4\theta }{15{\sin }^5\theta }\end{array}}$

Desahecemos los cambios

${\displaystyle \begin{array}{l}\cos \phi \frac{3+4{\sin }^2\phi +8{\sin }^4\phi }{3{\sin }^5\phi }=\frac{1}{x_0}\sqrt{\frac{5nR{T}_0}{m}}t,\sin \phi ={\left(\frac{x_0}{x}\right)}^{1/5}\\ \frac{1}{3}\sqrt{9z^2+15z^{8/5}+40z^{6/5}-64}=\sqrt{5}\sqrt{\frac{nR{T}_0}{m{x}_0^2}}t,z=\frac{x_0}{x}\end{array}}$

f=@(z) sqrt((z.^2+3*z.^(4/3)-4)/3);
g=@(z) sqrt((9*z.^2+15*z.^(8/5)+40*z.^(6/5)-64)/45);
hold on
fplot(f,[1,9])
fplot(g,[1,9])
hold off
grid on
legend('monoatómico','diatómico','location','southeast')
xlabel('x/x_0')
ylabel('\tau')
view([90 -90]) %intercambian los ejes X e Y
title('posición en función del tiempo')

Velocidad final del proyectil

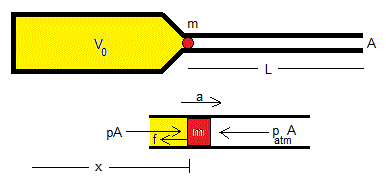
Consideremos un modelo de pistola de aire comprimido, consistente en un recipiente de volumen V₀ que contiene gas comprimido a la presión p₀. Un dispositivo libera el proyectil de masa m que se mueve a lo largo del tubo de longitud L y sección A.

Las fuerzas sobre el proyectil son:

• La fuerza que ejerce el gas comprimido, p·A, que va disminuyendo a medida que el gas se expande.
• La fuerza que ejerce la presión atmosférica, p_atm·A
• Una fuerza de fricción f entre el proyectil y las paredes del tubo.

La ecuación del movimiento del proyectil es:

${\displaystyle \begin{array}{l}m\frac{d^{2}x}{d{t}^2}=Ap-A{p}_{atm}-f\\ mv\frac{dv}{dx}=Ap-A{p}_{atm}-f\end{array}}$

A medida que se mueve el proyectil, el volumen del gas se incrementa V(x)=V₀+Ax

Transformación isoterma

Supondremos que la expansión es isotérmica: p(V₀+Ax)=p₀·V₀

Integramos para obtener la velocidad final v del proyectil cuando sale del tubo, x=L, sabiendo que en la posición inicial x=0, el proyectil parte del reposo, v=0

${\displaystyle v(L)=\sqrt{\frac{2}{m}\left(p_0{V}_0\ln \left(1+\frac{AL}{V_0}\right)-p_{atm}AL-fL\right)}}$

La velocidad del proyectil alcanza un máximo para la longitud del tubo L_max

${\displaystyle L_{\max }=\frac{V_0}{A}\left(\frac{p_{0}A}{p_{a}A+f}-1\right)}$

pa=1.013e5; %presión atmosférica
p0=200*pa; %presión inicial
V0=1.6e-5; %volumen inicial
A=1.6e-5; %sección del tubo
m=5.2e-4; %masa proyectil
f=0.5*p0*A; %fuerza de rozamiento

Lmax=V0*(p0*A/(pa*A+f)-1)/A
v=@(x) sqrt(2*(p0*V0*log(1+A*x/V0)-pa*A*x-f*x)/m);
fplot(v,[0,1.5*Lmax])
grid on
xlabel('L')
ylabel('v')
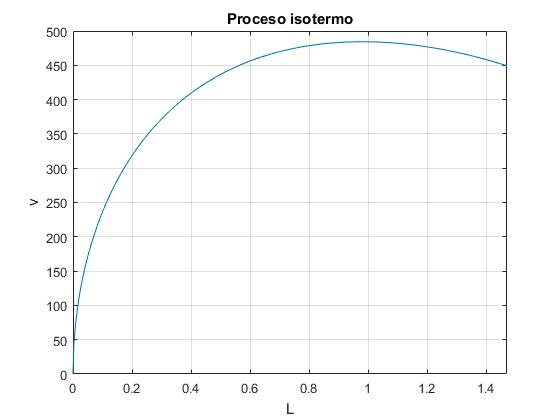
title('Proceso isotermo')

Lmax =    0.9802

Transformación adiabática

Si suponemos que la expansión es adiabática

${\displaystyle p{(V_0+Ax)}^{\gamma }=p_0{V}_0^{\gamma }}$

Integramos para obtener la velocidad final del proyectil cuando sale del tubo, x=L

${\displaystyle v(L)=\sqrt{\frac{2}{m}\left(\frac{p_0{V}_0}{\gamma -1}\left(1-{\left(\frac{V_0}{V_0+AL}\right)}^{\gamma -1}\right)-p_{atm}AL-fL\right)}}$

La velocidad v del proyectil alcanza un máximo para la longitud del tubo L_max

${\displaystyle L_{\max }=\frac{V_0}{A}\left({\left(\frac{p_{0}A}{p_{a}A+f}\right)}^{1/\gamma }-1\right)}$

pa=1.013e5; %presión atmosférica
p0=200*pa; %presión inicial
V0=1.6e-5; %volumen inicial
A=1.6e-5; %sección del tubo
m=5.2e-4; %masa proyectil
f=0.5*p0*A; %fuera de rozamiento
gamma=7/3; %gamma (gas diatómico)

Lmax=V0*((p0*A/(pa*A+f))^(1/gamma)-1)/A;
v=@(x) sqrt(2*((p0*V0/(gamma-1))*(1-(V0/(V0+A*x))^(gamma-1))-pa*A*x-f*x)/m);
fplot(v,[0,1.5*Lmax])
grid on
xlabel('L')
ylabel('v')
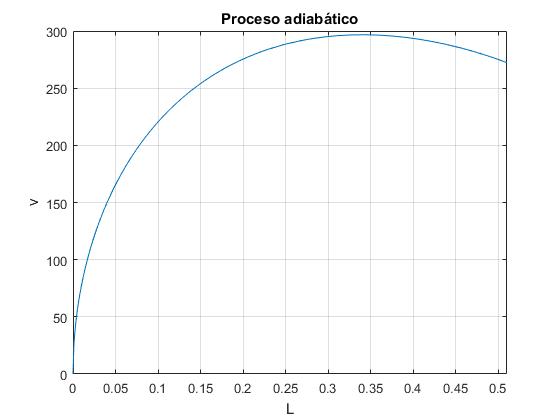
title('Proceso adiabático')

Lmax =    0.3402

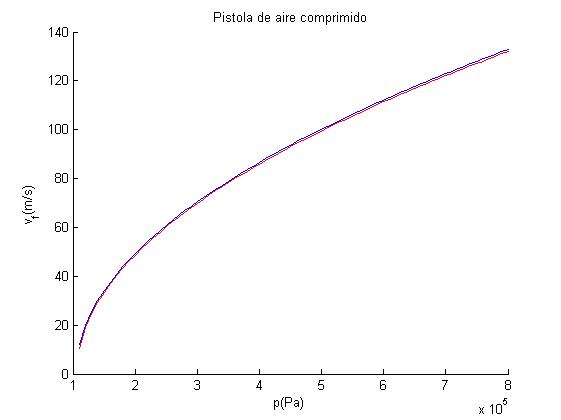
Comparación entre ambas transformaciones

Representamos la velocidad v del proyectil en función de la presión inicial p₀. Si no tenemos en cuenta la fuerza de rozamiento f. Veremos que no hay diferencia apreciable entre las velocidades finales del proyectil para un tubo de L=0.88 m de longitud

pAtm=101325; %Pa
m=19.4/1000; %kg
L=0.8825;
A=2.87233e-4; %m2
V0=4.196e-3; %volumen
gamma=1.4;
p0=110000:10000:800000;

vF=sqrt((p0*V0*(1-(V0/(A*L+V0))^(gamma-1))/(gamma-1)-A*L*pAtm)*2/m);
hold on
plot(p0,vF,'r')
vF=sqrt((p0*V0*log(1+A*L/V0)-A*L*pAtm)*2/m);
plot(p0,vF,'b')
hold off
xlabel('p(Pa)')
ylabel('v_f(m/s)')
title('Pistola de aire comprimido')

Movimiento del gas en el tubo

En la página, La fuerza que ejerce la presión atmosférica hemos tenido en cuenta el movimiento de la columna de aire a medida que la pelota se desplaza por el tubo. Se trata de un problema de masa variable

En este apartado no hemos tenido en cuenta que cuando el proyectil se ecuentra en la posición x a lo largo del tubo, una porción m_g de la masa M_g de gas se desplaza detrás del proyectil

${\displaystyle m_g(x)=\frac{Ax}{V_0+Ax}{M}_g{M}_g=\frac{p_0{V}_0}{R{T}_0}}$

La ecuación del movimiento se complicaría

${\displaystyle \frac{d\left((m+m_g)v\right)}{dt}=\left(p-p_{atm}\right)A-f}$

Referencias

Carl E Mungan. Internal ballistics of a pneumatic potato cannon. Eur. J. Phys. 30 (2009). pp. 453-457

Disponible en https://www.usna.edu/Users/physics/mungan/Publications/Publications.php#fndtn-panel120162017

Mark Denny. The Internal Balistics of an Air Gun. The Physics Teacher, Vol 49, February 2011, pp. 81-83

Z. J. Rohrbach, T. R. Buresh, M. J. Madsen. Modeling the exit velocity of a compressed air cannon Am. J. Phys. 80(1) January 2012, pp. 24-26