Ciclos térmicos

Primeras máquinas de vapor. Edimburgo, 7 de enero de 2017
Ciclo térmico de cuatro etapas
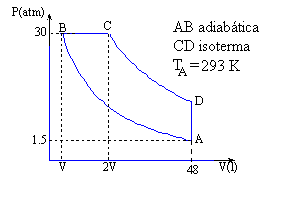
Una máquina térmica trabaja con 3 moles de un gas monoatómico, describiendo el ciclo reversible ABCD de la figura. Sabiendo que VC = 2 VB:
- Calcular el valor de las variables termodinámicas desconocidas en cada vértice.
- Deducir las expresiones del trabajo en cada etapa del ciclo.
- Calcular de forma directa en cada etapa del ciclo (siempre que sea posible), el trabajo, el calor, la variación de energía interna y la variación de entropía
- El rendimiento del ciclo.
R=0.082 atm·l/(mol·K) = J/(mol·K); 1cal=4.186 J; 1atm=1.013·105Pa, cv=3R/2
Índice adiabático
Presión, volumen y temperatura de los cuatro vétices
Vértice A. pA·VA=nRTA, 1.5·VA=3·0.082·293, VA=48.05 l
A→B, proceso adiabático.
Vértice B. pB·VB=nRTB, TB=971.1 K
Vértice C. pB·2VB=nRTC, TC=1942.3 K
C→D, proceso isotérmico. . pC·VC= pD·VD , pD =9.95 atm
| Vértice | p (atm) | V (l) | T (K) |
|---|---|---|---|
| A | 1.5 | 48.05 | 293 |
| B | 30 | 7.96 | 971.1 |
| C | 30 | 15.93 | 1942.3 |
| D | 9.95 | 48.05 | 1942.3 |
Variación de energía interna, calor, trabajo y variación de entropía
A→B, proceso adiabático
B→C, proceso isóbaro
C→D, proceso isotermo
D→A, proceso isócoro
QAB=0
WAB=- ΔUAB=--250.2 atm·l
Cálculo del trabajo de forma directa
Como vemos, WAB≈- ΔUAB
ΔSAB=0
Comprobación, ΔU≈Q-W
ΔUCD=0
Ciclo completo
| Proceso | ΔU (atm·l) | Q (atm·l) | W(atm·l) | ΔS (atm·l/K) |
|---|---|---|---|---|
| A→B | 250.2 | 0 | -250.2 | 0 |
| B→C | 358.4 | 597.3 | 239.1 | 0.43 |
| C→D | 0 | 527.5 | 527.5 | 0.27 |
| D→A | -608.6 | -608.6 | 0 | -0.70 |
| Total | 0 | 516.4 | 0 |
- Calor absorbido, Qabs=1124.8 atm·l
- Calor cedido, Qced=-608.6 atm·l
- Trabajo realizado, W=516.4 atm·l
Se cumple que, Qabs+Qced≈W
Rendimiento
%datos
pA=1.5;
vA=48;
TA=293;
pB=30;
pC=30;
R=0.082; %constante de los gases (atm·l)/(K·mol)
%gas monoatómico
gamma=5/3; % 7/5 para el diatómico
cV=3*R/2; %calor específico, 5*R/2 para el diatómico
%resultados
nMoles=pA*vA/(R*TA);
disp('Vértices');
%Proceso A-B
vB=(pA*vA^gamma/pB)^(1/gamma);
TB=(pB*vB)/(nMoles*R);
W_AB=-nMoles*cV*(TB-TA);
Q_AB=0;
%Proceso B-C
vC=2*vB;
TC=(pC*vC)/(nMoles*R);
W_BC=pB*(vC-vB);
Q_BC=nMoles*(cV+R)*(TC-TB);
%Proceso C-D
vD=vA;
TD=TC;
pD=(pC*vC)/vD;
W_CD=nMoles*R*TC*log(vD/vC);
Q_CD=W_CD;
%Proceso D-A
W_DA=0;
Q_DA=nMoles*cV*(TA-TD);
fprintf('Vertice A: pA=%2.2f, vA=%2.2f, TA=%2.2f\n', pA, vA, TA)
fprintf('Vertice B: pB=%2.2f, vB=%2.2f, TB=%2.2f\n', pB, vB, TB)
fprintf('Vertice C: pC=%2.2f, vC=%2.2f, TC=%2.2f\n', pC, vC, TC)
fprintf('Vertice D: pD=%2.2f, vD=%2.2f, TD=%2.2f\n', pD, vD, TD)
disp('Trabajo');
fprintf('W_AB=%2.2f, W_BC=%2.2f, W_CD=%2.2f, W_DA=%2.2f\n',
W_AB, W_BC, W_CD, W_DA)
disp('Calor');
fprintf('Q_AB=%2.2f, Q_BC=%2.2f, Q_CD=%2.2f, Q_DA=%2.2f\n',
Q_AB, Q_BC, Q_CD, Q_DA)
disp('Total')
W=W_AB+W_BC+W_CD+W_DA;
fprintf('Trabajo=%2.2f, Calor absorbido=%2.2f, Calor cedido=%2.2f\n',
W, Q_BC+Q_CD, Q_DA);
%gráfica del ciclo
hold on
v=linspace(vA,vB,50);
p=(pA*vA^gamma)./v.^gamma;
plot(v,p, 'r')
line([vB,vC],[pB,pC],'color','k')
v=linspace(vC,vD,50);
p=(nMoles*R*TC)./v;
plot(v,p, 'b')
line([vD,vA],[pD,pA],'color','k')
hold off
ylim([0,35]);
grid on
xlabel('v(l)')
ylabel('p(atm)')
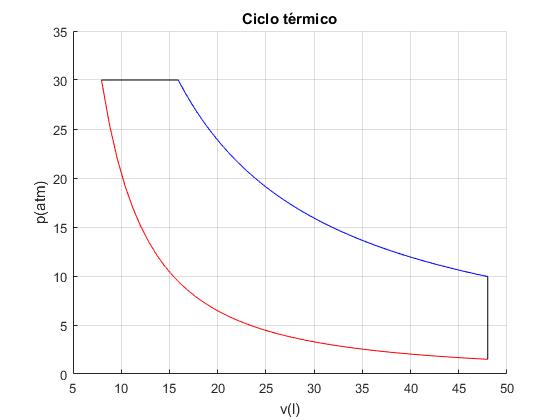
title('Ciclo térmico')
Vértices Vertice A: pA=1.50, vA=48.00, TA=293.00 Vertice B: pB=30.00, vB=7.95, TB=971.14 Vertice C: pC=30.00, vC=15.91, TC=1942.27 Vertice D: pD=9.94, vD=48.00, TD=1942.27 Trabajo W_AB=-249.96, W_BC=238.64, W_CD=527.06, W_DA=0.00 Calor Q_AB=0.00, Q_BC=596.60, Q_CD=527.06, Q_DA=-607.92 Total Trabajo=515.74, Calor absorbido=1123.66, Calor cedido=-607.92
Un ciclo de tres etapas
Vamos a calcular el rendimiento η de un ciclo térmico en función de r, cociente entre el volumen máximo y mínimo, y el indice adiabático γ de un gas
Primera variante
- La transformación 1→2 es adiabática
- La transformación 2→3 es isotérmica
- La transformación 3→1 es isócora (volumen constante)
Transformación adiabática, 1→2
Transformación isotérmica, 2→3
Transformación isocóra, 3→1
Calor absorbido en la etapa 3→1
Calor cedido en la etapa 2→3
Trabajo realizado, en las etapas 1→2 y 2→3
Rendimiento
Segunda variante
- La transformación 1→2 es isotérmica
- La transformación 2→3 es isócora (volumen constante)
- La transformación 3→1 es adiabática
Transformación isotérmica, 1→2
Transformación isócora, 2→3
Transformación adiabática, 3→1
Calor absorbido en la etapa 1→2
Calor cedido en la etapa 2→3
Trabajo realizado, en las etapas 1→2 y 3→1
Rendimiento
Tercera variante
- La transformación 1→2 es isóbara (presión constante)
- La transformación 2→3 es adiabática
- La transformación 3→1 es isotérmica
Transformación isóbara, 1→2
Transformación adiabática, 2→3
Transformación isotérmica, 3→1
Calor absorbido en la etapa 1→2
Calor cedido en la etapa 3→1
Trabajo realizado, en las etapas 1→3, 2→2 y 3→1
Rendimiento
Cuarta variante
- La transformación 1→2 es isotérmica
- La transformación 2→3 es isóbara (presión constante)
- La transformación 3→1 es adiabática
Transformación isotérmica, 1→2
Transformación isóbara, 2→3
Transformación adiabática, 3→1
Calor absorbido en la etapa 1→2
Calor cedido en la etapa 2→3
Trabajo realizado, en las etapas 1→2, 2→3 y 3→1
Rendimiento
Consideremos el siguiente ciclo de tres etapas
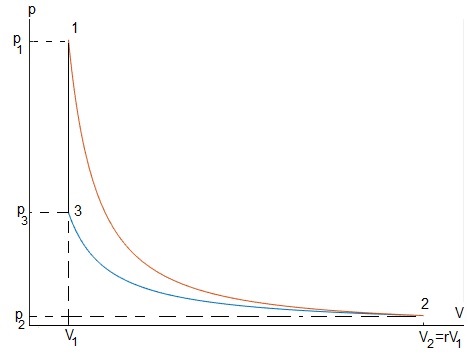
Sabiendo que el volumen máximo V2=r·V1. Calcular el calor absorbido, el cedido, el trabajo neto y el rendimiento η
Relación entre la presión p y el volumen V de los vértices
En una transformación adiabática, Q12=0
Trabajo
Relación entre la presión p y el volumen V de los vértices
El trabajo y calor son
W23<0, se realiza trabajo sobre el sistema que no cambia de energía interna por lo que cede una cantidad igual de calor Q23
Trabajo, no hay cambio de volumen, W31=0
Calor
Ciclo completo
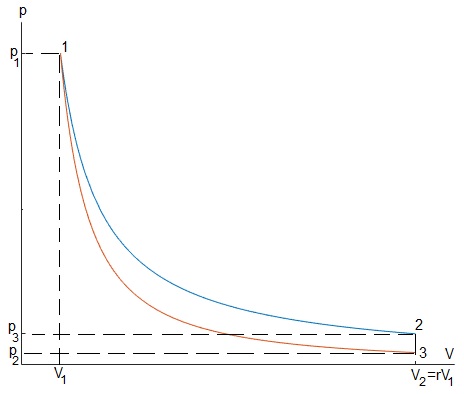
Sabiendo que el volumen máximo V2=r·V1. Calcular el calor absorbido, el cedido, el trabajo neto y el rendimiento η
Relación entre la presión p y el volumen V de los vértices
El trabajo y calor son
W12>0, el sistema realiza trabajo que no cambia la energía interna por lo que absorbe una cantidad igual de calor Q12
Trabajo, no hay cambio de volumen, W23=0
Calor
Relación entre la presión p y el volumen V de los vértices
En una transformación adiabática, Q31=0
Trabajo
Ciclo completo
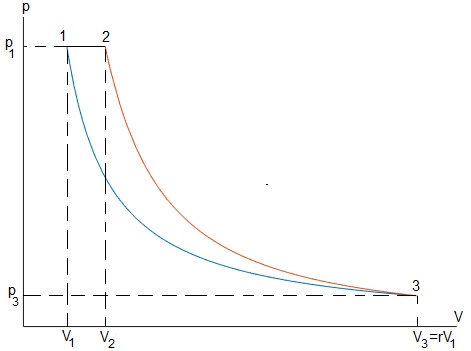
Sabiendo que el volumen máximo V3=r·V1. Calcular el calor absorbido, el cedido, el trabajo neto y el rendimiento η
Trabajo
Calor
Relación entre la presión p y el volumen V de los vértices
En una transformación adiabática, Q23=0
Trabajo
Relación entre la presión p y el volumen V de los vértices
El trabajo y calor son
W31<0, se realiza trabajo sobre el sistema que no cambia la energía interna por lo que cede una cantidad igual de calor Q31
Ciclo completo

Sabiendo que el volumen máximo V2=r·V1. Calcular el calor absorbido, el cedido, el trabajo neto y el rendimiento η
Relación entre la presión p y el volumen V de los vértices
Trabajo y calor
W12>0 el sistema realiza trabajo que no cambia de energía interna por lo que absorbe una cantidad igual de calor Q12
Trabajo
Calor
Relación entre la presión p y el volumen V de los vértices
En una transformación adiabática, Q31=0
Trabajo
Ciclo completo
Otro ciclo de tres etapas
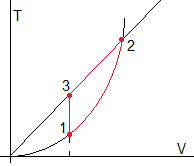
Un gas monoatómico (cv=3R/2, cp=5R/2) sigue el ciclo 1→2→3→1, mostrado en la figura.
- En el proceso 1→2 la temperatura y el volumen están relacionados por la ecuación T=bV2, donde b es constante.
- La temperatura T2 es cuatro veces mayor que T1
- Se sabe que el gas absorbe un calor Q en el proceso 1→2.
La solución es la siguiente
-
Proceso 1→2
-
Proceso 2→3
-
Proceso 3→1
Están en una línea recta
Volumen constante
El resultado se muestra en la figura más abajo
Trabajo, calor y variación de energía interna
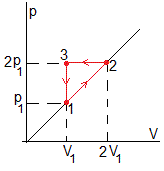
-
Proceso 1→2
-
Proceso 2→3
-
Proceso 3→1
El calor en este proceso es un dato del problema, Q1→2
Trabajo
La presión es constante, el trabajo es
El volumen es constante
El trabajo total es negativo y es el área del triángulo p1V1/2
El calor total es
En un ciclo completo
Otra forma
El calor cedido es 13nRT1/2
Variación de entropía
-
Proceso 1→2
-
Proceso 2→3
-
Proceso 3→1
La variación de entropía en el ciclo completo es cero
Una máquina térmica que no produce trabajo neto
En esta sección estudiamos un curioso ciclo térmico
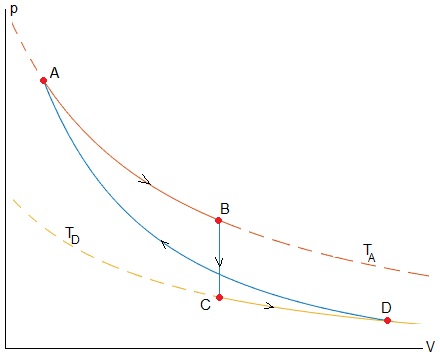
Un gas monoatómico describe el ciclo de la figura que consta de los siguientes procesos
- AB, es isotermo a la temperatura TA
- BC, isócoro, a volumen constante VB
- CD, es isotermo a la temperatura TD
- DA, adibático
Sea pA=3 atm, VA=2 l, TA=600 K, TD=300 K
El volumen VB=VC se determina del siguiente modo: El trabajo producido en las expansiones isotérmicas a temperatura TA y TD se invierte en la compresión adibática. El trabajo neto es cero.
De momento, asignaremos a VB=(VA+VD)/2
Presión, volumen y temperatura de los cuatro vétices
pAVA=nR·TA, nR=1/100
pDVD=nR·TD, pDVD=3
De la ecuación de la adibática obtenemos la presión pD y el volumen VD
Sea el volumen VB=(VA+VD)/2=3.8285 l
pBVB=nR·TA, pB=6/VB=1.5672 atm
pCVC=nR·TD, pC=3/VC=0.7836 atm
| Vértice | p (atm) | V (l) | T (K) |
|---|---|---|---|
| A | 3 | 2 | 600 |
| B | 1.5672 | 3.8285 | 600 |
| C | 0.7836 | 3.8285 | 300 |
| D | 0.5303 | 5.6569 | 300 |
Variación de energía interna, calor, trabajo y variación de entropía
A→B, proceso isotermo a la temperatura TA
B→C, proceso isócoro
C→D, proceso isotermo a la temperatura TD
D→A, proceso adiabático
El trabajo se puede calcular de forma directa
Ciclo completo
| Proceso | ΔU (atm·l) | Q (atm·l) | W(atm·l) | ΔS (atm·l/K) |
|---|---|---|---|---|
| A→B | 0 | 3.8958 | 3.8958 | 0.0065 |
| B→C | -4.5 | -4.5 | 0 | -0.0104 |
| C→D | 0 | 1.1712 | 1.1712 | 0.0039 |
| D→A | 4.5 | 0 | -4.5 | 0 |
| Total | 0 | 0.5670 | 0 |
- Calor absorbido, Qabs=5.0670 atm·l
- Calor cedido, Qced=4.5 atm·l
- Trabajo realizado, W=0.5670 atm·l
Se cumple que, Qabs+Qced≈W
Rendimiento
%datos
pA=3;
vA=2;
TA=600;
TD=300;
%gas monoatómico
gamma=5/3;
cV=3/2;
%resultados
nR=pA*vA/TA;
vD=(pA*vA^gamma/(nR*TD))^(1/(gamma-1));
pD=nR*TD/vD;
vB=(vA+vD)/2; %3.1690;
pB=nR*TA/vB;
vC=vB;
pC=nR*TD/vC;
%Proceso A-B
W_AB=nR*TA*log(vB/vA);
Q_AB=W_AB;
%Proceso B-C
W_BC=0;
Q_BC=nR*cV*(TD-TA);
%Proceso C-D
W_CD=nR*TD*log(vD/vC);
Q_CD=W_CD;
%Proceso D-A
W_DA=nR*cV*(TD-TA);
Q_DA=0;
fprintf('Vertice A: pA=%2.2f, vA=%2.2f, TA=%2.2f\n', pA, vA, TA)
fprintf('Vertice B: pB=%2.2f, vB=%2.2f, TB=%2.2f\n', pB, vB, TA)
fprintf('Vertice C: pC=%2.2f, vC=%2.2f, TC=%2.2f\n', pC, vC, TD)
fprintf('Vertice D: pD=%2.2f, vD=%2.2f, TD=%2.2f\n', pD, vD, TD)
disp('Trabajo');
fprintf('W_AB=%2.2f, W_BC=%2.2f, W_CD=%2.2f, W_DA=%2.2f\n', W_AB, W_BC, W_CD, W_DA)
disp('Calor');
fprintf('Q_AB=%2.2f, Q_BC=%2.2f, Q_CD=%2.2f, Q_DA=%2.2f\n', Q_AB, Q_BC, Q_CD, Q_DA)
disp('Total')
W=W_AB+W_BC+W_CD+W_DA;
fprintf('Trabajo=%2.2f, Calor absorbido=%2.2f, Calor cedido=%2.2f\n',
W, Q_AB+Q_CD, Q_BC);
%gráfica del ciclo
hold on
p=@(x) (pA*vA^gamma)./x.^gamma;
fplot(p,[vA,vD])
p1=@(x) pA*vA./x;
fplot(p1,[vA,vB])
p2=@(x) pD*vD./x;
fplot(p2,[vC,vD])
line([vB, vB],[p1(vB),p2(vB)])
hold off
grid on
xlabel('v(l)')
ylabel('p(atm)')
title('Ciclo térmico')
Vertice A: pA=3.00, vA=2.00, TA=600.00 Vertice B: pB=1.57, vB=3.83, TB=600.00 Vertice C: pC=0.78, vC=3.83, TC=300.00 Vertice D: pD=0.53, vD=5.66, TD=300.00 Trabajo W_AB=3.90, W_BC=0.00, W_CD=1.17, W_DA=-4.50 Calor Q_AB=3.90, Q_BC=-4.50, Q_CD=1.17, Q_DA=0.00 Total Trabajo=0.57, Calor absorbido=5.07, Calor cedido=-4.50
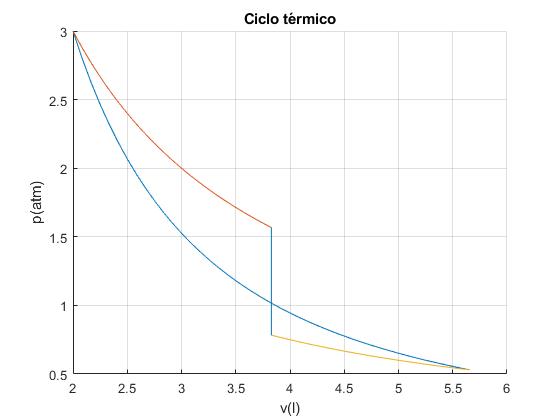
Trabajo neto nulo
Cuando el trabajo a lo largo de las dos isotermas AB y CD es igual al trabajo en el proceso adiabático DA, el trabajo total es cero. Hemos creado un motor térmico que describe un ciclo que no sirve para nada
El volumen VB=VC=3.1690 l
En el script asignamos a la variable
Una variante de este ciclo
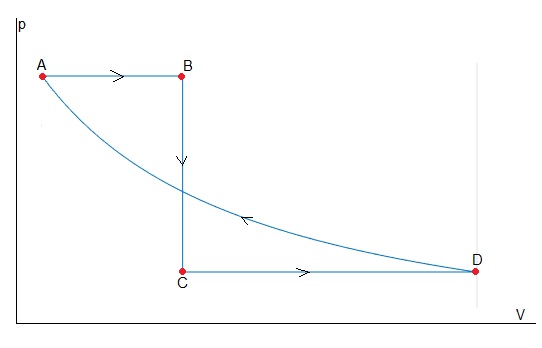
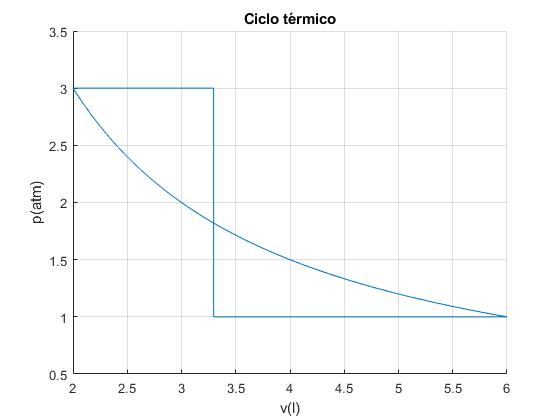
Un gas monoatómico describe el ciclo de la figura que consta de los siguientes procesos:
- AB, es isóbaro a la presión pA
- BC, isócoro, a volumen constante VB
- CD, es isóbaro a la presión pD
- DA, isotermo a la temperatura T=TA=TD
Sea pA=3 atm, VA=2 l, TA=600 K
En el proceso isotermo AD se cumple que pAVA=pDVD=nR·T
El volumen VB, se determina, igualando el trabajo en las expansiones isóbaras AB y CD con el trabajo para comprimir el gas isotérmicamente en el proceso DA. El trabajo neto es cero
Cuando existe una relación entre los volúmenes, VA, VD y VB, no se produce trabajo neto
%datos
pA=3;
vA=2;
vD=6;
TA=600;
TD=600;
cV=3/2;
cP=5/2;
%resultados
nR=pA*vA/TA;
pD=pA*vA/vD;
pB=pA;
pC=pD;
vB=pA*vA*log(vD/vA)/(pA-pD);
vC=vB;
TB=pB*vB/nR;
TC=pC*vC/nR;
%Proceso A-B
W_AB=pA*(vB-vA);
Q_AB=cP*nR*(TB-TA);
%Proceso B-C
W_BC=0;
Q_BC=cV*nR*(TC-TB);
%Proceso C-D
W_CD=pC*(vD-vC);
Q_CD=cP*nR*(TD-TC);
%Proceso D-A
W_DA=nR*T*log(vA/vD);
Q_DA=W_DA;
fprintf('Vertice A: pA=%2.2f, vA=%2.2f, TA=%2.2f\n', pA, vA, TA)
fprintf('Vertice B: pB=%2.2f, vB=%2.2f, TB=%2.2f\n', pB, vB, TB)
fprintf('Vertice C: pC=%2.2f, vC=%2.2f, TC=%2.2f\n', pC, vC, TC)
fprintf('Vertice D: pD=%2.2f, vD=%2.2f, TD=%2.2f\n', pD, vD, TD)
disp('Trabajo');
fprintf('W_AB=%2.2f, W_BC=%2.2f, W_CD=%2.2f, W_DA=%2.2f\n', W_AB, W_BC, W_CD, W_DA)
disp('Calor');
fprintf('Q_AB=%2.2f, Q_BC=%2.2f, Q_CD=%2.2f, Q_DA=%2.2f\n', Q_AB, Q_BC, Q_CD, Q_DA)
disp('Total')
W=W_AB+W_BC+W_CD+W_DA;
fprintf('Trabajo=%2.2f, Calor absorbido=%2.2f, Calor cedido=%2.2f\n',
W, Q_AB+Q_CD, Q_BC+Q_DA);
%gráfica del ciclo
hold on
p=@(x) pA*vA./x;
fplot(p,[vA,vD])
line([vA, vB],[pA,pA])
line([vB, vB],[pA,pD])
line([vB, vD],[pD,pD])
hold off
ylim([0.5,3.5])
grid on
xlabel('v(l)')
ylabel('p(atm)')
title('Ciclo térmico')
Vertice A: pA=3.00, vA=2.00, TA=600.00 Vertice B: pB=3.00, vB=3.30, TB=988.75 Vertice C: pC=1.00, vC=3.30, TC=329.58 Vertice D: pD=1.00, vD=6.00, TD=600.00 Trabajo W_AB=3.89, W_BC=0.00, W_CD=2.70, W_DA=-6.59 Calor Q_AB=9.72, Q_BC=-9.89, Q_CD=6.76, Q_DA=-6.59 Total Trabajo=-0.00, Calor absorbido=16.48, Calor cedido=-16.48
Referencias
Tiago Kroetz. Thermal efficiency and work output in four three-stage heat engine models. Revista Brasileira de Ensino de Física, vol. 47, e20250137 (2025)
Physics Challenge for Teachers and Students. Solution to January 2008 Challenge. The Physics Teacher, 48 January 2008, pp. 496-498
P.-M. Binder, C. K. S. Tanoue. Variations on the Zilch Cycle. The Physics Teacher, Vol. 51, October 2013, pp. 434-436

