Un ciclo térmico poco habitual (Sadly Cannot)

Estudiamos en esta página, un ciclo térmico poco habitual denominado 'Sadly cannot' que consta de dos procesos: una expansión lineal desde el estado (p₁, V₁, T₁) al estado (p₂, V₂, T₂) seguida una compresión adiabática desde el estado 2 al 1.

Representamos gráficamente el ciclo, con los siguientes datos, p₁=32 Pa, V₁=8 m³, V₂=64 m³. Para un gas monoatómico, γ=5/3.

Obtenemos la presión p₂ por medio de la ecuación de la adiabática

$p_{1} V_{1}^{γ} = p_{2} V_{2}^{γ}$

p₂=32·(8/64)^5/3=1

p1=32;
V1=8;
V2=64;
gamma=5/3; %monoatómico
p2=p1*(V1/V2)^gamma;
hold on
fplot(@(x) p1*V1^gamma./x.^gamma,[V1,V2])
plot(V1,p1,'ro','markersize',3,'markerfacecolor','r')
plot(V2,p2,'ro','markersize',3,'markerfacecolor','r')
line([V1,V2],[p1,p2])
hold off
grid on
xlabel('v (m^3)')
ylabel('p (Pa)')
title('Ciclo térmico')

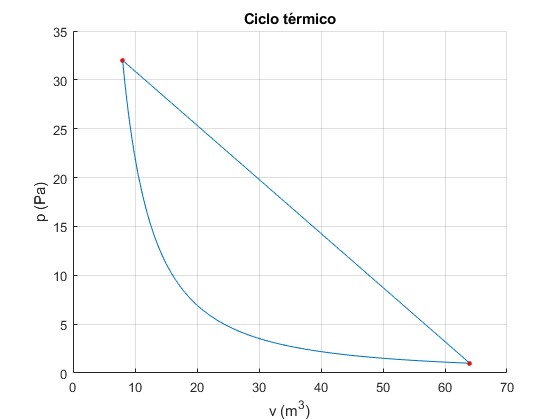
La ecuación del proceso lineal es p=aV+b, despejamos la pendiente a y la ordenada en el origen b en el sistema de dos ecuaciones

$\begin{array}{l} {\begin{cases} p_{1} = a V_{1} + b \\ p_{2} = a V_{2} + b \end{cases} \\ a = \frac{p_{2} - p_{1}}{V_{2} - V_{1}}, b = \frac{p_{1} V_{2} - p_{2} V_{1}}{V_{2} - V_{1}} \\ a = - \frac{31}{56}, b = \frac{255}{7} \end{array}$

Análisis habitual, erróneo

Proceso lineal, 1→2

Trabajo

$W_{1 - 2} = \int_{V_{1}}^{V_{2}} p \cdot d V = \int_{V_{1}}^{V_{2}} (a V + b) \cdot d V = {\frac{1}{2} a V^{2} + b V |}_{V_{1}}^{V_{2}} = 924 J$

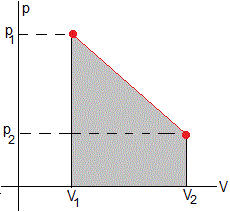
El trabajo es el área sombreada de color gris claro

$\begin{array}{l} W_{1 - 2} = p_{2} (V_{2} - V_{1}) + \frac{1}{2} (p_{2} - p_{1}) (V_{2} - V_{1}) = \\ \frac{1}{2} (p_{1} + p_{2}) (V_{2} - V_{1}) = 924 J \end{array}$

La variación de energía interna es

$\begin{array}{l} Δ U_{1 - 2} = \frac{3}{2} n R (T_{2} - T_{1}) = \\ \frac{3}{2} (p_{2} V_{2} - p_{1} V_{1}) = - 288 J \end{array}$

Aplicando el primer principio obtenemos el calor

$\begin{array}{l} Δ U = Q - W \\ Q_{1 - 2} = Δ U_{1 - 2} + W_{1 - 2} = - 288 + 924 = 636 J \end{array}$

Proceso adiabático, 2→1

El trabajo en un proceso adiabático es

$W_{2 - 1} = \frac{1}{- γ + 1} (p_{1} V_{1} - p_{2} V_{2}) = - 288 J$

La variación de energía interna

$Δ U_{2 - 1} = \frac{3}{2} n R (T_{1} - T_{2}) = \frac{3}{2} (p_{1} V_{1} - p_{2} V_{2}) = 288 J$

En un proceso adiabático no hay intercambio de calor

$Q_{2 - 1} = 0$

El trabajo neto es, W=636 J

El calor absorbido, Q_abs=636 J

El rendimiento

$η = \frac{W}{Q_{a b s}} = \frac{636}{636} = 1$

Este rendimiento no es posible, por lo que se precisa un estudio más detallado del problema

Análisis detallado

En el proceso lineal 1→2 hay un estado (p_m, V_m, T_m), tal que p_m=aV_m+b para el cual el flujo de calor cambia de sentido. Este punto donde Q=0 es tangente a una adiabática pV^γ=cte. La pendiente de la adiabática en (p_m, V_m) es a

p1=32;
V1=8;
V2=64;
gamma=5/3; %monoatómico
p2=p1*(V1/V2)^gamma;
hold on
fplot(@(x) p1*V1^gamma./x.^gamma,[V1,V2])
plot(V1,p1,'ro','markersize',3,'markerfacecolor','r')
plot(V2,p2,'ro','markersize',3,'markerfacecolor','r')
line([V1,V2],[p1,p2])
a=(p2-p1)/(V2-V1);
b=(p1*V2-p2*V1)/(V2-V1);
Vm=-gamma*b/(a*(1+gamma));
pm=b/(1+gamma);
fplot(@(x) pm*Vm^gamma./x.^gamma,[30,60])
plot(Vm,pm,'bo','markersize',3,'markerfacecolor','b')
hold off
grid on
xlabel('v (m^3)')
ylabel('p (Pa)')
title('Ciclo térmico')

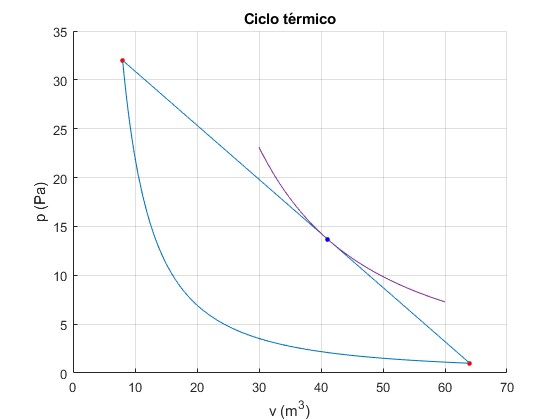
$\begin{array}{l} p V^{γ} = cte \\ \frac{d p}{d V} = - cte \frac{γ}{V^{γ + 1}} = - p V^{γ} \frac{γ}{V^{γ + 1}} = - \frac{γ p}{V} \\ {\frac{d p}{d V} |}_{m} = - \frac{γ p_{m}}{V_{m}} = a \end{array}$

Conocidos a y b despejamos p_m y V_m.

$\begin{array}{l} V_{m} = - \frac{γ b}{a (1 + γ)} = - \frac{5 b}{8 a} = \frac{1275}{31} m^{3} \\ p_{m} = \frac{b}{1 + γ} = \frac{3 b}{8} = \frac{765}{56} Pa \end{array}$

Subproceso 1→m

Variación de energía interna

$Δ U_{1 - m} = \frac{3}{2} n R (T_{m} - T_{1}) = \frac{3}{2} (p_{m} V_{m} - p_{1} V_{1}) = 458.8 J$

Trabajo

$W_{1 - m} = \int_{V_{1}}^{V_{m}} p \cdot d V = \int_{V_{1}}^{V_{m}} (a V + b) \cdot d V = {\frac{1}{2} a V^{2} + b V |}_{V_{1}}^{V m} = 756.3 J$

Aplicando el primer principio obtenemos el calor absorbido

$Q_{1 - m} = Δ U_{1 - m} + W_{1 - m} = 1215.1 J$

Subproceso m→2

Variación de energía interna

$Δ U_{m - 2} = \frac{3}{2} n R (T_{2} - T_{m}) = \frac{3}{2} (p_{2} V_{2} - p_{m} V_{m}) = - 746.8 J$

Trabajo

$W_{m - 2} = \int_{V_{m}}^{V_{2}} p \cdot d V = \int_{V_{m}}^{V_{2}} (a V + b) \cdot d V = {\frac{1}{2} a V^{2} + b V |}_{V_{m}}^{V 2} = 167.6 J$

Aplicando el primer principio obtenemos el calor cedido

$Q_{m - 2} = Δ U_{m - 2} + W_{m - 2} = - 579.1 J$

Proceso lineal 1→2

Variación de energía interna

$Δ U_{1 - 2} = Δ U_{1 - m} + Δ U_{m - 2} = - 288 J$

Trabajo

$W_{1 - 2} = W_{1 - m} + W_{m - 2} = 924 J$

El calor

$Q_{1 - 2} = Q_{1 - m} + Q_{m - 2} = 636 J$

Q_1-2 no es el calor absorbido, sino Q_1-m

Ciclo completo

Trabajo neto W=636 J

Calor absorbido, Q_abs=1215.1 J

Rendimiento

$η = \frac{W}{Q_{a b s}} = \frac{636}{1215.1} = 0.52$

Temperatura máxima

En el proceso lineal 1→2 hay un estado (p_h, V_h, T_h), tal que p_h=aV_h+b para el cual, la temperatura es máxima. Este punto es tangente a una isoterma pV=cte. La pendiente de la isoterma en (p_h, V_h) es a

$\begin{array}{l} p V = cte \\ \frac{d p}{d V} = - \frac{cte}{V^{2}} = - \frac{p V}{V^{2}} = - \frac{p}{V} \\ {\frac{d p}{d V} |}_{h} = - \frac{p_{h}}{V_{h}} = a \end{array}$

Conocidos a y b despejamos p_h y V_h.

$\begin{array}{l} V_{h} = - \frac{b}{2 a} = \frac{1020}{31} m^{3} \\ p_{h} = \frac{b}{2} = \frac{255}{14} Pa \end{array}$

p1=32;
V1=8;
V2=64;
gamma=5/3; %monoatómico
p2=p1*(V1/V2)^gamma;
hold on
fplot(@(x) p1*V1^gamma./x.^gamma,[V1,V2])
plot(V1,p1,'ro','markersize',3,'markerfacecolor','r')
plot(V2,p2,'ro','markersize',3,'markerfacecolor','r')
line([V1,V2],[p1,p2])
a=(p2-p1)/(V2-V1);
b=(p1*V2-p2*V1)/(V2-V1);
ph=b/2;
Vh=-b/(2*a);
fplot(@(x) ph*Vh./x,[20,60])
plot(Vh,ph,'bo','markersize',3,'markerfacecolor','b')

hold off
grid on
xlabel('v (m^3)')
ylabel('p (Pa)')
title('Ciclo térmico')

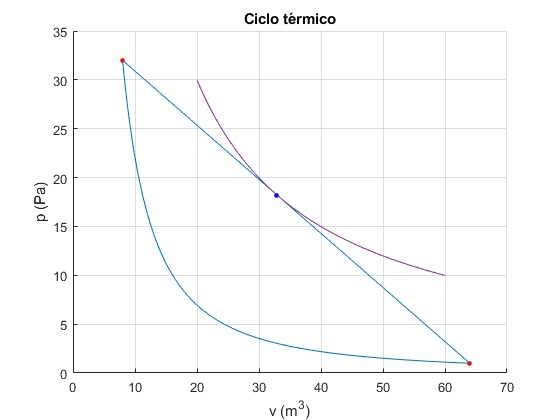
Otra forma de obtener el estado (p_h, V_h, T_h), es la siguiente

La temperatura de cada uno de los estados a lo largo del proceso lineal 1→2 es

$\begin{array}{l} p V = n R T \\ T = \frac{(a V + b) V}{n R} \end{array}$

La temperatrura máxima T_h es el extremo

$\begin{array}{l} \frac{d T}{d V} = 0 \\ 2 a V_{h} + b = 0 \\ V_{h} = - \frac{b}{2 a}, p_{h} = a V_{h} + b = \frac{b}{2} \end{array}$

Un ciclo de Carnot que operase entre dos focos uno a la temperatura T₂ y otro a la temperatura T_h, su rendimiento sería

$η = 1 - \frac{T_{2}}{T_{h}} = 1 - \frac{n R T_{2}}{n R T_{h}} = 1 - \frac{p_{2} V_{2}}{p_{h} V_{h}} = 0.89$

Trabajo, calor absorbido y rendimiento del ciclo

En este apartado expresamos el trabajo, el calor absorbido y el rendimiento de ciclo en función del cociente entre volúmenes, r=V₂/V₁.

En el proceso lineal, p=aV+b

$\begin{array}{l} {\begin{cases} p_{1} = a V_{1} + b \\ p_{2} = a V_{2} + b \end{cases} \\ a = \frac{p_{2} - p_{1}}{V_{2} - V_{1}} = \frac{p_{1} {(\frac{V_{1}}{V_{2}})}^{γ} - p_{1}}{V_{2} - V_{1}} = \frac{p_{1}}{V_{1}} \frac{r^{- γ} - 1}{r - 1} = \frac{p_{1}}{V_{1}} α, α = \frac{r^{- γ} - 1}{r - 1} \\ b = p_{1} (1 - α) \end{array}$

El trabajo neto es la suma de dos contribuciones, el trabajo en el proceso lineal y en el proceso adiabático

$\begin{array}{l} W = W_{1 - 2} + W_{2 - 1} = \frac{1}{2} (p_{1} + p_{2}) (V_{2} - V_{1}) + \frac{1}{- γ + 1} (p_{1} V_{1} - p_{2} V_{2}) = \\ \frac{1}{2} (p_{1} + p_{1} {(\frac{V_{1}}{V_{2}})}^{γ}) (V_{2} - V_{1}) + \frac{1}{- γ + 1} (p_{1} V_{1} - p_{1} {(\frac{V_{1}}{V_{2}})}^{γ} V_{2}) = \\ p_{1} V_{1} {\frac{1}{2} (1 + r^{- γ}) (r - 1) + \frac{1}{- γ + 1} (1 - r^{1 - γ})} \end{array}$

Para un gas monoatómico γ=5/3

$W = \frac{p_{1} V_{1}}{2} (r + 4 r^{- 2 / 3} - r^{- 5 / 3} - 4)$

Los resultados que obtuvimos en el apartado anterior

$\begin{array}{l} V_{m} = - \frac{γ b}{a (1 + γ)}, p_{m} = \frac{b}{1 + γ} \\ a = \frac{p_{1}}{V_{1}} α, b = p_{1} (1 - α) \\ V_{m} = - V_{1} \frac{γ (1 - α)}{α (1 + γ)}, p_{m} = p_{1} \frac{1 - α}{1 + γ} \end{array}$

Para un gas monoatómico γ=5/3

$V_{m} = - V_{1} \frac{5 (1 - α)}{8 α}, p_{m} = p_{1} \frac{3 (1 - α)}{8}$

El calor absorbido es la suma de la variación de energía interna y del trabajo en el subproceso lineal 1→m

$\begin{array}{l} Q_{a b s} = Q_{1 - m} = Δ U_{1 - m} + W_{1 - m} = \frac{3}{2} (p_{m} V_{m} - p_{1} V_{1}) + \int_{V_{1}}^{V_{m}} (a V + b) \cdot d V = \\ \frac{3}{2} (p_{m} V_{m} - p_{1} V_{1}) + \frac{1}{2} a (V_{m}^{2} - V_{1}^{2}) + b (V_{m} - V_{1}) = \\ \frac{3}{2} (p_{m} V_{m} - p_{1} V_{1}) + (V_{m} - V_{1}) {\frac{1}{2} a (V_{m} + V_{1}) + b} = \\ - p_{1} V_{1} {\frac{3}{2} (\frac{{(1 - α)}^{2} γ}{{(1 + γ)}^{2} α} + 1) + (\frac{(1 - α) γ}{(1 + γ) α} + 1) {\frac{α}{2} (1 - \frac{(1 - α) γ}{(1 + γ) α}) + 1 - α}} = \\ - p_{1} V_{1} {\frac{3}{2} (\frac{{(1 - α)}^{2} γ}{{(1 + γ)}^{2} α} + 1) + (\frac{(1 - α) γ}{(1 + γ) α} + 1) {1 - \frac{α}{2} - \frac{(1 - α) γ}{2 (1 + γ)}}} = \\ - p_{1} V_{1} {\frac{3}{2} \frac{{(1 - α)}^{2} γ}{{(1 + γ)}^{2} α} + \frac{3}{2} + \frac{(1 - α) γ}{(1 + γ) α} - \frac{(1 - α) γ}{2 (1 + γ)} - \frac{{(1 - α)}^{2} γ^{2}}{2 {(1 + γ)}^{2} α} + 1 - \frac{α}{2} - \frac{(1 - α) γ}{2 (1 + γ)}} = \\ - p_{1} V_{1} {\frac{5}{2} - \frac{α}{2} + \frac{{(1 - α)}^{2} γ}{2 α {(1 + γ)}^{2}} (3 - γ) + \frac{{(1 - α)}^{2} γ}{(1 + γ) α}} \end{array}$

Para un gas monoatómico γ=5/3

$Q_{a b s} = - p_{1} V_{1} \frac{9 α^{2} + 30 α + 25}{32 α}, α = \frac{r^{- 5 / 3} - 1}{r - 1}$

El rendimiento es

$η = \frac{W}{Q_{a b s}} = - \frac{16 (r^{- 5 / 3} - 1) (r - 1) (r + 4 r^{- 2 / 3} - r^{- 5 / 3} - 4)}{9 {(r^{- 5 / 3} - 1)}^{2} + 30 (r^{- 5 / 3} - 1) (r - 1) + 25 {(r - 1)}^{2}}$

Cuando r=V₂/V₁ se hace muy grande, el rendimiento η tiende a

$\lim_{r \to \infty} η (r) = \frac{16}{25} = 0.64$

>> syms r;
>> y=-16*(r^(-5/3)-1)*(r-1)*(r+4*r^(-2/3)-r^(-5/3)-4)/(9*(r^(-5/3)-1)^2+
30*(r^(-5/3)-1)*(r-1)+25*(r-1)^2);
>> limit(y,r,inf)
ans =16/25

Representamos el rendimiento η en función de r=V₂/V₁, a partir del valor de r en el que el cociente W/Q_abs se hace positivo

Obtenemos este valor inicial de r, utilizando la función fzero de MATLAB

p1=32;
V1=8;
V2=64;
W=@(r) p1*V1*(r+4*r.^(-2/3)-r.^(-5/3)-4)/2;
alfa=@(r) (r.^(-5/3)-1)./(r-1);
Q=@(r)-p1*V1*(9*alfa(r).^2+30*alfa(r)+25)./(32*alfa(r));
f=@(r) W(r)./Q(r);
rIni=fzero(f,[0.1,5]);
fplot(f,[rIni,25])
r=V2/V1;
rendimiento=f(r);
line([r,r],[0,rendimiento], 'lineStyle','--')
line([0,r],[rendimiento,rendimiento], 'lineStyle','--')
grid on
xlabel('r')
ylabel('\eta')
title('Rendimiento')

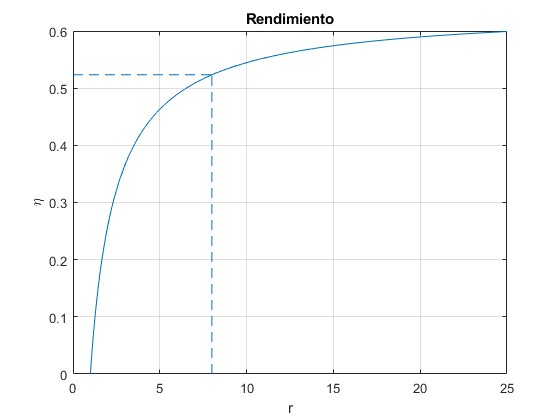
En la gráfica, señalamos el valor de r=V₂/V₁=64/8=8, del ciclo estudiado en el primer apartado, el rendimiento obtenido, η=0.52

Referencias

J. Willis, D. F. Kirwan. The ‘Sadly Cannot’ thermodynamic cycle. Phys. Teach. 18, pp. 51–52 (1980)

D. S. Mills, C. S. Huston, The ‘Sadly Cannot’ thermodynamic cycle revisited, Phys. Teach. 29, pp. 180–181 (1991).

Bruce Cameron Reed. A Deeper Look at the Sadly Cannot Thermodynamic Cycle. the Physics Teacher Vol. 61, May 2023, pp. 331-333