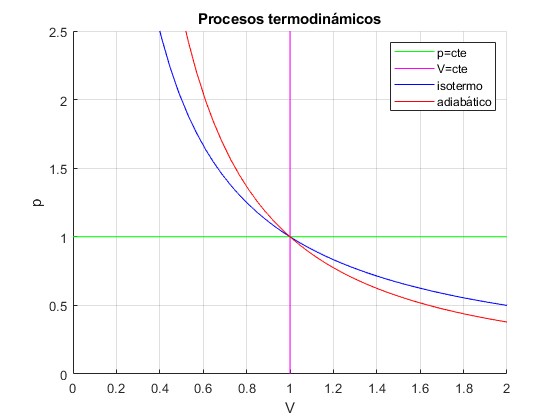
Representamos los cuatro procesos termodinámicos

hold on
line([0,2],[1,1], 'color', 'g')
line([1,1],[0,2.5],'color','m')
fplot(@(V) 1./V,[0.25,2], 'color','b')
fplot(@(V) 1./V.^1.4,[0.25,2], 'color','r')
hold off
grid on
ylim([0,2.5])
xlabel('V')
legend('p=cte','V=cte','isotermo','adiabático')
ylabel ('p')
title('Procesos termodinámicos')

Conocida la relación entre presión y volumen en un proceso politrópico, pV^β=cte, para un gas ideal cuya ecuación de estado es pV=nRT

• La relación entre volumen V y temperatura T es

${\displaystyle \frac{nRT}{V}{V}^{\beta }=\text{cte}\text{,}T{V}^{\beta -1}=\text{cte}}$

• La relación entre presión p y temperatura T es

${\displaystyle p{\left(\frac{nRT}{p}\right)}^{\beta }=\text{cte}\text{,}{p}^{1-\beta }{T}^{\beta }=\text{cte}}$

Representamos procesos politrópicos de índices: 0.2, 0.5, 3, 10, 100, -10, -2, -1, -0.5, 0

hold on
for n=[0.2,0.5,3,10,100, -10,-2,-1,-0.5,0]
    fplot(@(V) 1./V.^n,[0.25,2])
end
n=1.4;
fplot(@(V) 1./V.^n,[0.25,2],'color', 'r','lineWidth',1.2)
n=1;
fplot(@(V) 1./V.^n,[0.25,2],'color', 'b','lineWidth',1.2)
hold off
grid on
ylim([0,2.5])
xlabel('V')
ylabel ('p')
title('Procesos politrópicos')

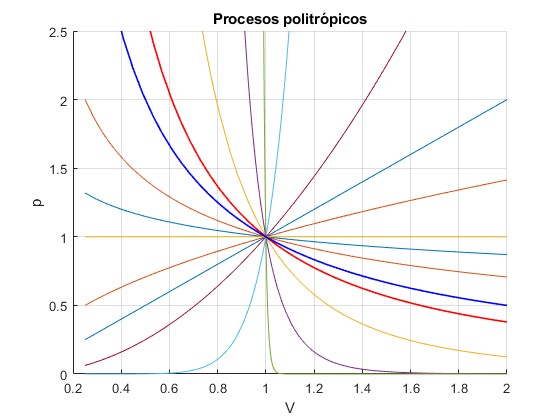
Los procesos con β>0 se representan en los cuadrantes 2° y 4°. Los procesos con β<0 se representan en los cuadrantes 1°y 3°. β=0 es un proceso a presión constante (línea horizontal), y β=100 es un proceso a volumen casi constante (línea vertical)

Las dos líneas más gruesas: la azul, es un proceso con β=1 (isotermo), la roja, es un proceso con β=1.4 (adiabático)

Trabajo

• El estado inicial está caracterizado por una presión p₁, un volumen V₁ y una temperatura T₁
• El estado final está caracterizado por una presión p₂, un volumen V₂ y una temperatura T₂

Se cumple que

${\displaystyle p{V}^{\beta }=p_1{V}_1^{\beta }=p_2{V}_2^{\beta }=\text{cte}}$

El trabajo vale

${\displaystyle \begin{array}{l}W={\displaystyle \underset{V_1}{\overset{V_2}{\int }}p·dV}={\displaystyle \underset{V_1}{\overset{V_2}{\int }}\frac{\text{cte}}{V^{\beta }}}dV=\frac{\text{cte}}{-\beta +1}\left(V_2^{-\beta +1}-V_1^{-\beta +1}\right)=\frac{1}{-\beta +1}\left(p_2{V}_2^{\beta }{V}_2^{-\beta +1}-p_1{V}_1^{\beta }{V}_1^{-\beta +1}\right)\\ W=\frac{p_2{V}_2-p_1{V}_1}{-\beta +1}\end{array}}$

Otra forma de expresar el trabajo

${\displaystyle W=\frac{p_1{V}_1^{\beta }}{-\beta +1}\left(V_2^{-\beta +1}-V_1^{-\beta +1}\right)=\frac{p_1{V}_1^{\beta }{V}_1^{-\beta +1}}{-\beta +1}\left({\left(\frac{V_2}{V_1}\right)}^{-\beta +1}-1\right)=\frac{p_1{V}_1}{-\beta +1}\left({\left(\frac{V_2}{V_1}\right)}^{-\beta +1}-1\right)}$

Teniendo en cuenta la relación entre los calores específicos a presión constante c_p y a volumen constante c_v

c_p=c_v+R, γ=c_p/c_v, c_v=R/(γ-1)

${\displaystyle \begin{array}{l}{T}_1{V}_1^{\beta -1}=T_2{V}_2^{\beta -1},\frac{T_1}{V_1^{-\beta +1}}=\frac{T_2}{V_2^{-\beta +1}},{\left(\frac{V_2}{V_1}\right)}^{-\beta +1}=\frac{T_2}{T_1}\\ W=\frac{nR{T}_1}{-\beta +1}\left(\frac{T_2}{T_1}-1\right)=\frac{n\left(c_p-c_v\right)}{-\beta +1}\left(T_2-T_1\right)=n{c}_v\frac{\gamma -1}{-\beta +1}\left(T_2-T_1\right)\end{array}}$

Variación de energía interna

La variación de energía interna entre los estados inicial y final es

${\displaystyle \Delta U=n{c}_v\left(T_2-T_1\right)}$

Calor

El primer principio de la Termodinámica, ΔU=Q-W, Q=ΔU+W

${\displaystyle \begin{array}{l}Q=n{c}_v\left(T_2-T_1\right)+n{c}_v\frac{\gamma -1}{-\beta +1}\left(T_2-T_1\right)=n{c}_v\frac{\beta -\gamma }{\beta -1}\left(T_2-T_1\right)=n{c}_{\beta }\left(T_2-T_1\right)\\ c_{\beta }=c_v\frac{\beta -\gamma }{\beta -1}=\frac{\beta c_v-c_p}{\beta -1}=\frac{R}{\gamma -1}\frac{\beta -\gamma }{\beta -1}\end{array}}$

Es la definición de calor específico c_β en un proceso politrópico

Representamos c_β/R en función de β, tomando el índice addibático γ=1.4

gamma=1.4;
f=@(x) (x-gamma)./((gamma-1)*(x-1));
hold on
fplot(f, [-1,3])
plot(0,7/2,'ro','markersize',3,'markerfacecolor','r')
line([-1,0],[7/2,7/2],'lineStyle','--')
line([0,0],[0,7/2],'lineStyle','--')
line([-1,3],[5/2,5/2],'lineStyle','--')
plot(gamma,0,'ro','markersize',3,'markerfacecolor','r')
hold off
grid on
ylim([-2,10])
xlabel('\beta')
ylabel ('c_\beta/R')
title('Calor específico c_\beta')

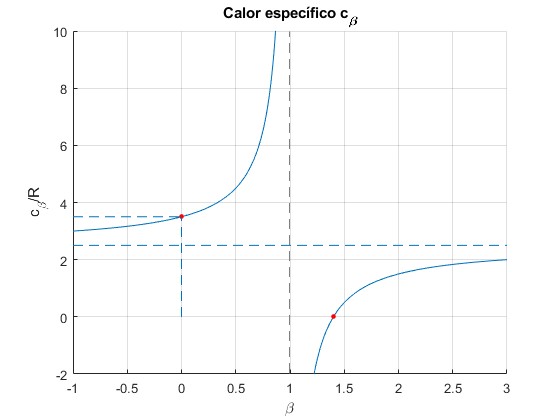
• Para un proceso a presión constante, β=0, c_β=c_p=7R/2
• Para un proceso adiabático, β=γ, c_β=0
• Para un proceso isotermo, β=1, c_β→∞
• Para un procso a volumen constante, β→∞, c_β→R/(γ-1)=c_v=5R/2. Esta es la ecuación de la asíntota horizontal

El calor específico c_β es negativo en el intervalo (1,γ)

Deducción alternativa de proceso politrópico

Hemos partido de la definición de proceso politrópico como pV^β=cte. Partimos ahora de, dQ=nc_βdT y llegamos a pV^β=cte, del siguiente modo

${\displaystyle \begin{array}{l}dU=dQ-pdV\\ n{c}_{v}dT=n{c}_{\beta }dT-pdV\\ n\left(c_{\beta }-c_v\right)dT=\frac{nRT}{V}dV\\ \frac{dT}{T}=\frac{R}{c_{\beta }-c_v}\frac{dV}{V}\\ \frac{dT}{T}-\frac{c_p-c_v}{c_{\beta }-c_v}\frac{dV}{V}=0\\ T{V}^{-\frac{c_p-c_v}{c_{\beta }-c_v}}=\text{cte}\\ p{V}^{1-\frac{c_p-c_v}{c_{\beta }-c_v}}=\text{cte}\\ p{V}^{\frac{c_{\beta }-c_p}{c_{\beta }-c_v}}=\text{cte}\\ \beta \text{=}\frac{c_{\beta }-c_p}{c_{\beta }-c_v},c_{\beta }=\frac{\beta c_v-c_p}{\beta -1}\end{array}}$

Relación entre trabajo y calor

Relacionamos el calor Q y el trabajo W

${\displaystyle \begin{array}{l}Q=n{c}_v\frac{\beta -\gamma }{\beta -1}\left(T_2-T_1\right)\\ W=n{c}_v\frac{\gamma -1}{-\beta +1}\left(T_2-T_1\right)\\ \frac{W}{Q}=\frac{\gamma -1}{\gamma -\beta }\end{array}}$

Representamos el cociente W/Q en función de β tomando γ=1.4 (aire)

gamma=1.4;
f=@(x) (gamma-1)./(gamma-x);
fplot(f, [-5,5])
line([1,1],[0,f(1)],'lineStyle','--')
line([-5,1],[f(1),f(1)],'lineStyle','--')
line([0,0],[0,f(0)],'lineStyle','--')
line([-5,0],[f(0),f(0)],'lineStyle','--')
grid on
ylim([-2.5,2.5])
xlabel('\beta')
ylabel ('W/Q')
title('Procesos politrópicos')

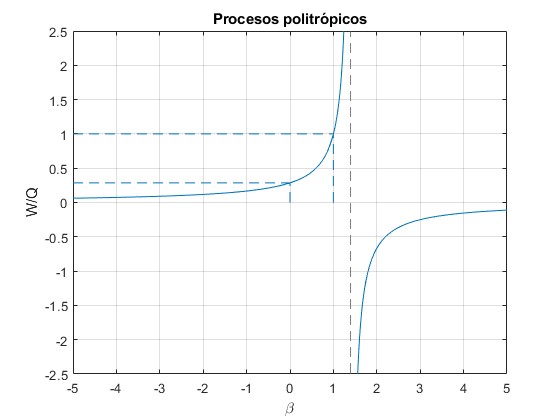
Para un proceso termodinámico caracterizado por un índice β<γ, el resultado es W/Q>0, parte del calor absorbido Q>0 se convierte en trabajo W>0 (el gas se expande). Si el gas se comprime W<0 el gas cede calor Q<0 a los alrededores del sistema.

• Adiabático

Cuando β=γ, el denominador se aproxima a cero, esto significa que el calor transferido desde o hacia el sistema tiende a cero.

• A presión constante

Para un proceso a presión constante, β=0 y γ=1.4 (para el aire) el cociente es W/Q=0.286, esto quiere decir, que el 28.6% del calor suministrado se convierte en trabajo, el resto se convierte en energía interna. Este resultado es independiente de la presión, volumen o temperatura del estado inicial y final de dicho proceso, solamente depende del tipo de gas.

• A temperatura constante

β=1, el cociente W/Q=1, el calor absorbido se convierte en trabajo, la variación de energía interna es cero, ΔU=0, la temperatura permanece constante

• A volumen constante

Para un proceso a volumen constante, β→∞, el denominador en la expresión W/Q tiende a -∞, el trabajo tiende a cero

Indice politrópico

Cuando se comprime el aire muy rápidamente, no hay tiempo de que el sistema transfiera calor a los alrededores, el aire incrementa su temperatura, el proceso es adiabático β=γ

Cuando se comprime aire muy lentamente, se transfiere calor a los alrededores, la temperatura del aire permanece constante, el proceso es isotermo, β=1

Un proceso real no será ni infinitamente rápido, ni infinitamente lento, el proceso politrópico tendrá un índice β comprendido entre 1 y γ.

Dados el estado inicial y final, el índice del proceso politrópico se calcula despejando β.

• Conocida la presión y el volumen

${\displaystyle \begin{array}{l}{p}_1{V}_1^{\beta }=p_2{V}_2^{\beta },\frac{p_1}{p_2}={\left(\frac{V_2}{V_1}\right)}^{\beta }\\ \beta =\frac{\ln \left(\frac{p_1}{p_2}\right)}{\ln \left(\frac{V_2}{V_1}\right)}\end{array}}$

• Conocida la temperatura y el volumen

${\displaystyle \begin{array}{l}{T}_1{V}_1^{\beta -1}=T_2{V}_2^{\beta -1},\frac{T_1}{T_2}={\left(\frac{V_2}{V_1}\right)}^{\beta -1}\\ \beta =1+\frac{\ln \left(\frac{T_1}{T_2}\right)}{\ln \left(\frac{V_2}{V_1}\right)}\end{array}}$

• Conocida la temperatura y la presión

${\displaystyle \begin{array}{l}{p}_1^{1-\beta }{T}_1^{\beta }=p_2^{1-\beta }{T}_2^{\beta },{\left(\frac{p_1}{p_2}\right)}^{1-\beta }={\left(\frac{T_2}{T_1}\right)}^{\beta }\\ \left(1-\beta \right)\ln \left(\frac{p_1}{p_2}\right)=\beta \ln \left(\frac{T_2}{T_1}\right)\\ \beta =\frac{\ln \left(\frac{p_1}{p_2}\right)}{\ln \left(\frac{p_1}{p_2}\right)+\ln \left(\frac{T_2}{T_1}\right)}\end{array}}$

Cuando 1<β<γ el calor específico c_β<0. La idea de calor específico negativo parace algo extraña, ya que la tempartaura del gas ΔT>0 se incrementa a la vez que el gas cede calor Q<0 o viceversa

Procesos isotermo, adiabático y politrópico

Estado inicial del gas

p₁=17.5 atm, V₁=0.2124 l, T₁=2000 K

Estado final

V₁=1 l

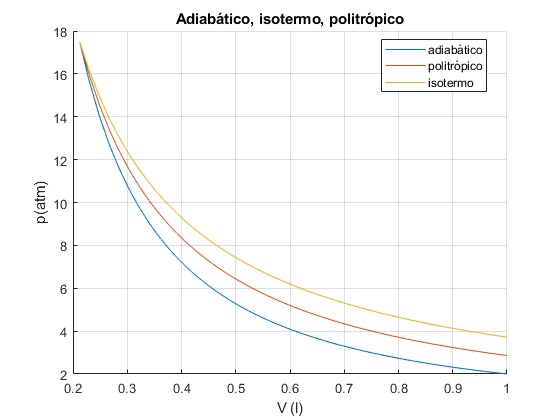
Representamos los tres procesos: isotermo, adiabático y politrópico entre el estado incial y el estado final. Calculamos la presión p₂ y la temperatura T₂ del estado final

Calculamos el calor Q, trabajo W y variación de energía interna, ΔU en cada uno de los procesos

gamma=1.4;
beta=1.1689;
p1=17.5; %estado inicial
V1=0.2124;
T1=2000;
V2=1; %estado final
hold on
fplot(@(x) p1*V1^gamma./x.^gamma, [V1,V2])
fplot(@(x) p1*V1^beta./x.^beta, [V1,V2])
fplot(@(x) p1*V1./x, [V1,V2])
hold off
grid on
xlabel('V (l)')
legend('adiabático','politrópico','isotermo','location','best')
ylabel ('p(atm)')
title('Adiabático, isotermo, politrópico')

%isotermo
p2=p1*V1/V2;
T2=2000;
Du=0;
W=p1*V1*log(V2/V1);
Q=W;
fprintf('isotermo: p2=%1.3f, T2=%4.1f, Du=%1.3f, Q=%1.3f, W=%1.3f\n',
 p2, T2, Du, Q, W)
%adiabático
p2=p1*V1^gamma/V2^gamma;
T2=T1*V1^(gamma-1)/V2^(gamma-1);
Du=5*p1*V1*(T2-T1)/(2*T1);
Q=0;
W=(p2*V2-p1*V1)/(-gamma+1);
fprintf('adiabático: p2=%1.3f, T2=%4.1f, Du=%1.3f, Q=%1.3f, W=%1.3f\n', 
p2, T2, Du, Q, W)
%politrópico
p2=p1*V1^beta/V2^beta;
T2=T1*V1^(beta-1)/V2^(beta-1);
Du=5*p1*V1*(T2-T1)/(2*T1);
Q=p1*V1*(beta-gamma)*(T2-T1)/(T1*(gamma-1)*(beta-1));
W=(p2*V2-p1*V1)/(-beta+1);
fprintf('politrópico: p2=%1.3f, T2=%4.1f, Du=%1.3f, Q=%1.3f, W=%1.3f\n', 
p2, T2, Du, Q, W)

isotermo: p2=3.717, T2=2000.0, Du=0.000, Q=5.759, W=5.759
adiabático: p2=2.000, T2=1076.2, Du=-4.292, Q=0.000, W=4.292
politrópico: p2=2.861, T2=1539.5, Du=-2.139, Q=2.927, W=5.067

• Proceso isotermo

${\displaystyle p_1{V}_1=p_2{V}_2}$

El trabajo y el calor

El resultado es p₂=3.717 atm, la temperatura T₂=2000 K

${\displaystyle \begin{array}{l}\Delta U=0\\ W=nRT\ln \frac{V_2}{V_1}=p_1{V}_1\ln \frac{V_2}{V_1}=5.759\text{J}\\ Q=W\end{array}}$

• Proceso adiabático, γ=1.4 (para el aire)

${\displaystyle \begin{array}{l}{p}_1{V}_1^{\gamma }=p_2{V}_2^{\gamma }\\ T_1{V}_1^{\gamma -1}=T_2{V}_2^{\gamma -1}\end{array}}$

El resultado es p₂=2.0 atm, la temperatura T₂=1076.2 K

El trabajo y la varición de energía interna

${\displaystyle \begin{array}{l}\Delta U=n{c}_v\left(T_2-T_1\right)=\frac{5}{2}nR\left(T_2-T_1\right)=\frac{5}{2}\frac{p_1{V}_1}{T_1}\left(T_2-T_1\right)=\text{ 4}\text{.292}\text{J}\\ Q=0\\ W=\frac{p_2{V}_2-p_1{V}_1}{-\gamma +1}=\text{4}\text{.292}\text{J}\end{array}}$

Se cumple el primer principio de la Termodinámica, ΔU=Q-W

• Proceso politrópico, β=1.1689

${\displaystyle \begin{array}{l}{p}_1{V}_1^{\beta }=p_2{V}_2^{\beta }\\ T_1{V}_1^{\beta -1}=T_2{V}_2^{\beta -1}\end{array}}$

El resultado es p₂=2.861 atm, la temperatura T₂=1539.5 K

El trabajo, calor y la variación de energía interna

${\displaystyle \begin{array}{l}\Delta U=n{c}_v\left(T_2-T_1\right)=\frac{5}{2}nR\left(T_2-T_1\right)=\frac{5}{2}\frac{p_1{V}_1}{T_1}\left(T_2-T_1\right)=\text{ -2}\text{.139}\text{J}\\ Q=n{c}_{\beta }\left(T_2-T_1\right)=\frac{nR}{\gamma -1}\frac{\beta -\gamma }{\beta -1}\left(T_2-T_1\right)=\frac{p_1{V}_1}{T_1}\frac{1}{\gamma -1}\frac{\beta -\gamma }{\beta -1}\left(T_2-T_1\right)=\text{ 2}\text{.927}\text{J}\\ W=\frac{p_2{V}_2-p_1{V}_1}{-\beta +1}=\text{ 5}\text{.067}\text{J}\end{array}}$

Se cumple el primer principio de la Termodinámica, ΔU=Q-W

Expansión rápida de una mezcla de aire con vapor saturado

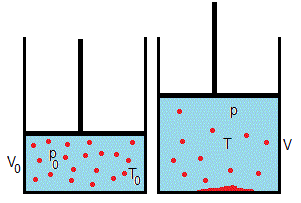
Un recipiente de volumen V₀ contiene aire y vapor saturado a la temperatura T₀. El émbolo ejerce una presión p₀.

El número de moles de vapor saturado es

${\displaystyle n_{v0}=\frac{P_{v0}{V}_0}{R{T}_0}}$

Donde M_H2O=18 g/mol es la masa molecular del agua y R=8.3143 J/(K·mol) es la constante de los gases.

Supondremos que el vapor se comporta como un gas ideal cuya presión parcial P_v0 se puede consultar en las tablas o deducir de fórmulas empíricas de ajuste de los datos experimentales. Por ejemplo, para T₀=19 °C (292 K) la presión de vapor saturado es P_v0=2 198 Pa

Cuando el émbolo se desplaza rápidamente. El volumen de aire aumenta a V y la temperatura disminuye de T₀ a T=T₀-ΔT, con ΔT<<T₀

Al disminuir la temperatura de la mezcla, la presión de vapor P_v se reduce, una parte del vapor inicial n_v se condensa.

${\displaystyle n_v=\frac{P_{v}V}{RT}}$

El número de moles de vapor que se ha condensado es la diferencia

${\displaystyle n=\frac{P_{v0}{V}_0}{R{T}_0}-\frac{P_{v}V}{RT}}$

El calor generado en la condensación será

${\displaystyle Q=nL=\frac{L}{R}\left(\frac{P_{v0}{V}_0}{T_0}-\frac{P_{v}V}{T}\right)}$

Donde L=43 509 J/mol es el valor de la entalpía de vaporización

Como el proceso de expansión es rápido, la mezcla aire-vapor no tiene tiempo de intercambiar calor con el medio ambiente a través de las paredes del recipiente

La presión de vapor viene dada por la fórmula de Clausius-Clapeyron

${\displaystyle P_v=P_{v_0}\exp \left(\frac{L}{R}\left(\frac{1}{T_0}-\frac{1}{T}\right)\right)}$

Sustituimos la presión parcial de vapor P_v en la expresión del calor generado en la condensación

${\displaystyle Q=\frac{L}{R}{P}_{v0}\left(\frac{V_0}{T_0}-\exp \left(\frac{L}{R}\left(\frac{1}{T_0}-\frac{1}{T}\right)\right)\frac{V}{T}\right)}$

Proceso politrópico

Entre el estado inicial y final se produce un proceso politrópico de índice β que vamos a determinar

${\displaystyle \begin{array}{l}p{V}^{\beta }=p_0{V}_0^{\beta }\\ p{\left(\frac{nRT}{p}\right)}^{\beta }=p_0{\left(\frac{nR{T}_0}{p_0}\right)}^{\beta }\\ p^{1-\beta }{T}^{\beta }=p_0^{1-\beta }{T}_0^{\beta }\\ \frac{p}{p_0}={\left(\frac{T_0}{T}\right)}^{\beta /(1-\beta )}\\ \frac{V}{T}=\frac{nR}{p}=\frac{nR}{p_0}{\left(\frac{T_0}{T}\right)}^{\beta /(\beta -1)}\end{array}}$

El número n de moles de la mezcla (aire+vapor) no permence constante ya que una parte del vapor inicial se condensa. Si esta parte es pequeña, en comparación con el número total de moles, se podría considerar que n es casi constante.

En un proceso politrópico, el calor Q es

${\displaystyle \begin{array}{l}Q=n{c}_{\beta }\left(T-T_0\right)=-n{c}_{\beta }\Delta T\\ c_{\beta }=\frac{R}{\gamma -1}\frac{\beta -\gamma }{\beta -1}\end{array}}$

Determinación del índice β

Introduciendo V/T, la expresión del calor generado en la condensación es

${\displaystyle \begin{array}{l}Q=\frac{L}{R}{P}_{v0}\left(\frac{nR}{p_0}-\exp \left(\frac{L}{R}\left(\frac{1}{T_0}-\frac{1}{T}\right)\right)\frac{nR}{p_0}{\left(\frac{T_0}{T}\right)}^{\beta /(\beta -1)}\right)\\ Q=n\frac{P_{v0}}{p_0}L\left(1-\exp \left(\frac{L}{R}\left(\frac{1}{T_0}-\frac{1}{T}\right)\right){\left(\frac{T_0}{T}\right)}^{\beta /(\beta -1)}\right)\\ Q=n\frac{P_{v0}}{p_0}L\left(1-\exp \left(\frac{L}{R{T}_0}\left(1-\frac{T_0}{T_0-\Delta T}\right)\right){\left(\frac{T_0}{T_0-\Delta T}\right)}^{\beta /(\beta -1)}\right)\\ Q=n\frac{P_{v0}}{p_0}L\left(1-\exp \left(-\frac{L}{R{T}_0}\left(\frac{x}{1-x}\right)\right){\left(1-x\right)}^{-\beta /(\beta -1)}\right),x=\frac{\Delta T}{T_0}\end{array}}$

Dado que las temperaturas inicial y final son próximas, T=T₀-ΔT, con ΔT<<T₀, desarrollamos en serie tomando el término en ΔT

Utilizamos la función taylor de MATLAB, se omite la constante delante del paréntesis, las variables x es ΔT/T₀, b es β y a es L/(RT₀)

>> syms x b a;
>> y=1-exp(-a*x/(1-x))*(1-x)^(-b/(b-1));
>> taylor(y,x,0,'order',2)
ans =x*(a - b/(b - 1))

${\displaystyle Q\approx n\left\{\frac{P_{v0}}{p_0}\frac{L}{T_0}\left(\frac{L}{R{T}_0}-\frac{\beta }{\beta -1}\right)\right\}\Delta T}$

Comparamos con el calor del proceso politrópico

${\displaystyle Q=-n\left\{\frac{R}{\gamma -1}\frac{\beta -\gamma }{\beta -1}\right\}\Delta T}$

Despejamos el índice β

${\displaystyle \begin{array}{l}\frac{P_{v0}}{p_0}\frac{L}{T_0}\left(\frac{L}{R{T}_0}-\frac{\beta }{\beta -1}\right)=-\frac{R}{\gamma -1}\frac{\beta -\gamma }{\beta -1}\\ \beta =\frac{{\left(\frac{L}{R{T}_0}\right)}^2\frac{P_{v0}}{p_0}\left(\gamma -1\right)+\gamma }{\left(\frac{L}{R{T}_0}\right)\frac{P_{v0}}{p_0}\left(\gamma -1\right)\left(\frac{L}{R{T}_0}-1\right)+1}\end{array}}$

Si no hay vapor o la presión es muy pequeña, P_v0≈0, entonces β=γ el proceso es adiabático

Creamos un script para calcular el índice β dada la presión inicial p₀ en atmósferas. Datos

• Presión atmosférica, 1.013·10⁵ N/m²
• Temperatura ambiente, T₀=19 °C=292 K
• Presión de vapor a esta temperatura, P_v0=2 198 Pa
• Indice adiabático de un gas ideal, γ=1.4
• Constante de los gases, R=8.3143 J/(K·mol)
• Calor de vaporización, L=43 509 J/mol

gamma=1.4; %índice adiabático
L=43509; %calor de vaporización J/mol
T0=292; %temperatura inicial
Pv=2.1983e3;%presión de vapor
R=8.3143; %constante de los gases 
for p=[4.8,4.4,4.0,3.6,3.2] %presión en atmósferas
    P0=p*1.013e5;
    beta=(Pv*L^2*(gamma-1)/(R^2*T0^2*P0)+gamma)/(1+Pv*L*(gamma-1)*
(L/(R*T0)-1)/(R*P0*T0));
    disp([p,beta])
end

    4.8000    1.2793
    4.4000    1.2724
    4.0000    1.2647
    3.6000    1.2560
    3.2000    1.2461

Son similares a la tercera columna de la tabla I del artículo de Romanelli, pág. 764

Fórmula barométrica

En la página titulada 'Modelos simples de atmósfera', calculamos la variación de la presión del aire en función de la altura por encima del nivel del mar. Suponíamos que la atmósfera está en equilibrio y que su temperatura se mantenía constante, pV=cte.

En este caso, la relación entre presión y volumen responde al la fórmula pV^β=cte

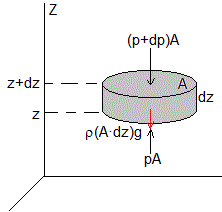
Las fuerzas que actúan sobre el elemento de fluido (aire) de densidad ρ, un cilindro de base A y altura dz

• La que ejerce la presión sobre la cara superior, (p+dp)A
• La que ejerce la presión sobre la cara inferior, (p+dp)A
• El peso, ρ(A·dz)g

Las fuerzas que ejerce la presión sobre la superficie lateral se anulan

En el equilibrio

${\displaystyle \begin{array}{l}(p+dp)A+\rho (A·dz)g=pA\\ dp=-\rho g·dz\end{array}}$

Supongamos ahora que la relación entre presión y volumen es de la forma

${\displaystyle \begin{array}{l}p{V}^{\beta }=p_0{V}_0^{\beta }\\ p{\rho }^{-\beta }=p_0{\rho }_0^{-\beta }\\ \rho ={\rho }_0{\left(\frac{p}{p_0}\right)}^{1/\beta }\end{array}}$

Donde p₀ y ρ₀ son la presión y densidad a la altura z=0

Integramos la ecuación diferencial

${\displaystyle \begin{array}{l}p=-{\rho }_0{\left(\frac{p}{p_0}\right)}^{1/\beta }g·dz\\ {\displaystyle \underset{p_0}{\overset{p}{\int }}\frac{dp}{p^{1/\beta }}}=-{\rho }_0{p}_0^{-1/\beta }g{\displaystyle \underset{0}{\overset{z}{\int }}dz}\\ \frac{1}{-\frac{1}{\beta }+1}\left(p^{-1/\beta +1}-p_0^{-1/\beta +1}\right)=-{\rho }_0{p}_0^{-1/\beta }gz\\ z=\frac{\beta }{\beta -1}\frac{1}{{\rho }_{0}g}\left(p_0-p^{\frac{\beta -1}{\beta }}{p}_0^{1/\beta }\right)=\frac{\beta }{\beta -1}\frac{p_0}{{\rho }_{0}g}\left(1-{\left(\frac{p}{p_0}\right)}^{\frac{\beta -1}{\beta }}\right)\end{array}}$

Utilizando la ecuación de estado del un gas ideal

${\displaystyle \begin{array}{l}pV=\frac{m}{M}RT\\ p=\frac{\rho }{M}RT\end{array}}$

El resultado es

${\displaystyle z=\frac{\beta }{\beta -1}\frac{\frac{{\rho }_0}{M}R{T}_0}{{\rho }_{0}g}\left(1-{\left(\frac{p}{p_0}\right)}^{\frac{\beta -1}{\beta }}\right)=\frac{\beta }{\beta -1}\frac{R{T}_0}{Mg}\left(1-{\left(\frac{p}{p_0}\right)}^{\frac{\beta -1}{\beta }}\right)}$

Despejamos la presión

${\displaystyle p=p_0{\left(1-\frac{\beta -1}{\beta }\frac{Mgz}{R{T}_0}\right)}^{\frac{\beta }{\beta -1}}}$

Llamamos

${\displaystyle \begin{array}{l}x=-\frac{\beta -1}{\beta }\frac{Mgz}{R{T}_0}\\ p=p_0{\left\{{\left(1+x\right)}^{\frac{1}{x}}\right\}}^{-\frac{Mgz}{R{T}_0}}\end{array}}$

Cuando β→1 (proceso isotermo), x→0, (1+x)^1/x→e (número e)

>> syms x;
>> limit((1+x)^(1/x),x,0)
ans =exp(1)

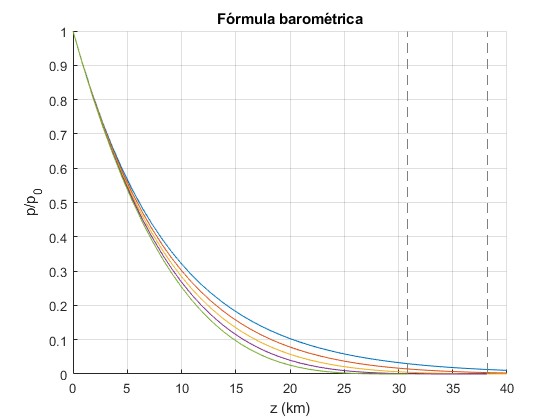
La variación de presión p con la altura z que obtuvimos para una atmósfera isoterma

${\displaystyle p=p_0\exp \left(-\frac{Mgz}{R{T}_0}\right)}$

Datos

• Masa molecular del aire, M=28.9 g/mol
• Constante de los gases, R=8.3143 J/(K·mol)
• Temperatura para z=0, T₀=300 k

R=8.3143; %constante de los gases
T0=300; %temperatura a nivel del mar
M=28.9/1000; %masa molecular del aire en kg/mol
hold on
f=@(z) exp(-M*9.8*1000*z/(R*T0)); %n=1
fplot(f,[0,40])
for n=1.1:0.1:1.4
    f=@(z) (1-(n-1)*M*9.8*z*1000/(n*R*T0)).^(n/(n-1));
    fplot(f,[0,40])
end
grid on
xlabel('z (km)')
ylabel('p/p_0')
title('Fórmula barométrica')

Referencias

Polytropic process in a closed system. tec-science (07/11/2021)

Alejandro Romanelli, Italo Bove, Federico González Madina. Air expansion in a water rocket. Am. J. Phys. 81 (10), October 2013, pp. 762-766

W EI Guo-zhu，GU Yong-wei，DU An. The improvement on the barometric formula in isothermal process of the gas. College Physics, Volume 25, Issue 11, 20 November 2006