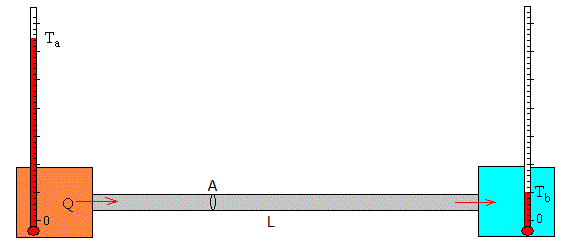
Consideremos una varilla de longitud L y sección A perfectamente aislada, hecha de una material de conductividad térmica K. Los extremos están conectados a un foco caliente a la temperatura constante T_a y a un foco frío a la temperatura T_b

Estado transitorio

En una varilla metálica, el calor fluye desde las regiones donde la temperatura es más alta hacia las regiones en la que es más baja. La ley de Fourier establece que el flujo de calor J (energía por unidad de área y unidad de tiempo es proporcional al gradiente de temperatura.

${\displaystyle J=-K\frac{\partial T}{\partial x}}$

donde K se denomina conductividad térmica del material

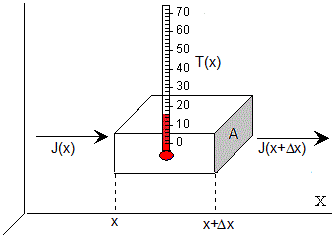
Sea una varilla de longitud L y área de la sección transversal A, con una distribución de temperatura no uniforme a lo largo del eje X, desde x=0 hasta x=L. La varilla está hecha de un material de densidad ρ, calor específico c y conductividad térmica K.

Vamos a considerar un trozo de varilla de longitud Δx, entre x y x+Δx. En un intervalo de tiempo Δt, entra calor por su sección izquierda J(x)A·Δt y sale calor por su sección derecha J(x+Δx)A·Δt. La variación de entropía en este elemento diferencial de la varilla es

${\displaystyle \Delta S=\frac{J(x)A·\Delta t-J(x+\Delta x)A·\Delta t}{T(x)}=\frac{1}{T(x)}\left(-\frac{\partial J}{\partial x}dx\right)A\Delta t=\frac{1}{T(x)}\left(K\frac{{\partial }^{2}T}{\partial x^2}dx\right)A\Delta t}$

• La variación de entropía de la varilla en el intervalo de tiempo entre t y t+Δt es

${\displaystyle \Delta S=\left(KA{\displaystyle \underset{0}{\overset{L}{\int }}\frac{1}{T(x)}\frac{{\partial }^{2}T}{\partial x^2}dx}\right)\Delta t}$

La producción de entropía de la varilla, (dS/dt)_b es

${\displaystyle $ {\left(\frac{dS}{dt}\right)}_b=KA{\displaystyle \underset{0}{\overset{L}{\int }}\frac{1}{T(x)}\frac{{\partial }^{2}T}{\partial x^2}dx}$}$

• La variación de entropía de los focos en el intervalo de tiempo entre t y t+Δt



${\displaystyle \Delta S=-\frac{J(0)A·\Delta t}{T_a}+\frac{J(L)A·\Delta t}{T_b}=KA\left\{\frac{1}{T_a}{\left(\frac{\partial T}{\partial x}\right)}_{x=0}-\frac{1}{T_b}{\left(\frac{\partial T}{\partial x}\right)}_{x=L}\right\}\Delta t}$

La producción de entropía de los focos, (dS/dt)_f es

${\displaystyle {\left(\frac{dS}{dt}\right)}_f=KA\left\{\frac{1}{T_a}{\left(\frac{\partial T}{\partial x}\right)}_{x=0}-\frac{1}{T_b}{\left(\frac{\partial T}{\partial x}\right)}_{x=L}\right\}}$

Evolución de las temperaturas en cada punto de la varilla

La temperatura en cualquier punto de la varilla x, en un instante t, se compone de la suma de un término proporcional a x y de una serie rápidamente convergente que describe el estado transitorio.

${\displaystyle \begin{array}{l}T(x,t)=T_a+(T_b-T_a)\frac{x}{L}+{\displaystyle \sum _{n=1}^{\infty }{A}_n\sin \left(n\pi \frac{x}{L}\right)\exp \left(-\alpha \frac{n^2{\pi }^2}{L^2}t\right)}\\ A_n=\{\begin{array}{l}\frac{2}{n\pi }(2T_0-T_a-T_b)n \text{impar}\\ \frac{2}{n\pi }(T_b-T_a)n \text{par}\end{array}\end{array}}$

Sea una varilla hecha de cobre de

• Longitud, L= 50 cm
• Sección, A=1 cm²
• Densidad, ρ=8900 kg/m³
• Calor específico, c=390 J/(kg·K)
• Conductividad térmica, K=389.6 W/(m·K)
• Temperartura del foco caliente, T_a=373 K
• Temperartura del foco frío, T_b=293 K
• Temperartura inicial de la varillla, T₀=293 K

Definimos una función que calcula, la temperatura de un punto x de la varilla en el instante t

function T=temperatura(t, x)
   if(t==0)
       T=T0;
       return;
   end
   k=zeros(2,1);  
   k(1)=2*(2*T0-(Ta+Tb))/pi;
   k(2)=2*(Tb-Ta)/pi;
   cte=pi^2/(alfa*L^2);
   
   T=Ta+(Tb-Ta)*x/L;
   n=0;
   v=1;
   while(v>0.01)
        for j=1:2
            n=n+1;
            v=exp(-cte*n^2*t);
            T=T+v*k(j)*sin(pi*n*x/L)/n;
        end
   end
end

Una serie infinita tenemos que interrumpirla en algún término de acuerdo con algún criterio. Un posible criterio sería que la exponencial

${\displaystyle \exp \left(-\alpha \frac{n^2{\pi }^2}{L^2}t\right)<0.01}$

sea menor que un valor prefijado, por ejemplo 0.01.

Representamos la evolución de la temperatura en los puntos x de la varilla en varios instantes t

function varilla
    Ta=373; %temperatura en el extremo izquierdo
    Tb=293; %temperatura en el extremo derecho
    T0=293; %temperatura inicial de la varilla
    rho=8900; %densidad
    c=390; %calor específico
    K=389.6; %conductividad térmica
    alfa=rho*c/K; %Coeficiente, 1/alfa del aluminio
    L=0.5; % longitud de la varilla

    hold on
    xx=linspace(0,L,100);
    T=zeros(1,length(xx));
    axis([0 0.5 18 100]);
    for t=[10 100 500,1000]
        i=1;
        for x=xx
            T(i)=temperatura(t,x);
            i=i+1;
        end
        plot(xx,T-273,'displayName',num2str(t));
    end
    title('Evolución de la temperatura de una varilla')
    xlabel('x')
    ylabel('T')
    legend('-DynamicLegend','location','northeast')
    grid on
    hold off 

    function T=temperatura(t, x)
        if(t==0)
            T=T0;
            return;
        end
        k=zeros(2,1);  
        k(1)=2*(2*T0-(Ta+Tb))/pi;
        k(2)=2*(Tb-Ta)/pi;
        cte=pi^2/(alfa*L^2);
   
        T=Ta+(Tb-Ta)*x/L;
        n=0;
        v=1;
        while(v>0.01)
            for j=1:2
                n=n+1;
                v=exp(-cte*n^2*t);
                T=T+v*k(j)*sin(pi*n*x/L)/n;
            end
        end
    end

end

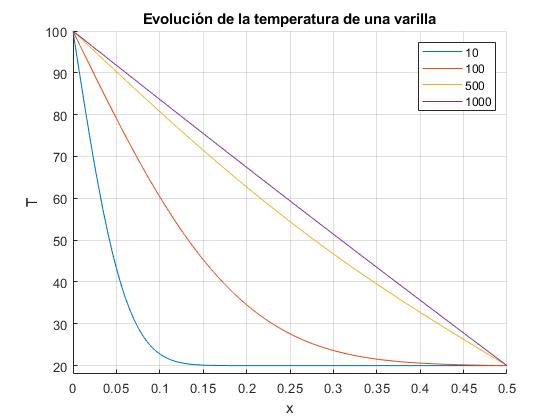
Observamos que el estado estacionario se va estableciendo, aproximadamante a partir de t=500 s

Calculamos la derivada primera y segunda respecto de x de la función T(x,t)

${\displaystyle \begin{array}{l}\frac{\partial T}{\partial x}=(T_b-T_a)\frac{1}{L}+\frac{1}{L}{\displaystyle \sum _{n=1}^{\infty }{A}_n\left(n\pi \right)\cos \left(n\pi \frac{x}{L}\right)\exp \left(-\alpha \frac{n^2{\pi }^2}{L^2}t\right)}\\ \frac{{\partial }^{2}T}{\partial x^2}=-\frac{1}{L^2}{\displaystyle \sum _{n=1}^{\infty }{A}_n{\left(n\pi \right)}^2\sin \left(n\pi \frac{x}{L}\right)\exp \left(-\alpha \frac{n^2{\pi }^2}{L^2}t\right)}\end{array}}$

Definimos dos funciones, una que calcula la derivada primera y otra la segunda de la función T(x,t) respecto de x

function T=primera(t, x)
   k=zeros(2,1);  
   k(1)=2*(2*T0-(Ta+Tb));
   k(2)=2*(Tb-Ta);
   cte=pi^2/(alfa*L^2);
   
   T=(Tb-Ta)/L;
   n=0;
   v=1;
   while(v>0.01)
        for j=1:2
            n=n+1;
            v=exp(-cte*n^2*t);
            T=T+v*k(j)*cos(pi*n*x/L)/L;
        end
   end
end

function T=segunda(t, x)
   k=zeros(2,1);  
   k(1)=2*(2*T0-(Ta+Tb))*pi;
   k(2)=2*(Tb-Ta)*pi;
   cte=pi^2/(alfa*L^2);
   
   T=0;
   n=0;
   v=1;
   while(v>0.01)
        for j=1:2
            n=n+1;
            v=exp(-cte*n^2*t);
            T=T-v*k(j)*sin(pi*n*x/L)*n/L^2;
        end
   end
end

Estado estacionario

El estado estacionario está caracterizado, por temperaturas fijas a lo largo de la varilla que van disminuyendo linealmente

${\displaystyle T(x,\infty )=T_a+\frac{T_b-T_a}{L}x}$

El flujo de calor J_∞=K(T_a-T_b)/L es constante. Los elementos diferenciales de la varilla no acumulan calor, por lo que no contribuyen a la producción de entropía (dS/dt)_b=0

En la unidad de tiempo, se transfiere a través de la varilla una cantidad de calor JA del foco caliente al foco frío. Como el foco frío absorbe calor, su entropía aumenta, JA/T_b. Al mismo tiempo, como el foco caliente pierde calor su variación de entropía es -JA/T_a

Como T_a>T_b, la variación de entropía del sistema formado por la varilla y los dos focos es positivo

${\displaystyle {\left(\frac{dS}{dt}\right)}_{t\to \infty }=\frac{JA}{T_b}-\frac{JA}{T_a}=\frac{KA}{L}\frac{{\left(T_a-T_b\right)}^2}{T_a{T}_b}}$

Cálculo de la producción dS/dt de entropía

Representamos la produción de entropía

• de la varilla, (dS/dt)_b
• de los focos, (dS/dt)_f
• la suma de ambos términos

en función del tiempo t.

function varilla_1
    Ta=373; %temperatura en el extremo izquierdo
    Tb=293; %temperatura en el extremo derecho
    T0=293; %temperatura inicial de la varilla
    rho=8900; %densidad
    c=390; %calor específico
    K=389.6; %conductividad térmica
    alfa=rho*c/K; %Coeficiente, 1/alfa del aluminio
    L=0.5; % longitud de la varilla
    A=1e-4; %sección, 1 cm^2

    tt=20:5:1000;
    entropia_varilla=zeros(1,length(tt));
    entropia_focos=zeros(1,length(tt));
    i=1;
    for t=tt
        f=@(x) segunda(t,x)./temperatura(t,x);
        entropia_varilla(i)=K*A*integral(f,0,L);
        entropia_focos(i)=K*A*(primera(t,0)/Ta-primera(t,L)/Tb);
        i=i+1;
    end
    plot(tt,entropia_varilla, 'r', tt, entropia_focos, 'b',tt, 
(entropia_varilla+entropia_focos),'k');
    entropia_fin=K*A*(Ta-Tb)^2/(L*Ta*Tb); %estado estacionario
    line([0,t],[entropia_fin, entropia_fin],'color','k','lineStyle','--')
    title('Evolución de la entropía')
    legend('varilla','focos','total','Location','best')
    ylim([-0.05,0.05])
    xlabel('t')
    ylabel('dS/dt')
    grid on

    function T=temperatura(t, x)
        if(t==0)
            T=T0;
            return;
        end
        k=zeros(2,1);  
        k(1)=2*(2*T0-(Ta+Tb))/pi;
        k(2)=2*(Tb-Ta)/pi;
        cte=pi^2/(alfa*L^2);
   
        T=Ta+(Tb-Ta)*x/L;
        n=0;
        v=1;
        while(v>0.01)
            for j=1:2
                n=n+1;
                v=exp(-cte*n^2*t);
                T=T+v*k(j)*sin(pi*n*x/L)/n;
            end
        end
    end

    function T=primera(t, x) %derivada primera
        k=zeros(2,1);  
        k(1)=2*(2*T0-(Ta+Tb));
        k(2)=2*(Tb-Ta);
        cte=pi^2/(alfa*L^2);
   
        T=(Tb-Ta)/L;
        n=0;
        v=1;
        while(v>0.01)
            for j=1:2
                n=n+1;
                v=exp(-cte*n^2*t);
                T=T+v*k(j)*cos(pi*n*x/L)/L;
            end
        end
    end

    function T=segunda(t, x) %derivada segunda
        k=zeros(2,1);  
        k(1)=2*(2*T0-(Ta+Tb))*pi;
        k(2)=2*(Tb-Ta)*pi;
        cte=pi^2/(alfa*L^2);
   
        T=0;
        n=0;
        v=1;
        while(v>0.01)
            for j=1:2
                n=n+1;
                v=exp(-cte*n^2*t);
                T=T-v*k(j)*sin(pi*n*x/L)*n/L^2;
            end
        end
    end
end

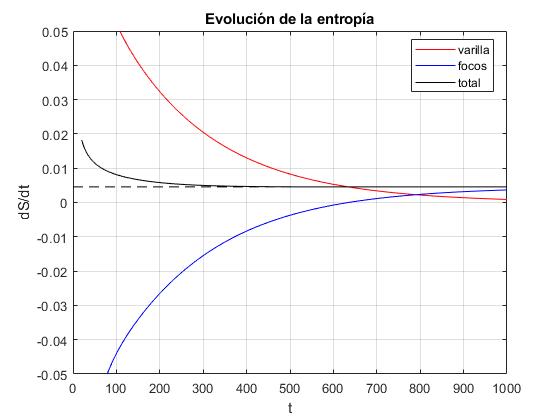
En la figura, observamos que la producción de entropía en la varilla tiende a cero (curva de color rojo), la producción de entropía de los focos tiende hacia el valor en el estado estacionario (azul). La producción de entropía es la suma de ambas contribuciones dS/dt>0 (negro). La línea horizontal a trazos de color negro, nos proporciona el valor de la producción de entropía en el estado estacionario (dS/dt)_∞

La producción de entropía en los focos (dS/dt)_f al principio es negativa, ya que el foco caliente cede calor para calentar la varilla y llega muy poco al foco frío. Se puede comprobar en el código J(0) es al principio muy grande y J(L) es pequeño

Para calcular la variación de entropía entre dos instantes, basta hacer la integral

${\displaystyle \Delta S={\displaystyle \underset{t_0}{\overset{t}{\int }}\left(\frac{dS}{dt}\right)}dt}$

Utilizamos la función trapz de MATLAB para efectuar esta integral entre los instantes 20 y 1000 s. Insertamos las líneas de código

...
    entropia=trapz(tt, entropia_varilla+entropia_focos);
    disp(entropia)
...

 5.3239

Referencias

Enrique N. Miranda. Entropy production in a heat conduction problem. Revista Brasileira de Ensino de Física, vol. 38, nº 4, e4303 (2016). https://www.scielo.br/j/rbef/i/2016.v38n4/