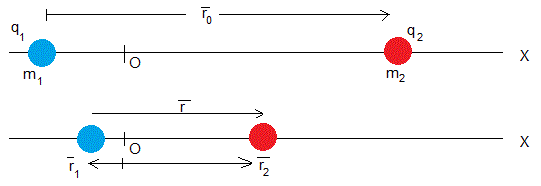
Consideremos el caso de un sistema aislado de dos partículas de masas m₁ y m₂ que además están cargadas con cargas q₁ y q₂ ,respectivamente

En la figura, se muestra su situación inicial en reposo, el origen O se establece en su centro de masas. La partícula de masa m₁ y carga q₁ a la izquierda del origen en la posición r₀₁ y la partícula de masa m₂ y carga q₂ a la derecha del origen en la posición r₀₂, de modo que se cumple que m₁·r₀₁+m₂·r₀₂=0

Se sueltan las partículas y pueden ocurrir los siguientes casos, según sea el signo de las cargas:

1. Las cargas de las partículas son del mismo signo. Las fuerzas de interacción gravitatoria y eléctrica son de signos contrarios

• La fuerza de repulsión entre cargas supera a la fuerza de atracción, las partículas se alejan, r>r₀

• La fuerza de repulsión de compensa con la de atracción, las partículas permanecen en el estado inicial

• La fuerza de repulsión es menor que la de atracción, las partículas se acercan, r<r₀

2. Las cargas de las partículas son de signo opuesto

• La fuerza eléctrica y la fuerza de atracción gravitaría son del mismo signo, las partículas se acercan, r<r₀

Sistema aislado

Tenemos un sistema aislado de dos partículas bajo la acción de dos fuerzas conservativas: gravitatoria y eléctrica. La energía en la situación inicial es igual a la energía en la situación final. La energía inicial es

${\displaystyle E=-G\frac{m_1{m}_2}{r_0}+\frac{1}{4\pi {\epsilon }_0}\frac{q_1{q}_2}{r_0}}$

y en el instante t es

${\displaystyle E=\frac{1}{2}{m}_1{\left(\frac{d{r}_1}{dt}\right)}^2+\frac{1}{2}{m}_2{\left(\frac{d{r}_2}{dt}\right)}^2-G\frac{m_1{m}_2}{r}+\frac{1}{4\pi {\epsilon }_0}\frac{q_1{q}_2}{r}}$

Igualando ambas energías

${\displaystyle \frac{1}{2}{m}_1{\left(\frac{d{r}_1}{dt}\right)}^2+\frac{1}{2}{m}_2{\left(\frac{d{r}_2}{dt}\right)}^2=\left(G{m}_1{m}_2-\frac{q_1{q}_2}{4\pi {\epsilon }_0}\right)\left(\frac{1}{r}-\frac{1}{r_0}\right)}$

En un sistema aislado de dos partículas interactuantes, si el centro de masas O estaba en reposo, sigue en reposo

${\displaystyle \begin{array}{l}{m}_1{r}_1+m_2{r}_2=0\\ r=r_2-r_1\end{array}\}{r}_2=\frac{m_1}{m_1+m_2}r{r}_1=-\frac{m_2}{m_1+m_2}r}$

Escribimos la ecuación de la conservación de la energía, en términos del vector separación r entre las dos partículas

${\displaystyle \begin{array}{l}\frac{1}{2}\frac{m_1{m}_2}{m_1+m_2}{\left(\frac{dr}{dt}\right)}^2=\left(G{m}_1{m}_2-\frac{q_1{q}_2}{4\pi {\epsilon }_0}\right)\left(\frac{1}{r}-\frac{1}{r_0}\right)\\ {\left(\frac{dr}{dt}\right)}^2=2G\left(m_1+m_2\right)\left(1-\Lambda \right)\left(\frac{1}{r}-\frac{1}{r_0}\right)\Lambda =\frac{q_1{q}_2}{4\pi {\epsilon }_0}\frac{1}{G{m}_1{m}_2}\end{array}}$

El parámetro Λ es el cociente entre la fuerza eléctrica y la fuerza de atracción gravitatoria.

Hacemos el siguiente cambio de escalas x=r/r₀ y τ=t/P

${\displaystyle P^2=\frac{4{\pi }^2{r}_0^3}{G\left(m_1+m_2\right)\left|1-\Lambda \right|}}$

Con este cambio, la ecuación diferencial en r y t se expresa de forma más simple en términos de x y τ

${\displaystyle {\left(\frac{dx}{d\tau }\right)}^2=8{\pi }^2\frac{1-\Lambda }{\left|1-\Lambda \right|}\left(\frac{1}{x}-1\right)}$

• Si Λ<1 las fuerzas atractivas dominan, las partículas se acercan, x≤1

${\displaystyle \frac{dx}{d\tau }=-2\sqrt{2}\pi \sqrt{\frac{1-x}{x}}}$

• Si Λ>1 las fuerzas atractivas dominan, las partículas se alejan, x≥1

${\displaystyle \frac{dx}{d\tau }=2\sqrt{2}\pi \sqrt{\frac{x-1}{x}}}$

Obtenemos las solución de cada una de las ecuaciones diferenciales

Las partículas se acercan

Integramos la ecuación diferencial

${\displaystyle -{\displaystyle \underset{1}{\overset{x}{\int }}\sqrt{\frac{x}{1-x}}}dx=2\sqrt{2}\pi {\displaystyle \underset{0}{\overset{\tau }{\int }}d\tau }}$

Se hace el cambio de variable

${\displaystyle \begin{array}{l}{z}^2=\frac{x}{1-x}x=\frac{z^2}{1+z^2}\\ dx=\frac{2z}{{\left(1+z^2\right)}^2}dz\\ {\displaystyle \int \sqrt{\frac{x}{1-x}}dx=\frac{z}{1+z^2}-\arctan z}\end{array}}$

Se deshace el cambio

${\displaystyle \begin{array}{l}{\sqrt{x(1-x)}-\arctan \sqrt{\frac{x}{1-x}}|}_1^x=2\sqrt{2}\pi ·\tau \\ \sqrt{x(1-x)}-\arctan \sqrt{\frac{x}{1-x}}+\frac{\pi }{2}=2\sqrt{2}\pi ·\tau \end{array}}$

Que es el resultado que hemos obtenido en la página anterior

Intregramos y despejamos τ mediante Math Symbolic

>> syms x;
>> tau=-int('sqrt(x/(1-x))',x,1,x)/(2*sym('sqrt(2)')*pi)
tau =(2^(1/2)*(atan(1/(-x/(x - 1))^(1/2)) - x*(-x/(x - 1))^(1/2) +
 (-x/(x - 1))^(1/2)))/(4*pi)

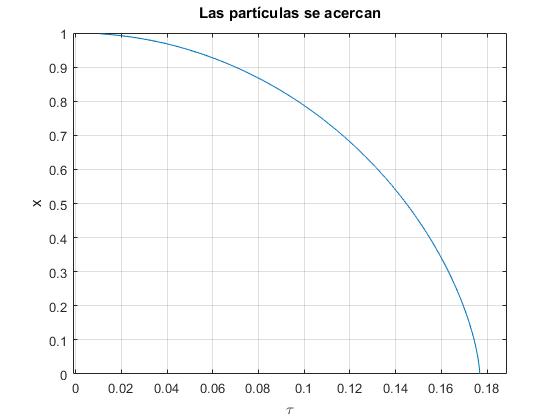
Representamos la función implícita τ=f(x) en el intervalo 0<x<1

>> ezplot(tau,[0,1])
>> ylabel('\tau')
>> title('Las partículas se acercan')
>> grid on
>> view([90 -90]) %gira los ejes

Ejemplo

Un electrón y un protón están inicialmente separados r₀= 1 m. Calcular el tiempo que tardan en chocar r=0.

${\displaystyle \Lambda =\frac{q_1{q}_2}{4\pi {\epsilon }_0}\frac{1}{G{m}_1{m}_2}=\frac{9·{10}^9}{6.67·{10}^{-11}}\frac{1.6·{10}^{-19}·1.6·{10}^{-19}}{9.1·{10}^{-31}·1.6726·{10}^{-27}}=-2.27·{10}^{39}}$

Para x=0, el tiempo adimensional τ es

${\displaystyle \frac{\pi }{2}=2\sqrt{2}\pi ·\tau \tau =\frac{1}{4\sqrt{2}}}$

${\displaystyle P^2=\frac{4{\pi }^2·1^3}{6.67·{10}^{-11}\left(9.1·{10}^{-31}+1.6726·{10}^{-27}\right)·\left(2.27·{10}^{39}+1\right)}}$

El tiempo t es

${\displaystyle t=\frac{1}{4\sqrt{2}}P=0.0698\text{s}}$

>> limit(tau,x,0)
ans =2^(1/2)/8
>> K=-9*10^9*(1.6*10^-19)^2/(6.67*10^-11*9.1*10^-31*1.6726*10^-27)
K =   -2.2695e+39

>> P=sqrt(4*pi^2/(6.67*10^-11*(9.1*10^-31+1.6726*10^-27)*K))
P =    0.3948
>> t=P/(4*sqrt(2))
t=    0.0698

Las partículas se alejan

La solución de la segunda ecuación diferencial es diferente

${\displaystyle {\displaystyle \underset{1}{\overset{x}{\int }}\sqrt{\frac{x}{x-1}}}dx=2\sqrt{2}\pi {\displaystyle \underset{0}{\overset{\tau }{\int }}d\tau }}$

Se hace el cambio de variable

${\displaystyle \begin{array}{l}{z}^2=\frac{x}{x-1}x=\frac{z^2}{z^2-1}\\ dx=-\frac{2z}{{\left(z^2-1\right)}^2}dz\end{array}}$

Se descompone el integrando en la suma de cuatro fracciones

${\displaystyle {\displaystyle \int \frac{-2z^2}{{\left(z^2-1\right)}^2}}dz}$

${\displaystyle \frac{-2z^2}{{\left(z^2-1\right)}^2}=\frac{A}{z-1}+\frac{B}{{\left(z-1\right)}^2}+\frac{C}{z+1}+\frac{D}{{\left(z+1\right)}^2}\{\begin{array}{l}A=-1/2\\ B=-1/2\\ C=1/2\\ D=-1/2\end{array}}$

Tenemos la suma de cuatro integrales

${\displaystyle \begin{array}{l}{\displaystyle \int \frac{-2z^2}{{\left(z^2-1\right)}^2}}dz=-\frac{1}{2}\log \left(z-1\right)+\frac{1}{2}\frac{1}{z-1}+\frac{1}{2}\log \left(z+1\right)+\frac{1}{2}\frac{1}{z+1}=\\ \frac{1}{2}\log \left(\frac{z+1}{z-1}\right)+\frac{z}{z^2-1}\end{array}}$

Se deshace el cambio

${\displaystyle \begin{array}{l}{\frac{1}{2}\log \left(\frac{\sqrt{x}+\sqrt{x-1}}{\sqrt{x}-\sqrt{x-1}}\right)+\sqrt{x(x-1)}|}_1^x=2\sqrt{2}\pi ·\tau \\ \frac{1}{2}\log \left(\frac{\sqrt{x}+\sqrt{x-1}}{\sqrt{x}-\sqrt{x-1}}\right)+\sqrt{x(x-1)}=2\sqrt{2}\pi ·\tau \end{array}}$

>> syms x;
>> tau=int('sqrt(x/(x-1))',x,1,x)/(2*sym('sqrt(2)')*pi)
tau =(2^(1/2)*(atanh(1/(x/(x - 1))^(1/2)) +
 x*(x/(x - 1))^(1/2) - (x/(x - 1))^(1/2)))/(4*pi)
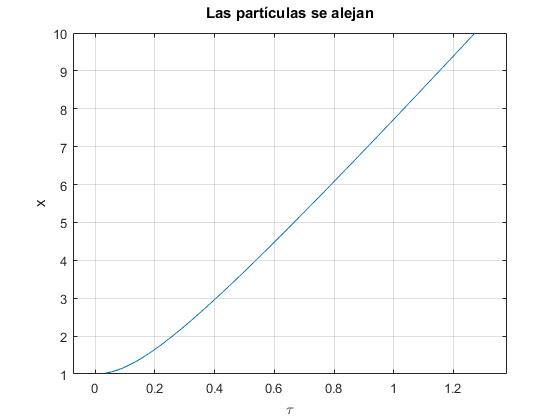
>> ezplot(tau,[1,10])
>> ylabel('\tau')
>> xlabel('x')
>> title('Las partículas se alejan')
>> grid on
>> view([90 -90]) %gira los ejes

Ejemplo

Dos protones están separados inicialmente r₀=10^-14 m. Calcular el tiempo que tardan en alcanzar una separación de r=10^-12 m m

${\displaystyle \Lambda =\frac{q_1{q}_2}{4\pi {\epsilon }_0}\frac{1}{G{m}_1{m}_2}=\frac{9·{10}^9}{6.67·{10}^{-11}}\frac{1.6·{10}^{-19}·1.6·{10}^{-19}}{1.6726·{10}^{-27}·1.6726·{10}^{-27}}=1.23·{10}^{36}}$

Para x=r/r₀=100, el tiempo adimensional τ es

tau_1=subs(tau,x,100)
tau_1 =(2^(1/2)*(atanh(99^(1/2)/10) + 10*99^(1/2)))/(4*pi)
>> double(tau_1)
ans =  11.5344

${\displaystyle \frac{1}{2}\log \left(\frac{10+\sqrt{99}}{10-\sqrt{99}}\right)+\sqrt{100·99}=2\sqrt{2}\pi ·\tau \tau =11.5344}$

${\displaystyle P^2=\frac{4{\pi }^2{\left({10}^{-14}\right)}^3}{6.67·{10}^{-11}\left(1.6726·{10}^{-27}+1.6726·{10}^{-27}\right)·(1.23·{10}^{36}-1)}}$

El tiempo t es

${\displaystyle t=\tau P=7.79·{10}^{-20}\text{s}}$

Referencias

S K Foong. From Moon-fall to motion under inverse square laws. Eur. J. Phys. 29 (2008) 987-1003