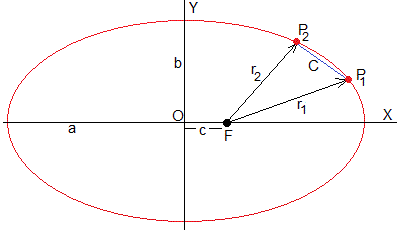
El teorema de Lambert

Trayectorias elípticas

Diferencia de tiempos t₂-t₁

Los instantes t₁ y t₂ se calculan a partir de la ecuación de Kepler para trayectorias elípticas

$\begin{array}{l} t_{1} = \frac{P}{2 π} (E_{1} - ε \sin E_{1}) \\ t_{2} = \frac{P}{2 π} (E_{2} - ε \sin E_{2}) \\ t_{2} - t_{1} = \frac{P}{2 π} (E_{2} - E_{1} - ε (\sin E_{2} - \sin E_{1})) \end{array}$

Donde E₁ es el ángulo que forma el vector posición OP₁ con el eje X y E₂ es el ángulo que forma el vector OP₂ con el eje X. ε<1, es la excentricidad de la elipse.

Utilizamos las relaciones trigonométrics

$\begin{array}{l} {\begin{cases} \sin (A + B) = \sin A \cos B + \sin B \cos A \\ \sin (A - B) = \sin A \cos B - \sin B \cos A \end{cases} \\ \sin (A + B) - \sin (A - B) = 2 \sin B \cos A \end{array}$

Llamando u=A+B y v=A-B

$\begin{array}{l} A = \frac{u + v}{2}, B = \frac{u - v}{2} \\ \sin u - \sin v = 2 \cos (\frac{u + v}{2}) \sin (\frac{u - v}{2}) \end{array}$

El resultado es

$t_{2} - t_{1} = \frac{P}{2 π} {E_{2} - E_{1} - 2 ε \cos (\frac{E_{2} + E_{1}}{2}) \sin (\frac{E_{2} - E_{1}}{2})}$

Distancia C entre los dos posiciones P₁ y P₂

Utilizamos la ecuación de una elipse en términos del ángulo E

$r = a (1 - ε \cos E)$

Calculamos las coordenadas del punto P, x=rcosθ, y=rsinθ en términos del ángulo E

De la relación entre θ y E

$\tan (\frac{θ}{2}) = \sqrt{\frac{1 + ε}{1 - ε}} \tan (\frac{E}{2})$

Hemos obtenido

$\cos θ = \frac{\cos E - ε}{1 - ε \cos E}, \sin θ = \sqrt{1 - \cos^{2} θ} = \sqrt{1 - ε^{2}} \frac{\sin E}{1 - ε \cos E}$

Las coordenadas x e y del punto P son

${\begin{cases} x = a (\cos E - ε) \\ y = a \sqrt{1 - ε^{2}} \sin E \end{cases}$

La longitud de la cuerda C es

$\begin{array}{l} C^{2} = {(x_{2} - x_{1})}^{2} + {(y_{2} - y_{1})}^{2} \\ C^{2} = a^{2} {(\cos E_{2} - \cos E_{1})}^{2} + a^{2} (1 - ε^{2}) {(\sin E_{2} - \sin E_{1})}^{2} \\ C^{2} = 2 a^{2} - 2 a^{2} \cos (E_{2} - E_{1}) - a^{2} ε^{2} {(\sin E_{2} - \sin E_{1})}^{2} \\ C^{2} = 4 a^{2} \sin^{2} (\frac{E_{2} - E_{1}}{2}) - 4 a^{2} ε^{2} \cos^{2} (\frac{E_{2} + E_{1}}{2}) \sin^{2} (\frac{E_{2} - E_{1}}{2}) \\ C^{2} = 4 a^{2} \sin^{2} (\frac{E_{2} - E_{1}}{2}) {1 - ε^{2} \cos^{2} (\frac{E_{2} + E_{1}}{2})} \end{array}$

Suma de las longitudes de los radio vectores, r₁+r₂

$r_{1} + r_{2} = a (1 - ε \cos E_{1}) + a (1 - ε \cos E_{2}) = 2 a (1 - \frac{1}{2} ε (\cos E_{1} + \cos E_{2}))$

Utilizamos las relaciones trigonométricas

$\begin{array}{l} {\begin{cases} \cos (A + B) = \cos A \cos B - \sin A \sin B \\ \cos (A - B) = \cos A \cos B + \sin A \sin B \end{cases} \\ \cos (A + B) + \cos (A - B) = 2 \cos A \cos B \end{array}$

Llamando u=A+B y v=A-B

$\begin{array}{l} A = \frac{u + v}{2}, B = \frac{u - v}{2} \\ \cos u + \cos v = 2 \cos (\frac{u + v}{2}) \cos (\frac{u - v}{2}) \end{array}$

El resultado es

$r_{1} + r_{2} = 2 a {1 - ε \cos (\frac{E_{2} + E_{1}}{2}) \cos (\frac{E_{2} - E_{1}}{2})}$

Relaciones

Los resultados parciales obtenidos son

${\begin{cases} t_{2} - t_{1} = \frac{P}{2 π} {E_{2} - E_{1} - 2 ε \cos (\frac{E_{2} + E_{1}}{2}) \sin (\frac{E_{2} - E_{1}}{2})} \\ C^{2} = 4 a^{2} {1 - ε^{2} \cos^{2} (\frac{E_{2} + E_{1}}{2})} \sin^{2} (\frac{E_{2} - E_{1}}{2}) \\ r_{1} + r_{2} = 2 a {1 - ε \cos (\frac{E_{2} + E_{1}}{2}) \cos (\frac{E_{2} - E_{1}}{2})} \end{cases}$

Para simplificar las expresiones, llamamos

$\begin{array}{l} x = ε \cos (\frac{E_{2} + E_{1}}{2}), y = \frac{E_{2} - E_{1}}{2} \\ {\begin{cases} t_{2} - t_{1} = \frac{P}{2 π} (2 y - 2 x \sin y) \\ C = 2 a \sqrt{1 - x^{2}} \sin y \\ r_{1} + r_{2} = 2 a (1 - x \cos y) \end{cases} \end{array}$

Sumamos y restamos las dos últimas ecuaciones

${\begin{cases} r_{1} + r_{2} + C = 2 a (1 - x \cos y + \sqrt{1 - x^{2}} \sin y) \\ r_{1} + r_{2} - C = 2 a (1 - x \cos y - \sqrt{1 - x^{2}} \sin y) \end{cases}$

Hacemos un nuevo cambio de variable

$\begin{array}{l} x = \cos (\frac{α + β}{2}), y = \frac{α - β}{2} \\ {\begin{cases} t_{2} - t_{1} = \frac{P}{2 π} (α - β - 2 \cos (\frac{α + δ}{2}) \sin (\frac{α - β}{2})) \\ r_{1} + r_{2} + C = 2 a (1 - \cos (\frac{α + β}{2}) \cos (\frac{α - β}{2}) + \sin (\frac{α + β}{2}) \sin (\frac{α - β}{2})) \\ r_{1} + r_{2} - C = 2 a (1 - \cos (\frac{α + β}{2}) \cos (\frac{α - β}{2}) - \sin (\frac{α + β}{2}) \sin (\frac{α - β}{2})) \end{cases} \end{array}$

Utilizando la relaciones trigonométricas

$\begin{array}{l} {\begin{cases} \cos (A + B) = \cos A \cos B - \sin A \sin B \\ \cos (A - B) = \cos A \cos B + \sin A \sin B \end{cases} \\ \cos (A - B) - \cos (A + B) = 2 \sin A \sin B \end{array}$

Llamando u=A+B y v=A-B

$\begin{array}{l} A = \frac{u + v}{2}, B = \frac{u - v}{2} \\ \cos v - \cos u = 2 \sin (\frac{u + v}{2}) \sin (\frac{u - v}{2}) \end{array}$

El resultado es

$\begin{array}{l} {\begin{cases} r_{1} + r_{2} + C = 2 a (1 - \frac{1}{2} (\cos β + \cos α) + \frac{1}{2} (\cos β - \cos α)) \\ r_{1} + r_{2} - C = 2 a (1 - \frac{1}{2} (\cos β + \cos α) - \frac{1}{2} (\cos β - \cos α)) \end{cases} \\ {\begin{cases} r_{1} + r_{2} + C = 2 a (1 - \cos α) = 4 a \sin^{2} \frac{α}{2} \\ r_{1} + r_{2} - C = 2 a (1 - \cos β) = 4 a \sin^{2} \frac{β}{2} \end{cases} \end{array}$

Se ha empleado la relación

$\cos (2 θ) = \cos^{2} θ - \sin^{2} θ$

Conocidos la longitud de los radio vectores, r₁ y r₂ y la longitud de la cuerda C, los ángulos α y β valen

${\begin{cases} \sin \frac{α}{2} = \frac{1}{2} \sqrt{\frac{r_{1} + r_{2} + C}{a}} \\ \sin \frac{β}{2} = \frac{1}{2} \sqrt{\frac{r_{1} + r_{2} - C}{a}} \end{cases}$

Para calcular el intervalo de tiempo en función de los ángulos α y β utilizamos la relación trigonométrica, sinu-sinv. El resultado final es

$t_{2} - t_{1} = \frac{P}{2 π} (α - β - (\sin α - \sin β))$

El intervalo de tiempo t₂-t₁ depende de los ángulos α y β, es decir, de r₁+r₂ y la longitud C

Ejemplo

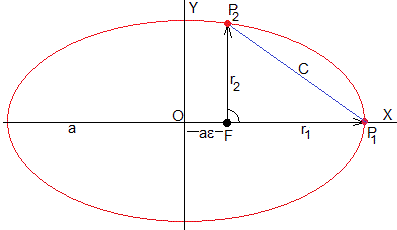
La posición P₁ es θ₁=0
La posición P₂ es θ₂=π/2

La ecuación de la elipse es

$r = \frac{d}{1 + ε \cos θ} = \frac{a (1 - ε^{2})}{1 + ε \cos θ}$

La longitud de los radio vectores es

${\begin{cases} θ_{1} = 0, r_{1} = a (1 - ε) \\ θ_{2} = \frac{π}{2}, r_{2} = a (1 - ε^{2}) \end{cases}$

La distancia C entre los dos puntos P₁ y P₂ es

$C = \sqrt{r_{1}^{2} + r_{2}^{2}} = a (1 - ε) \sqrt{1 + {(1 + ε)}^{2}} = a (1 - ε) \sqrt{2 + 2 ε + ε^{2}}$

De otro modo. La relación entre los ángulos θ y E es

$\begin{array}{l} \tan (\frac{E}{2}) = \sqrt{\frac{1 - ε}{1 + ε}} \tan (\frac{θ}{2}) \\ {\begin{cases} θ_{1} = 0, E_{1} = 0 \\ θ_{2} = \frac{π}{2}, \tan (\frac{E_{2}}{2}) = \sqrt{\frac{1 - ε}{1 + ε}} \end{cases} \end{array}$

La longitud de la cuerda C vale

$\begin{array}{l} x = ε \cos (\frac{E_{2}}{2}), y = \frac{E_{2}}{2} \\ C = 2 a \sqrt{1 - x^{2}} \sin y \end{array}$

Teniendo en cuenta las relaciones trigonométricas

$\cos θ = \frac{1}{\sqrt{1 + \tan^{2} θ}}, \sin θ = \frac{\tan θ}{\sqrt{1 + \tan^{2} θ}}$

El resultado es

$\begin{array}{l} x = ε \cos (\frac{E_{2}}{2}) = ε \sqrt{\frac{1 + ε}{2}} \\ \sin (\frac{E_{2}}{2}) = \sqrt{\frac{1 - ε}{2}} \\ C = 2 a \sqrt{1 - ε^{2} \frac{1 + ε}{2}} \sqrt{\frac{1 - ε}{2}} = a \sqrt{(2 - ε^{2} - ε^{3}) (1 - ε)} = a (1 - ε) \sqrt{2 + 2 ε + ε^{2}} \end{array}$

Conocidos r₂+r₁ y C, los ángulos α y β son

$\begin{array}{l} {\begin{cases} C = a (1 - ε) \sqrt{2 + 2 ε + ε^{2}} \\ r_{1} + r_{2} = a (1 - ε) (2 + ε) \end{cases} \\ {\begin{cases} \sin \frac{α}{2} = \frac{1}{2} \sqrt{1 - ε} \sqrt{2 + ε + \sqrt{2 + 2 ε + ε^{2}}} \\ \sin \frac{β}{2} = \frac{1}{2} \sqrt{1 - ε} \sqrt{2 + ε - \sqrt{2 + 2 ε + ε^{2}}} \end{cases} \end{array}$

El intervalo de tiempo es

$t_{2} - t_{1} = \frac{P}{2 π} (α - β - (\sin α - \sin β))$

Calculamos cosα y cosβ, empleando las relaciones trigonométricas

\begin{array}{l} \cos α = \cos^{2} (\frac{α}{2}) - \sin^{2} (\frac{α}{2}) = 1 - 2 \sin^{2} (\frac{α}{2}) \\ \cos α = 1 - \frac{1}{2} (1 - ε) (2 + ε + \sqrt{2 + 2 ε + ε^{2}}) \\ \cos β = 1 - \frac{1}{2} (1 - ε) (2 + ε - \sqrt{2 + 2 ε + ε^{2}}) \end{array}

El producto cosα·cosβ es

$\cos α \cos β = \frac{- 1 + ε + ε^{2} + ε^{3}}{2}$

Calculamos sinα y sinβ, empleando las relaciones trigonométricas

$\begin{array}{l} \sin α = 2 \sin (\frac{α}{2}) \cos (\frac{α}{2}) = 2 \sin (\frac{α}{2}) \sqrt{1 - \sin^{2} (\frac{α}{2})} \\ \sin α = \sqrt{1 - ε} \sqrt{2 + ε + \sqrt{2 + 2 ε + ε^{2}}} \sqrt{1 - \frac{1}{4} (1 - ε) (2 + ε + \sqrt{2 + 2 ε + ε^{2}})} = \\ \sqrt{1 - ε} \sqrt{2 + ε + \sqrt{2 + 2 ε + ε^{2}} - \frac{1}{4} (1 - ε) {(2 + ε + \sqrt{2 + 2 ε + ε^{2}})}^{2}} \\ \sin α = \sqrt{\frac{1 - ε^{2}}{2}} \sqrt{ε^{2} + ε + 1 + ε \sqrt{2 + 2 ε + ε^{2}}} \\ \sin β = \sqrt{\frac{1 - ε^{2}}{2}} \sqrt{ε^{2} + ε + 1 - ε \sqrt{2 + 2 ε + ε^{2}}} \end{array}$

El producto sinα·sinβ es

$\sin α \sin β = \frac{1 - ε^{2}}{2} \sqrt{{(ε^{2} + ε + 1)}^{2} - ε^{2} (2 + 2 ε + ε^{2})} = \frac{1 - ε^{2}}{2} (1 + ε) = \frac{1 + ε - ε^{2} - ε^{3}}{2}$

El coseno de la diferencia de dos ángulos es

$\begin{array}{l} \cos (α - β) = \cos α \cos β + \sin α \sin β \\ \cos (α - β) = ε \\ α - β = \arccos (ε) \end{array}$

Elevamos al cuadrado la diferencia, sinα-sinβ

$\begin{array}{l} {(\sin α - \sin β)}^{2} = \sin^{2} α + \sin^{2} β - 2 \sin α \sin β = \\ (\frac{1 - ε^{2}}{2}) (ε^{2} + ε + 1 + ε \sqrt{2 + 2 ε + ε^{2}}) + (\frac{1 - ε^{2}}{2}) (ε^{2} + ε + 1 - ε \sqrt{2 + 2 ε + ε^{2}}) - 2 \frac{1 + ε - ε^{2} - ε^{3}}{2} = \\ (1 - ε^{2}) (ε^{2} + ε + 1) - (1 + ε - ε^{2} - ε^{3}) = ε^{2} (1 - ε^{2}) \\ \sin α - \sin β = ε \sqrt{1 - ε^{2}} \end{array}$

El resultado final es

$t_{2} - t_{1} = \frac{P}{2 π} (\arccos ε - ε \sqrt{1 - ε^{2}})$

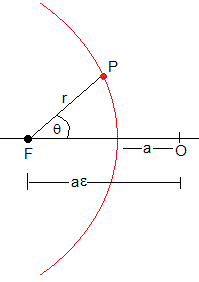
Trayectorias parabólicas

La trayectoria parabólica es una trayectoria elíptica cuyo semieje mayor a tiende a infinito. Entonces los ángulos α y β son pequeños y se pueden aproximar

${\begin{cases} \frac{α}{2} \approx \frac{1}{2} \sqrt{\frac{r_{1} + r_{2} + C}{a}} \\ \frac{β}{2} \approx \frac{1}{2} \sqrt{\frac{r_{1} + r_{2} - C}{a}} \end{cases}$

Desarrollamos en serie la función sin(x) tomando los dos primeros términos

>> syms x;
>> taylor(sin(x))
ans =x^5/120 - x^3/6 + x

$\sin x \approx x - \frac{x^{3}}{6}$

La diferencia de tiempos es aproximadamente

$\begin{array}{l} t_{2} - t_{1} = \frac{P}{2 π} (α - β - (\sin α - \sin β)) \approx \frac{P}{2 π} (α - β - (α - \frac{α^{3}}{6} - β + \frac{β^{3}}{6})) \\ t_{2} - t_{1} \approx \frac{P}{2 π} (\frac{α^{3}}{6} - \frac{β^{3}}{6}) \end{array}$

El periodo o el tiempo que tarda el cuerpo en describir una trayectoria elíptica de semieje a es

$P^{2} = 4 π^{2} \frac{a^{3}}{G M}$

El intervalo de tiempos es independiente del semieje a de la elipse, cuando a es grande

$\begin{array}{l} t_{2} - t_{1} \approx \frac{a^{3 / 2}}{6 \sqrt{G M}} {{(\frac{r_{1} + r_{2} + C}{a})}^{3 / 2} - {(\frac{r_{1} + r_{2} - C}{a})}^{3 / 2}} \\ t_{2} - t_{1} \approx \frac{1}{6 \sqrt{G M}} {{(r_{1} + r_{2} + C)}^{3 / 2} - {(r_{1} + r_{2} - C)}^{3 / 2}} \end{array}$

Trayectorias hiperbólicas

Diferencia de tiempos t₂-t₁

Los instantes t₁ y t₂ se calculan a partir de la ecuación de Kepler para trayectorias hiperbólicas

$\begin{array}{l} t_{1} = \frac{L^{3}}{{(ε^{2} - 1)}^{3 / 2} G^{2} M^{2} m^{3}} (ε \sinh F_{1} - F_{1}) \\ t_{2} = \frac{L^{3}}{{(ε^{2} - 1)}^{3 / 2} G^{2} M^{2} m^{3}} (ε \sinh F_{2} - F_{2}) \\ t_{2} - t_{1} = \frac{L^{3}}{{(ε^{2} - 1)}^{3 / 2} G^{2} M^{2} m^{3}} (ε (\sinh F_{2} - \sinh F_{1}) - (F_{2} - F_{1})) \end{array}$

Donde F₁ es el ángulo que forma el vector posición OP₁ con el eje X y F₂ es el ángulo que forma el vector OP₂ con el eje X. ε>1, es la excentricidad de la hipérbola.

Utilizamos las relaciones trigonométrics

$\begin{array}{l} {\begin{cases} \sinh (A + B) = \sinh A \cosh B + \sinh B \cosh A \\ \sinh (A - B) = \sinh A \cosh B - \sinh B \cosh A \end{cases} \\ \sinh (A + B) - \sinh (A - B) = 2 \sinh B \cosh A \end{array}$

Llamando u=A+B y v=A-B

$\begin{array}{l} A = \frac{u + v}{2}, B = \frac{u - v}{2} \\ \sinh u - \sinh v = 2 \cosh (\frac{u + v}{2}) \sinh (\frac{u - v}{2}) \end{array}$

El resultado es

$t_{2} - t_{1} = \frac{L^{3}}{{(ε^{2} - 1)}^{3 / 2} G^{2} M^{2} m^{3}} {2 ε \cosh (\frac{F_{2} + F_{1}}{2}) \sinh (\frac{F_{2} - F_{1}}{2}) - (F_{2} - F_{1})}$

Distancia C entre los dos posiciones P₁ y P₂

Utilizamos la ecuación de una hipérbola en términos del ángulo E

$r = a (ε \cosh F - 1)$

Calculamos las coordenadas del punto P, x=rcosθ, y=rsinθ en términos del ángulo F

De la relación entre θ y F

$\tan (\frac{θ}{2}) = \sqrt{\frac{ε + 1}{ε - 1}} \tan (\frac{F}{2})$

Hemos obtenido

$\cos θ = \frac{ε - \cosh F}{ε \cosh F - 1}, \sin θ = \sqrt{1 - \cos^{2} θ} = \sqrt{1 - ε^{2}} \frac{\sinh F}{ε \cosh F - 1}$

Las coordenadas x e y del punto P son

${\begin{cases} x = a (ε - \cosh F) \\ y = a \sqrt{1 - ε^{2}} \sinh F \end{cases}$

Hemos empleado la relación

$\cosh^{2} x - \sinh^{2} x = 1$

La longitud de la cuerda C es

$\begin{array}{l} C^{2} = {(x_{2} - x_{1})}^{2} + {(y_{2} - y_{1})}^{2} \\ C^{2} = a^{2} {(\cosh F_{2} - \cosh F_{1})}^{2} + a^{2} (ε^{2} - 1) {(\sinh F_{2} - \sinh F_{1})}^{2} \\ C^{2} = 4 a^{2} \sinh^{2} (\frac{F_{2} + F_{1}}{2}) \sinh^{2} (\frac{F_{2} - F_{1}}{2}) + 4 a^{2} (ε^{2} - 1) \cosh^{2} (\frac{F_{2} + F_{1}}{2}) \sinh^{2} (\frac{F_{2} - F_{1}}{2}) \\ C^{2} = 4 a^{2} \sinh^{2} (\frac{F_{2} + F_{1}}{2}) {\sinh^{2} (\frac{F_{2} - F_{1}}{2}) + (ε^{2} - 1) \cosh^{2} (\frac{F_{2} + F_{1}}{2})} \\ C^{2} = 4 a^{2} \sinh^{2} (\frac{F_{2} + F_{1}}{2}) {\cosh^{2} (\frac{F_{2} + F_{1}}{2}) - 1} \end{array}$

Hemos empleado la relación

$\cosh u - \cosh v = 2 \sinh (\frac{u + v}{2}) \sinh (\frac{u - v}{2})$

cuya demostración es similar a sinhu-sinhv

Suma de las longitudes de los radio vectores, r₁+r₂

$r_{1} + r_{2} = a (ε \cosh F_{1} - 1) + a (ε \cosh F_{2} - 1) = 2 a (\frac{1}{2} ε (\cosh F_{1} + \cosh F_{2}) - 1)$

Utilizando la relación

$\cosh u + \cosh v = 2 \cosh (\frac{u + v}{2}) \cosh (\frac{u - v}{2})$

El resultado es

$r_{1} + r_{2} = 2 a {ε \cosh (\frac{F_{2} + F_{1}}{2}) \cosh (\frac{F_{2} - F_{1}}{2}) - 1}$

Relaciones

Los resultados parciales obtenidos son

${\begin{cases} t_{2} - t_{1} = \frac{L^{3}}{{(ε^{2} - 1)}^{3 / 2} G^{2} M^{2} m^{3}} {2 ε \cosh (\frac{F_{2} + F_{1}}{2}) \sinh (\frac{F_{2} - F_{1}}{2}) - (F_{2} - F_{1})} \\ C^{2} = 4 a^{2} \sinh^{2} (\frac{F_{2} + F_{1}}{2}) {\cosh^{2} (\frac{F_{2} + F_{1}}{2}) - 1} \\ r_{1} + r_{2} = 2 a {ε \cosh (\frac{F_{2} + F_{1}}{2}) \cosh (\frac{F_{2} - F_{1}}{2}) - 1} \end{cases}$

Para simplificar las expresiones, llamamos

$\begin{array}{l} x = ε \cosh (\frac{F_{2} + F_{1}}{2}), y = \frac{F_{2} - F_{1}}{2} \\ {\begin{cases} t_{2} - t_{1} = \frac{L^{3}}{{(ε^{2} - 1)}^{3 / 2} G^{2} M^{2} m^{3}} (2 x \sinh y - 2 y) \\ C = 2 a \sqrt{x^{2} - 1} \sinh y \\ r_{1} + r_{2} = 2 a (x \cosh y - 1) \end{cases} \end{array}$

Sumamos y restamos las dos últimas ecuaciones

${\begin{cases} r_{1} + r_{2} + C = 2 a (x \cosh y - 1 + \sqrt{x^{2} - 1} \sinh y) \\ r_{1} + r_{2} + C = 2 a (x \cosh y - 1 - \sqrt{x^{2} - 1} \sinh y) \end{cases}$

Hacemos un nuevo cambio de variable

$\begin{array}{l} x = \cosh (\frac{α + β}{2}), y = \frac{α - β}{2} \\ {\begin{cases} t_{2} - t_{1} = \frac{L^{3}}{{(ε^{2} - 1)}^{3 / 2} G^{2} M^{2} m^{3}} (2 \cosh (\frac{α + δ}{2}) \sinh (\frac{α - β}{2}) - (α - β)) \\ r_{1} + r_{2} + C = 2 a (\cosh (\frac{α + β}{2}) \cosh (\frac{α - β}{2}) + \sinh (\frac{α + β}{2}) \sinh (\frac{α - β}{2}) - 1) \\ r_{1} + r_{2} - C = 2 a (\cosh (\frac{α + β}{2}) \cosh (\frac{α - β}{2}) - \sinh (\frac{α + β}{2}) \sinh (\frac{α - β}{2}) - 1) \end{cases} \end{array}$

que se simplifican, teniendo en cuenta las relaciones coshu+coshv y coshu-coshv

${\begin{cases} r_{1} + r_{2} + C = 2 a (\frac{1}{2} (\cosh α + \cosh β) + \frac{1}{2} (\cosh α - \cosh β) - 1) \\ r_{1} + r_{2} - C = 2 a (\frac{1}{2} (\cosh α + \cosh β) - \frac{1}{2} (\cosh α - \cosh β) - 1) \end{cases}$

El resultado es

${\begin{cases} r_{1} + r_{2} + C = 2 a (\cosh α - 1) = 4 a \sinh^{2} (\frac{α}{2}) \\ r_{1} + r_{2} - C = 2 a (\cosh β - 1) = 4 a \sinh^{2} (\frac{β}{2}) \end{cases}$

Se ha utilizado la relación

$\cosh (2 x) = \cosh^{2} x + \sinh^{2} x$

Conocidos la longitud de los radio vectores, r₁ y r₂ y la longitud de la cuerda C, los ángulos α y β valen

${\begin{cases} \sinh \frac{α}{2} = \frac{1}{2} \sqrt{\frac{r_{1} + r_{2} + C}{a}} \\ \sinh \frac{β}{2} = \frac{1}{2} \sqrt{\frac{r_{1} + r_{2} - C}{a}} \end{cases}$

Para calcular el intervalo de tiempo en función de los ángulos α y β utilizamos la relación sinhu-sinhv. El resultado final es

$t_{2} - t_{1} = \frac{L^{3}}{{(ε^{2} - 1)}^{3 / 2} G^{2} M^{2} m^{3}} (\sinh α - \sinh β - (α - β))$

El intervalo de tiempo t₂-t₁ depende de los ángulos α y β, es decir, de r₁+r₂ y la longitud C

Referencias

Victor G. Szebehely, Hans Mark. Adventures in Celestial Mechanics. Wiley-VCH (2004), pp. 115-123