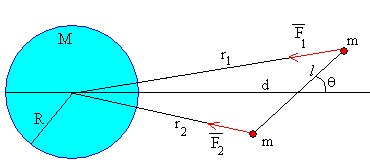
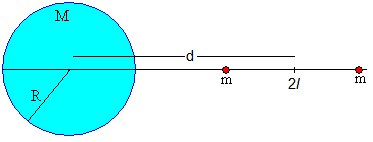
La masa de la Tierra es M y su radio es R. En el espacio hay una varilla de masa despreciable de longitud 2l cuyo centro dista d del centro de la Tierra. En los extremos de la varilla hay dos masas m puntuales iguales. El sistema puede oscilar libremente en el plano de la figura alrededor del centro de masas de la varilla.

Las masas puntuales distan del centro de la Tierra r₁ y r₂ respectivamente

${\displaystyle \begin{array}{l}{r}_1^2={\left(d+l·\cos \theta \right)}^2+{\left(l·\text{sin}\theta \right)}^2=d^2+l^2+2lR\cos \theta \\ r_2^2={\left(d-l·\cos \theta \right)}^2+{\left(l·\text{sin}\theta \right)}^2=d^2+l^2-2lR\cos \theta \end{array}}$

Las fuerzas que ejerce la Tierra sobre cada una de las masas puntuales tienen por módulo

${\displaystyle F_1=G\frac{Mm}{r_1^2}{F}_2=G\frac{Mm}{r_2^2}}$

la dirección es a lo largo de la recta que une el centro de la Tierra y cada una de las masas puntuales, y de sentido hacia el centro de la Tierra.

El momento de las fuerzas $\overrightarrow{F_1}$ y $\overrightarrow{F_2}$ respecto del centro de la varilla es

M=F₁·l·sin(θ-α₁)-F₂·l·sin(θ+α₂)

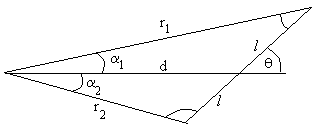
Aplicando el teorema del seno

${\displaystyle \frac{r_1}{\text{sin(180-}\theta \text{)}}=\frac{d}{\text{sin}(\theta -{\alpha }_1)}\frac{r_2}{\text{sin}\theta }=\frac{d}{\text{sin}(180-\theta +{\alpha }_2)}}$

La ecuación del movimiento de rotación alrededor del centro de la varilla es

${\displaystyle I\frac{d^2\theta }{d{t}^2}=G\frac{Mm}{r_1^2}l\frac{d\text{sin}\theta }{r_1}-\frac{Mm}{r_2^2}l\frac{d\text{sin}\theta }{r_2}}$

El momento de inercia de las dos masas puntuales, respecto del eje de rotación perpendicular a la varilla y que pasa por su c.m. es  I=2ml²

${\displaystyle \frac{d^2\theta }{d{t}^2}=\frac{GM·d·\text{sin}\theta }{2l}\left(\frac{1}{r_1^3}-\frac{1}{r_2^3}\right)}$

Se resuelve la ecuación diferencial del movimiento por procedimientos numéricos con las siguientes condiciones iniciales: en el instante t=0, θ=π/6, dθ/dt=0

Convertimos la ecuación diferencial en otra más manejable tomando como unidad el radio de la Tierra, R=6.37·10⁶ m

${\displaystyle \frac{d^2\theta }{d{t}^2}=\frac{GM}{R^3}\frac{\left(d/R\right)\sin \theta }{2\left(l/R\right)}\left(\frac{1}{{\left(r_1/R\right)}^3}-\frac{1}{{\left(r_2/R\right)}^3}\right)}$

Definimos la función pendulo_marea del sistema de dos ecuaciones diferenciales de primer orden, donde x(1) representará los sucesivos valores de la variable θ y x(2) representará a la derivada dθ/dt.

Resolvemos la ecuación diferencial mediante el procedimiento ode45 de MATLAB

function pendulo_marea
    r=2; %distancia al centro
    lon=0.5; %longitud del péndulo
    [t,x]=ode45(@pendulo_marea,[0,20000],[pi/6, 0]);
    plot(t,x(:,1),'r')
    grid on
    xlabel('t')
    ylabel('ángulo');
    title('Péndulo marea')

    function y=pendulo_marea(~,x)
        r1=1.0+lon^2/r^2-2*lon*cos(x(1))/r;
        r2=1.0+lon^2/r^2+2*lon*cos(x(1))/r;
        y=[x(2); -(1.543e-6*sin(x(1))/(2*lon*r^2))*(1.0/r1^1.5-1.0/r2^1.5)];
    end
end

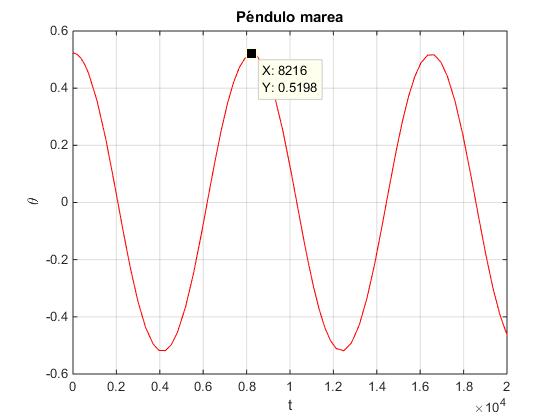
El periodo es aproximadamente 8287 s

Aproximaciones

Supongamos que la longitud de la varilla 2l es pequeña en comparación con la distancia d entre el centro de la Tierra y el c.m. de la varilla.

${\displaystyle \begin{array}{l}\frac{1}{r_1^3}-\frac{1}{r_2^3}=\frac{1}{{\left(d^2+l^2+2ld\cos \theta \right)}^{3/2}}-\frac{1}{{\left(d^2+l^2-2ld\cos \theta \right)}^{3/2}}\approx \\ \frac{1}{d^3{\left(1+2\frac{l}{d}\cos \theta \right)}^{3/2}}-\frac{1}{d^3{\left(1-2\frac{l}{d}\cos \theta \right)}^{3/2}}\end{array}}$

El cociente l/d es pequeño frente a la unidad

>> syms x;
>> f=1/(1+x)^(3/2)-1/(1-x)^(3/2);
>> taylor(f,x)
ans =- 3*x - (35*x^3)/8 - (693*x^5)/128

La ecuación diferencial del movimiento se convierte en otra más simple

${\displaystyle \begin{array}{l}\frac{1}{r_1^3}-\frac{1}{r_2^3}\approx \frac{-3}{d^3}\left(2\frac{l}{d}\cos \theta \right)\\ \frac{d^2\theta }{d{t}^2}=-3\frac{GM}{d^3}\text{sin}\theta ·\cos \theta \end{array}}$

o bien

${\displaystyle \frac{d^2(2\theta )}{d{t}^2}+\frac{3GM}{d^3}\text{sin(2}\theta )=0}$

Esta es una ecuación similar a la del péndulo simple, en vez del ángulo θ, que hace el hilo con la vertical aparece el ángulo 2θ.

Suponiendo que el péndulo oscila con una pequeña amplitud angular, aproximamos sin(2θ)≈(2θ). Obtenemos la ecuación diferencial de un MAS

${\displaystyle \frac{d^2(2\theta )}{d{t}^2}+\frac{3GM·}{d^3}\text{(2}\theta )=0}$

de periodo

${\displaystyle P=\frac{2\pi }{\omega }=2\pi \sqrt{\frac{d^3}{3GM}}}$

El periodo es independiente de la longitud l del péndulo, esto indica que las fuerzas de marea se manifiestan también en sistemas cuyo tamaño es pequeño.

Si el péndulo se coloca en la superficie de la Tierra d=6370 km, M=5.98·10²⁴ kg, G=6.67·10^-11 Nm²/kg²

El periodo P=2920.2 s=48.7 min

Equilibrio y estabilidad

Energía potencial del sistema formado por las dos masas puntuales unidas por una varilla de masa de longitud 2l de masa despreciable

${\displaystyle \begin{array}{l}{E}_p(\theta )=-G\frac{Mm}{r_1}-G\frac{Mm}{r_2}=-GMm\left(\frac{1}{\sqrt{d^2+l^2+2ld\cos \theta }}+\frac{1}{\sqrt{d^2+l^2-2ld\cos \theta }}\right)\\ \approx -\frac{GMm}{d}\left(\frac{1}{\sqrt{1+2\frac{l}{d}\cos \theta }}+\frac{1}{\sqrt{1-2\frac{l}{d}\cos \theta }}\right)\end{array}}$

El cociente l/d es pequeño frente a la unidad

>> syms x;
>> f=1/sqrt(1+x)+1/sqrt(1-x);
>> taylor(f,x)
 ans =(35*x^4)/64 + (3*x^2)/4 + 2

${\displaystyle E_p(\theta )\approx -\frac{GMm}{d}\left(2+\frac{3}{4}{\left(2\frac{l}{d}\cos \theta \right)}^2\right)=-\frac{GMm}{d}\left(2+3{\left(\frac{l}{d}\right)}^2{\cos }^2\theta \right)}$

Representamos la función E_p(θ)

k=0.1;
fplot(@(x) -(2+3*k^2*cos(x).^2),[-pi/6,2*pi/3])
grid on
set(gca,'XTick',-pi/6:pi/6:2*pi/3)
set(gca,'XTickLabel',{'-\pi/6','0','\pi/6','\pi/3','\pi/2','2\pi/3'})
xlabel('\theta')
ylabel('E_p(\theta)')
title('Energía potencial')

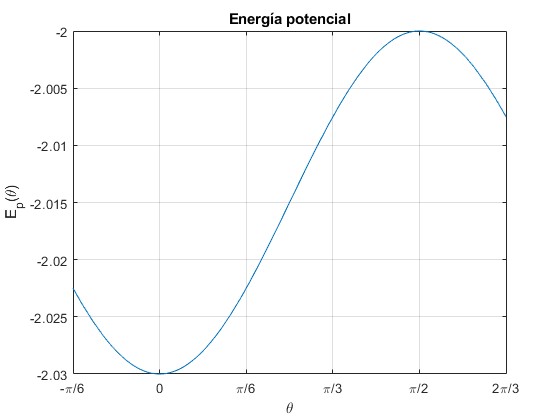
El mínimo de energía potencial se calcula derivando respecto de θ e igualando a cero

${\displaystyle \frac{d{E}_p}{d\theta }\approx -6\frac{GMm}{d}{\left(\frac{l}{d}\right)}^2\cos \theta \sin \theta =0}$

Tiene dos soluciones θ=0, y θ=π/2, tal como apreciamos en la representación gráfica

Calculamos la derivada segunda

${\displaystyle \begin{array}{l}\frac{d^2{E}_p}{d{\theta }^2}=-6\frac{GMm}{d}{\left(\frac{l}{d}\right)}^2\left\{-{\sin }^2\theta +{\cos }^2\theta \right\}\\ \frac{d^2{E}_p}{d{\theta }^2}\{\begin{array}{l}>\mathrm{0,}\theta =0\\ <\mathrm{0,}\theta =\frac{\pi }{2}\end{array}\end{array}}$

La energía potencial tiene un mínimo para θ=0

Ecuación del movimiento

Para oscilaciones de pequeña amplitud

${\displaystyle \begin{array}{l}{\cos }^2\theta \approx 1-{\theta }^2\\ E_p(\theta )\approx 3\frac{GMm}{R}{\left(\frac{l}{d}\right)}^2{\theta }^2+\text{cte}\end{array}}$

La energía cinética, excluyendo la energía cinética del c.m. que es constante

${\displaystyle E_k=2\frac{1}{2}m{\left(l\frac{d\theta }{dt}\right)}^2}$

La Lagrangiana y la ecuación del movimiento son

${\displaystyle \begin{array}{l}L=E_k-E_p=m{\left(l\frac{d\theta }{dt}\right)}^2-3\frac{GMm}{d^3}{l}^2{\theta }^2+\text{cte}\\ \frac{d}{dt}\left(\frac{\partial L}{\partial \dot{\theta }}\right)-\frac{\partial L}{\partial \theta }=0\\ 2m{l}^2\frac{d^2\theta }{d{t}^2}+6\frac{GMm}{d^3}{l}^2\theta =0\\ \frac{d^2\theta }{d{t}^2}+3\frac{GM}{d^3}\theta =0\end{array}}$

La misma ecuación que hemos obtenido en el apartado anterior

Referencias

Grǿn Ǿ. A tidal force pendulum. Am. J. Phys. 51 (5) May 1983, pp. 429-431

Sidney B. Cahn, Boris E. Nadgorny. A guide to physics problems, part 1. Mechanics, Relativity, and Electrodynamics.. Kluwer Academic Publishers, 2004. Problem 1.17