Periodos

La fuerza de atracción es central y conservativa, la energía y el momento angular son constantes

${\displaystyle \begin{array}{l}E=\frac{1}{2}m\left\{{\left(\frac{dr}{dt}\right)}^2+r^2{\left(\frac{d\theta }{dt}\right)}^2\right\}-\frac{GMm}{r}\hfill \\ L=m{r}^2\frac{d\theta }{dt}\hfill \end{array}}$

La conservación de la energía se escribe

${\displaystyle E=\frac{1}{2}m{\left(\frac{dr}{dt}\right)}^2+\frac{L^2}{2m{r}^2}-\frac{GMm}{r}}$

Un cuerpo celeste describe una trayectoria elíptica cuando su energía E<0. La distancia más cercana r₁ y más alejada r₂ del centro fijo de fuerzas se obtiene cuando la componente radial de la velocidad dr/dt. En esas posiciones dicha componente cambia de sentido.

${\displaystyle \begin{array}{l}E=\frac{L^2}{2m{r}^2}-\frac{GMm}{r}\\ 2\frac{E}{m}{r}^2+2GMr-\frac{L^2}{m^2}=\mathrm{0,}E<0\\ -a{r}^2+br-c=0\\ r_1=\frac{b-\sqrt{b^2-4ac}}{2a}=\frac{-GM-\sqrt{G^2{M}^2+2E{L}^2/m^3}}{2E/m}\\ r_2=\frac{b+\sqrt{b^2-4ac}}{2a}=\frac{-GM+\sqrt{G^2{M}^2+2E{L}^2/m^3}}{2E/m}\end{array}}$

Periodo radial

En la ecuación de la energía despejamos dr/dt

${\displaystyle \begin{array}{l}\frac{dr}{dt}=\sqrt{\frac{2}{m}\left(E-\frac{L^2}{2m{r}^2}+\frac{GMm}{r}\right)}\\ dt=\frac{r·dr}{\sqrt{\frac{2E}{m}{r}^2+2GMr-\frac{L^2}{m^2}}}\end{array}}$

Como E<0, denominamos a=-2E/m, b=2GM, c=L²/m² y x=r. Calculamos la integral

${\displaystyle \begin{array}{l}{\displaystyle \int \frac{x·dx}{\sqrt{-a{x}^2+bx-c}}=-\frac{1}{2a}{\displaystyle \int \frac{(-2ax+b)·dx}{\sqrt{-a{x}^2+bx-c}}}}+\frac{b}{2a}{\displaystyle \int \frac{dx}{\sqrt{-a{x}^2+bx-c}}}=\\ -\frac{1}{a}\sqrt{-a{x}^2+bx-c}+\frac{b}{2a}{\displaystyle \int \frac{dx}{\sqrt{a\left\{\frac{-c}{a}+\frac{b^2}{4a^2}-{\left(x-\frac{b}{2a}\right)}^2\right\}}}}\end{array}}$

Hacemos el cambio de variable

${\displaystyle \begin{array}{l}x-\frac{b}{2a}=\sqrt{-\frac{c}{a}+\frac{b^2}{4a^2}}\sin \xi \\ dx=\sqrt{-\frac{c}{a}+\frac{b^2}{4a^2}}\cos \xi ·d\xi \end{array}}$

El resultado es

${\displaystyle \begin{array}{l}{\displaystyle \int \frac{x·dx}{\sqrt{-a{x}^2+bx-c}}}=-\frac{1}{a}\sqrt{-a{x}^2+bx-c}+\frac{b}{2a^{3/2}}\xi =\\ -\frac{1}{a}\sqrt{-a{x}^2+bx-c}+\frac{b}{2a^{3/2}}\arcsin \left(\frac{2ax-b}{\sqrt{b^2-4ac}}\right)\end{array}}$

Se define periodo en la dirección radial P_r al doble del tiempo que tarda un cuerpo celeste en desplazarse, a lo largo de la dirección radial, desde r₁ hasta r₂.

${\displaystyle \begin{array}{l}{P}_r=2{\displaystyle \underset{r_1}{\overset{r_2}{\int }}\frac{r·dr}{\sqrt{\frac{2E}{m}{r}^2+2GM·r-\frac{L^2}{m^2}}}}={\frac{2}{a}\left\{-\sqrt{-a{r}^2+br-c}+\frac{b}{2\sqrt{a}}\arcsin \left(\frac{2ar-b}{\sqrt{b^2-4ac}}\right)\right\}|}_{r_1}^{r_2}=\\ \frac{b}{a\sqrt{a}}\left\{\arcsin \left(\frac{2a{r}_2-b}{\sqrt{b^2-4ac}}\right)-\arcsin \left(\frac{2a{r}_1-b}{\sqrt{b^2-4ac}}\right)\right\}=\frac{b}{a\sqrt{a}}\left(\arcsin (1)-\arcsin (-1)\right)\end{array}}$

El periodo coincide con el calculado en la página titulada Trayectorias elípticas (I)

${\displaystyle P_r=\frac{2\pi GM}{{\left(-2\frac{E}{m}\right)}^{3/2}}}$

Periodo angular

De la constancia del momento angular deducimos la fórmula del periodo del movimiento angular.

${\displaystyle \begin{array}{l}L=m{r}^2\frac{d\theta }{dt}\\ P_{\theta }=\frac{m}{L}{\displaystyle \underset{0}{\overset{2\pi }{\int }}{r}^{2}d\theta }=\frac{m}{L}{\displaystyle \underset{0}{\overset{2\pi }{\int }}\frac{d^2}{{\left(1+\epsilon \cos \theta \right)}^2}d\theta }=2\frac{m}{L}{d}^2{\displaystyle \underset{0}{\overset{\pi }{\int }}\frac{1}{{\left(1+\epsilon \cos \theta \right)}^2}d\theta }\end{array}}$

Hacemos el cambio de variable

${\displaystyle \cos \theta =\frac{1-x^2}{1+x^2}\sin \theta =\frac{2x}{1+x^2}d\theta =\frac{2}{1+x^2}dxx=\tan \left(\frac{\theta }{2}\right)}$

La integral se convierte en

${\displaystyle {\displaystyle \int \frac{d\theta }{{\left(1+\epsilon \cos \theta \right)}^2}}=\frac{2}{{\left(1+\epsilon \right)}^2}{\displaystyle \int \frac{1+x^2}{{\left(1+a{x}^2\right)}^2}dx}a=\frac{1-\epsilon }{1+\epsilon }}$

Descomponemos el integrando, la fracción

${\displaystyle \begin{array}{l}\frac{1+x^2}{{\left(1+a{x}^2\right)}^2}=\frac{Ax+B}{{\left(1+a{x}^2\right)}^2}+\frac{Cx+D}{1+a{x}^2}\\ 1+x^2=Ax+B+\left(Cx+D\right)\left(1+a{x}^2\right),\{\begin{array}{l}A=0\\ B=\frac{a-1}{a}\end{array}\{\begin{array}{l}C=0\\ D=\frac{1}{a}\end{array}\end{array}}$

La integral se transforma en

${\displaystyle \begin{array}{l}\frac{2}{{\left(1+\epsilon \right)}^2}\left\{\frac{a-1}{a}{\displaystyle \int \frac{dx}{{\left(1+a{x}^2\right)}^2}}+\frac{1}{a}{\displaystyle \int \frac{dx}{1+a{x}^2}}\right\}=\\ \frac{2}{{\left(1+\epsilon \right)}^2}\left\{\frac{a-1}{a}\left({\displaystyle \int \frac{dx}{1+a{x}^2}}-{\displaystyle \int \frac{a{x}^2}{{\left(1+a{x}^2\right)}^2}dx}\right)+\frac{1}{a}{\displaystyle \int \frac{dx}{1+a{x}^2}}\right\}\end{array}}$

En la primera integral de la primera fila hemos sumado y restado ax², transformándose en la suma de dos integrales

La primera y tercera son inmediatas, la segunda integral se resuelve por partes

${\displaystyle \begin{array}{l}{\displaystyle \int \frac{a{x}^2}{{\left(1+a{x}^2\right)}^2}dx}\{\begin{array}{l}u=x,du=dx\\ dv=\frac{ax}{{\left(1+a{x}^2\right)}^2}dx\end{array},v=\frac{1}{2}\frac{{\left(1+a{x}^2\right)}^{-1}}{-1}=-\frac{1}{2}\frac{1}{1+a{x}^2}\\ =-\frac{1}{2}\frac{x}{1+a{x}^2}+\frac{1}{2}{\displaystyle \int \frac{1}{1+a{x}^2}dx=}-\frac{1}{2}\frac{x}{1+a{x}^2}+\frac{1}{2\sqrt{a}}{\tan }^{-1}\left(\sqrt{a}x\right)\end{array}}$

El resultado final es

${\displaystyle \begin{array}{l}\frac{2}{{\left(1+\epsilon \right)}^2}\left\{\frac{a-1}{a}\left[\frac{1}{\sqrt{a}}{\tan }^{-1}\left(\sqrt{a}x\right)+\frac{1}{2}\frac{x}{1+a{x}^2}-\frac{1}{2\sqrt{a}}{\tan }^{-1}\left(\sqrt{a}x\right)\right]+\frac{1}{a}\frac{1}{\sqrt{a}}{\tan }^{-1}\left(\sqrt{a}x\right)\right\}=\\ \frac{1}{{\left(1+\epsilon \right)}^2}\left(\frac{a+1}{a\sqrt{a}}{\tan }^{-1}\left(\sqrt{a}x\right)+\frac{a-1}{a}\frac{x}{1+a{x}^2}\right)=\end{array}}$

Deshacemos los cambios de variable y utilizamos las relaciones trigonométricas

${\displaystyle x=\tan \frac{\theta }{2}=\frac{\sin \theta }{1+\cos \theta },x^2={\tan }^2\frac{\theta }{2}=\frac{1-\cos \theta }{1+\cos \theta }}$

La expresión de la integral en términos de la variable θ es

${\displaystyle \begin{array}{l}\frac{2}{{\left(1-{\epsilon }^2\right)}^{3/2}}{\tan }^{-1}\left(\sqrt{\frac{1-\epsilon }{1+\epsilon }}\tan \frac{\theta }{2}\right)-\frac{2\epsilon }{{\left(1+\epsilon \right)}^2(1-\epsilon )}\frac{\frac{\sin \theta }{1+\cos \theta }}{1+\frac{1-\epsilon }{1+\epsilon }\frac{1-\cos \theta }{1+\cos \theta }}\\ {\displaystyle \int \frac{d\theta }{{\left(1+\epsilon \cos \theta \right)}^2}}=\frac{1}{{\left(1-{\epsilon }^2\right)}^{3/2}}\left\{2{\tan }^{-1}\left(\sqrt{\frac{1-\epsilon }{1+\epsilon }}\tan \frac{\theta }{2}\right)-\epsilon \sqrt{1-{\epsilon }^2}\frac{\sin \theta }{1+\epsilon \cos \theta }\right\}\end{array}}$

El periodo angular vale

${\displaystyle \begin{array}{l}{P}_{\theta }=2\frac{m}{L}{d}^2{\frac{1}{{\left(1-{\epsilon }^2\right)}^{3/2}}\left\{2{\tan }^{-1}\left(\sqrt{\frac{1-\epsilon }{1+\epsilon }}\tan \frac{\theta }{2}\right)-\epsilon \sqrt{1-{\epsilon }^2}\frac{\sin \theta }{1+\epsilon \cos \theta }\right\}|}_0^{\pi }=2\frac{m}{L}{d}^2\frac{1}{{\left(1-{\epsilon }^2\right)}^{3/2}}\pi \\ P_{\theta }=\frac{2\pi GM}{{\left(-2\frac{E}{m}\right)}^{3/2}}\end{array}}$

Los parámetros d y excentricidad ε está relacionados con la energía E y el momento angular L, tal como se ha deducido en la página titulada Ecuación de la trayectoria.
Obtenemos la misma expresión para P_θ que la deducida para el periodo radial P_r y la misma que la obtenida en la página titulada Trayectorias elípticas (I)

Componentes de la velocidad del cuerpo celeste

Partimos de la ecuación de la elipse en coordenadas polares y de la relación entre el parámetro d y el semieje mayor a de la elipse

${\displaystyle \begin{array}{l}r=\frac{d}{1+\epsilon \cos \theta }d=\frac{L^2}{GM{m}^2}\\ d=a(1-{\epsilon }^2)\end{array}}$

El momento angular L en coodenadas polares, se expresa

${\displaystyle \begin{array}{l}L=m{r}^2\frac{d\theta }{dt}\\ r^2\frac{d\theta }{dt}=\sqrt{GMd}\end{array}}$

La componente radial de la velocidad es

${\displaystyle \begin{array}{l}\frac{dr}{dt}=d\frac{\epsilon \sin \theta }{{\left(1+\epsilon \cos \theta \right)}^2}\frac{d\theta }{dt}=r^2\frac{\epsilon \sin \theta }{d}\frac{\sqrt{GMd}}{r^2}=\epsilon \sqrt{\frac{GM}{d}}\sin \theta \\ \frac{dr}{dt}=\epsilon \sqrt{\frac{GM}{a(1-{\epsilon }^2)}}\sin \theta \end{array}}$

Si la trayectoria es una circunferencia ε=0, la componente radial de la velocidad dr/dt es nula

La componente transversal de la velocidad es

${\displaystyle \begin{array}{l}r\frac{d\theta }{dt}=\frac{\sqrt{GMd}}{r}=\sqrt{\frac{GM}{d}}(1+\epsilon \cos \theta )\\ r\frac{d\theta }{dt}=\sqrt{\frac{GM}{a(1-{\epsilon }^2)}}(1+\epsilon \cos \theta )\end{array}}$

Si la trayectoria es una circunferencia ε=0, la componente transversal de la velocidad r·dθ/dt es constante

El vector velocidad expresado en términos del ángulo θ es

${\displaystyle \overrightarrow{v}=\left(\epsilon \sqrt{\frac{GM}{a(1-{\epsilon }^2)}}\sin \theta \right)\widehat{r}+\left(\sqrt{\frac{GM}{a(1-{\epsilon }^2)}}(1+\epsilon \cos \theta )\right)\widehat{\theta }}$

e=0.7; %excentricidad
hold on
fplot(@(x) e*sin(x),[0,pi])
fplot(@(x) 1+e*cos(x),[0,pi])
hold off
set(gca,'XTick',0:pi/4:pi)
set(gca,'XTickLabel',{'0','\pi/4','\pi/2','3\pi/4','\pi'})

grid on
ylim([0,2])
legend('v_r', 'v_{\theta}')
xlabel('\theta')
ylabel('v')
title('Componentes de la velocidad')

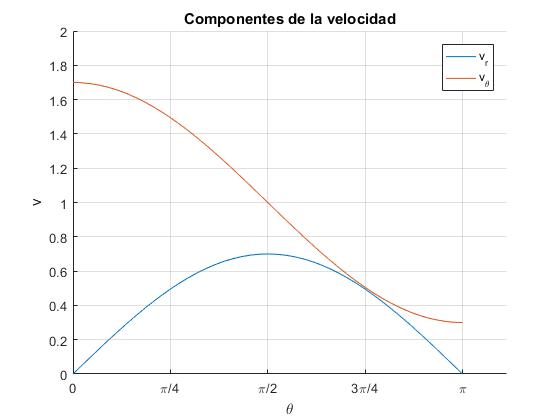
La componente radial de la velocidad dr/dt se anula en el punto más cercano y en el punto más alejado del centro de fuerzas. La componente transversal r·dθ/dt es máxima en el punto más cercano, θ=0 (perihelio o perigeo) y mínima en el más alejado, θ=π (afelio o apogeo)

${\displaystyle \begin{array}{l}{v}_p=\sqrt{\frac{GM}{a\left(1-{\epsilon }^2\right)}}(1+\epsilon )=\sqrt{\frac{GM}{a}}\sqrt{\frac{1+\epsilon }{1-\epsilon }}\\ v_a=\sqrt{\frac{GM}{a\left(1-{\epsilon }^2\right)}}(1-\epsilon )=\sqrt{\frac{GM}{a}}\sqrt{\frac{1-\epsilon }{1+\epsilon }}\end{array}}$

Para la Tierra cuya excentricidad es ε=0.0167, v_p/v_a=1.03397. Cuando la excentricidad es pequeña

${\displaystyle \frac{v_p}{v_a}=\frac{1+\epsilon }{1-\epsilon }=\frac{{\left(1+\epsilon \right)}^2}{1-{\epsilon }^2}\approx 1+2\epsilon }$

Distancia media en una trayectoria elíptica

A veces se confunde el semieje mayor de la elipse a con la distancia media entre un planeta y el Sol. En este apartado, vamos a ver que hay distintas formas de calcular la distancia media entre un planeta y el Sol y difieren del semieje mayor a de la elipse

la ecuación de la trayectoria de un cuerpo celeste alrededor del centro fijo de fuerzas, situado en el origen es

${\displaystyle r=\frac{d}{1+\epsilon \cos \theta }}$

r es la distancia del cuerpo celeste al origen y θ es la posición angular

Para θ=0, el cuerpo se encuentra a la distancia r₁ más cercana al origen y para θ=π el cuerpo celeste se encuentra más alejado r₂. Donde r₁+r₂=2a

${\displaystyle \begin{array}{l}2a=\frac{d}{1+\epsilon }+\frac{d}{1-\epsilon }\\ d=a\left(1-{\epsilon }^2\right)\\ r=\frac{a\left(1-{\epsilon }^2\right)}{1+\epsilon \cos \theta }\end{array}}$

La distancia media del cuerpo al origen no es (r₁+r₂)/2=a

Promedio angular

En la figura, se representa una elipse de semiejes a=2, b=1. El centro fijo de fuerzas está en el origen (un punto de color azul). Se señalan sobre la trayectoria, mediante puntos de color rojo, las posiciones angulares del cuerpo celeste θ=0°, 30°, 60°, 90°,... 360°

a=2; %semieje mayor
b=1; %semieje menor
e=sqrt(a^2-b^2)/a; %excentricidad
d=a*(1-e^2);
hold on
fplot(@(th) d*cos(th)./(1+e*cos(th)), @(th) d*sin(th)./(1+e*cos(th)),[0,2*pi])
plot(0,0,'bo', 'markersize',4,'markeredgecolor','b','markerfacecolor','b')
for th=(0:30:330)*pi/180 %posiciones angulares
    r=d/(1+e*cos(th));
    plot(r*cos(th),r*sin(th),'ro', 'markersize',3,'markeredgecolor',
'r','markerfacecolor','r')
end
hold off
axis equal
xlabel('x')
ylabel('y')
grid on
title('Promedio angular')

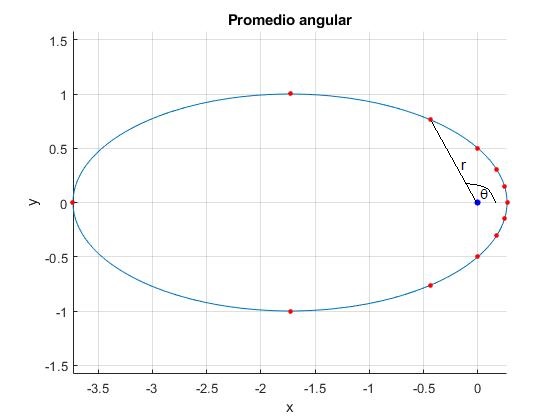
Calculamos las distancias r_n del cuerpo al origen para cada posición angular θ_n, la media es

${\displaystyle <r{>}_{\theta }\approx \frac{{\displaystyle \sum _{n=1}^N{r}_n}}{N}=\frac{a\left(1-{\epsilon }^2\right)}{N}{\displaystyle \sum _{n=1}^N\frac{1}{1+\epsilon \cos {\theta }_n}}}$

El valor exacto del promedio angular es

${\displaystyle <r{>}_{\theta }=\frac{{\displaystyle \underset{0}{\overset{2\pi }{\int }}r·d\theta }}{{\displaystyle \underset{0}{\overset{2\pi }{\int }}d\theta }}=\frac{a\left(1-{\epsilon }^2\right)}{2\pi }{\displaystyle \underset{0}{\overset{2\pi }{\int }}\frac{d\theta }{1+\epsilon \cos \theta }}=\frac{a\left(1-{\epsilon }^2\right)}{\pi }{\displaystyle \underset{0}{\overset{\pi }{\int }}\frac{d\theta }{1+\epsilon \cos \theta }}}$

Buscamos el resultado de la integral en en el libro titulado 'Table of Integrals, Series, and Products' pág. 172, 2.553, 3°

${\displaystyle {\displaystyle \int \frac{dx}{a+b\cos x}}=\frac{2}{\sqrt{a^2-b^2}}\arctan \left(\frac{(a-b)\tan \left(\frac{x}{2}\right)}{\sqrt{a^2-b^2}}\right),a^2>b^2}$

Donde a=1, b=ε con ε<1, para trayectorias elípticas

La integral definida vale

${\displaystyle {\displaystyle \underset{0}{\overset{\pi }{\int }}\frac{d\theta }{1+\epsilon \cos \theta }}={\frac{2}{\sqrt{1-{\epsilon }^2}}\arctan \left(\frac{(1-\epsilon )\tan \left(\frac{\theta }{2}\right)}{\sqrt{1-{\epsilon }^2}}\right)|}_0^{\pi }=\frac{2}{\sqrt{1-{\epsilon }^2}}\frac{\pi }{2}}$

De acuerdo con este criterio, la distancia media entre el cuerpo celeste y el centro fijo de fuerzas es

${\displaystyle <r{>}_{\theta }=\frac{a\left(1-{\epsilon }^2\right)}{\pi }\frac{\pi }{\sqrt{1-{\epsilon }^2}}=a\sqrt{1-{\epsilon }^2}}$

Esta distancia media, disminuye con la excentricidad ε. En el caso de la Tierra, su excentricidad es muy pequeña, por lo que la distancia media difiere poco del semieje mayor a

Promedio temporal

En la figura se representa una elipse de semiejes a=2, b=1. El centro fijo de fuerzas está en el origen (un punto de color azul). Se señalan sobre la trayectoria, mediante puntos de color rojo, las posiciones del cuerpo celeste en los instantes t=P/10, 2P/10, 3P/10,...P, Donde P es el periodo o tiempo que tarda el cuerpo celeste en dar una vuelta completa

${\displaystyle P=\frac{2m\pi ab}{L}=2\pi \sqrt{\frac{a^3}{GM}}}$

Para representar las posiciones del cuerpo en la trayectoria elíptica hemos supuesto que GM=1

Dado el tiempo t calculamos el ángulo E, resolviendo la ecuación transcendente

${\displaystyle E-\epsilon \sin E=2\pi \frac{t}{P}}$

Una vez calculado en ángulo E, se determina la posición angular θ

${\displaystyle \tan \left(\frac{\theta }{2}\right)=\sqrt{\frac{1+\epsilon }{1-\epsilon }}\tan \left(\frac{E}{2}\right)}$

a=2; %semieje mayor
b=1; %semieje menor
e=sqrt(a^2-b^2)/a; %excentricidad
P=2*pi*a^(3/2); %periodo
d=a*(1-e^2);
hold on
fplot(@(th) d*cos(th)./(1+e*cos(th)), @(th) d*sin(th)./(1+e*cos(th)),[0,2*pi])
plot(0,0,'bo', 'markersize',4,'markeredgecolor','b','markerfacecolor','b')
for t=P/10:P/10:P
    Me=2*pi*t/P;
    x0=Me-e/2;
    while(1)
        x=x0-(x0-e*sin(x0)-Me)/(1-e*cos(x0));
        if abs((x-x0)/x0)<1e-6
            break;
        end
        x0=x;
    end
    th=2*atan(sqrt((1+e)/(1-e))*tan(x0/2));
    r=d/(1+e*cos(th));
    plot(r*cos(th),r*sin(th),'ro', 'markersize',3,'markeredgecolor',
'r','markerfacecolor','r')
end
hold off
axis equal
xlabel('x')
ylabel('y')
grid on
title('Promedio temporal')

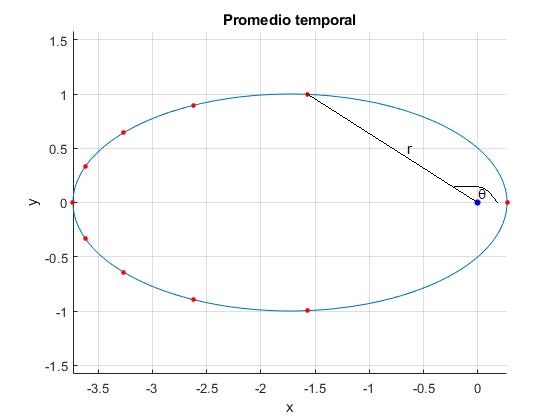
El promedio temporal es

${\displaystyle <r{>}_t=\frac{{\displaystyle \underset{0}{\overset{P}{\int }}r·dt}}{{\displaystyle \underset{0}{\overset{P}{\int }}dt}}}$

El denominador es el periodo P. Teniendo en cuenta que, el momento angular L es constante

${\displaystyle L=m{r}^2\frac{d\theta }{dt}}$

El numerador del cociente se expresa en función de la posición angular θ

${\displaystyle \begin{array}{l}{\displaystyle \underset{0}{\overset{P}{\int }}r·dt}=\frac{m}{L}{\displaystyle \underset{0}{\overset{2\pi }{\int }}{r}^3·d\theta }=\frac{P}{2\pi ab}{\displaystyle \underset{0}{\overset{2\pi }{\int }}{r}^3·d\theta }\\ <r{>}_t=\frac{a^3{\left(1-{\epsilon }^2\right)}^3}{2\pi ab}{\displaystyle \underset{0}{\overset{2\pi }{\int }}\frac{d\theta }{{\left(1+\epsilon \cos \theta \right)}^3}}=\frac{a}{\pi }{\left(1-{\epsilon }^2\right)}^{5/2}{\displaystyle \underset{0}{\overset{\pi }{\int }}\frac{d\theta }{{\left(1+\epsilon \cos \theta \right)}^3}}\end{array}}$

Buscamos el resultado de la integral en en el libro titulado 'Table of Integrals, Series, and Products' pág. 172, 2.554, 1°

${\displaystyle {\displaystyle \int \frac{A+B\cos x}{{\left(a+b\cos x\right)}^n}dx}=\frac{1}{(n-1)\left(a^2-b^2\right)}\left\{\begin{array}{l}\frac{\left(aB-bA\right)\sin x}{{\left(a+b\cos x\right)}^{n-1}}+\\ {\displaystyle \int \frac{\left(aA-bB\right)(n-1)+(n-2)\left(aB-bA\right)\cos x}{{\left(a+b\cos x\right)}^{n-1}}dx}\end{array}\right\}}$

Para el caso particular A=1, B=0, a=1, b=ε

${\displaystyle {\displaystyle \int \frac{1}{{\left(1+\epsilon \cos x\right)}^3}dx}=\frac{1}{2\left(1-{\epsilon }^2\right)}\left\{\frac{-\epsilon \sin x}{{\left(1+\epsilon \cos x\right)}^2}+{\displaystyle \int \frac{2-\epsilon \cos x}{{\left(1+\epsilon \cos x\right)}^2}dx}\right\}}$

Resolvemos ahora la integral con A=2, y B=-ε

${\displaystyle {\displaystyle \int \frac{2-\epsilon \cos x}{{\left(1+\epsilon \cos x\right)}^2}dx}=\frac{1}{\left(1-{\epsilon }^2\right)}\left\{\frac{-3\epsilon \sin x}{1+\epsilon \cos x}+\left(2+{\epsilon }^2\right){\displaystyle \int \frac{dx}{1+\epsilon \cos x}}\right\}}$

Finalmente, nos queda la integral del primer apartado, 'Promedio angular'

${\displaystyle {\displaystyle \int \frac{dx}{1+\epsilon \cos x}}=\frac{2}{\sqrt{1-{\epsilon }^2}}\arctan \left(\frac{(1-\epsilon )\tan \left(\frac{x}{2}\right)}{\sqrt{1-{\epsilon }^2}}\right)}$

Reunimos los resultados parciales

${\displaystyle {\displaystyle \int \frac{dx}{{\left(1+\epsilon \cos x\right)}^3}}=\frac{1}{2\left(1-{\epsilon }^2\right)}\left\{\frac{-\epsilon \sin x}{{\left(1+\epsilon \cos x\right)}^2}+\frac{1}{\left(1-{\epsilon }^2\right)}\left\{\frac{-3\epsilon \sin x}{1+\epsilon \cos x}+\left(2+{\epsilon }^2\right)\frac{2}{\sqrt{1-{\epsilon }^2}}\arctan \left(\frac{(1-\epsilon )\tan \left(\frac{x}{2}\right)}{\sqrt{1-{\epsilon }^2}}\right)\right\}\right\}}$

La integral definida vale

${\displaystyle {\displaystyle \underset{0}{\overset{\pi }{\int }}\frac{d\theta }{{\left(1+\epsilon \cos \theta \right)}^3}}=\frac{1}{2\left(1-{\epsilon }^2\right)}\left\{\frac{1}{\left(1-{\epsilon }^2\right)}\left\{\left(2+{\epsilon }^2\right)\frac{2}{\sqrt{1-{\epsilon }^2}}\frac{\pi }{2}\right\}\right\}=\frac{\left(2+{\epsilon }^2\right)\pi }{2{\left(1-{\epsilon }^2\right)}^{5/2}}}$

De acuerdo con este criterio, la distancia media entre el cuerpo celeste y el centro fijo de fuerzas es

${\displaystyle <r{>}_t=\frac{a}{\pi }{\left(1-{\epsilon }^2\right)}^{5/2}{\displaystyle \underset{0}{\overset{\pi }{\int }}\frac{d\theta }{{\left(1+\epsilon \cos \theta \right)}^3}}=\frac{a}{\pi }{\left(1-{\epsilon }^2\right)}^{5/2}\frac{\left(2+{\epsilon }^2\right)\pi }{2{\left(1-{\epsilon }^2\right)}^{5/2}}=a\left(1+\frac{1}{2}{\epsilon }^2\right)}$

Esta distancia media, se incrementa con la excentricidad ε. En el caso de la Tierra, su excentricidad es muy pequeña, por lo que la distancia media difiere poco del semieje mayor a

Referencias

O.L. de Lange, J. Pierrus. Solved Problems in Classical Mechanics. Analytical and numerical solutions with comments. Oxford University Press (2010). Questions 8.15, pp. 249-250

Darren M. Wiliams. Average distance between a star and a planet in a eccentric orbit. Am. J. Phys. 71 (11), November 2003, pp. 1198-1200

I.S. Gradshteyn, I.M. Ryzhik. Table of Integrals, Series, and Products, Seventh Edition, 2007 Elsevier Inc, pág. 172