Equilibrio del movimiento de rotación y traslación de un satélite alrededor de su planeta

Estudiamos un sistema aislado formado por dos cuerpos celestes de masas m₁ y m₂ que se mueven bajo su fuerza de interacción mutua, alrededor del centro de masas, c. m. en reposo. Además los cuerpos giran alrededor de sus ejes (perpendiculares al plano de las órbitas) con velocidad angular ω₁ y ω₂, respectivamente.

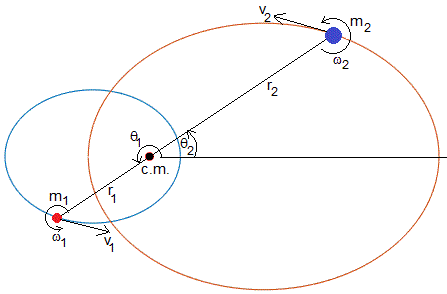
Las órbitas de los dos cuerpos celestes se representan mediante el código

m2=1; %masas
m1=2*m2;
e=0.65; %excentricidad

%trayectorias en el sistema CM
th=1:360;
radio=1./(1+e*cos(th*pi/180));
x1=radio.*cos(th*pi/180)*m2/(m1+m2);
y1=radio.*sin(th*pi/180)*m2/(m1+m2);
x2=-radio.*cos(th*pi/180)*m1/(m1+m2);
y2=-radio.*sin(th*pi/180)*m1/(m1+m2);
hold on
plot(x1,y1)
plot(x2,y2)
plot(0,0,'o','markersize',6, 'markeredgecolor','r','markerfacecolor','r')
hold off
axis equal
axis off

Tomando el centro de masa como origen se cumple que

$m_{1} r_{1} = m_{2} r_{2}$

El centro de masa está en reposo

$m_{1} \vec{v_{1}} + m_{2} \vec{v_{2}} = 0$

Expresamos la velocidad en coordenadas polares

$\vec{v} = \frac{d r}{d t} \hat{r} + r \frac{d θ}{d t} \hat{θ}$

Se cumple que

${\begin{cases} m_{1} \frac{d r_{1}}{d t} + m_{2} \frac{d r_{2}}{d t} = 0 \\ m_{1} r_{1} \frac{d θ_{1}}{d t} + m_{2} r_{2} \frac{d θ_{2}}{d t} = 0 \end{cases}$

Por ser un sistema aislado, el momento angular total permanece constante

$\begin{array}{l} L = m_{1} r_{1} (r_{1} \frac{d θ_{1}}{d t}) + m_{2} r_{2} (r_{2} \frac{d θ_{2}}{d t}) + I_{1} ω_{1} + I_{2} ω_{2} \\ L = m_{1} r_{1}^{2} \frac{d θ_{1}}{d t} + m_{2} r_{2}^{2} \frac{d θ_{2}}{d t} + I_{1} ω_{1} + I_{2} ω_{2} \end{array}$

y la energía permanece constante

$E = \frac{1}{2} m_{1} ({(\frac{d r_{1}}{d t})}^{2} + r_{1}^{2} {(\frac{d θ_{1}}{d t})}^{2}) + \frac{1}{2} m_{2} ({(\frac{d r_{2}}{d t})}^{2} + r_{2}^{2} {(\frac{d θ_{2}}{d t})}^{2}) - G \frac{m_{1} m_{2}}{r_{1} + r_{2}} + \frac{1}{2} I_{1} ω_{1}^{2} + \frac{1}{2} I_{2} ω_{2}^{2}$

De las ecuaciones

$\begin{array}{l} {\begin{cases} m_{1} r_{1} = m_{2} r_{2} \\ m_{1} r_{1} \frac{d θ_{1}}{d t} + m_{2} r_{2} \frac{d θ_{2}}{d t} = 0 \end{cases} \\ \frac{d θ_{1}}{d t} = \frac{d θ_{2}}{d t} = \frac{d θ}{d t} \end{array}$

La velocidad angular de traslación de la dos partículas es la misma, dθ/dt

Despejamos la velocidad angular de traslación, dθ/dt del momento angular

$\begin{array}{l} L = (m_{1} r_{1}^{2} + m_{2} r_{2}^{2}) \frac{d θ}{d t} + I_{1} ω_{1} + I_{2} ω_{2} \\ \frac{d θ}{d t} = \frac{L - I_{1} ω_{1} - I_{2} ω_{2}}{m_{1} {(\frac{m_{2} r_{2}}{m_{1}})}^{2} + m_{2} r_{2}^{2}} \\ \frac{d θ}{d t} = \frac{m_{1} (L - I_{1} ω_{1} - I_{2} ω_{2})}{m_{2} r_{2}^{2} (m_{1} + m_{2})} \end{array}$

Energía potencial efectiva

Expresamos la energía potencial efectiva en función de tres variables: posición de la segunda partícula r₂, velocidades angulares de rotación ω₁ y ω₂

$\begin{array}{l} V_{e} = \frac{1}{2} (m_{1} r_{1}^{2} + m_{2} r_{2}^{2}) {(\frac{d θ}{d t})}^{2} - G \frac{m_{1} m_{2}}{{(r_{1} + r_{2})}^{2}} + \frac{1}{2} I_{1} ω_{1}^{2} + \frac{1}{2} I_{2} ω_{2}^{2} \\ V_{e} = \frac{1}{2} (m_{1} {(\frac{m_{2} r_{2}}{m_{1}})}^{2} + m_{2} r_{2}^{2}) {(\frac{m_{1} (L - I_{1} ω_{1} - I_{2} ω_{2})}{m_{2} r_{2}^{2} (m_{1} + m_{2})})}^{2} - G \frac{m_{1} m_{2}}{(\frac{m_{2} r_{2}}{m_{1}}) + r_{2}} + \frac{1}{2} I_{1} ω_{1}^{2} + \frac{1}{2} I_{2} ω_{2}^{2} \\ V_{e} = \frac{1}{2} \frac{m_{1} {(L - I_{1} ω_{1} - I_{2} ω_{2})}^{2}}{m_{2} r_{2}^{2} (m_{1} + m_{2})} - G \frac{m_{1}^{2} m_{2}}{(m_{1} + m_{2}) r_{2}} + \frac{1}{2} I_{1} ω_{1}^{2} + \frac{1}{2} I_{2} ω_{2}^{2} \\ V_{e} = \frac{1}{2} m_{1} \frac{(L^{2} + I_{1}^{2} ω_{1}^{2} + I_{2}^{2} ω_{2}^{2} - 2 L I_{1} ω_{1} - 2 L I_{2} ω_{2} + 2 I_{1} ω_{1} I_{2} ω_{2})}{m_{2} r_{2}^{2} (m_{1} + m_{2})} - G \frac{m_{1}^{2} m_{2}}{(m_{1} + m_{2}) r_{2}} + \frac{1}{2} I_{1} ω_{1}^{2} + \frac{1}{2} I_{2} ω_{2}^{2} \end{array}$

Demostraremos que el mínimo de de la energía potencial efectiva V_e corresponde a la situación

$\frac{d θ}{d t} = ω_{1} = ω_{2}$

Es conveniente expresar la energía potencial efectiva en términos de magnitudes adimensionales

$\begin{array}{l} R_{2} = \frac{G m_{1} m_{2}^{2}}{L^{2}} r_{2}, Ω_{1} = \frac{L^{3} (m_{1} + m_{2})}{G^{2} m_{1}^{3} m_{2}^{3}} ω_{1}, Ω_{2} = \frac{L^{3} (m_{1} + m_{2})}{G^{2} m_{1}^{3} m_{2}^{3}} ω_{2} \\ k_{1} = \frac{G^{2} m_{1}^{3} m_{2}^{3}}{L^{4} (m_{1} + m_{2})} I_{1}, k_{2} = \frac{G^{2} m_{1}^{3} m_{2}^{3}}{L^{4} (m_{1} + m_{2})} I_{2} \end{array}$

Teniendo en cuenta que

$\begin{array}{l} I_{1} ω_{1} = \frac{L^{4} (m_{1} + m_{2})}{G^{2} m_{1}^{3} m_{2}^{3}} k_{1} \frac{G^{2} m_{1}^{3} m_{2}^{3}}{L^{3} (m_{1} + m_{2})} Ω_{1} = L \cdot k_{1} Ω_{1} \\ I_{1} ω_{1}^{2} = \frac{L^{4} (m_{1} + m_{2})}{G^{2} m_{1}^{3} m_{2}^{3}} k_{1} {(\frac{G^{2} m_{1}^{3} m_{2}^{3}}{L^{3} (m_{1} + m_{2})} Ω_{1})}^{2} = \frac{G^{2} m_{1}^{3} m_{2}^{3}}{L^{2} (m_{1} + m_{2})} k_{1} Ω_{1}^{2} \end{array}$

Lo mismo con I₂ y ω₂

$\begin{array}{l} V_{e} = \frac{1}{2} \frac{m_{1} L^{2}}{m_{2} {(\frac{L^{2}}{G m_{1} m_{2}^{2}})}^{2} R_{2}^{2} (m_{1} + m_{2})} + \frac{1}{2} \frac{m_{1} L^{2} k_{1}^{2} Ω_{1}^{2}}{m_{2} {(\frac{L^{2}}{G m_{1} m_{2}^{2}})}^{2} R_{2}^{2} (m_{1} + m_{2})} + \frac{1}{2} \frac{m_{1} L^{2} k_{2}^{2} Ω_{2}^{2}}{m_{2} {(\frac{L^{2}}{G m_{1} m_{2}^{2}})}^{2} R_{2}^{2} (m_{1} + m_{2})} \\ - \frac{m_{1} L^{2} k_{1} Ω_{1}}{m_{2} {(\frac{L^{2}}{G m_{1} m_{2}^{2}})}^{2} R_{2}^{2} (m_{1} + m_{2})} - \frac{m_{1} L^{2} k_{2} Ω_{2}}{m_{2} {(\frac{L^{2}}{G m_{1} m_{2}^{2}})}^{2} R_{2}^{2} (m_{1} + m_{2})} + \frac{m_{1} L^{2} k_{1} k_{2} Ω_{1} Ω_{2}}{m_{2} {(\frac{L^{2}}{G m_{1} m_{2}^{2}})}^{2} R_{2}^{2} (m_{1} + m_{2})} \\ - G \frac{m_{1}^{2} m_{2}}{(m_{1} + m_{2}) (\frac{L^{2}}{G m_{1} m_{2}^{2}}) R_{2}} + \frac{1}{2} \frac{G^{2} m_{1}^{3} m_{2}^{3}}{L^{2} (m_{1} + m_{2})} k_{1} Ω_{1}^{2} + \frac{1}{2} \frac{G^{2} m_{1}^{3} m_{2}^{3}}{L^{2} (m_{1} + m_{2})} k_{2} Ω_{2}^{2} \end{array}$

Después de simplificar y agrupar términos, el resultado final es

$V_{e} = \frac{1}{2} \frac{G^{2} m_{1}^{3} m_{2}^{3}}{(m_{1} + m_{2}) L^{2}} {\frac{1}{R_{2}^{2}} + {(\frac{k_{1} Ω_{1} + k_{2} Ω_{2}}{R_{2}})}^{2} - \frac{2}{R_{2}} - \frac{2 k_{1} Ω_{1}}{R_{2}^{2}} - \frac{2 k_{2} Ω_{2}}{R_{2}^{2}} + k_{1} Ω_{1}^{2} + k_{2} Ω_{2}^{2}}$

Mínimo de la energía potencial efectiva

El extremo de la función V_e(R₂, Ω₁, Ω₁) se calcula

$\frac{\partial V_{e}}{\partial R_{2}} = \frac{\partial V_{e}}{\partial Ω_{2}} = \frac{\partial V_{e}}{\partial Ω_{1}} = 0$

Derivamos respecto de Ω₁

$\begin{array}{l} \frac{\partial}{\partial Ω_{1}} {\frac{1}{R_{2}^{2}} + {(\frac{k_{1} Ω_{1} + k_{2} Ω_{2}}{R_{2}})}^{2} - \frac{2}{R_{2}} - \frac{2 k_{1} Ω_{1}}{R_{2}^{2}} - \frac{2 k_{2} Ω_{2}}{R_{2}^{2}} + k_{1} Ω_{1}^{2} + k_{2} Ω_{2}^{2}} = 0 \\ 2 k_{1} \frac{k_{1} Ω_{1} + k_{2} Ω_{2}}{R_{2}^{2}} - \frac{2 k_{1}}{R_{2}^{2}} + 2 k_{1} Ω_{1} = 0 \\ (k_{1} + R_{2}^{2}) Ω_{1} + k_{2} Ω_{2} = 1 \end{array}$

Derivamos respecto de Ω₂

$\begin{array}{l} \frac{\partial}{\partial Ω_{2}} {\frac{1}{R_{2}^{2}} + {(\frac{k_{1} Ω_{1} + k_{2} Ω_{2}}{R_{2}})}^{2} - \frac{2}{R_{2}} - \frac{2 k_{1} Ω_{1}}{R_{2}^{2}} - \frac{2 k_{2} Ω_{2}}{R_{2}^{2}} + k_{1} Ω_{1}^{2} + k_{2} Ω_{2}^{2}} = 0 \\ 2 k_{2} \frac{k_{1} Ω_{1} + k_{2} Ω_{2}}{R_{2}^{2}} - \frac{2 k_{2}}{R_{2}^{2}} + 2 k_{2} Ω_{2} = 0 \\ k_{1} Ω_{1} + (k_{2} + R_{2}^{2}) Ω_{2} = 1 \end{array}$

Resolvemos el sistema de dos ecuaciones

$\begin{array}{l} {\begin{cases} (k_{1} + R_{2}^{2}) Ω_{1} + k_{2} Ω_{2} = 1 \\ k_{1} Ω_{1} + (k_{2} + R_{2}^{2}) Ω_{2} = 1 \end{cases} \\ Ω_{1} = Ω_{2} = \frac{1}{k_{1} + k_{2} + R_{2}^{2}} \end{array}$

Hemos demostrado que en el mínimo se cumple que Ω₁=Ω₂ y por tanto, ω₁=ω₂. Las velocidades angulares de rotación del planeta y del satélite alrededor de sus ejes respectivos son iguales

Nos falta demostrar que la velocidad angular del centro del satélite cuando se mueve alrededor del planeta, dθ/dt=ω₁. Partimos de la expresión

$\frac{d θ}{d t} = \frac{m_{1} (L - I_{1} ω_{1} - I_{2} ω_{2})}{m_{2} r_{2}^{2} (m_{1} + m_{2})}$

Expresada en términos de unidades adimensionales

$\frac{d θ}{d t} = \frac{m_{1} (L - L \cdot k_{1} Ω_{1} - L \cdot k_{2} Ω_{2})}{m_{2} {(\frac{L^{2}}{G m_{1} m_{2}^{2}})}^{2} R_{2}^{2} (m_{1} + m_{2})} = \frac{G^{2} m_{1}^{3} m_{2}^{3}}{L^{3} (m_{1} + m_{2}) R_{2}^{2}} (1 - k_{1} Ω_{1} - k_{2} Ω_{1})$

En el mínimo

$R_{2}^{2} Ω_{1} = 1 - k_{1} Ω_{1} - k_{2} Ω_{1}$

El resultado es

$\frac{d θ}{d t} = \frac{G^{2} m_{1}^{3} m_{2}^{3}}{L^{3} (m_{1} + m_{2}) R_{2}^{2}} R_{2}^{2} Ω_{1} = \frac{G^{2} m_{1}^{3} m_{2}^{3}}{L^{3} (m_{1} + m_{2})} Ω_{1} = ω_{1}$

Derivamos respecto de R₂

$\begin{array}{l} \frac{\partial}{\partial R_{2}} {\frac{1}{R_{2}^{2}} + {(\frac{k_{1} Ω_{1} + k_{2} Ω_{2}}{R_{2}})}^{2} - \frac{2}{R_{2}} - \frac{2 k_{1} Ω_{1}}{R_{2}^{2}} - \frac{2 k_{2} Ω_{2}}{R_{2}^{2}} + k_{1} Ω_{1}^{2} + k_{2} Ω_{2}^{2}} = 0 \\ - \frac{2}{R_{2}^{3}} - \frac{2 {(k_{1} Ω_{1} + k_{2} Ω_{2})}^{2}}{R_{2}^{3}} + \frac{2}{R_{2}^{2}} + \frac{4 k_{1} Ω_{1}}{R_{2}^{3}} + \frac{4 k_{2} Ω_{2}}{R_{2}^{3}} = 0 \\ - 1 - {(k_{1} + k_{2})}^{2} Ω_{1}^{2} + R_{2} + 2 (k_{1} + k_{2}) Ω_{1} = 0 \\ - 1 - {(\frac{k_{1} + k_{2}}{k_{1} + k_{2} + R_{2}^{2}})}^{2} + R_{2} + \frac{2 (k_{1} + k_{2})}{k_{1} + k_{2} + R_{2}^{2}} = 0 \\ - {(k_{1} + k_{2} + R_{2}^{2})}^{2} - {(k_{1} + k_{2})}^{2} + R_{2} {(k_{1} + k_{2} + R_{2}^{2})}^{2} + 2 (k_{1} + k_{2}) (k_{1} + k_{2} + R_{2}^{2}) = 0 \\ {(k_{1} + k_{2} + R_{2}^{2})}^{2} - R_{2}^{3} = 0 \\ R_{2}^{4} - R_{2}^{3} + 2 (k_{1} + k_{2}) R_{2}^{2} + 2 k_{1} k_{2} = 0 \end{array}$

Esta ecuación tiene dos raíces reales y otras dos complejas congugadas si

$k_{1} + k_{2} \leq \frac{27}{256}$

de otro modo, las cuatro raíces son complejas y el potencial efectivo no tiene mínimo local. Esta condición es equivalente a

$\begin{array}{l} \frac{G^{2} m_{1}^{3} m_{2}^{3}}{L^{4} (m_{1} + m_{2})} I_{1} + \frac{G^{2} m_{1}^{3} m_{2}^{3}}{L^{4} (m_{1} + m_{2})} I_{2} \leq \frac{3^{3}}{4^{4}} \\ L^{4} \geq \frac{3 \cdot 4^{4}}{3^{4}} \frac{G^{2} m_{1}^{3} m_{2}^{3}}{m_{1} + m_{2}} (I_{1} + I_{2}) \\ L \geq \frac{4}{3} {(\frac{3 G^{2} m_{1}^{3} m_{2}^{3}}{m_{1} + m_{2}} (I_{1} + I_{2}))}^{1 / 4} \end{array}$

El satélite es una partícula

El segundo objeto celeste es una masa puntual, de modo que el momento de inercia I₂=0, y la velocidad angular de rotación ω₂ no existe. Llamamos I=I₁, ω=ω₁ M=m₁ y m=m₂

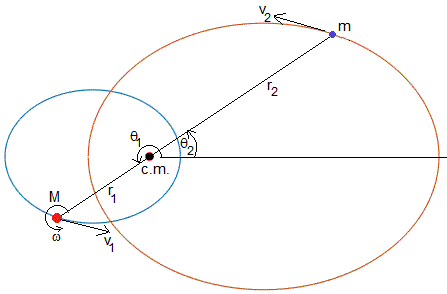
El momento angular y la energía potencial efectiva para este sistema son

$\begin{array}{l} L = (M r_{1}^{2} + m r_{2}^{2}) \frac{d θ}{d t} + I ω \\ V_{e} = \frac{1}{2} (M r_{1}^{2} + m r_{2}^{2}) {(\frac{d θ}{d t})}^{2} - G \frac{M m}{{(r_{1} + r_{2})}^{2}} + \frac{1}{2} I ω^{2} \end{array}$

Expresamos la energía potencial efectiva en función de dos variables ω y r₂

$V_{e} = \frac{1}{2} \frac{M {(L - I ω)}^{2}}{m r_{2}^{2} (M + m)} - G \frac{M^{2} m}{(M + m) r_{2}} + \frac{1}{2} I ω^{2}$

Es conveniente expresar la energía potencial efectiva en términos de magnitudes adimensionales

$\begin{array}{l} R_{2} = \frac{G M m^{2}}{L^{2}} r_{2}, Ω = \frac{L^{3} (m + M)}{G^{2} M^{3} m^{3}} ω \\ k = \frac{G^{2} M^{3} m^{3}}{L^{4} (m + M)} I \\ V_{e} = \frac{1}{2} \frac{G^{2} M^{3} m^{3}}{(m + M) L^{2}} {\frac{1}{R_{2}^{2}} + \frac{k^{2} Ω^{2}}{R_{2}^{2}} - \frac{2}{R_{2}} - \frac{2 k Ω}{R_{2}^{2}} + k Ω^{2}} \end{array}$

Mínimo de la energía potencial efectiva

El extremo de la función V_e(R₂, Ω) se calcula

$\frac{\partial V_{e}}{\partial Ω} = \frac{\partial V_{e}}{\partial R_{2}} = 0$

Derivamos respecto de Ω

$\begin{array}{l} \frac{\partial V_{e}}{\partial Ω} = \frac{\partial}{\partial Ω} {\frac{1}{R_{2}^{2}} + \frac{k^{2} Ω^{2}}{R_{2}^{2}} - \frac{2}{R_{2}} - \frac{2 k Ω}{R_{2}^{2}} + k Ω^{2}} = 0 \\ 2 \frac{k^{2} Ω}{R_{2}^{2}} - \frac{2 k}{R_{2}^{2}} + 2 k Ω = 0 \\ Ω = \frac{1}{k + R_{2}^{2}} \end{array}$

Derivamos respecto de R₂

$\begin{array}{l} \frac{\partial V_{e}}{\partial R_{2}} = - \frac{2}{R_{2}^{3}} - 2 \frac{k^{2} Ω^{2}}{R_{2}^{3}} + \frac{2}{R_{2}^{2}} + \frac{4 k Ω}{R_{2}^{3}} = 0 \\ - 1 - {(\frac{k}{k + R_{2}^{2}})}^{2} + R_{2} + \frac{2 k}{k + R_{2}^{2}} = 0 \\ R_{2}^{4} - R_{2}^{3} + 2 k R_{2}^{2} + k^{2} = 0 \end{array}$

Orbitas circulares con M>>m

Cuando la masa del planeta M es mucho mayor que la del satélite m, el centro del planeta es el c.m. del sistema y se convierte en un centro fijo de fuerzas, r₂=r es la distancia del planeta al satélite

De la dinámica del movimiento circular uniforme

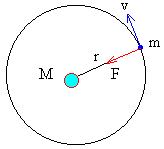
$\begin{array}{l} m \frac{v^{2}}{r} = G \frac{M m}{r^{2}} \\ {(r \frac{d θ}{d t})}^{2} = G \frac{M}{r} \\ {(\frac{d θ}{d t})}^{2} = G \frac{M}{r^{3}} \end{array}$

El momento angular es

$\begin{array}{l} L = m v r + I ω \\ L = m \sqrt{G M r} + I ω \end{array}$

Cuando lo expresamos en términos de magnitudes adimensionales, tenemos en cuenta que si m<<M entonces m+M≈M, obtenemos la velocidad angular de rotación Ω del planeta

$\begin{array}{l} R = \frac{G M m^{2}}{L^{2}} r, Ω = \frac{L^{3}}{G^{2} M^{2} m^{3}} ω \\ k = \frac{G^{2} M^{2} m^{3}}{L^{4}} I \\ L = m \sqrt{G M \frac{L^{2}}{G M m^{2}} R} + \frac{L^{4}}{G^{2} M^{2} m^{3}} k \frac{G^{2} M^{2} m^{3}}{L^{3}} Ω \\ 1 = \sqrt{R} + k Ω \\ Ω = \frac{1 - \sqrt{R}}{k} \end{array}$

En el apartado anterior, obtuvimos otra expresión para Ω

$\begin{array}{l} Ω = \frac{1}{k + R^{2}} \\ \frac{1 - \sqrt{R}}{k} = \frac{1}{k + R^{2}} \\ \frac{R^{2}}{k + R^{2}} = \sqrt{R} \\ R^{3} = {(k + R^{2})}^{2} \\ R^{4} - R^{3} + 2 k R^{2} + k^{2} = 0 \end{array}$

Expresión que obtendremos más abajo, cuando la derivada de V_e respecto de R se hace cero (extremo de la función).

Comprobamos que la velocidad angular dθ/dt del satélite (masa puntual) alrededor del planeta, es igual a la velocidad angular de rotación del planeta ω alrededor de su eje

$\begin{array}{l} \frac{d θ}{d t} = \sqrt{\frac{G M}{r^{3}}} = \sqrt{\frac{G M}{{(\frac{L^{2}}{G M m^{2}} R)}^{3}}} = \frac{G^{2} M^{2} m^{3}}{L^{3}} \sqrt{\frac{1}{R^{3}}} = \frac{G^{2} M^{2} m^{3}}{L^{3}} \sqrt{\frac{1}{{(k + R^{2})}^{2}}} \\ \frac{d θ}{d t} = \frac{G^{2} M^{2} m^{3}}{L^{3}} \frac{1}{k + R^{2}} = \frac{G^{2} M^{2} m^{3}}{L^{3}} Ω = ω \end{array}$

Sustituimos Ω en la energía potencial efectiva, teniendo en cuenta m<<M

$\begin{array}{l} V_{e} = \frac{G^{2} M^{2} m^{3}}{2 L^{2}} {\frac{1}{R^{2}} + \frac{k^{2} Ω^{2}}{R^{2}} - \frac{2 k Ω}{R^{2}} - \frac{2}{R} + k Ω^{2}} \\ V_{e} = \frac{G^{2} M^{2} m^{3}}{2 L^{2}} {\frac{1}{R^{2}} + \frac{k^{2} {(\frac{1 - \sqrt{R}}{k})}^{2}}{R^{2}} - \frac{2 k (\frac{1 - \sqrt{R}}{k})}{R^{2}} - \frac{2}{R} + k {(\frac{1 - \sqrt{R}}{k})}^{2}} \\ V_{e} = \frac{G^{2} M^{2} m^{3}}{2 L^{2}} {\frac{1}{k} {(1 - \sqrt{R})}^{2} - \frac{1}{R}} \end{array}$

Representamos la energía potencial efectiva para tres valores de k=0.05, 27/256 y 2.

hold on
k=0.05;
f=@(x) (1-sqrt(x)).^2/k-1./x;
fplot(f,[0,1.5])
line([0.8831,0.8831],[-2,f(0.8831)],'lineStyle','--')
line([0.2021,0.2021],[-2,f(0.2021)],'lineStyle','--')
k=27/256;
f=@(x) (1-sqrt(x)).^2/k-1./x;
fplot(f,[0,1.5])
line([0.5625,0.5625],[-2,f(0.5625)])
k=2;
f=@(x) (1-sqrt(x)).^2/k-1./x;
fplot(f,[0,1.5])
hold off
grid on
ylim([-2,2])
xlabel('R')
ylabel('V_e')
title('Energía potencial efectiva')

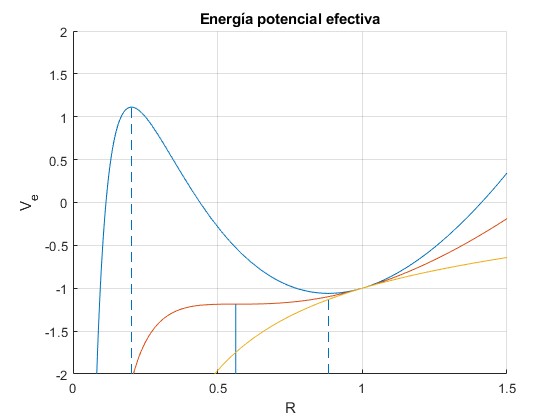
Para R=1, V_e es independiente de k y es proporcional a -1. Por esa razón, todas las curvas pasan por el punto (1,-1)

Para k<27/256, la función tiene un máximo y mínimo local. Para k>27/256 el máximo y mínimo desaparecen, no existe equilibrio. La línea de separación entre estas dos situaciones corresponde a k=27/256.

>> k=0.05;
>> roots([1,-1,2*k,0,k^2])
ans =
   0.8831 + 0.0000i
   0.2021 + 0.0000i
  -0.0426 + 0.1104i
  -0.0426 - 0.1104i
>> k=27/256;
>> roots([1,-1,2*k,0,k^2])
ans =
   0.5625 + 0.0000i
   0.5625 - 0.0000i
  -0.0625 + 0.1768i
  -0.0625 - 0.1768i
>> k=2;
>> roots([1,-1,2*k,0,k^2])
ans =
   0.7319 + 1.7371i
   0.7319 - 1.7371i
  -0.2319 + 1.0354i
  -0.2319 - 1.0354i

Para k=0.05, hay dos raíces reales, el máximo de V_e se produce para R=0.2021 y el mínimo para R=0.8831. Para k=27/256, se obtiene un punto de inflexión R=0.5625, que es una raíz doble, y para k>27/256, las cuatro raíces son complejas

Los extremos se producen

$\begin{array}{l} \frac{\partial V_{e}}{\partial R} = \frac{\partial V_{e}}{\partial R} {\frac{1}{k} {(1 - \sqrt{R})}^{2} - \frac{1}{R}} = 0 \\ \frac{1}{k} (1 - \frac{1}{\sqrt{R}}) + \frac{1}{R^{2}} = 0 \\ 1 + \frac{k}{R^{2}} = \frac{1}{\sqrt{R}} \\ {(1 + \frac{k}{R^{2}})}^{2} = \frac{1}{R} \\ R^{4} - R^{3} + 2 k R^{2} + k^{2} = 0 \end{array}$

La ecuación de cuarto grado

$x^{4} + 2 a x^{3} + b x^{2} + 2 c x + d = 0, {\begin{cases} a = - \frac{1}{2} \\ b = 2 k \\ c = 0 \\ d = k^{2} \end{cases}$

Se reduce a una ecuación de tercer grado

$\begin{array}{l} z^{3} - \frac{b}{2} z^{2} + (c a - d) z + \frac{b d - a^{2} d - c^{2}}{2} = 0 \\ z^{3} - k z^{2} - k^{2} z + k^{3} - \frac{1}{8} k^{2} = 0 \end{array}$

La ecuación cúbica tiene tres raíces reales si

$\begin{array}{l} z^{3} + a z^{2} + b z + c = 0, {\begin{cases} a = - k \\ b = - k^{2} \\ c = k^{3} - \frac{1}{8} k^{2} \end{cases} \\ Q = \frac{a^{2} - 3 b}{9}, R = \frac{2 a^{3} - 9 a b + 27 c}{54} \\ R^{2} < Q^{3} \end{array}$

En caso contrario, la ecuación cúbica tiene una raíz real y dos complejas conjugadas

Utilizamos Math Symbolic de MATLAB para calcular la diferencia R²-Q³

>> syms k;
>> a=-k;
>> b=-k^2;
>> c=k^3-k^2/8;
>> Q=(a^2-3*b)/9;
>> R=(2*a^3-9*a*b+27*c)/54;
>> z=R^2-Q^3;
>> simplify(z)
ans =-(k^4*(256*k - 27))/6912

El resultado es

$- \frac{k^{4} (256 k - 27))}{6912}$

Se cumple la desigualdad R²-Q³<0 si 256k-27>0, es decir, si $k > \frac{27}{256}$ . Por ejemplo, k=2, las raíces del polinomio de cuarto grado son todas complejas, si k=0.05<27/256 dos raíces son reales

Finalmente, comprobamos que las dos fórmulas de Ω producen los mismos resultados en el máximo y en el mínimo

$Ω = \frac{1 - \sqrt{R}}{k}, Ω = \frac{1}{k + R^{2}}$

>> k=0.05;
>> R=0.8831;
>> (1-sqrt(R))/k
ans =    1.2053
>> 1/(k+R^2)
ans =    1.2050
>> R=0.2021;
>> (1-sqrt(R))/k
ans =   11.0089
>> 1/(k+R^2)
ans =   11.0078

El caso de Fobos

Fobos es un satélite muy pequeño que gira alrededor de Marte. Los datos del sistema de dos cuerpos celestes son

masa de Marte, M=6.39·10²³ kg
momento de inercia de Marte, I=2.96·10³⁶kgm²
velocidad angular de rotación de Marte en torno a su eje, ω=7.09·10^-5 rad/s
masa de Fobos, m=1.08·10¹⁶ kg
radio de la órbita circular de Fobos, r=9.37·10⁶ m

Velocidad angular dθ/dt de Fobos alrededor de Marte

$\frac{d θ}{d t} = \sqrt{\frac{G M}{r^{3}}}$

Momento angular L constante

$L = m r^{2} (\frac{d θ}{d t}) + I ω$

El radio R (adimensional) inicial de Fobos es

$R = \frac{G M m^{2}}{L^{2}} r$

Parámetro k

$k = \frac{G^{2} M^{2} m^{3}}{L^{4}} I$

Resolvemos la ecuación de cuarto grado

$R^{4} - R^{3} + 2 k R^{2} + k^{2} = 0$

M=6.39e23; %masa de Marte
I=2.96e36; %momento de inercia de Marte
w=7.09e-5; %velocidad angular de rotación de Marte
m=1.08e16; %masa de Fobos
r=9.37e6; %radio de la órbita de Fobos
G=6.67e-11; %constante de la gravitación universal

%velocidad angular de traslación de Fobos
w_f=sqrt(G*M/r^3);
L=m*r^2*w_f^2+I*w; %momento angular
R=G*M*m^2*r/L^2; %radio inicial de Fobos
k=G^2*M^2*m^3*I/L^4; %parámetro k
raices=roots([1,-1,2*k,0,k^2]);

R =   1.0576e-12
>> format long
>> raices
raices =
  1.000000000000000 + 0.000000000000000i
 -0.000000000001151 + 0.000000000001993i
 -0.000000000001151 - 0.000000000001993i
  0.000000000002302 + 0.000000000000000i

El radio adimensional inicial de Fobos es R=1.0576·10^-12

Al resolver la ecuación de cuarto grado, obtenemos dos raices reales R=1 y R=2.302·10^-12

El radio inicial R=1.0576·10^-12 de Fobos es menor que el radio del máximo 2.302·10^-12, al disminuir la energía del sistema Marte-Fobos debida a las fuerzas de marea, el destino final de Fobos será la superficie de Marte

Representamos la energía potencial efectiva V_e en el intervalo R=(0.5·10^-12, 3.5·10^-12). Observamos el máximo y a la izquierda la posición inicial de Fobos.

Añadimos al script anterior las siguientes líneas de código

...
    hold on
f=@(x) (1-sqrt(x)).^2/k-1./x;
fplot(f,[0.5e-12,3.5e-12])
line([2.302e-12,2.302e-12],[f(0.5e-12),f(2.302e-12)])
line([R,R],[f(0.5e-12),f(R)])
plot(R,f(R),'ro','markersize',3,'markerfacecolor','r')
hold off
grid on
xlabel('R')
ylabel('V_e')
title('Energía potencial efectiva')

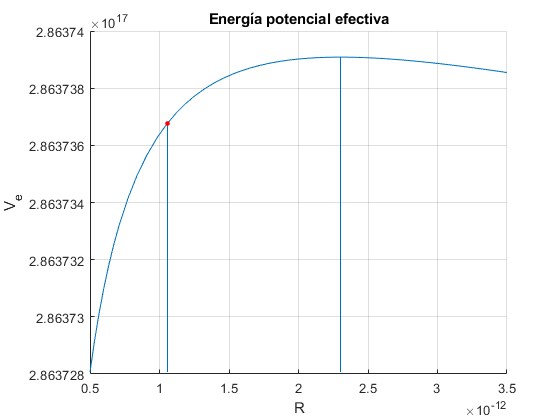
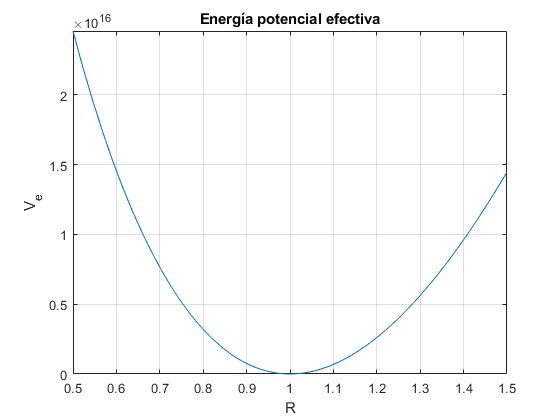
Representamos la energía potencial efectiva V_e alrededor de su mínimo R=1 que es inalcanzable por Fobos

M=6.39e23; %masa de Marte
I=2.96e36; %momento de inercia de Marte
w=7.09e-5; %velocidad angular de rotación de Marte
m=1.08e16; %masa de Fobos
r=9.37e6; %radio de la órbita de Fobos
G=6.67e-11; %constante de la gravitación universal

%velocidad angular de traslación de Fobos
w_f=sqrt(G*M/r^3);
L=m*r^2*w_f^2+I*w; %momento angular
k=G^2*M^2*m^3*I/L^4; %parámetro k

f=@(x) (1-sqrt(x)).^2/k-1./x;
fplot(f,[0.5,1.5])
grid on
xlabel('R')
ylabel('V_e')
title('Energía potencial efectiva')

Referencias

Andrea Ferroglia, Miguel C. N. Fiolhais. Tidal locking and the gravitational fold catastrophe. Am. J. Phys. 88 (12), December 2020. pp. 1059-1067