Supernova en un sistema binario

Consideremos un sistema aislado formado por dos cuerpos: un cuerpo de masa m₁ y otro cuerpo de masa m₂ bajo la acción de la fuerza de atracción mutua.

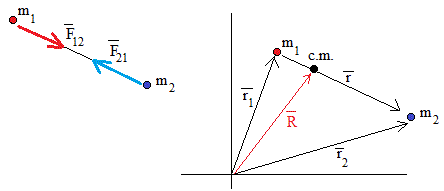
La segunda ley de Newton para cada uno de los cuerpos se escribe

$m_{1} \frac{d^{2} \vec{r_{1}}}{d t^{2}} = \vec{F_{12}} m_{2} \frac{d^{2} \vec{r_{2}}}{d t^{2}} = \vec{F_{21}}$

Por la tercera ley de Newton, la fuerza con que atrae el cuerpo 1 al 2 es igual y de sentido contrario a la fuerza con que atrae el cuerpo 2 al 1.

$\begin{array}{l} \vec{F_{12}} = - \vec{F_{21}} = G \frac{m_{1} m_{2}}{r^{2}} \hat{r} \\ \vec{r} = \vec{r_{2}} - \vec{r_{1}} \hat{r} = \frac{\vec{r}}{r} \end{array}$

Siendo $\vec{r}$ la posición relativa de la partícula 2 respecto de la 1

Restamos miembro a miembro las dos ecuaciones diferenciales

$\begin{array}{l} \frac{d^{2} \vec{r_{2}}}{d t^{2}} - \frac{d^{2} \vec{r_{1}}}{d t^{2}} = \frac{\vec{F_{21}}}{m_{2}} - \frac{\vec{F_{12}}}{m_{1}} = \\ \frac{d^{2} \vec{r}}{d t^{2}} = - G \frac{m_{1} m_{2}}{r^{2}} \hat{r} (\frac{1}{m_{2}} + \frac{1}{m_{1}}) \\ μ \frac{d^{2} \vec{r}}{d t^{2}} = - G \frac{m_{1} m_{2}}{r^{2}} \hat{r} μ = \frac{m_{1} m_{2}}{m_{1} + m_{2}} \end{array}$

Obtenemos una única ecuación diferencial que describe el movimiento de una partícula de masa reducida μ bajo la acción de la fuerza de atracción de un centro fijo que dista r de la partícula.

El centro de masas de un sistema aislado está en reposo o se mueve a lo largo de una línea recta con velocidad constante

Relacionamos la posición de cada una de las partículas con la posición del centro de masas $\vec{R}$ y la posición relativa $\vec{r}$ de la partícula 2 respecto de la 1

$\begin{array}{l} \vec{R} = \frac{m_{1} \vec{r_{1}} + m_{2} \vec{r_{2}}}{m_{1} + m_{2}} \\ \vec{r_{1}} = \vec{R} - \frac{m_{2}}{m_{1} + m_{2}} \vec{r} \vec{r_{2}} = \vec{R} + \frac{m_{1}}{m_{1} + m_{2}} \vec{r} \end{array}$

Derivando con respecto al tiempo obtenemos la velocidad del c.m. y de cada una de las partículas

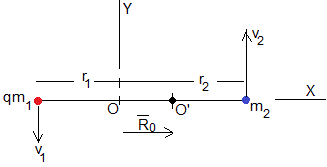
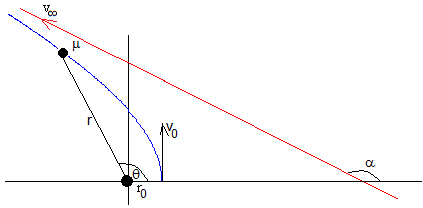
$\begin{array}{l} \vec{V_{c m}} = \frac{m_{1} \vec{v_{1}} + m_{2} \vec{v_{2}}}{m_{1} + m_{2}} \\ \vec{v_{1}} = \vec{V_{c m}} - \frac{m_{2}}{m_{1} + m_{2}} \vec{v} \vec{v_{2}} = \vec{V_{c m}} + \frac{m_{1}}{m_{1} + m_{2}} \vec{v} \end{array}$

Situación inicial

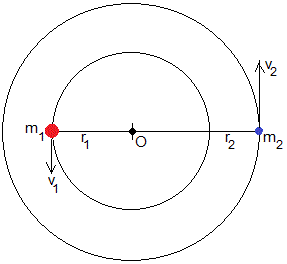
Supongamos dos estrellas de masas m₁ y m₂ que distan r₀ y se mueven en órbitas circulares de radio r₁ y r₂ alrededor de su centro de masas situado en el origen, $\vec{R} = 0$ , en reposo $\vec{V_{c m}} = 0$

Para que el centro de masa esté en el origen se tiene que cumplir que los vectores posición de los cuerpos r₁ y r₂ sean opuestos, sus módulos estarán relacionados

$\begin{array}{l} {\begin{cases} m_{1} r_{1} = m_{2} r_{2} \\ r_{1} + r_{2} = r_{0} \end{cases} \\ r_{1} = \frac{m_{2}}{m_{1} + m_{2}} r_{0} r_{2} = \frac{m_{1}}{m_{1} + m_{2}} r_{0} \end{array}$

Para que se conserve el momento lineal (o el centro de masas esté en reposo) los vectores velocidad de las partículas, v₁ y v₂ tienen que ser de signo opuesto y sus módulos estarán relacionados: m₁v₁=m₂v₂

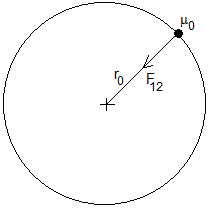
La partícula de masa reducida μ₀=m₁·m₂/(m₁+m₂) se mueve en una órbita circular de radio r₀ con velocidad constante v₀ bajo la acción de la fuerza de interacción mutua F₁₂

$μ_{0} \frac{v_{0}^{2}}{r_{0}} = G \frac{m_{1} m_{2}}{r_{0}^{2}} r_{0} = G \frac{m_{1} + m_{2}}{v_{0}^{2}}$

Donde $\vec{r_{0}} = \vec{r_{2}} - \vec{r_{1}}$ es la posición relativa del cuerpo 2 respecto de 1 y $\vec{v_{0}} = \vec{v_{2}} - \vec{v_{1}}$ , la velocidad relativa, sus módulos son: r₀=r₁+r₂, v₀=v₁+v₂

El periodo P₀ o tiempo que tardan en dar una vuelta completa es

$P_{0}^{2} = {(\frac{2 π r_{0}}{v_{0}})}^{2} = \frac{4 π^{2} r_{0}^{3}}{G (m_{1} + m_{2})}$

Como el centro de masas está en reposo en el origen, las posiciones de los cuerpos $\vec{r_{1}}$ y $\vec{r_{2}}$ y las velocidades $\vec{v_{1}}$ y $\vec{v_{2}}$ de cada una de las partículas serán

$\begin{array}{l} \vec{r_{1}} = - \frac{μ_{0}}{m_{1}} \vec{r_{0}} \vec{r_{2}} = \frac{μ_{0}}{m_{2}} \vec{r_{0}} \\ \vec{v_{1}} = - \frac{μ_{0}}{m_{1}} \vec{v_{0}} \vec{v_{2}} = \frac{μ_{0}}{m_{2}} \vec{v_{0}} \end{array}$

En un sistema aislado el momento lineal total permanece constante

$m_{1} \vec{v_{1}} + m_{2} \vec{v_{2}} = 0$

Coinciden la energía total y la relativa al c.m. en reposo

$E_{0} = \frac{1}{2} m_{1} v_{1}^{2} + \frac{1}{2} m_{2} v_{2}^{2} - G \frac{m_{1} m_{2}}{r_{0}} = \frac{1}{2} μ_{0} v_{0}^{2} - G \frac{m_{1} m_{2}}{r_{0}}$

Coinciden el momento angular total y el relativo al c.m. en reposo

$\vec{L_{0}} = m_{1} \vec{r_{1}} \times \vec{v_{1}} + m_{2} \vec{r_{2}} \times \vec{v_{2}} = μ_{0} \vec{r_{0}} \times \vec{v_{0}}$

Su módulo es L₀=μ₀r₀v₀, su dirección es perpendicular al plano de las órbitas circulares y su sentido es positivo

Consideremos un sistema binario formado por dos estrellas de masas m₁=3.15 y m₂=1.41 masas solares. La separación entre las estrellas es r₀=1.07 radios solares. Calculamos los radios r₁ y r₂ de sus órbitas circulares y las velocidades constantes v₁ y v₂

G=6.67e-11; %constante G
MS=1.98e30; %masa del Sol
RS=6.96e8; %radio del Sol
m2=1.41; %masas solares
m1=3.15;
%antes de la explosión
r0=1.07; %separación inicial entre las dos estrellas en radios del Sol
v0=sqrt(G*(m1+m2)*MS/(r0*RS)); %velocidad 
r1=m2*r0/(m1+m2); %radio de la órbita circular de 1
r2=m1*r0/(m1+m2); %radio de la órbita circular de 2
v1=m2*v0/(m1+m2); %velocidad de la estrella 1
v2=m1*v0/(m1+m2); %velocidad de la estrella 2

hold on
fplot(@(x) r1*cos(x),@(x) r1*sin(x),[0,2*pi], 'color','r')
fplot(@(x) r2*cos(x),@(x) r2*sin(x),[0,2*pi],'color','b')
plot (-r1,0,'o','markersize',8,'markeredgecolor','r','markerfacecolor','r')
plot (r2,0,'o','markersize',4,'markeredgecolor','b','markerfacecolor','b')
plot (0,0,'o','markersize',4,'markeredgecolor','k','markerfacecolor','k')
quiver(-r1,0,0,-v1/1e6,'color','r');
quiver(r2,0,0,v2/1e6,'color','b');
hold off
grid on
axis equal
xlabel('x')
ylabel('y')
title('Movimiento relativo tras la explosión')

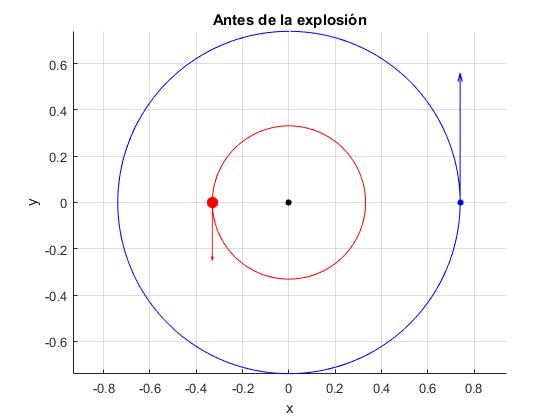
Situación inicial tras la explosión

Supongamos que la estrella de masa m₁ (de color rojo) pierde de forma instantánea una parte de su masa que ejecta de forma isótropa en dirección radial sin afectar a su compañera. Si la masa final de la estrella es q·m₁, vamos a ver cómo afecta al movimiento del sistema y de cada una de las dos partículas.

Posición y velocidad del centro de masas

La posición del centro de masas cambia tras la explosión

${\vec{R}}_{0} = \frac{q m_{1} \vec{r_{1}} + m_{2} \vec{r_{2}}}{q m_{1} + m_{2}} = μ_{0} \frac{(1 - q)}{q m_{1} + m_{2}} \vec{r_{0}}$

El centro de masas ya no permanece en reposo, la velocidad del centro de masas es constante (sistema aislado) e igual a

$\vec{V_{c m}} = \frac{q m_{1} \vec{v_{1}} + m_{2} \vec{v_{2}}}{q m_{1} + m_{2}} = μ_{0} \frac{(1 - q)}{q m_{1} + m_{2}} \vec{v_{0}}$

El centro de masas se mueve con velocidad constante $\vec{V_{c m}}$ desde la posición inicial $\vec{R_{0}}$

Expresamos el módulo de la velocidad del c.m. en términos del cociente x=m₁/m₂

$V_{c m} = \frac{m_{1} m_{2}}{m_{1} + m_{2}} \frac{(1 - q)}{q m_{1} + m_{2}} v_{0} = \frac{x (1 - q)}{(x + 1) (q x + 1)} v_{0}$

El máximo se obtiene derivando V_cm con respecto a x e igualando a cero

$\frac{d V_{c m}}{d x} = 0 x = \frac{1}{\sqrt{q}}$

Para este valor del cociente cociente m₁/m₂, la velocidad del c.m. V_cm vale

$V_{c m} = \frac{1 - \sqrt{q}}{1 - \sqrt{q}} v_{0}$

Momento angular después de la explosión relativo al nuevo c.m. O'

$\begin{array}{l} \vec{L_{c m}} = q m_{1} (\vec{r_{1}} - \vec{R_{0}}) \times \vec{v_{1}} + m_{2} (\vec{r_{2}} - \vec{R_{0}}) \times \vec{v_{2}} = \\ q m_{1} (- \frac{μ_{0}}{m_{1}} \vec{r_{0}} - μ_{0} \frac{(1 - q)}{q m_{1} + m_{2}} \vec{r_{0}}) \times (- \frac{μ_{0}}{m_{1}} \vec{v_{0}}) + m_{2} (\frac{μ_{0}}{m_{2}} \vec{r_{0}} - μ_{0} \frac{(1 - q)}{q m_{1} + m_{2}} \vec{r_{0}}) \times (\frac{μ_{0}}{m_{2}} \vec{v_{0}}) = \\ μ_{0} (\vec{r_{0}} \times \vec{v_{0}}) \frac{m_{1} m_{2}}{m_{1} + m_{2}} (\frac{q}{m_{1}} + q \frac{(1 - q)}{q m_{1} + m_{2}} + \frac{1}{m_{2}} - \frac{(1 - q)}{q m_{1} + m_{2}}) = q \frac{m_{1} + m_{2}}{q m_{1} + m_{2}} \vec{L_{0}} \end{array}$

El módulo del momento angular es

$L_{c m} = q \frac{m_{1} + m_{2}}{q m_{1} + m_{2}} μ_{0} r_{0} v_{0} = q \frac{m_{1} m_{2}}{q m_{1} + m_{2}} \sqrt{G (m_{1} + m_{2}) r_{0}}$

Energía después de la explosión relativa al nuevo cm. O'

$\begin{array}{l} E_{c m} = \frac{1}{2} q m_{1} v_{1}^{2} + \frac{1}{2} m_{2} v_{2}^{2} - G \frac{q m_{1} m_{2}}{r_{0}} - \frac{1}{2} (q m_{1} + m_{2}) V_{c m}^{2} = \\ \frac{1}{2} q m_{1} {(- \frac{μ_{0}}{m_{1}} v_{0})}^{2} + \frac{1}{2} m_{2} {(\frac{μ_{0}}{m_{2}} v_{0})}^{2} - G \frac{q m_{1} m_{2}}{r_{0}} - \frac{1}{2} (q m_{1} + m_{2}) {(\frac{(1 - q) μ_{0}}{q m_{1} + m_{2}} v_{0})}^{2} = \\ \frac{1}{2} μ_{0}^{2} v_{0}^{2} (\frac{q}{m_{1}} + \frac{1}{m_{2}}) - q μ_{0} v_{0}^{2} - \frac{1}{2} \frac{{(1 - q)}^{2} μ_{0}^{2}}{q m_{1} + m_{2}} v_{0}^{2} = \\ \frac{1}{2} μ_{0} v_{0}^{2} \frac{q (m_{1} - m_{2} - 2 q m_{1})}{q m_{1} + m_{2}} = \frac{1}{2} G \frac{q m_{1} m_{2}}{q m_{1} + m_{2}} \frac{(m_{1} - m_{2} - 2 q m_{1})}{r_{0}} \end{array}$

Llegamos al mismo resultado sabiendo que la partícula de masa reducida μ=qm₁m₂/(qm₁+m₂), parte de la posición r₀ con velocidad v₀

$E_{c m} = \frac{1}{2} μ v_{0}^{2} - G \frac{q m_{1} m_{2}}{r_{0}}$

Si m₁<m₂ entonces la energía E_cm<0 (trayectoria elíptica)
En el caso límite q=0, la energía E_cm=0 (trayectoria parabólica)
Si m₁>m₂ entonces la energía E_cm<0 (trayectoria elíptica) para (m₁-m₂-2qm₁)<0. O bien que, la masa perdida m₁-qm₁ sea menor que la masa que permanece después de la explosión qm₁+m₂
Si m₁>m₂ y se cumple la condición q<q_c, donde $q_{c} = \frac{1}{2} (1 - m_{2} / m_{1})$ , entonces la trayectoria es hiperbólica

Representamos

$\frac{E_{c m}}{\frac{1}{2} μ v_{0}^{2}} = \frac{q (\frac{m_{1}}{m_{2}} - 1 - 2 q \frac{m_{1}}{m_{2}})}{q \frac{m_{1}}{m_{2}} + 1}$

en función de q para varios valores del cociente m₁/m₂

hold on
for k=[0,0.3,1,3,10,100]
    f=@(x) x.*(k-1-2*k*x)./(k*x+1);
    fplot(f,[0,1],'displayName',num2str(k))
end
hold off
grid on
legend('-DynamicLegend','location','northeast')
xlabel('q')
ylabel('E')
title('Energía del c.m. después de la explosión')

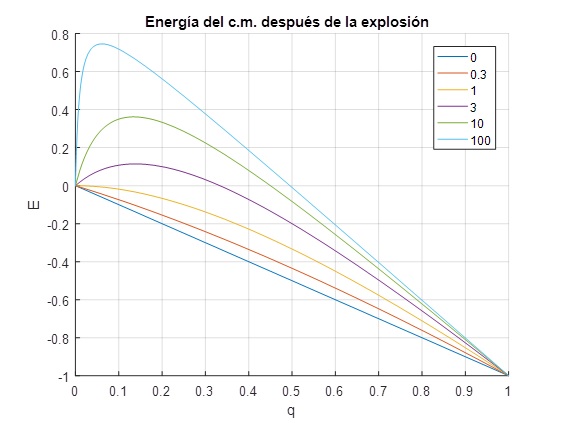
Para k=m₁/m₂<1 la energía E_cm es negativa (trayectoria elíptica), para m₁/m₂>1, la energía es positiva entre q=0 y q_c=(1-1/k)/2 (trayectoria hiperbólica) y negativa entre q_c y 1 (trayectoria elíptica)

Movimiento relativo de los cuerpos tras la explosión

Después de la explosión, la partícula de masa reducida μ=qm₁·m₂/(qm₁+m₂) bajo la acción de la fuerza central qm₁·m₂/r² describe una cónica cuyo parámetro d y excentricidad ε valen

$\begin{array}{l} r = \frac{d}{1 + ε \cos θ} \\ d = \frac{L_{c m}^{2}}{μ G q m_{1} m_{2}} ε = \sqrt{1 + \frac{2 L_{c m}^{2} E_{c m}}{μ {(G q m_{1} m_{2})}^{2}}} μ = \frac{q m_{1} m_{2}}{q m_{1} + m_{2}} \end{array}$

Introduciendo los valores de de la energía E_cm y del momento angular L_cm respecto del nuevo c.m.

$d = \frac{m_{1} + m_{2}}{q m_{1} + m_{2}} r_{0} ε = \frac{m_{1} (1 - q)}{q m_{1} + m_{2}}$

Por ejemplo, cuando ε<1 la órbita es elíptica o bien, m₁-qm₁<qm₁+m₂. La masa que pierde la estrella que explota tiene que ser menor que la masa que permanece después de la explosión, criterio que adelantamos en el apartado anterior

Trayectorias elípticas

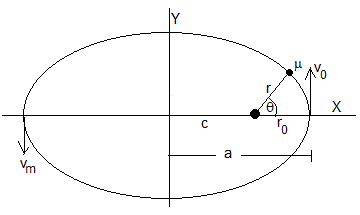
Para una órbita elíptica cuando θ=0, r=r₀ (distancia mímima al centro fijo de fuerzas) y cuando θ=π (distancia máxima)

$r_{m} = \frac{m_{1} + m_{2}}{(2 q - 1) m_{1} + m_{2}} r_{0}$

La velocidad relativa mínima v_m se obtiene aplicando la constancia del momento angular r₀v₀=r_mv_m

El semieje mayor de la elipse es a=(r₀+r_m)/2

$a = \frac{q m_{1} + m_{2}}{(2 q - 1) m_{1} + m_{2}} r_{0}$

Alternativamente, a través de la relación entre el semieje mayor a y la excentricidad ε

$\begin{array}{l} 2 a = \frac{d}{1 - ε} + \frac{d}{1 + ε} \\ a = \frac{d}{1 - ε^{2}} = \frac{q m_{1} + m_{2}}{(2 q - 1) m_{1} + m_{2}} r_{0} \end{array}$

El periodo es

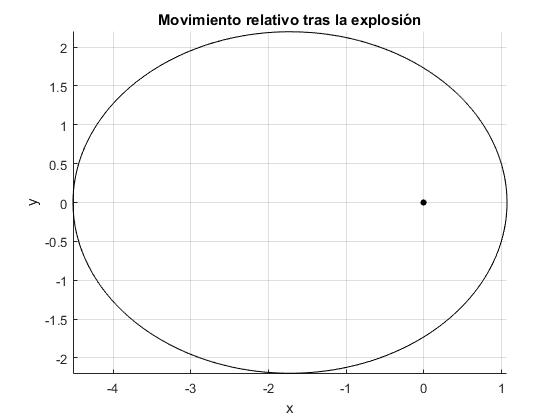
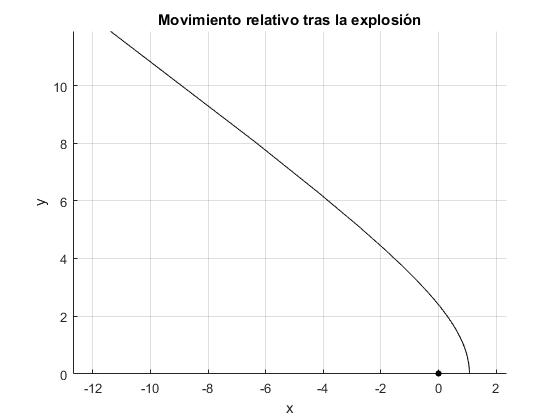
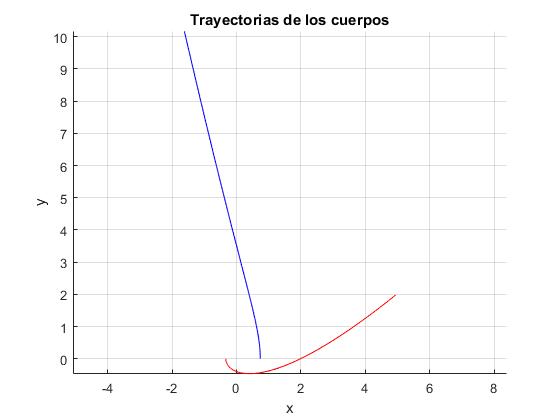
$\begin{array}{l} P^{2} = \frac{4 π^{2}}{G (q m_{1} + m_{2})} a^{3} \\ P^{2} = \frac{4 π^{2}}{G (q m_{1} + m_{2})} {(\frac{q m_{1} + m_{2}}{(2 q - 1) m_{1} + m_{2}})}^{3} r_{0}^{3} = \frac{(m_{1} + m_{2}) {(q m_{1} + m_{2})}^{2}}{{((2 q - 1) m_{1} + m_{2})}^{3}} P_{0}^{2} \end{array}$

La estrella masiva del sistema binario m₁=3.15 masas solares, explota, quedando reducida a una estrella de la misma masa que la compañera q·m₁=m₂=1.41. El valor de q=1.41/3.15=0.45 es mayor que el valor crítico, q_c=(1-m₂/m₁)/2=0.276. La excentricidad ε=0.617 es menor que la unidad. La partícula de masa reducida μ describe la elipse que se muestra en la figura, que corresponde al movimiento relativo de la partícula 2 respecto de la 1. La distancia más cercana al centro fijo de fuerzas (el origen) es r₀=1.07 y la más alejada r_m=4.52

m2=1.41; %masas solares
m1=3.15;
%antes de la explosión
r0=1.07; %separación inicial entre las dos estrellas en radios del Sol

q=1.41/3.15; %después de la explosión qm1=m2
Vcm=m1*m2*(1-q)*v0/((m1+m2)*(q*m1+m2)); %velocidad del c.m.
ex=m1*(1-q)/(q*m1+m2); %excentricidad
d=(m1+m2)*r0/(q*m1+m2); %parámetro d
a=d/(1-ex^2); %semieje mayor
rm=(m1+m2)*r0/((2*q-1)*m1+m2); %distancia máxima
r=@(x) d./(1+ex*cos(x));
hold on
fplot(@(x) r(x).*cos(x),@(x) r(x).*sin(x),[0,2*pi], 'color','k')
plot (0,0,'o','markersize',4,'markeredgecolor','k','markerfacecolor','k')
hold off
grid on
axis equal
xlabel('x')
ylabel('y')
title('Movimiento relativo tras la explosión')

Trayectorias hiperbólicas

La partícula de masa reducida μ parte de r₀ con velocidad v₀ y luego, se aleja hacia el infinito (la energía potencial es cero). La velocidad final v_∞ es

$\begin{array}{l} E_{c m} = \frac{1}{2} μ v_{0}^{2} - \frac{G q m_{1} m_{2}}{r_{0}} = \frac{1}{2} μ v_{\infty}^{2} \\ \frac{1}{2} \frac{m_{1} m_{2}}{m_{1} + m_{2}} v_{0}^{2} \frac{q (m_{1} - m_{2} - 2 q m_{1})}{q m_{1} + m_{2}} = \frac{1}{2} \frac{q m_{1} m_{2}}{q m_{1} + m_{2}} v_{\infty}^{2} \\ v_{\infty} = v_{0} \sqrt{\frac{m_{1} - m_{2} - 2 q m_{1}}{m_{1} + m_{2}}} \end{array}$

Poniendo r=∞ en la ecuación de la trayectoria, obtenemos el ángulo α de la asíntota, cosα=-1/ε

Consideremos ahora el caso de que el factor q<q_c. Por ejemplo q=0.2. La excentricidad es ε=1.23 mayor que la unidad. La partícula de masa reducida μ describe la hipérbola que se muestra en la figura, que corresponde al movimiento relativo de la partícula 2 respecto de la 1. El ángulo para el cual r→∞ es α=2.51 (144°). La distancia más cercana al centro fijo de fuerzas (el origen) es r₀=1.07

m2=1.41; %masas solares
m1=3.15;
%antes de la explosión
r0=1.07; %separación inicial entre las dos estrellas en radios del Sol

qc=(1-m2/m1)/2; % valor crítico q>qc (elíptica), q<qc (hiperbólica)
q=0.2; %después de la explosión qm1=m2
Vcm=m1*m2*(1-q)*v0/((m1+m2)*(q*m1+m2)); %velocidad del c.m.
ex=m1*(1-q)/(q*m1+m2); %excentricidad
d=(m1+m2)*r0/(q*m1+m2); %parámetro d
alfa=acos(-1/ex);
r=@(x) d./(1+ex*cos(x));
hold on
fplot(@(x) r(x).*cos(x),@(x) r(x).*sin(x),[0,alfa-0.1], 'color','k')
plot (0,0,'o','markersize',4,'markeredgecolor','k','markerfacecolor','k')
hold off
grid on
axis equal
xlabel('x')
ylabel('y')
title('Movimiento relativo tras la explosión')

Movimiento del centro de masas

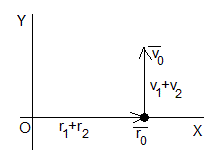
Como ya se ha mencionado, el centro de masas se mueve con velocidad constante (sistema aislado) $\vec{V_{c m}}$ desde la posición inicial $\vec{R_{0}}$ , la ecuación del movimiento es

$\begin{array}{l} \vec{r_{c m}} = \vec{R_{0}} + \vec{V_{c m}} t \\ \vec{r_{c m}} = μ_{0} \frac{(1 - q)}{q m_{1} + m_{2}} \vec{r_{0}} + μ_{0} \frac{(1 - q)}{q m_{1} + m_{2}} \vec{v_{0}} \cdot t \end{array}$

En la figura se muestran los vectores $\vec{r_{0}}$ y $\vec{v_{0}}$

Movimiento de cada uno de los cuerpos

Conocida la posición del centro de masas $\vec{r_{c m}}$ en función del tiempo t y la posición relativa $\vec{r}$ del cuerpo 2 respecto del 1, determinamos la posición de cada uno de los cuerpos

$\begin{array}{l} {\begin{cases} \vec{r_{c m}} = \frac{q m_{1} {\vec{r}}_{1} + m_{2} \vec{r_{2}}}{q m_{1} + m_{2}} \\ \vec{r} = \vec{r_{2}} - \vec{r_{1}} \end{cases} \\ \vec{r_{1}} = \vec{r_{c m}} - \frac{m_{2}}{q m_{1} + m_{2}} \vec{r} \vec{r_{2}} = \vec{r_{c m}} + \frac{q m_{1}}{q m_{1} + m_{2}} \vec{r} \end{array}$

Las coordenadas (x₁, y₁) del cuerpo de masa m₁ y las coordenadas (x₂, y₂) del cuerpo de masa m₂ en función del tiempo t son, respectivamente

$\begin{array}{l} \vec{r_{1}} {\begin{cases} x_{1} = \frac{m_{1} m_{2}}{m_{1} + m_{2}} \frac{(1 - q)}{q m_{1} + m_{2}} r_{0} - \frac{m_{2}}{q m_{1} + m_{2}} (\frac{d}{1 + ε \cos θ}) \cos θ \\ y_{1} = \frac{m_{1} m_{2}}{m_{1} + m_{2}} \frac{(1 - q)}{q m_{1} + m_{2}} v_{0} \cdot t - \frac{m_{2}}{q m_{1} + m_{2}} (\frac{d}{1 + ε \cos θ}) \sin θ \end{cases} \\ \vec{r_{2}} {\begin{cases} x_{2} = \frac{m_{1} m_{2}}{m_{1} + m_{2}} \frac{(1 - q)}{q m_{1} + m_{2}} r_{0} + \frac{q m_{1}}{q m_{1} + m_{2}} (\frac{d}{1 + ε \cos θ}) \cos θ \\ y_{2} = \frac{m_{1} m_{2}}{m_{1} + m_{2}} \frac{(1 - q)}{q m_{1} + m_{2}} v_{0} \cdot t + \frac{q m_{1}}{q m_{1} + m_{2}} (\frac{d}{1 + ε \cos θ}) \sin θ \end{cases} \end{array}$

Donde la posición angular θ es una función del tiempo t a través de la ecuación de Kepler, que hay que resolver empleando procedimientos numéricos, como vamos a ver en los ejemplos

Del mismo modo, obtenemos la velocidad de los cuerpos

$\vec{v_{1}} = \vec{V_{c m}} - \frac{m_{2}}{q m_{1} + m_{2}} \vec{v} \vec{v_{2}} = \vec{V_{c m}} + \frac{q m_{1}}{q m_{1} + m_{2}} \vec{v}$

Si m₁<m₂ o si m₁>m₂ y q>q_c

El movimiento relativo de los dos cuerpos describe una trayectoria elíptica ε<1.

$r = \frac{d}{1 + ε \cos θ}$

Partimos de la constancia del momento angular relativo al c.m. para la partícula de masa reducida μ

$L_{c m} = μ r^{2} \frac{d θ}{d t}$

Integrando, obtenemos la expresión de la posición angular θ en función del tiempo t.

$\int_{0}^{θ} \frac{d θ}{{(1 + ε \cos θ)}^{2}} = \frac{L_{c m}}{μ d^{2}} t$

La integral está resuelta en la página titulada la ecuación de Kepler

$E + ε \sin E = {(1 - ε^{2})}^{3 / 2} \frac{L_{c m}}{μ d^{2}} t$

Dado el tiempo t calculamos el ángulo θ del siguiente modo:

Calculamos M_e=2πt/P. Donde P es el periodo y a el semieje mayor de la elipse

$P^{2} = \frac{4 π^{2}}{G (q m_{1} + m_{2})} a^{3}$

Resolvemos la ecuación transcendente, E-ε·sinE=M_e
Calculamos la posición ángular θ

$\tan (\frac{θ}{2}) = \sqrt{\frac{1 + ε}{1 - ε}} \tan (\frac{E}{2})$

G=6.67e-11; %constante G
MS=1.98e30; %masa del Sol
RS=6.96e8; %radio del Sol
m2=1.41; %masas solares
m1=3.15;
%antes de la explosión
r0=1.07; %separación inicial entre las dos estrellas en radios del Sol
v0=sqrt(G*(m1+m2)*MS/(r0*RS)); %velocidad 

q=1.41/3.15; %después de la explosión qm1=m2
ex=m1*(1-q)/(q*m1+m2); %excentricidad
d=(m1+m2)*r0/(q*m1+m2); %parámetro d
a=d/(1-ex^2); %semieje mayor
P=2*pi*(a*RS)^(3/2)/sqrt(G*(q*m1+m2)*MS); %periodo
Vcm=m1*m2*(1-q)*v0/((m1+m2)*(q*m1+m2)); %velocidad del c.m.
R0cm=m1*m2*(1-q)*r0/((m1+m2)*(q*m1+m2)); %posición inicial del c.m.

x1=zeros(0,50);
y1=zeros(0,50);
x2=zeros(0,50);
y2=zeros(0,50);
i=1;
th=0;
for t=linspace(0,2*P,200) %cambiar el tiempo final 2*P, 3*P, etc.
%dado el tiempo calculamos la posición angular 
    Me=2*pi*t/P;
    E0=Me-ex/2;
    f=@(x) x-ex*sin(x)-Me;
    E=fzero(f,E0);
    th=2*atan(sqrt((1+ex)/(1-ex))*tan(E/2));
    if th<0
        th=th+2*pi;
    end
%posición (coordenadas x e y) de cada uno de los cuerpos    
    x1(i)=R0cm-m2*(d/(1+ex*cos(th)))*cos(th)/(q*m1+m2);
    y1(i)=Vcm*t/RS-m2*(d/(1+ex*cos(th)))*sin(th)/(q*m1+m2);
    x2(i)=R0cm+q*m1*(d/(1+ex*cos(th)))*cos(th)/(q*m1+m2);
    y2(i)=Vcm*t/RS+q*m1*(d/(1+ex*cos(th)))*sin(th)/(q*m1+m2);
    i=i+1;
end
hold on
plot(x1,y1,'r')
plot(x2,y2,'b')
hold off
axis equal
grid on
xlabel('x')
ylabel('y')
title('Trayectorias de los cuerpos')

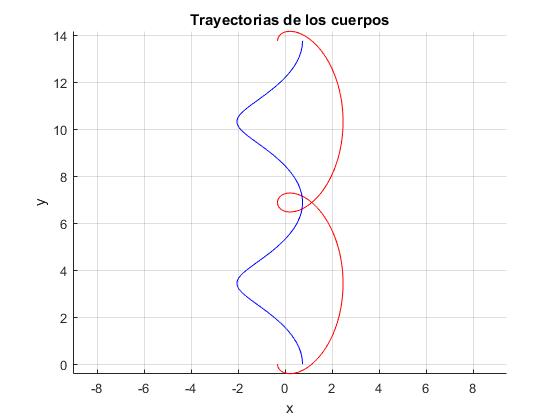
Si m₁>m₂ y q<q_c

El movimiento relativo de los dos cuerpos describe una trayectoria hiperbólica ε>1.

$r = \frac{d}{1 + ε \cos θ}$

Dado el tiempo t calculamos el ángulo θ mediante la ecuación de Kepler

La ecuación de Kepler para el problema de dos cuerpos con trayectorias hiperbólicas, se escribe

$\begin{array}{l} ε \sinh F - F = {(ε^{2} - 1)}^{3 / 2} \frac{L_{c m}}{μ d^{2}} t \\ ε \sinh F - F = {(\frac{ε^{2} - 1}{d})}^{3 / 2} \sqrt{G (q m_{1} + m_{2})} t \end{array}$

Teniendo en cuenta los valores del parámetro d y de la excentricidad ε

$ε \sinh F - F = \sqrt{G} \frac{{(m_{1} - m_{2} - 2 q m_{1})}^{3 / 2}}{(q m_{1} + m_{2})} \frac{1}{r_{0}^{3 / 2}} t$

dado el tiempo t, resolvemos la ecuación transcendente en F. Conocido F despejamos la posición angular θ

$\tanh (\frac{F}{2}) = \sqrt{\frac{ε - 1}{ε + 1}} \tan (\frac{θ}{2})$

G=6.67e-11; %constante G
MS=1.98e30; %masa del Sol
RS=6.96e8; %radio del Sol
m2=1.41; %masas solares
m1=3.15;
%antes de la explosión
r0=1.07; %separación inicial entre las dos estrellas en radios del Sol
v0=sqrt(G*(m1+m2)*MS/(r0*RS)); %velocidad 

q=0.2; %trayectorias hiperbólicas
ex=m1*(1-q)/(q*m1+m2); %excentricidad
d=(m1+m2)*r0/(q*m1+m2); %parámetro d
Vcm=m1*m2*(1-q)*v0/((m1+m2)*(q*m1+m2)); %velocidad del c.m.
R0cm=m1*m2*(1-q)*r0/((m1+m2)*(q*m1+m2)); %posición inicial del c.m.
alfa=acos(-1/ex); %ángulo límite (asíntota)
%valor cercano al límite de F 
F1=2*atanh(sqrt((ex-1)/(ex+1))*tan((alfa-0.02)/2));
x1=zeros(0,50);
y1=zeros(0,50);
x2=zeros(0,50);
y2=zeros(0,50);
i=1;
th=0;
for t=linspace(0,20*RS/v0,200)
 %dado el tiempo calculamos la posición angular 
   Me=sqrt(MS*G/(r0*RS)^3)*(m1-m2-2*q*m1)^(3/2)*t/(q*m1+m2);
    f=@(x) ex*sinh(x)-x-Me;
    E=fzero(f,[0,F1]);
    th=2*atan(sqrt((1+ex)/(ex-1))*tanh(E/2));
    
 %posición (coordenadas x e y) de cada uno de los cuerpos    
    x1(i)=R0cm-m2*(d/(1+ex*cos(th)))*cos(th)/(q*m1+m2);
    y1(i)=Vcm*t/RS-m2*(d/(1+ex*cos(th)))*sin(th)/(q*m1+m2);
    x2(i)=R0cm+q*m1*(d/(1+ex*cos(th)))*cos(th)/(q*m1+m2);
    y2(i)=Vcm*t/RS+q*m1*(d/(1+ex*cos(th)))*sin(th)/(q*m1+m2);
    i=i+1;
end
hold on
plot(x1,y1,'r')
plot(x2,y2,'b')
hold off
axis equal
grid on
xlabel('x')
ylabel('y')
title('Trayectorias de los cuerpos')

Las velocidades finales de los cuerpos son

$\begin{array}{l} \vec{v_{1 \infty}} = \vec{V_{c m}} - \frac{m_{2}}{q m_{1} + m_{2}} \vec{v_{\infty}} \vec{v_{2 \infty}} = \vec{V_{c m}} + \frac{q m_{1}}{q m_{1} + m_{2}} \vec{v_{\infty}} \\ {\begin{cases} \vec{v_{1 \infty}} = μ_{0} \frac{(1 - q)}{q m_{1} + m_{2}} v_{0} \hat{j} - \frac{m_{2}}{q m_{1} + m_{2}} (v_{\infty} \cos α \cdot \hat{i} + v_{\infty} \sin α \cdot \hat{j}) \\ \vec{v_{2 \infty}} = μ_{0} \frac{(1 - q)}{q m_{1} + m_{2}} v_{0} \hat{j} + \frac{q m_{1}}{q m_{1} + m_{2}} (v_{\infty} \cos α \cdot \hat{i} + v_{\infty} \sin α \cdot \hat{j}) \end{cases} \\ {\begin{cases} \vec{v_{1 \infty}} = (\frac{m_{2}}{q m_{1} + m_{2}} \frac{1}{ε} v_{\infty}) \hat{i} + (μ_{0} \frac{(1 - q)}{q m_{1} + m_{2}} v_{0} - \frac{m_{2}}{q m_{1} + m_{2}} v_{\infty} \sqrt{1 - \frac{1}{ε^{2}}}) \hat{j} \\ \vec{v_{2 \infty}} = (- \frac{q m_{1}}{q m_{1} + m_{2}} \frac{1}{ε} v_{\infty}) \hat{i} + (μ_{0} \frac{(1 - q)}{q m_{1} + m_{2}} v_{0} + \frac{q m_{1}}{q m_{1} + m_{2}} v_{\infty} \sqrt{1 - \frac{1}{ε^{2}}}) \hat{j} \end{cases} \end{array}$

Introduciendo los valores del módulo de la velocidad relativa cuando r→∞, v_∞ y la excentricidad ε

${\begin{cases} \vec{v_{1 \infty}} = (\frac{m_{2}}{m_{1} (1 - q)} v_{\infty}) \hat{i} + (\frac{m_{2} (q m_{1} + m_{2})}{(m_{1} + m_{2}) m_{1} (1 - q)} v_{0}) \hat{j} \\ \vec{v_{2 \infty}} = (- \frac{q}{1 - q} v_{\infty}) \hat{i} + (\frac{(m_{1} - 2 q m_{1} - q m_{2})}{(m_{1} + m_{2}) (1 - q)} v_{0}) \hat{j} \end{cases}$

Utilizamos el producto escalar para calcular el ángulo β entre los dos vectores

$\begin{array}{l} \vec{v_{1 \infty}} \cdot \vec{v_{2 \infty}} = v_{1 \infty} v_{2 \infty} \cos β \\ \cos β = \frac{m_{2}}{\sqrt{m_{1}^{2} - 2 q m_{1} (m_{1} + m_{2})}} \end{array}$

Math Symbolic de MATLAB nos ayuda a realizar las largas operaciones algebraicas

>> syms m1 m2 q;
>> ux=-q*sqrt((m1-m2-2*q*m1)/(m1+m2))/(1-q);
>> vx=m2*sqrt((m1-m2-2*q*m1)/(m1+m2))/(m1*(1-q));
>> uy=(m1-2*q*m1-q*m2)/((m1+m2)*(1-q));
>> vy=m2*(q*m1+m2)/(m1*(1-q)*(m1+m2));
%producto escalar
>> pe=ux*vx+uy*vy;  
>> simplify(pe)
ans =m2^2/(m1 + m2)^2
%poducto de los módulos de los dos vectores
>> mo=sqrt(ux^2+uy^2)*sqrt(vx^2+vy^2); 
>> simplify(mo)
ans =(m2^2/(m1 + m2)^2)^(1/2)*(-(m1*(2*m1*q - m1 + 2*m2*q))/(m1 + m2)^2)^(1/2)

Después de correr el script, comprobamos que el ángulo entre los vectores $\vec{v_{1 \infty}}$ y $\vec{v_{2 \infty}}$ es β

>> v_inf=v0*sqrt((m1-m2-2*q*m1)/(m1+m2)); %velocidad en el infinito
>> ux=m2*v_inf/(m1*(1-q)); %componentes v1_infinito
>> uy=m2*(q*m1+m2)*v0/(m1*(m1+m2)*(1-q));
>> vx=-q*v_inf/(1-q); %componentes v2_infinito
>> vy=(m1-2*q*m1-q*m2)*v0/((m1+m2)*(1-q));
>> fi=(pi+atan(vy/vx)-atan(uy/ux))*180/pi %ángulo entre los dos vectores
fi =   46.3771
>> beta=acos(m2/sqrt(m1^2-2*q*m1*(m1+m2)))*180/pi %mediante la fórmula
beta =   46.3771

Actividades

Se introduce

La masa m₁ del primer cuerpo en el control titulado Masas: m₁
La masa m₂ de segundo cuerpo en el control titulado Masas: m₂
q·m₁ es la masa final de la estrella que explota, donde q es un factor entre 0 y 1, que se introduce en el control titulado Proporción q
Se ha fijado la distancia entre los cuerpos en r₀=10 unidades
Se ha establecido un sistema de unidades de masas y distancias de modo que el valor de la constante G=1
Para ver mejor las trayectorias de los cuerpos se puede cambiar la escala, en el control titulado Escala

El programa interactivo, empieza mostrando los dos cuerpos (rojo de masa m₁ y azul de masa m₂), separados r₀=10, girando con la misma velocidad angular, alrededor del origen.

Cuando han completado una vuelta, el cuerpo de color rojo explota, perdiendo masa. Su masa final es q·m₁. Se observa la trayectoria de cada uno de los cuerpos y el movimiento rectilíneo del centro de masas.

Se proporcionan los datos de la excentricidad de la cónica que describe la partícula de masa reducida μ y la velocidad del centro de masas

Masas: m₁ m₂
Proporción q: Escala :

Referencias

R. Mitalas. Supernovae in binary systems: An application of classical mechanics. Am. J. Phys. 48(3), March 1980. pp. 226-231