El fenómenos de las mareas

El origen de las fuerzas de marea

El origen de las fuerza de marea se debe a que la Tierra es un cuerpo extenso y el campo gravitatorio producido por la Luna o por el Sol no es homogéneo en todos sus puntos, ya que hay unos puntos que están más cercanos y otros más alejados de dichos cuerpos celestes.

Supondremos que la Tierra es un cuerpo rígido de forma esférica de radio R, que está cubierta por una capa de agua de espesor uniforme y de pequeña profundidad. El cuerpo perturbador, la Luna o el Sol se supone que está en el plano ecuatorial de la Tierra

Aunque el Sol y la Luna se mueven, se considera que el agua está en todo momento en equilibrio, la velocidad y la aceleración de cualquier elemento de líquido respecto de la Tierra se supone despreciable.

Supondremos inicialmente, que el cuerpo perturbador es la Luna, las mismas fórmulas serán aplicables para el Sol. Finalmente, analizaremos el efecto combinado de la Luna y del Sol.

Consideremos la Tierra y la Luna inmóviles en el espacio estando sus centros separados una distancia r. La fuerza de marea, en una determinada posición P de la superficie de la Tierra, es igual a la diferencia entre la fuerza de atracción que la Luna ejerce sobre un objeto situado en dicha posición y la fuerza de atracción que ejercería sobre tal objeto si estuviese en el centro de la Tierra.

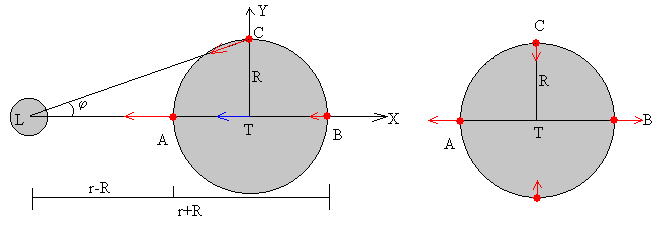
Dibujamos las fuerzas de atracción que ejerce la Luna (en color rojo) sobre un objeto de masa m situado en los puntos A, B y C y la fuerza que ejercería (en color azul) sobre dicho objeto si estuviese situado en el centro T de la Tierra. A la derecha, se dibujan las fuerzas de marea (diferencia entre los vectores rojos y azul) en los puntos A, B y C.

En el centro de la Tierra T, la fuerza de atracción está dirigida hacia el centro de la Luna

$\vec{F_{T}} = - G \frac{M m}{r^{2}} \hat{i}$

En A, la fuerza de atracción que ejerce la Luna sobre un objeto de masa m es

$\vec{F_{A}} = - G \frac{M m}{{(R - r)}^{2}} \hat{i}$

y la fuerza de marea en dicho punto es

$\vec{f_{A}} = \vec{F_{A}} - \vec{F_{T}} = - G M m (\frac{1}{{(r - R)}^{2}} - \frac{1}{r^{2}}) \hat{i} \approx - G M m \frac{2 R}{r^{3}} \hat{i}$

Se ha hecho la aproximación R<<r, el radio de la Tierra R=6.37·10⁶ m es mucho menor que la distancia entre el centro de la Tierra y el centro de la Luna r=384.4·10⁶ m

En B, la fuerza de marea es

$\vec{f_{B}} = \vec{F_{B}} - \vec{F_{T}} = - G M m (\frac{1}{{(r + R)}^{2}} - \frac{1}{r^{2}}) \hat{i} \approx G M m \frac{2 R}{r^{3}} \hat{i}$

En C, la fuerza de atracción es

$\vec{F_{C}} = - G \frac{M m}{R^{2} + r^{2}} (\cos φ \hat{i} + \sin φ \hat{j})$

Teniendo en cuenta que el ángulo φ es muy pequeño, tan φ=R/r, con R=6.37·10⁶ m, y r=384.4·10⁶ m, φ=0.017 rad. Por lo que cos φ≈1, y sin φ≈tan φ=R/r

$\vec{f_{C}} = \vec{F_{C}} - \vec{F_{T}} = G M m \frac{2 R}{r^{3}} \hat{j}$

Las fuerzas de marea en las posiciones A y B, en la línea que une la Luna y la Tierra son aproximadamente el doble en módulo, que en la posición C, perpendicular a dicha línea.

En P, la fuerza de marea es.

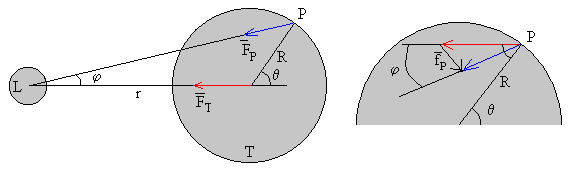
La fuerza que ejerce la Luna sobre un objeto de masa m situado en el punto P distante r_P del centro de la Luna será

$F_{P} = G \frac{M m}{r_{P}^{2}}$

y está dirigida según la línea que une el punto P con el centro de la Luna

La fuerza de marea en P es la diferencia entre los vectores $\vec{f_{P}} = \vec{F_{P}} - \vec{F_{T}}$ . Sea

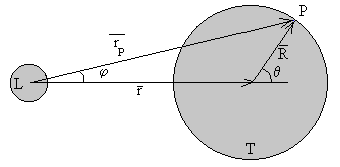
$\vec{r_{P}}$ el vector con origen en el centro de la Luna y extremo en P
$\vec{r}$ es el vector con origen en la Luna y extremo en el centro de la Tierra
$\vec{R}$ el vector con origen en la Tierra y extremo en el punto P

$\begin{array}{l} \vec{r_{P}} = \vec{r} + \vec{R} \\ \begin{array}{l} \vec{f_{P}} = - G M m (\frac{{\vec{r}}_{P}}{r_{P}^{3}} - \frac{\vec{r}}{r^{3}}) = - G M m (\frac{\vec{r} + \vec{R}}{r_{P}^{3}} - \frac{\vec{r}}{r^{3}}) \\ r_{P}^{2} = {(\vec{r} + \vec{R})}^{2} = r^{2} + R^{2} + 2 \vec{r} \cdot \vec{R} \approx r^{2} (1 + \frac{2 \vec{r} \cdot \vec{R}}{r^{2}}) \\ \begin{array}{l} \vec{f_{P}} \approx - \frac{G M m}{r^{3}} ((\vec{r} + \vec{R}) {(1 + \frac{2 \vec{r} \cdot \vec{R}}{r^{2}})}^{- 3 / 2} - \vec{r}) \approx \\ - \frac{G M m}{r^{3}} ((\vec{r} + \vec{R}) (1 - \frac{3 \vec{r} \cdot \vec{R}}{r^{2}}) - \vec{r}) \approx \end{array} \\ - \frac{G M m}{r^{3}} (\vec{R} - r \frac{3 \vec{r} \cdot \vec{R}}{r^{2}}) \end{array} \end{array}$

Para θ=0, los vectores $\vec{r}, \vec{R}$ tienen la misma dirección y sentido, obtenemos $\vec{f_{B}}$ (véase la primer figura)
Para θ=π/2 los vectores $\vec{r}, \vec{R}$ son perpendiculares, el producto escalar es cero, obtenemos $\vec{f_{C}}$
Para θ=π, los vectores $\vec{r}, \vec{R}$ tienen la misma dirección y pero sentido opuesto, obtenemos $\vec{f_{A}}$

Como apreciamos en la figura, solamente tenemos que calcular las fuerzas de marea en la mitad de la Tierra por encima del eje que une el centro de la Tierra y el centro de la Luna. Los puntos de la Tierra simétricos, por debajo de dicho eje, tienen fuerzas de marea iguales y de sentido contrario.

Componentes de la fuerza de marea.

Para calcular la componente radial de la fuerza de marea, hacemos el producto escalar $\vec{f_{P}} \cdot \vec{R} = f_{R} R$ , donde f_R es la componente radial de la fuerza de marea

$f_{R} = \frac{G M m}{r^{3}} R (3 \cos^{2} θ - 1)$

La componente tangencial f_t se calcula mediante el módulo del producto vectorial $| \vec{f_{P}} \times \vec{R} | = f_{t} R$

$f_{t} = - 3 \frac{G M m}{r^{3}} R sin θ \cos θ$

La componente tangencial es cero, para θ=0, punto B, θ=90º punto C, θ=180º punto A.
La componente radial es máxima, para θ=0, punto B, θ=180º punto A. Es mínima, para θ=90º, punto C.

Datos

Masa de la Luna, M=7.35·10²² kg
Distancia media entre el centro de la Tierra y el centro de la Luna, r=384.4·10⁶ m
Masa del Sol, M=1.98·10³⁰ kg
Distancia media entre el centro de la Tierra y el centro del Sol, r=149.6·10⁹ m
Radio de la Tierra, R=6.37·10⁶ m
Constante G=6.67·10^-11 Nm²/kg²

La fuerza de atracción que ejerce la Tierra sobre un objeto de masa m situado en su superficie es

$F = \frac{G M_{T} m}{R^{2}} = \frac{6.67 \cdot 10^{- 11} \cdot 5.98 \cdot 10^{24} \cdot m}{{(6.37 \cdot 10^{6})}^{2}} = 9.83 \cdot m N$

El Sol está muy alejado de la Tierra, pero tiene una masa enorme. La Luna está cercana a la Tierra pero su masa es relativamente pequeña. La fuerza de atracción que ejerce el Sol sobre el c.m. de la Tierra es mayor que la fuerza que ejerce la Luna sobre el c.m. de la Tierra.

$\begin{array}{l} F_{L} = \frac{G M_{L} m}{r^{2}} = \frac{6.67 \cdot 10^{- 11} \cdot 7.35 \cdot 10^{22} \cdot m}{{(384.4 \cdot 10^{6})}^{2}} = 3.32 \cdot 10^{- 5} \cdot m N \\ F_{S} = \frac{G M_{S} m}{r^{2}} = \frac{6.67 \cdot 10^{- 11} \cdot 1.98 \cdot 10^{30} \cdot m}{{(149.6 \cdot 10^{9})}^{2}} = 5.90 \cdot 10^{- 3} \cdot m N \end{array}$

El cociente es F_S/F_L=178

Estimados el valor máximo de las fuerzas de marea en A o B (θ=0), véase la primera figura

Debidas a la Luna

$f_{L} = 2 \frac{G M_{L}}{r^{2}} \frac{R}{r} = 2 \frac{6.67 \cdot 10^{- 11} \cdot 7.35 \cdot 10^{22} \cdot 6.37 \cdot 10^{6} \cdot m}{{(384.4 \cdot 10^{6})}^{3}} = 1.1 \cdot 10^{- 6} \cdot m N$

Debidas al Sol

$f_{S} = 2 \frac{G M_{S}}{r^{2}} \frac{R}{r} = 2 \frac{6.67 \cdot 10^{- 11} \cdot 1.98 \cdot 10^{30} \cdot 6.37 \cdot 10^{6} \cdot m}{{(149.6 \cdot 10^{9})}^{3}} = 5.02 \cdot 10^{- 7} \cdot m N$

El cociente entre estas dos fuerzas es f_L/f_S=2.195

Estas cifras nos indican que, las fuerzas de marea son muy pequeñas comparadas con la fuerza de atracción de la Tierra 9.83·m sobre un objeto de masa m situado en su superficie, pero sus efectos son notables.

La fuerza de atracción del Sol sobre el c.m. de la Tierra es mayor que la fuerza de atracción de la Luna, a pesar de que ésta está muy próxima a la Tierra. Sin embargo, la fuerza de marea producida por el Sol es más pequeña que la producida por la Luna.

Elevación de la capa de agua

El siguiente paso, cuya demostración se omite, por razones de dificultad matemática, pero que puede consultarse en el primer artículo citado en las referencias, es el cálculo de la energía potencial correspondiente a la fuerza de marea $\vec{f_{P}}$ .

La forma S₀ de la superficie debido a la fuerza de atracción de la Tierra y a su rotación es la de un esferoide de revolución alrededor del eje polar.

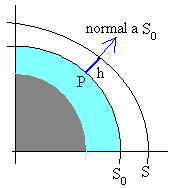
La fuerza centrípeta, debida a la rotación de la Tierra alrededor de su eje, que es una fuerza independiente del tiempo, no añade nada a las fuerzas de marea.

El efecto del cuerpo perturbador (Sol, Luna o ambos) es el distorsionar ligeramente la superficie S₀, para dar lugar a una nueva superficie S, donde S es una superficie equipotencial perpendicular a la resultante de todas las fuerzas, incluidas las de marea, que actúan en P.

Teniendo en cuenta, que el volumen de agua que cubre la Tierra permanece constante, se determina la elevación h del punto P de la superficie S₀ debida exclusivamente a las fuerzas de atracción del cuerpo perturbador.

$h = \frac{M}{2 M_{T}} {(\frac{R}{r})}^{3} R (3 \cos^{2} θ - 1)$

donde M es la masa del cuerpo perturbador, M_T=5.98·10²⁴ kg es la masa de la Tierra, R su radio, r la distancia entre el centro de la Tierra y el centro del cuerpo perturbador.

Esta es la expresión que emplearemos en los programas interactivos al final de esta página, donde hemos supuesto que el cuerpo perturbador está en reposo en el plano ecuatorial de la Tierra a una distancia r de su centro.

La máxima elevación corresponde al ángulo θ=0º o θ=π, cuando el cuerpo perturbador está delante o detrás, (puntos A y B de la primera figura) donde son máximas las fuerzas de marea.

La mínima elevación corresponde al ángulo θ=π/2, (punto C de la primera figura). La máxima elevación es el doble en valor absoluto, de la mínima elevación. De modo que, la diferencia entre altura máxima de la bajamar y la pleamar es

$Δ h_{m á x} = 3 \frac{M}{2 M_{T}} {(\frac{R}{r})}^{3} R$

Con los datos proporcionados en el apartado anterior. Para las mareas producidas por la Luna

$Δ h_{m á x} = 3 \frac{7.35 \cdot 10^{22}}{2 \cdot 5.98 \cdot 10^{24}} \frac{{(6.37 \cdot 10^{6})}^{4}}{{(384.4 \cdot 10^{6})}^{3}} = 53.4 cm$

Para las mareas producidas por el Sol

$Δ h_{m á x} = 3 \frac{1.98 \cdot 10^{30}}{2 \cdot 5.98 \cdot 10^{24}} \frac{{(6.37 \cdot 10^{6})}^{4}}{{(149.6.4 \cdot 10^{9})}^{3}} = 24.4 cm$

Mareas producidas por el Sol y la Luna

Cuando consideramos los efectos combinado de la de la Luna y del Sol, la elevación de la marea se obtiene sumando las elevaciones debidas cada uno de ellos.

$h = \frac{M_{L}}{2 M_{T}} {(\frac{R}{r_{L}})}^{3} R (3 \cos^{2} θ - 1) + \frac{M_{S}}{2 M_{T}} {(\frac{R}{r_{S}})}^{3} R (3 \cos^{2} θ - 1)$

La máxima diferencia de nivel entre la marea baja y pleamar es de 53.4+24.4=77.8 cm. Cuando los dos cuerpos celestes están en conjunción alineados con la Tierra se producen la máxima elevación y cuando están en cuadratura se producen la mínima elevación.

Rotación de la Tierra

Ahora bien, esta no es la situación real. La Tierra se mueve respecto de su eje con un periodo de 24 h 22 min. Su velocidad angular de rotación es ω=2π/P.

La elevación en función de la latitud

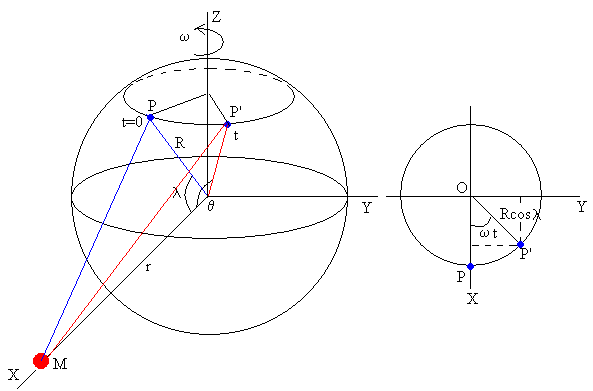
Supongamos que en el instante t=0, el punto P sobre la superficie de la Tierra a una latitud λ, y el cuerpo perturbador M están en el plano XZ. Al cabo de un cierto tiempo t, debido a la rotación de la Tierra, el punto P se habrá desplazado a la posición P’.

El ángulo θ, formado la recta que une el centro de la Tierra con el punto P' y el centro de la Tierra con el centro del cuerpo perturbador o bien, por el vector $\vec{R}$ y el vector $\vec{r}$ , se puede calcular por medio del producto escalar.

$\begin{array}{l} \vec{r} = r \hat{i} \\ \vec{R} = R \cos λ \cos (ω t) \hat{i} + R \cos λ \sin (ω t) \hat{j} + R \sin λ \hat{k} \end{array}$

El producto escalar vale

$\begin{array}{l} \vec{r} \cdot \vec{R} = R \cdot r \cos θ = R \cdot r \cos λ \cos (ω t) \\ \cos θ = \cos λ \cos (ω t) \end{array}$

La elevación en función de la latitud y el ángulo de declinación

Si el cuerpo perturbador no está en el plano ecuatorial, sino que forma un ángulo δ, de declinación con dicho plano.

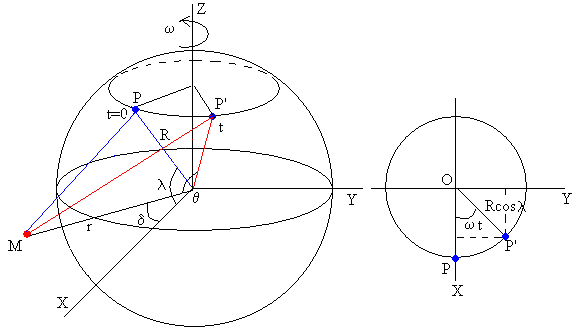
El vector se escribe ahora

$\vec{r} = r \cos δ \hat{i} + r \sin δ \hat{k}$

El producto escalar vale

$\begin{array}{l} \vec{r} \cdot \vec{R} = R \cdot r \cos θ = R \cdot r \cos λ \cos (ω t) \cos δ + R \cdot r \sin λ \sin δ \\ \cos θ = \cos λ \cos (ω t) \cos δ + \sin λ \sin δ \end{array}$

Finalmente, si P no parte del plano XZ (meridiano de Greenwich) sino de una meridiano inicial φ. La fórmula se convierte en

cosθ=cosλ cos(ωt+φ) cosδ+sinλ sinδ

Introduciendo cosθ en la expresión de la elevación del agua, y teniendo en cuenta las identidades trigonométricas cos2β=2cos²β-1,sin²β+cos²β=1, sin2β =2sinβcosβ, se llega al siguiente resultado.

$h = \frac{M R^{4}}{2 M_{T} r^{3}} (\begin{array}{l} \frac{3}{2} sin 2 δ \cdot sin 2 λ \cos (ω t + ϕ) + \\ \frac{3}{2} \cos^{2} δ \cos^{2} λ \cos (2 ω t + 2 ϕ) + \\ \frac{1}{2} (3 {sin}^{2} λ - 1) (3 {sin}^{2} δ - 1) \end{array})$

El primer sumando, depende armónicamente de ωt y completa un periodo de oscilación cuando ωt=2π, es decir, cuando la Tierra da una vuelta completa. Estas son las mareas diurnas, lunares o solares según que M y r sean, respectivamente, los datos de la masa de la Luna y su distancia al centro del la Tierra o los datos relativos al Sol.

En el ecuador estas mareas desaparecen ya que la latitud λ=0. En cambio, se hacen grandes para latitudes de λ=45º.

El segundo sumando, depende armónicamente de 2ωt, por tanto, cada 12 horas se produce un ciclo de marea. Su amplitud se hace nula en los polos λ=90º y son máximas en el ecuador λ=0º.
El tercer sumando, no depende del tiempo y se anula para aquellas latitudes tales que sin²λ=1/3, λ≈35º, y tiene su máximo valor en los polos. Finalmente, depende del ángulo de declinación δ que a su vez depende del movimiento de la Luna y del Sol.

Oscilaciones forzadas

La descripción de las mareas que se ha hecho en los apartados anteriores corresponde al efecto de la Luna y del Sol sobre una capa de agua de espesor uniforme que cubre la Tierra por completo. La Tierra está cubierta de agua en sus tres cuartas partes y su distribución no es uniforme, tanto en profundidad como en extensión. Tenemos grandes océanos, mares cerrados como el Mediterráneo, lagos, bahías, etc. La diferencia de nivel entre la marea baja y la alta cambia de un lugar a otro, así en el mar Mediterráneo es muy pequeña y en ciertas bahías como la de Fundy en Canadá es muy grande

Resonancia

Hemos observado, que un punto de la superficie líquida de la Tierra está sometido a una fuerza oscilante, cuyo periodo es de 12 horas aproximadamente y cuya amplitud es variable. Una bahía es una cavidad con determinados modos de oscilación, que dependen de su forma, extensión y profundidad de sus aguas. En ciertos lugares como Mont St Michel en la Bretaña francesa o la bahía de Fundy en Canadá se pueden producir situaciones de resonancia, con una diferencia de altura entre el flujo y el reflujo que van desde los 15 metros en la localidad francesa a 20 m en la bahía de Canadá.

Efecto sobre la rotación de los cuerpos

El efecto de las mareas es una disminución progresiva en la velocidad de rotación de la Tierra. La duración del día se incrementa en 3.5 milisegundos por cada siglo.

Si consideramos que la Luna tuvo alguna vez en su historia remota una parte fluida, los efectos de marea provocados por la acción de la Tierra fueron enormes. Se puede hacer un cálculo y mostrar que estos son 6000 veces mayores que los que produce la Luna en la Tierra. El efecto de estas intensísimas mareas explica el hecho de que siempre vemos la misma cara de la Luna.

Venus que está mucho más cerca del Sol, tiene una baja velocidad de rotación, la duración de un día venusiano es de 243.16 días terrestres, el año venusiano consta aproximadamente de dos días solares.

No se pueden explicar ciertos movimientos de planetas y satélites sin recurrir al mecanismo de fricción de marea.

Actividades

Sistema inmóvil Tierra -Luna o Tierra – Sol.

Comparamos los "efectos de marea" sobre la Tierra producidos separadamente por la Luna y por el Sol. Se supone que la Luna y el Sol están a una distancia fija de la Tierra, en su plano ecuatorial y que ésta no tiene movimiento de rotación.

Se activa el botón titulado Luna,
Se pulsa el botón titulado Nuevo

Si se activa la casilla titulada Fuerzas, se observa las componentes tangencial y radial de las fuerza de marea que se ejercen en varios puntos de la superficie terrestre.

Se activa el botón titulado Sol,
Se pulsa el botón titulado Nuevo

La superficie de agua se desvía de la forma esférica y esta desviación como puede apreciarse, no está realizada a escala.

De la representación gráfica sacamos las siguientes conclusiones

Los valores máximos (positivos) apareen en la zona de la superficie de la Tierra más cercana a la Luna (θ =0º) y en la zona más alejada (θ =180º). En estas zonas los cuerpos pesan menos, la superficie del agua se eleva.
Los valores mínimos (negativos) se producen en las zonas intermedias (θ =90º) y (θ =270º), en estas zonas los cuerpos pesan más, la superficie del agua se hunde.
Fijarse que la interacción gravitatoria disminuye con el cuadrado de la distancia a pesar de la enorme masa del Sol sus efectos sobre el nivel de las aguas es mucho menor que la producida por la Luna. El efecto del Sol es algo menos de la mitad que el producido por la Luna.

Fuerza marea

La Tierra gira alrededor de su eje, la Luna da vueltas en torno a la Tierra.

Examinamos la altura de la marea en un punto situado en el plano ecuatorial a medida que transcurre el tiempo, en dos situaciones independientes:

La Luna y la Tierra están en posiciones fijas, pero la Tierra describe un movimiento de rotación en torno a su eje, a razón de una vuelta por día.
La Tierra gira sobre su eje y la Luna describe una órbita circular alrededor de la Tierra con un periodo de 27.32 días.

Se activa el botón de radio titulado Gira la Tierra
Se pulsa el botón titulado Empieza
Se activa el botón de radio titulado Se mueven los dos cuerpos
Se pulsa el botón titulado Empieza

Suponiendo que la Luna estuviese fija, debido a la rotación de la Tierra, al cabo de seis horas un punto que estuviese en θ=0º o en θ=180º (marea alta) pasará a la posición θ=90º o θ=270º (marea baja). Seis horas más tarde se invertirá la situación y así sucesivamente. Por tanto, en un punto del plano ecuatorial de la Tierra se producirán dos pleamares y dos bajamares. El "efecto de la marea" producido por la Luna cuando consideramos únicamente el movimiento de rotación de la Tierra es la oscilación de un punto de la superficie líquida con un periodo P₀=24/2=12 horas.

Finalmente, consideramos el efecto conjunto de ambos movimientos. El "efecto de marea" producido por la Luna en un punto de la superficie líquida cuando consideramos el efecto simultáneo de los dos movimientos es un cambio en el intervalo de tiempo entre dos pleamares o dos bajamares. Si el movimiento de la Luna y la rotación de la Tierra tienen el mismo sentido. El nuevo periodo vendrá dado por

$P = \frac{π}{ω_{T} - ω_{L}} = 12.46 h$

La velocidad angular de la Tierra es 1 vuelta cada día, la de la Luna es una vuelta cada 27.32 días.

Efecto de la Luna y del Sol

Examinamos el efecto por separado y conjunto la Luna y el Sol sobre las mareas en la Tierra.

Activamos el primer botón de radio titulado efecto de la Luna y volvemos a examinar el efecto únicamente de la Luna sobre las mareas, que ya hemos descrito en el apartado anterior.

Activamos el segundo botón de radio y observamos el efecto del Sol sobre las mareas. Se ha supuesto que el centro de la Tierra describe una órbita circular alrededor del Sol con un periodo de 365 días.

En el primer apartado, vimos que el efecto del Sol era mucho menor que el de la Luna, la posición de la Tierra cambia muy poco durante un día, por lo que las mareas debidas al Sol tienen un periodo de prácticamente 12 horas pero su amplitud es algo menos de la mitad que las producidas por la Luna. Después de muchos días, empieza a ser apreciable el cambio de la hora en la que se produce la pleamar o la bajamar debida exclusivamente al movimiento de la Tierra en órbita circular alrededor del Sol.

Activando el botón de radio Efecto de ambos, observamos el efecto debido a la Luna y al Sol. Aunque el efecto dominante es el de la Luna, el comportamiento es muy complejo. Pero caben destacar dos rasgos:

Cuando la Luna y el Sol están alineados con la Tierra el efecto de la marea es muy intenso, esta situación se denomina "marea viva", que a su vez corresponde a las fases lunares luna nueva y luna llena.

Cuando la Luna y el Sol está en cuadratura, es decir, cuando la línea que une el Sol con La Tierra hace 90º con la línea que une la Tierra y la Luna, los efectos se contraponen dando lugar a las denominadas "mareas muertas", que corresponden a las fases lunares de cuarto creciente y cuarto menguante.

Hemos presentado un modelo simple, que permite explicar cualitativamente las mareas. Pero la realidad es mucho más compleja. La Tierra no es homogénea, no es una esfera perfecta y la rotación hace que el valor de la aceleración de la gravedad y su dirección cambien ligeramente con la latitud, siendo mínima en el Ecuador y máxima en los polos. Las órbitas de la Luna alrededor de la Tierra y de la Tierra alrededor del Sol no son circunferencias sino elipses de pequeña excentricidad.

En los mares pequeños como el Mediterráneo el efecto de las mareas es relativamente pequeño. Sin embargo, las mareas son mucho más intensas en las costas de los grandes océanos.

Nota: El tamaño de la órbita de la Luna alrededor de la Tierra está muy exagerado, ya que la razón del radio r de la órbita de la Luna, al radio medio R de la órbita de la Tierra alrededor del Sol es, r/R=0.0026

Deformación de la capa de agua que rodea a la Tierra

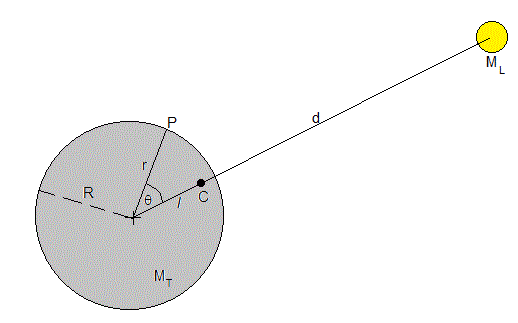
Se utilizan coordenadas polares (r,θ) para determinar el estado de un punto P cercano a la superficie de la Tierra tomando como referencia (eje X) la recta que une el centro de la Tierra y de la Luna cuyos centros distan d. C es la posición del centro de masas del sistema de dos partículas, la distancia entre el centro de la Tierra y el centro de masas es $l = \frac{M_{L} d}{M_{L} + M_{T}}$ . Finalmente, R es el radio de la Tierra

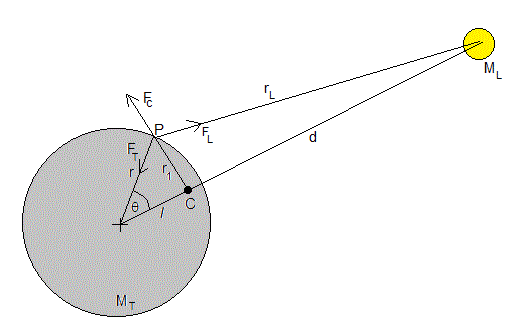
Las fuerzas que actúan sobre una partícula de masa m situada en P son:

la fuerza de atracción de la Tierra
La fuerza de atracción de la Luna
La fuerza centrífuga (describimos el movimiento en un sistema de referencia no inercial)

Las tres fuerzas dependen de la posición del punto P.

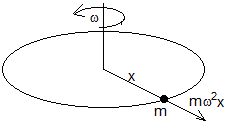
La fuerza centrífuga es proporcional al radio x de la circunferencia que describe la partícula de masa m

Calculamos la energía potencial correspondiente a esta fuerza, sabiendo que el trabajo de una fuerza conservativa es igual a la diferencia entre el valor inicial y el valor final de una función E_p(x) que solamente depende del radio x

$\begin{array}{l} \int_{1}^{2} (m ω^{2} x) d x = (- \frac{1}{2} m ω^{2} x_{1}^{2}) - (- \frac{1}{2} m ω^{2} x_{2}^{2}) \\ E_{p} (x) = - \frac{1}{2} m ω^{2} x^{2} \end{array}$

Hemos demostrado en páginas anteriores, que la energía potencial correspondiente a la fuerza de atracción GMm/r² es -GMm/r

La energía potencial E_p de una partícula de masa m situada en el punto P cercano a la superficie de la Tierra se compone de la suma de tres términos:

$E_{p} (r, θ) = - G \frac{M_{L} m}{r_{L}} - G \frac{M_{T} m}{r} - \frac{1}{2} m ω^{2} r_{1}^{2}$

Relacionamos r_L y r₁ con r y θ

$\begin{array}{l} r_{L}^{2} = r^{2} + d^{2} - 2 r d \cos θ \\ r_{1}^{2} = r^{2} + l^{2} - 2 r l \cos θ \end{array}$

El radio r es pequeño en comparación con la distancia d entre el centro de la Tierra y la Luna

Como el cociente x=r/d es pequeño, hacemos la siguiente aproximación

$\frac{1}{r_{L}} = \frac{1}{d \sqrt{1 + x^{2} - 2 x \cos θ}} \approx \frac{1}{d} (1 + x \cos θ + \frac{1}{2} x^{2} (3 \cos^{2} θ - 1))$

syms a x; %a es cosθ
>> taylor(1/sqrt(1+x^2-2*a*x),x,0,'order',3)
ans =((3*a^2)/2 - 1/2)*x^2 + a*x + 1

Teniendo en cuenta que la partícula de masa reducida μ describe un movimiento circular uniforme de radio d con velocidad angular ω. La energía potencial por unidad de masa m, E_p/m se escribe

$\frac{E_{p} (r, θ)}{m} = - G \frac{M_{L}}{d} (1 + \frac{r}{d} \cos θ + \frac{1}{2} {\frac{r}{d^{2}}}^{2} (3 \cos^{2} θ - 1)) - G \frac{M_{T}}{r} - \frac{1}{2} G \frac{(M_{L} + M_{T})}{d^{3}} (r^{2} + l^{2} - 2 r l \cos θ)$

Eliminamos los términos constantes, ya que la energía potencial está definida salvo una constante aditiva, que es la que nos sirve para establecer el nivel cero de energía potencial

$\frac{E'_{p} (r, θ)}{m} = - G \frac{M_{L}}{d} (\frac{r}{d} \cos θ + \frac{1}{2} \frac{r^{2}}{d^{2}} (3 \cos^{2} θ - 1)) - G \frac{M_{T}}{r} - \frac{1}{2} G \frac{(M_{L} + M_{T})}{d^{3}} (r^{2} - 2 r \frac{M_{L} d}{M_{L} + M_{T}} \cos θ)$

Simplificando

$\frac{E'_{p} (r, θ)}{m} = - G M_{L} \frac{1}{2} \frac{r^{2}}{d^{3}} (3 \cos^{2} θ - 1) - G M_{T} \frac{1}{r} - \frac{1}{2} G (M_{L} + M_{T}) \frac{r^{2}}{d^{3}}$

El punto P está en las proximidades de la superficie de la Tierra

La última aproximación, consiste en suponer que el punto P está muy cerca de la superficie de la Tierra, de modo que r=R+h, siendo R el radio de la Tierra y h la altura de la deformación de la capa esférica uniforme de agua que rodea a la Tierra, h<<R. Hacemos las siguientes aproximación:

$\frac{1}{r} = \frac{1}{R + h} = \frac{1}{R} {(1 + \frac{h}{R})}^{- 1} \approx \frac{1}{R} (1 - \frac{h}{R})$

La expresión de la energía potencial, después de eliminar los términos constantes se reduce a

$\frac{E'_{p} (r, θ)}{m} = - G M_{L} \frac{1}{2} \frac{r^{2}}{d^{3}} (3 \cos^{2} θ - 1) - G M_{T} \frac{1}{R} + G M_{T} \frac{h}{R^{2}} - \frac{1}{2} G (M_{L} + M_{T}) \frac{r^{2}}{d^{3}}$

Como r²≈R²+2Rh. Pero Rh/d³ es muy pequeño, ya que h<<R y R<<d

$\frac{E''_{p} (r, θ)}{m} = - G M_{L} \frac{1}{2} \frac{R^{2}}{d^{3}} (3 \cos^{2} θ - 1) + G M_{T} \frac{h}{R^{2}}$

Dado que la superficie de la capa de agua es una superficie equipotencial, E_p(r,θ) tiene que tener el mismo valor en todos los puntos P de dicha superficie. Se deberá de cumplir que

$\begin{array}{l} G M_{T} \frac{h}{R^{2}} = G M_{L} \frac{1}{2} \frac{R^{2}}{d^{3}} (3 \cos^{2} θ - 1) \\ h = \frac{1}{2} (\frac{M_{L}}{M_{T}}) R {(\frac{R}{d})}^{3} (3 \cos^{2} θ - 1) \end{array}$

h es la altura de la deformación de la capa esférica uniforme de agua que rodea a la Tierra

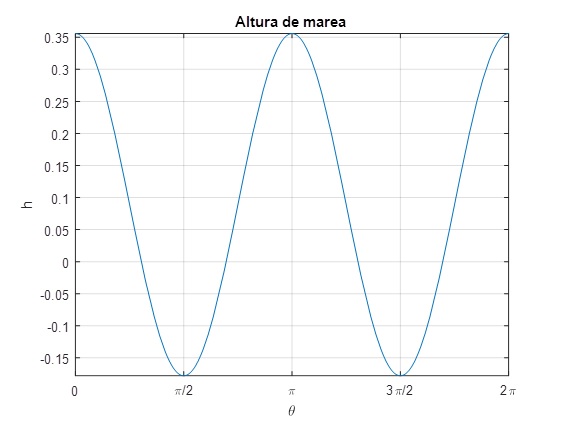
Los valores más grandes de h se producen para θ=0 y θ=π en la dirección que une la Luna y y la Tierra

$h_{m á x} = (\frac{M_{L}}{M_{T}}) R {(\frac{R}{d})}^{3}$

Mientras que los valores más pequeños se producen para θ=π/2 y 3π/2, en la dirección perpendicular a la recta que une el centro de la Tierra y de la Luna

$h_{m í n} = - \frac{1}{2} (\frac{M_{L}}{M_{T}}) R {(\frac{R}{d})}^{3}$

La diferencia de alturas es

$Δ h = h_{m á x} - h_{m í n} = \frac{3}{2} (\frac{M_{L}}{M_{T}}) R {(\frac{R}{d})}^{3} = 0.5337 m$

G=6.67*10^-11;
d=384.4*10^6;
MT=5.98*10^24;
ML=7.34*10^22;
R=6.37*10^6;
h=@(x) ML*R^4*(3*cos(x).^2-1)/(2*MT*d^3);
fplot(h,[0,2*pi])
set(gca,'XTick',0:pi/2:2*pi)
set(gca,'XTickLabel',{'0','\pi/2','\pi','3\pi/2','2\pi'})
grid on
xlabel('\theta')
ylabel('h')
title('Altura de marea')

Referencias

Kapoulitsas G. On the generation of tides. Eur. J. Phys. 6 (1985) pp. 201-207

Butikov E. A dynamical picture of the oceanic tides. Am. J. Phys. 70 (10) October 2002, pp. 1001-1011

Ultimo apartado

Problema de la XXVII Olimpiada Internacional de Física. Oslo, 1996