Trayectorias elípticas con el eje girado
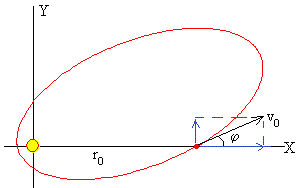
En este apartado, vamos a determinar la ecuación de la elipse que describe una partícula que dista r0 del centro de fuerzas, disparada con velocidad inicial v0, haciendo un ángulo φ entre dicha velocidad y la línea que une el centro fuerzas y el punto de disparo, tal como se muestra en la figura.
Fuerza central y conservativa
Por ser la fuerza de atracción conservativa, la energía es constante en todos los puntos de la trayectoria y vale
Por ser la fuerza de atracción central, el momento angular es constante en todos los puntos de la trayectoria.
L=mr0·v0·sinφ
En la página, Ecuación de la trayectoria, obtuvimos
r y θ son las coordenadas polares de la partícula y ε<1 es la excentricidad de la elipse.
Para θ=0, la distancia de la partícula al centro de fuerzas es r=r0. Obtenemos el valor de θ0
Conocida la energía E y del momento angular L, determinamos los valores de los parámetros d y ε de la elipse.
Definimos el parámetro adimensional
cociente entre la energía potencial y la cinética en la posición de partida. Para una trayectoria parabólica
p=1. Para una trayectoria elíptica, E<0, p>1
En función de este parámetro
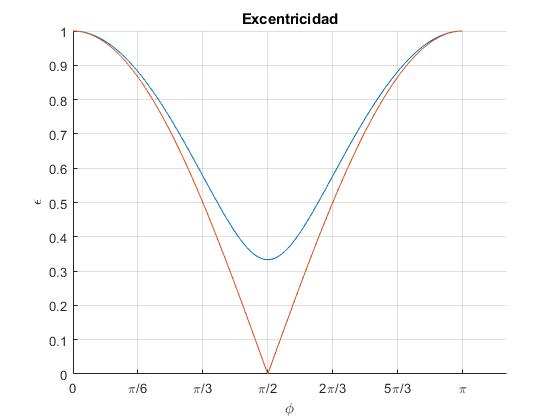
A medida que el ángulo de disparo cambia, 0<φ<π, la excentricidad de la elipse varía
-
La excentricidad es máxima ε=1, cuando φ=0
-
La excentricidad es mínima ε=(p-2)/p, cuando φ=π/2
Como caso particular mencionaremos, que cuando p=2, o cuando la velocidad de disparo es
la trayectoria es una circunferencia, ε=0, de radio r0.
e=@(p, x) sqrt(1-(p-1)*(2*sin(x)/p).^2);
hold on
fplot(@(x) e(1.5,x),[0,pi])
fplot(@(x) e(2,x),[0,pi])
hold off
set(gca,'XTick',0:pi/6:pi)
set(gca,'XTickLabel',{'0','\pi/6','\pi/3','\pi/2','2\pi/3', '5\pi/3','\pi'})
grid on
xlabel('\phi')
ylabel('\epsilon');
title('Excentricidad')
Introducimos los valores de θ0, excentricidad ε y parámetro d en términos de r0, p y ángulo φ en la ecuación de la elipse.
Simplificando, llegamos a la ecuación
La ecuación de la trayectoria depende del ángulo φ con el que se dispara la partícula.
f(r, θ, φ)=0
Ecuación del movimiento
Al integrar las ecuaciones del movimiento de una partícula bajo la acción de una fuerza inversamente proporcional al cuadrado de la distancia r al centro de fuerzas, obtuvimos
Derivamos respecto del tiempo y teniendo en cuenta la expresión del momento angular en coordenadas polares, L=mr2(dθ/dt)
Los coeficientes A y B se determinan a partir de las condiciones iniciales: θ=0, r=r0 y las componentes de la velocidad v0 son:
Los coeficientes A y B valen:
Obtenemos la misma ecuación de la elipse en términos del parámetro adimensional p
r0=3; %posición inicial
phi=pi/6; %ángulo de tiro
p=1.5; %parámetro adimensional
r=@(x) r0./(-cos(phi)*sin(x)/sin(phi)+cos(x)+p*(1-cos(x))/(2*sin(phi)^2));
theta=(0:360)*pi/180;
hold on
%origen, centro de fuerzas
plot(0,0,'ro', 'markersize',8,'markerfacecolor','y')
%punto de lanzamiento
plot(r0,0,'ko', 'markersize',4,'markerfacecolor','k')
%vector velocidad inicial
quiver(r0,0, sqrt(2/p)*cos(phi), sqrt(2/p)*sin(phi))
%trayectoria
plot(r(theta).*cos(theta),r(theta).*sin(theta),'r')
%eje mayor de la elipse girada
d=2*r0*sin(phi)^2/p;
e=sqrt(1-(p-1)*(2*sin(phi)/p)^2);
phi_0=-acos((d-r0)/(r0*e));
x1=r(phi_0)*cos(phi_0);
y1=r(phi_0)*sin(phi_0);
x2=r(phi_0+pi)*cos(phi_0+pi);
y2=r(phi_0+pi)*sin(phi_0+pi);
line([x1,x2],[y1,y2])
hold off
grid on
xlabel('x')
ylabel('y')
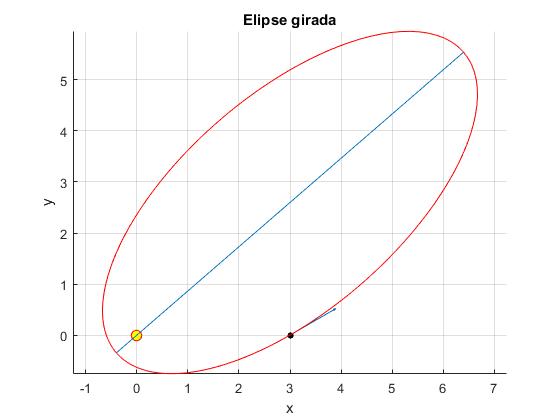
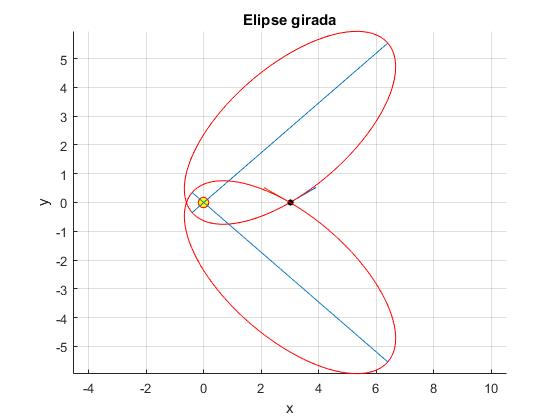
title('Elipse girada')
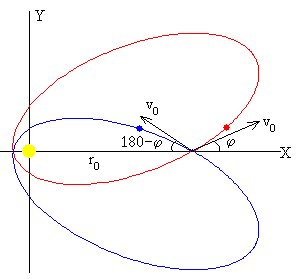
Las elipses correspondientes a dos ángulos de tiro suplementarios φ y 180-φ, tienen el mismo momento angular L y la misma energía E, son simétricas con respecto del eje X
r0=3; %posición inicial
p=1.5; %parámetro adimensional
phi=pi/6; %ángulo de tiro
r=@(x) r0./(-cos(phi)*sin(x)/sin(phi)+cos(x)+p*(1-cos(x))/(2*sin(phi)^2));
theta=(0:360)*pi/180;
hold on
%origen, centro de fuerzas
plot(0,0,'ro', 'markersize',8,'markerfacecolor','y')
%punto de lanzamiento
plot(r0,0,'ko', 'markersize',4,'markerfacecolor','k')
%vector velocidad inicial
quiver(r0,0, sqrt(2/p)*cos(phi), sqrt(2/p)*sin(phi))
%trayectoria
plot(r(theta).*cos(theta),r(theta).*sin(theta), 'r')
%eje mayor de la elipse girada
d=2*r0*sin(phi)^2/p;
e=sqrt(1-(p-1)*(2*sin(phi)/p)^2);
phi_0=-acos((d-r0)/(r0*e));
x1=r(phi_0)*cos(phi_0);
y1=r(phi_0)*sin(phi_0);
x2=r(phi_0+pi)*cos(phi_0+pi);
y2=r(phi_0+pi)*sin(phi_0+pi);
line([x1,x2],[y1,y2])
phi=pi-pi/6; %ángulo de tiro
r=@(x) r0./(-cos(phi)*sin(x)/sin(phi)+cos(x)+p*(1-cos(x))/(2*sin(phi)^2));
theta=(0:360)*pi/180;
%punto de lanzamiento
plot(r0,0,'ko', 'markersize',4,'markerfacecolor','k')
%vector velocidad inicial
quiver(r0,0, sqrt(2/p)*cos(phi), sqrt(2/p)*sin(phi))
%trayectoria
plot(r(theta).*cos(theta),r(theta).*sin(theta), 'r')
%eje mayor de la elipse girada
d=2*r0*sin(phi)^2/p;
e=sqrt(1-(p-1)*(2*sin(phi)/p)^2);
phi_0=acos((d-r0)/(r0*e));
x1=r(phi_0)*cos(phi_0);
y1=r(phi_0)*sin(phi_0);
x2=r(phi_0+pi)*cos(phi_0+pi);
y2=r(phi_0+pi)*sin(phi_0+pi);
line([x1,x2],[y1,y2])
hold off
axis equal
grid on
xlabel('x')
ylabel('y')
title('Elipse girada')
Trayectorias que pasan por dos puntos
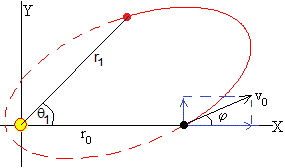
En el tiro parabólico estudiamos un ejemplo similar, calcular los dos ángulos de tiro de un proyectil para que impacte en un blanco dado.
Desde la posición r0, θ=0, se disparan proyectiles con velocidad v0 y ángulo de tiro φ. La posición del blanco es r1, θ1.
La ecuación de la trayectoria que parte de la posición de disparo es
Conocido el ángulo de tiro φ, despejamos del parámetro p (velocidad de disparo v0)
- Posición de disparo, r0=3
- Angulo de tiro, φ=π/6 (30°)
- Posición del blanco, r1=10, θ1=π/4 (45°)
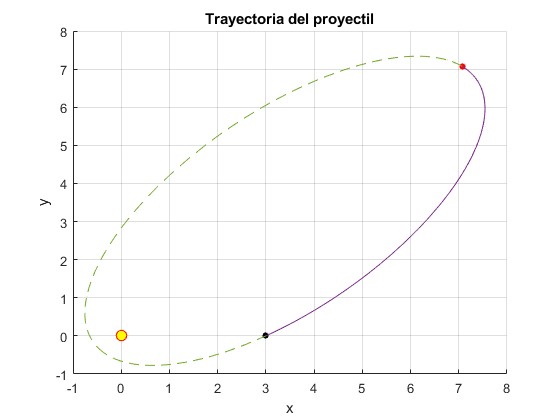
La trayectoria pasa por la posición del blanco.
Ejemplo
r0=3; %posición disparo
phi=pi/6; %ángulo de tiro
r1=10; %posición del blanco
th_1=45*pi/180;
p=2*(r0/r1+cos(phi)*sin(th_1)/sin(phi)-cos(th_1))*sin(phi)^2/(1-cos(th_1));
hold on
%origen, centro de fuerzas
plot(0,0,'ro', 'markersize',8,'markerfacecolor','y')
%posición de disparo
plot(r0,0,'ko', 'markersize',4,'markerfacecolor','k')
%posición del blanco
plot(r1*cos(th_1),r1*sin(th_1),'ro', 'markersize',4,'markerfacecolor','r')
%trayectoria
r=@(x) r0./(-cos(phi)*sin(x)/sin(phi)+cos(x)+p*(1-cos(x))/(2*sin(phi)^2));
fplot(@(x) r(x).*cos(x),@(x) r(x).*sin(x),[0,th_1])
fplot(@(x) r(x).*cos(x),@(x) r(x).*sin(x),[th_1,2*pi],'lineStyle','--')
hold off
grid on
xlabel('x')
ylabel('y')
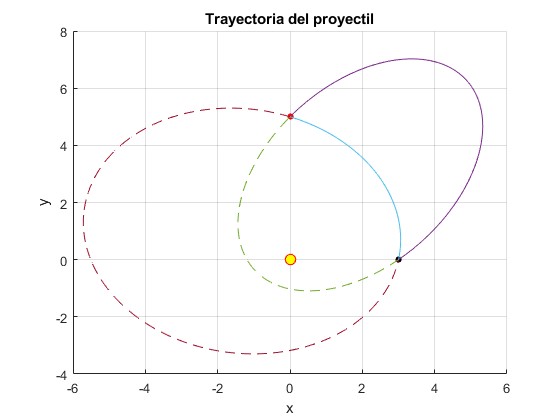
title('Trayectoria del proyectil')
p = 1.3958
A partir del valor del parámetro p determinamos la velocidad v0 de disparo
Fijado el valor del parámetro p vamos a calcular el ángulo o los ángulos de tiro φ que hacen que el proyectil impacte en el blanco
Obtenemos una ecuación transcendente en φ que estudiaremos más abajo
- Posición de disparo, r0=3
- Parámetro, p=1.5
- Posición del blanco, r1=5, θ1=π/2 (90°)
r0=3; %posición de disparo
p=1.5; %parámetro adimensional
r1=5; %posición del blanco
th_1=90*pi/180;
f=@(x) sin(th_1)*sin(2*x)-(r0/r1-cos(th_1))*cos(2*x)-p+r0/r1+(p-1)*cos(th_1);
fplot(f,[0,pi])
phi_1=fzero(f,[0,1]);
phi_2=fzero(f,[1,pi]);
grid on
xlabel('x')
ylabel('y')
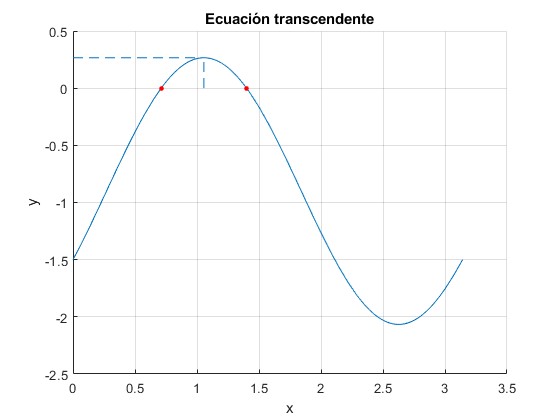
title('Ecuación transcendente')
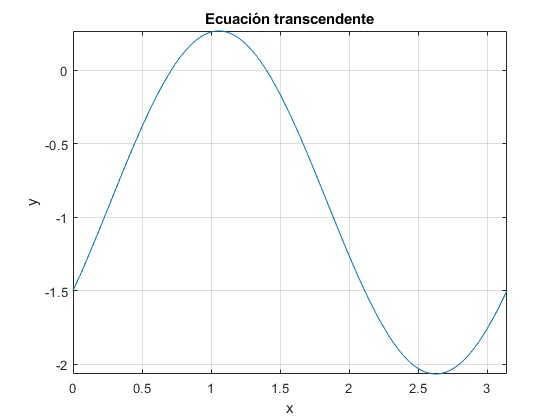
La ecuación transcedente tiene dos raíces, que corresponden a dos ángulos de tiro φ1=40.7 y φ1=80.2°
phi_1 = 0.7110 phi_2 = 1.4002
Representamos las trayectorias que unen los dos puntos
r0=3; %posición disparo
p=1.5; %parámetro adimensional
r1=5; %posición blanco
th_1=90*pi/180;
f=@(x) sin(th_1)*sin(2*x)-(r0/r1-cos(th_1))*cos(2*x)-p+r0/r1+(p-1)*cos(th_1);
phi_1=fzero(f,[0,1]); %ángulos de tiro
phi_2=fzero(f,[1,pi]);
hold on
%origen, centro de fuerzas
plot(0,0,'ro', 'markersize',8,'markerfacecolor','y')
%posición disparo
plot(r0,0,'ko', 'markersize',4,'markerfacecolor','k')
%posición blanco
plot(r1*cos(th_1),r1*sin(th_1),'ro', 'markersize',4,'markerfacecolor','r')
%trayectorias
r=@(x) r0./(-cos(phi_1)*sin(x)/sin(phi_1)+cos(x)+p*(1-cos(x))/(2*sin(phi_1)^2));
fplot(@(x) r(x).*cos(x),@(x) r(x).*sin(x),[0,th_1])
fplot(@(x) r(x).*cos(x),@(x) r(x).*sin(x),[th_1,2*pi],'lineStyle','--')
r=@(x) r0./(-cos(phi_2)*sin(x)/sin(phi_2)+cos(x)+p*(1-cos(x))/(2*sin(phi_2)^2));
fplot(@(x) r(x).*cos(x),@(x) r(x).*sin(x),[0,th_1])
fplot(@(x) r(x).*cos(x),@(x) r(x).*sin(x),[th_1,2*pi],'lineStyle','--')
hold off
grid on
xlabel('x')
ylabel('y')
title('Trayectorias del proyectil')
La ecuación transcendente
Calculamos el máximo φm de la ecuación transcendente
Calculamos ym=f(φm)
ym tendrá que ser mayor que cero para que existan dos raíces, dos ángulos de tiro
Lo que implica que el parámetro p tiene que ser menor que pm
r0=3; %posición de disparo
p=1.5; %parámetro adimensional
r1=5; %posición del blanco
th_1=90*pi/180;
f=@(x) sin(th_1)*sin(2*x)-(r0/r1-cos(th_1))*cos(2*x)-p+r0/r1+(p-1)*cos(th_1);
hold on
fplot(f,[0,pi])
%máximo
phi_m=atan(sin(th_1)/(cos(th_1)-r0/r1))/2+pi/2;
ym=sqrt(1+(r0/r1)^2-2*r0*cos(th_1)/r1)+r0/r1-cos(th_1)-p*(1-cos(th_1));
line([phi_m,phi_m], [0, ym], 'lineStyle','--')
line([0,phi_m], [ym, ym], 'lineStyle','--')
%raíces
phi_1=fzero(f,[0,phi_m]);
phi_2=fzero(f,[phi_m,pi]);
plot(phi_1,0,'ro','markersize',3,'markerfacecolor','r')
plot(phi_2,0,'ro','markersize',3,'markerfacecolor','r')
p_m=(r0/r1-cos(th_1)+sqrt(1+(r0/r1)^2-2*r0*cos(th_1)/r1))/(1-cos(th_1));
hold off
grid on
xlabel('x')
ylabel('y')
title('Ecuación transcendente')
>> p_m p_m = 1.7662
El valor de pm que hace ym=0. Para que existan dos raíces (señaladas por dos puntos de color rojo), se tiene que cumplir que p<pm
Orbitas de la misma energía
Imaginemos un misil lanzado desde la superficie de la Tierra verticalmente y que en el punto más alto de su trayectoria explota en varios fragmentos iguales que salen en todas las direcciones con igual velocidad.
El movimiento posterior de los fragmentos, se debe únicamente a la fuerza de atracción de la Tierra y por tanto, describirán órbitas elípticas si su energía total es negativa.
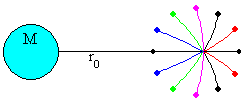
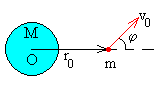
El momento angular y la energía de un fragmento de masa m lanzado desde una distancia r0 del centro de la Tierra, con velocidad v0 haciendo un ángulo φ con el radio vector es
Todos los fragmentos tienen la misma energía E, pero distinto momento angular L
El semieje mayor a es independiente del momento angular L y solamente depende de la energía total E.
Todos los fragmentos tienen el mismo semieje mayor a. Por la tercera ley de Kepler el periodo de todos los fragmentos será el mismo. Todos los fragmentos salen a la vez del mismo punto y regresan después de un tiempo igual al periodo al mismo punto.
Vamos a estudiar ahora los distintos casos que pueden presentarse dependiendo del ángulo de lanzamiento.
Cuando el ángulo φ=0
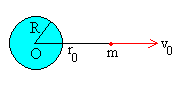
El momento angular L=0, por lo que la trayectoria es una línea recta que pasa por el centro de fuerzas. El fragmento se eleva y luego cae hacia la Tierra a lo largo de la dirección radial.
La máxima distancia r a la que se aleja el fragmento, se calcula poniendo v=0 en la ecuación de constancia de la energía y a continuación, se despeja r.
La velocidad v con la que impacta en la superficie de la Tierra, se obtiene poniendo r=R (radio de la Tierra) en la ecuación de la energía
Cuando el ángulo φ=180º
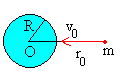
El fragmento cae directamente hacia la superficie de la Tierra, alcanzando su superficie con la velocidad v calculada en el apartado anterior.
Cuando el ángulo φ=90º
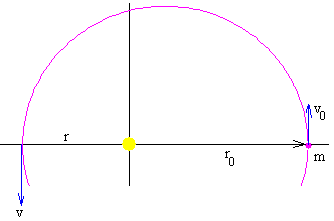
El fragmento describe una elipse cuyo eje mayor es 2a=r+r0. Aplicando la constancia del momento angular y de la energía.
Se resuelve el sistema de dos ecuaciones con dos incógnitas para calcular r y v.
Cuando el ángulo es φ
El fragmento describe una elipse cuyo eje mayor está girado con respecto del eje X.
Los dos fragmentos cuyas velocidades forman con el radio vector ángulos φ y 180-φ, tienen el mismo momento angular y la misma energía. Sus trayectorias son simétricas respecto del eje X, tal como podemos ver en la figura.
Ejemplos
Para resolver estos ejemplos se adopta un Sistema de Unidades tal que GM=1
Supongamos que introducimos los siguientes valores
-
Posición, r0=3.0
-
Velocidad, v0=0.5
Cuando el ángulo es φ=0.
La distancia máxima que alcanza el fragmento en la dirección radial es
Cuando φ=90.
Primero, calculamos la velocidad de escape a la distancia r0=3.0, que es
Después, calculamos la velocidad y la distancia máxima o mínima al centro de fuerzas
El eje mayor de la elipse es 2a= 3.0+1.8=4.8
El eje mayor de la elipse se puede obtener de forma directa mediante la fórmula
El periodo de todos los fragmentos es
Actividades
Se introduce
- La velocidad v0 del fragmento en el control titulado Velocidad
- La posición r0 en el control de edición titulado Posición.
Se pulsa el botón titulado Nuevo
No se aceptan valores de v0 y r0 que den lugar:
- a una energía E positiva o nula.
- a una trayectoria cuyo apogeo sea mayor de 6 unidades
- a una trayectoria cuyo perigeo sea menor que 0.1 unidades
En el caso de que los dos valores sean aceptados, se observa las trayectorias de los fragmentos cuya velocidad forma ángulos de 30º, 60º, 90º, 120º y 150º con el radio vector.
Observamos que todas las trayectorias tienen el mismo eje mayor y por tanto, los fragmentos se vuelven a encontrar en el punto de partida transcurrido un periodo P.
Envolvente de las trayectorias elípticas de la misma energía
Obtuvimos por dos procedimientos la ecuación de la trayectoria elíptica en términos del ángulo de disparo φ
La ecuación de la envolvente de las trayectorias elípticas se obtiene derivando la ecuación de la elipse, f(r,θ,φ)=0 con respecto a φ e igualando a cero.
y combinando ésta con la ecuación de la trayectoria f(r,θ,φ)=0 para eliminar el ángulo φ. La derivada con respecto a φ vale
Simplificando llegamos a la expresión
Introducimos esta expresión en la ecuación de la elipse, teniendo en cuenta la relación trigonométrica
realizando algunas operaciones
y despejando r, obtenemos la ecuación de la elipse
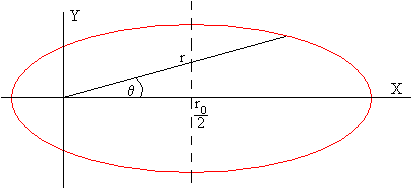
Calculamos el semieje mayor a y el semieje menor b de la elipse
La ecuación de la elipse en coordenadas rectangulares es
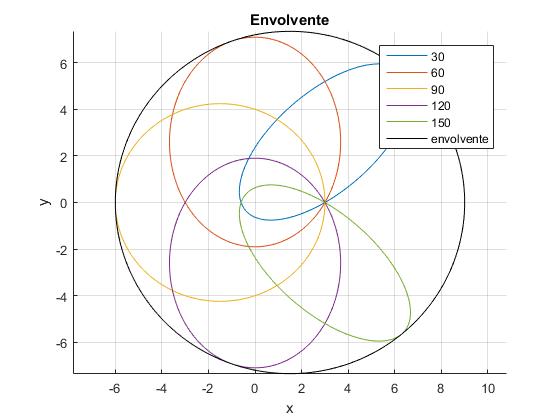
Se dibuja las trayectorias elípticas de las partículas disparadas con ángulos φ=30°, 60°, 90°, 120°, 150°. Se dibuja también la envolvente de dichas elipses.
r0=3; %posición inicial
p=1.5; %parámetro adimensional
r=@(phi,x) r0./(-cos(phi)*sin(x)/sin(phi)+cos(x)+p*(1-cos(x))/(2*sin(phi)^2));
theta=0:pi/180:2*pi;
hold on
for k=1:5
%trayectorias
plot(r(pi*k/6,theta).*cos(theta),r(pi*k/6,theta).*sin(theta)
,'displayName',num2str(k*30))
end
rEnv=@(x) 2*r0./((p-1/p)-(sqrt(p)-1/sqrt(p))^2*cos(x));
plot(rEnv(theta).*cos(theta),rEnv(theta).*sin(theta)
,'k', 'displayName','envolvente')
hold off
legend('-DynamicLegend','location','northeast')
axis equal
grid on
xlabel('x')
ylabel('y')
title('Envolvente')
Referencias
Butikov E. Families of Keplerian orbits. Eur. J. Phys. 24 (2003) pp. 175-183
Laporte O., On Kepler ellipses starting from a point of space. Am. J. Phys. 38 (7) July 1970, pp. 837-840

