Sistema aislado Tierra-Luna

En la página titulada El problema de dos cuerpos hemos estudiado el sistema aislado formado por la Tierra y la Luna

• La Tierra de masa M_T describe un movimiento circular de radio $r_T=\frac{M_L}{M_T+M_L}r$ alrededor del c.m de periodo P, tal que

${\displaystyle P^2=\frac{4{\pi }^2{r}^3}{G(M_L+M_T)},{\omega }^2=\frac{G(M_L+M_T)}{r^3}}$

• La Luna de masa M_L describe un movimiento circular de radio $r_L=\frac{M_T}{M_T+M_L}r$ alrededor del c.m y del mismo periodo o con velocidad angular ω=2π/P.

Donde r es la distancia entre el centro de la Tierra y el centro de la Luna. Los datos son

• Radio de la Tierra, R_T=6.37·10⁶ m
• Radio de la Luna, R_L=1.74·10⁶ m
• Distancia Tierra-Luna, r₀=3.84·10⁸ m, distancia inicial
• Masa de la Tierra, M_T=5.98·10²⁴ kg
• Masa de la Luna, M_L=7.34·10²² kg
• Constante G=6.67·10^-11 Nm²/kg²

Calculamos el momento angular de la Luna y de la Tierra alrededor del centro de masas

• La Luna describe una órbita circular de radio r_L con velocidad angular ω

${\displaystyle L_o=M_L{r}_L^2\omega =\text{2}.{\text{8254·10}}^{34}{\text{kgm}}^{\text{2}}\text{/s}}$

• La Luna es una esfera de radio R_L que gira alrededor de su eje con velocidad angular constante ω (velocidad angular orbital)

${\displaystyle L_s=\left(\frac{2}{5}{M}_L{R}_L^2\right)\omega =\text{2}.{\text{3658·10}}^{29}=\text{8}.{\text{3734·10}}^{-6}\text{·}{L}_o{\text{kgm}}^{\text{2}}\text{/s}}$

Este término es muy pequeño comparado con el momento angular orbital L_o y se puede despreciar. El momento angular de la Luna es L_l=2.8254·10³⁴ kgm²/s

• La Tierra describe una órbita circular de radio r_T con velocidad angular ω

${\displaystyle L_o=M_T{r}_T^2\omega =\text{3}.{\text{4722·10}}^{32}{\text{kgm}}^{\text{2}}\text{/s}}$

• LaTierra es una esfera de radio R_T que gira alrededor de su eje con velocidad angular constante Ω₀=2π/(24·60·60) rad/s

${\displaystyle L_s=\left(\frac{2}{5}{M}_T{R}_T^2\right){\Omega }_0=\text{7}.0{\text{584·10}}^{33}=\text{2}0.\text{32·}{L}_o{\text{kg·m}}^{\text{2}}\text{/s}}$

El momento angular de la Tierra es la suma de las dos contribuciones, L_t= 7.4056·10³³ kgm²/s

El momento angular total del sistema aislado Tierra-Luna es L=L_l+L_t=3.5660·10³⁴ kgm²/s

El momento angular inicial es

${\displaystyle \begin{array}{l}L=M_L{r}_L^2{\omega }_0+M_T{r}_T^2{\omega }_0+\left(\frac{2}{5}{M}_T{R}_T^2\right){\Omega }_0=\\ \left\{M_L{\left(\frac{M_T{r}_0}{M_L+M_T}\right)}^2+M_T{\left(\frac{M_L{r}_0}{M_L+M_T}\right)}^2\right\}{\omega }_0+\left(\frac{2}{5}{M}_T{R}_T^2\right){\Omega }_0=\\ \frac{M_L{M}_T}{M_L+M_T}{r}_0^2{\omega }_0+\left(\frac{2}{5}{M}_T{R}_T^2\right){\Omega }_0=\frac{M_L{M}_T{G}^{2/3}}{{\left(M_L+M_T\right)}^{1/3}}\frac{1}{{\omega }_0^{1/3}}+\left(\frac{2}{5}{M}_T{R}_T^2\right){\Omega }_0\end{array}}$

En la situación final, el periodo del movimiento orbital 2π/ω coincide con la duración del día (o periodo del movimiento de rotación de la Tierra alrededor de su eje). Aplicamos la constancia del momento angular

${\displaystyle \begin{array}{l}\frac{M_L{M}_T{G}^{2/3}}{{\left(M_L+M_T\right)}^{1/3}}\frac{1}{{\omega }^{1/3}}+\left(\frac{2}{5}{M}_T{R}_T^2\right)\omega =\frac{M_L{M}_T{G}^{2/3}}{{\left(M_L+M_T\right)}^{1/3}}\frac{1}{{\omega }_0^{1/3}}+\left(\frac{2}{5}{M}_T{R}_T^2\right){\Omega }_0\\ \frac{1}{{\omega }^{1/3}}+a\omega =\frac{1}{{\omega }_0^{1/3}}+a{\Omega }_0,a=\frac{\frac{2}{5}{M}_T{R}_T^2}{\frac{M_L{M}_T{G}^{2/3}}{{\left(M_L+M_T\right)}^{1/3}}}=\frac{2{\left(M_L+M_T\right)}^{1/3}{R}_T^2}{5M_L{G}^{2/3}}\end{array}}$

Resolvemos la ecuación en ω utilizando fzero de MATLAB

ML=7.349e22; %masa Luna
MT=5.98e24; %masa Tierra
RT=6.37e6; %radio Tierra
G=6.67e-11;
r0=384.4e6; %distancia Tierra-Luna
P=2*pi*sqrt(r0^3/(G*(ML+MT)));
w0=2*pi/P; %velocidad angular inicial de rotación
a=2*(ML+MT)^(1/3)*RT^2/(5*ML*G^(2/3));
W0=2*pi/(24*60*60); %rotación inicial de la Tierra
f=@(x) x^(-1/3)+a*x-w0^(-1/3)-a*W0;
w=fzero(f,w0);
disp(2*pi/(w*24*60*60)) %en días
r=(G*(ML+MT)/w^2)^(1/3); %distancia final Tierra-Luna
disp(r/r0)

   52.2649
    1.5427

El resultado es ω=1.3914·10^-6 rad/s, P=2π/ω=52.2649 días. r=1.5427·r₀, es la distancia final entre el centro de la Tierra y de la Luna

La Tierra se considera fija

Dado que la masa de la Tierra es considerablemente mayor que la de la Luna y que la distancia entre sus centros es mucho mayor que cualquiera de sus radios, podemos considerar la Luna como una partícula de masa M_L=7.34·10²² kg que describe una órbita circular de radio r₀=384.4·10⁶ m alrededor de la Tierra. Supondremos que el centro de masas del sistema Tierra-Luna coincide con el centro de la Tierra.

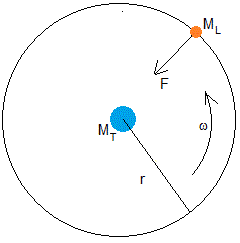
Aplicamos la dinámica del movimiento circular uniforme para describir el movimiento de la Luna alrededor de la Tierra

${\displaystyle G\frac{M_T{M}_L}{r^2}=M_L{\omega }^{2}r\omega =\sqrt{G\frac{M_T}{r^3}}}$

Consideremos que el sistema Tierra-Luna es aislado, su momento angular se mantiene constante. El momento angular se compone de dos términos:

• El de una esfera maciza (I=2M_TR²/5) de masa M_T y radio R, en movimiento de rotación alrededor de un eje fijo, con velocidad angular Ω. El momento de inercia de una esfera es I=2M_TR²/5 y el momento angular, L_T=I·Ω

• Una partícula de masa M_L que describe una movimiento circular uniforme de radio r con velocidad angular ω. El momento angular es L_L=M_Lr²ω

Consideremos el sistema Tierra-Luna en el instante inicial (figura de la izquierda) y en un instante t (figura de la derecha), cuando la velocidad angular de rotación de la Tierra alrededor de su eje fijo sea Ω y la distancia entre el centro de la Tierra y la Luna sea r.

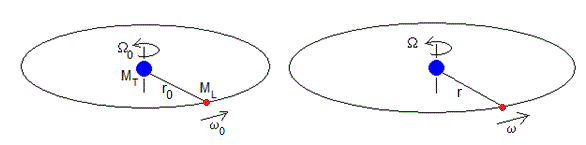
La constancia del momento angular se escribe

${\displaystyle \left(\frac{2}{5}{M}_T{R}^2\right){\Omega }_0+\left(M_L{r}_0^2\right){\omega }_0=\left(\frac{2}{5}{M}_T{R}^2\right)\Omega +\left(M_L{r}^2\right)\omega }$

Determinamos la relación entre la velocidad angular de rotación de la Tierra alrededor de su eje fijo Ω y la distancia entre el centro de la Tierra y la Luna r

${\displaystyle \begin{array}{l}\left(\frac{2}{5}{M}_T{R}^2\right){\Omega }_0+\left(M_L{r}_0^2\right)\sqrt{G\frac{M_T}{r_0^3}}=\left(\frac{2}{5}{M}_T{R}^2\right)\Omega +\left(M_L{r}^2\right)\sqrt{G\frac{M_T}{r^3}}\\ \left(\frac{2}{5}{M}_T{R}^2\right)\left({\Omega }_0-\Omega \right)=M_L\sqrt{G{M}_T}\left(\sqrt{r}-\sqrt{r_0}\right)\end{array}}$

Actualmente, la distancia entre la Tierra y la Luna es r₀=384.4·10⁶ m y la velocidad angular de rotación de la Tierra es Ω₀=2π/(24·60·60) rad/s

Suponiendo que la velocidad de alejamiento de la Luna v=0.038 m/año permanece constante, dentro de 400 millones de años la distancia Tierra-Luna habrá aumentado a r=384.4·10⁶+0.038·400·10⁶=399.6·10⁶ m

Despejamos la velocidad angular de rotación de la Tierra Ω en dicha época futura. El periodo o tiempo que tarda la Tierra en dar una vuelta sobre sí misma es P=2π/Ω

W0=2*pi/(24*3600); %velocidad angular de rotación de la Tierra
r0=384.4e6; %distancia Tierra-Luna
G=6.67e-11; %constante gravitación
MT=5.98e24; %masa de la Tierra
R=6.37e6; %radio de la Tierra
ML=7.34e22; %masa de la Luna

r=r0+0.038*400e6;
W=W0-5*sqrt(G/MT)*ML*(sqrt(r)-sqrt(r0))/(2*R^2);
P=(2*pi/W)/(60*60) %periodo de rotación de la Tierra en horas

El tiempo que tarda la Tierra en dar una vuelta sobre sí misma es (en horas)

P =   26.0792

El estado final

En el estado final, la velocidad angular de rotación Ω de la Tierra alrededor de su eje fijo se hace igual a la velocidad angular ω de la Luna en su órbita circular alrededor de la Tierra. Calculamos la distancia r entre el centro de la Tierra y la Luna

${\displaystyle \left(\frac{2}{5}{M}_T{R}^2\right){\Omega }_0+\left(M_L{r}_0^2\right)\sqrt{G\frac{M_T}{r_0^3}}=\left(\frac{2}{5}{M}_T{R}^2\right)\sqrt{G\frac{M_T}{r^3}}+\left(M_L{r}^2\right)\sqrt{G\frac{M_T}{r^3}}}$

Tenemos que resolver la ecuación en z=r/r₀ siguiente

${\displaystyle \begin{array}{l}b{z}^2+1-az\sqrt{z}=0\\ b=\frac{\left(M_L{r}_0^2\right)}{\left(\frac{2}{5}{M}_T{R}^2\right)}a=\frac{{\Omega }_0\sqrt{r_0^3}}{\sqrt{G{M}_T}}+b\end{array}}$

Para ello, utilizamos la función fzero de MATLAB

Una vez calculado r, determinamos la velocidad angular de rotación Ω de la Tierra y el tiempo que tarda en dar una vuelta completa

W0=2*pi/(24*3600); %velocidad angular de rotación de la Tierra
r0=384.4e6; %distancia Tierra-Luna
G=6.67e-11; %constante gravitación
MT=5.98e24; %masa de la Tierra
R=6.37e6; %radio de la Tierra
ML=7.34e22; %masa de la Luna

b=ML*r0^2*5/(2*MT*R^2);
a=W0*sqrt(r0^3)/sqrt(MT*G)+b;
f=@(x) b*x^2+1-a*x*sqrt(x);
z=fzero(f,[1,2])
w=sqrt(G*MT/(r0*z)^3);
P=(2*pi/w)/(3600*24)

r=1.54·r₀ y P=2π/Ω=52.4 días

z =    1.5398
P =   52.4374

Energía mínima

La Luna describe un movimiento circular de radio r alrededor del centro de la Tierra con velocidad angular ω

${\displaystyle M_L{\omega }^{2}r=G\frac{M_T{M}_L}{r^2}{r}^3=\frac{G{M}_T}{{\omega }^2}}$

El momento angular del sistema Tierra-Luna se mantiene constante e igual al momento angular actual cuando la Tierra gira alrededor de su eje con velocidad angular Ω₀=2π/(24·60·60) rad/s, y la Luna gira alrededor de la Tierra con velocidad angular

${\displaystyle {\omega }_0=\sqrt{\frac{G{M}_T}{r_0^3}}}$

con r₀=384.4·10⁶ m. Llamemos I al momento de inercia de la Tierra I=2M_TR²/5. El momento angular inicial es

${\displaystyle L=I{\Omega }_0+\left(M_L{r}_0^2\right){\omega }_0}$

El momento angular un tiempo más tarde, tiene el mismo valor

${\displaystyle L=I\Omega +\left(M_L{r}^2\right)\omega }$

La energía del sistema Tierra-Luna en dicho instante es

${\displaystyle E=\frac{1}{2}I{\Omega }^2+\frac{1}{2}\left(M_L{r}^2\right){\omega }^2-G\frac{M_T{M}_L}{r}}$

Expresamos el momento angular y la energía en términos de las velocidades angulares Ω y ω

${\displaystyle \begin{array}{l}L=I\Omega +M_L{\left(\frac{G^2{M}_T^2}{\omega }\right)}^{1/3}\\ E=\frac{1}{2}I{\Omega }^2-\frac{1}{2}{M}_L{\left(G{M}_T\omega \right)}^{2/3}\end{array}}$

Despejamos Ω en la primera y sustituimos en la segunda

${\displaystyle E=\frac{1}{2I}{\left(L-M_L{\left(\frac{G^2{M}_T^2}{\omega }\right)}^{1/3}\right)}^2-\frac{1}{2}{M}_L{\left(G{M}_T\omega \right)}^{2/3}}$

Representamos gráficamente la energía E en función de la velocidad angular ω, observando que presenta un mínimo para 1.4·10^-6 rad/s aproximadamente, lo que representa un periodo de rotación de 52 días.

w0=2*pi/(24*3600); %velocidad angular de rotación de la Tierra
r0=384.4e6; %distancia Tierra-Luna
G=6.67e-11; %constante gravitación
MT=5.98e24; %masa de la Tierra
R=6.37e6; %radio de la Tierra
ML=7.34e22; %masa de la Luna

I=2*MT*R^2/5; %momento de inercia de la Tierra
L=I*w0+ML*r0^2*sqrt(G*MT/r0^3); %momento angular
E=@(w) (L-ML*(G^2*MT^2./w).^(1/3)).^2/(2*I)-ML*(G*MT*w).^(2/3)/2;
w2=2*pi/(40*24*60*60); %40 días
w1=2*pi/(60*24*60*60); %60 días
fplot(E,[w1,w2])
grid on
xlabel('\omega')
ylabel('E')
title('Alejamiento de la Luna')

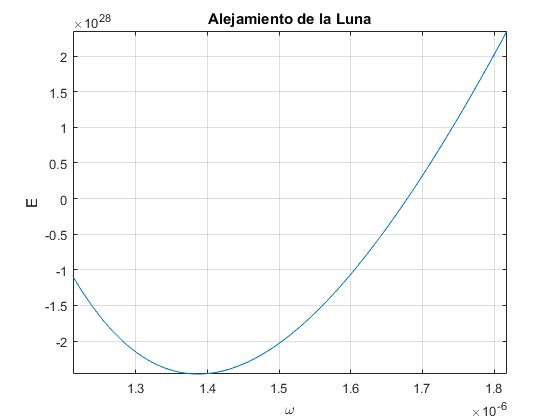
Calculamos la derivada dE/dω y la igualamos a cero

${\displaystyle \frac{dE}{d\omega }=\frac{1}{I}\left(L-M_L{\left(\frac{G^2{M}_T^2}{\omega }\right)}^{1/3}\right)\left(\frac{1}{3}{M}_L{\left(G^2{M}_T^2\right)}^{1/3}{\omega }^{-4/3}\right)-\frac{1}{3}{M}_L{\left(G{M}_T\right)}^{2/3}{\omega }^{-1/3}=0}$

Simplificando nos queda la ecuación

${\displaystyle L-M_L{\left(\frac{G^2{M}_T^2}{\omega }\right)}^{1/3}-I\omega =0}$

Que nos indica que en el mínimo, coinciden las dos velocidades angulares: ω y Ω

Utilizamos la función fzero de MATLAB para calcular la raíz de la ecuación

>> f=@(x) L-ML*(G^2*MT^2/x)^(1/3)-I*x;
>> w_min=fzero(f, 1.4e-6);
w_min =   1.3868e-06
>> (2*pi/w_min)/(24*3600)
ans =   52.4374

El periodo es 52.4374 días, el mismo resultado que hemos obtenido en el apartado anterior

Nos quedaría calcular la derivada segunda de la energía d²E/dt², para verificar que se trata de un mínimo, es decir de una situación de equilibrio estable.

Mecanismo del alejamiento de la Luna

Vamos a analizar las causas por las que disminuye la velocidad angular de rotación Ω de la Tierra y aumenta la distancia r entre el centro de la Tierra y el centro de la Luna, mediante un modelo muy simple

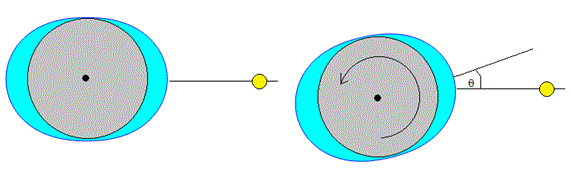
Supondremos que la Tierra está cubierta por una capa esférica homogénea de agua, las fuerzas de marea son máximas y por tanto, la elevación de la capa de agua, en la línea que une la Luna y la Tierra tal como se muestra exageradamente en la figura de la izquierda

Debido a la rotación de la Tierra, las máximas elevaciones del agua de mar no están en la línea que une el centro de la Tierra y el centro de la Luna (figura de la derecha) lo que produce una transferencia de momento angular desde el movimiento de rotación de la Tierra alrededor de su eje hacia el movimiento de traslación de la Luna alrededor de la Tierra como vamos a comprobar seguidamente

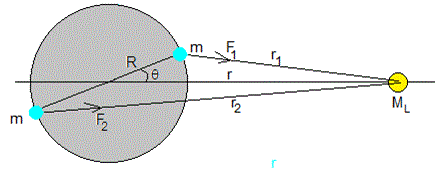
Para que el cálculo sea sencillo, sutituiremos la masas de agua en los extremos del diámetro de la Tierra, por dos masas puntuales m, giradas un pequeño ángulo θ respecto de la línea que une el centro de la Tierra y la Luna

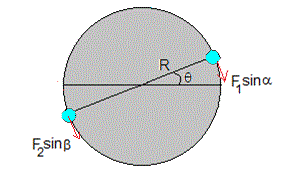
Calculamos el módulos de las fuerzas F₁ y F₂ que ejerce la Luna sobre dichas masas puntuales

${\displaystyle \begin{array}{l}{F}_1=G\frac{M_{L}m}{r_1^2}\\ F_2=G\frac{M_{L}m}{r_2^2}\end{array}}$

Calculamos el momento resultante de ambas fuerzas respecto del centro de la Tierra

${\displaystyle M=-F_{1}R\sin \alpha +F_{2}R\sin \beta }$

Relacionamos los ángulos α y β, y las distancias r₁ y r₂ con r y el ángulo θ en los triángulos OCB y OAB

${\displaystyle \begin{array}{l}{r}_1^2=r^2+R^2-2rR\cos \theta \\ r_2^2=r^2+R^2+2rR\cos \theta \\ \frac{r}{\sin \alpha }=\frac{r_1}{\sin \theta }\\ \frac{r}{\sin \beta }=\frac{r_2}{\sin \left(180-\theta \right)}\end{array}}$

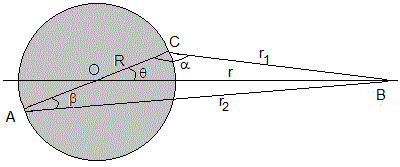
El momento total M es

${\displaystyle M=-G\frac{M_{L}m}{r_1^2}R\frac{r\sin \theta }{r_1}+G\frac{M_{L}m}{r_2^2}R\frac{r\sin \theta }{r_2}=GMm\left(\frac{1}{r_2^3}-\frac{1}{r_1^3}\right)Rr\sin \theta }$

Vamos a obtener una expresión mucho más simple haciendo algunas aproximaciones: (R/r)²≈0, (1+x)ⁿ≈1+nx con x<<1

${\displaystyle M=-3G{M}_{L}m\frac{R^2}{r^3}\sin \left(2\theta \right)}$

Este momento desaparecerá cuando la velocidad angular de rotación Ω de la Tierra se haga igual a la velocidad angular ω de la Luna en su órbita alrededor de la Tierra.

El momento M frena el movimiento de rotación de la Tierra

Aplicamos la ecuación de la dinámica de rotación de un sólido, M=dL/dt, para obtener la variación de la velocidad angular de rotación Ω de la Tierra

${\displaystyle M=\left(\frac{2}{5}{M}_T{R}^2\right)\frac{d\Omega }{dt}}$

En un itervalo de tiempo pequeño, por ejemplo Δt=1 año, el cambio de velocidad angular de rotación ΔΩ es

${\displaystyle \Delta \Omega =-\frac{15}{2}\frac{G{M}_{L}m}{M_T{r}_0^3}\sin \left(2\theta \right)\Delta t}$

Sea m=3.6·10¹⁶ kg, θ=3°, r₀=384.4·10⁶ m. El cambio de velocidad angular de rotación es ΔΩ=-1.2828·10^-14 rad/s

El cambio en la duración del día es

${\displaystyle \begin{array}{l}P=\frac{2\pi }{\Omega }\\ \Delta P=-\frac{2\pi }{{\Omega }_0^2}\Delta \Omega \end{array}}$

El resultado es ΔP=1.52·10^-5 s

El momento M incrementa la distancia r entre el centro de la Tierra y de la Luna

Aplicamos la ecuación de la dinámica de rotación M=dL/dt

${\displaystyle M=-\frac{d}{dt}\left(M_L{r}^2\omega \right)=-\frac{d}{dt}\left(M_L\sqrt{G{M}_T}\sqrt{r}\right)=-\frac{1}{2}\frac{M_L\sqrt{G{M}_T}}{\sqrt{r}}\frac{dr}{dt}}$

En un intervalo de tiempo pequeño, por ejemplo Δt=1 año el cambio de la distancia entre el centro de la Tierra y la Luna, Δr es

${\displaystyle \Delta r=6\sqrt{\frac{G}{M_T}}\frac{R^2}{r_0^2\sqrt{r_0}}\sin \left(2\theta \right)\Delta t}$

Con los mismos datos del apartado anterior: m=3.6·10¹⁶ kg, θ=3°, r₀=384.4·10⁶ m. El cambio de de la distancia es Δr=0.0333 m en un año

Balance energético

La energía del sistema Tierra-Luna, se compone de: la energía cinética de rotación de la Tierra alrededor de su eje fijo con velocidad angular Ω, la energía cinética de la Luna, que describe una órbita circular con velocidad constante ωr y la energía potencial de interacción entre la Tierra y la Luna separadas una distancia r

${\displaystyle E=\frac{1}{2}\left(\frac{2}{5}{M}_T{R}^2\right){\Omega }^2+\frac{1}{2}\left(M_L{r}^2\right){\omega }^2+\left(-G\frac{M_T{M}_L}{r}\right)}$

Teniendo en cuenta que la Luna se mueve en una trayectoria circular de radio r con velocidad angular ω²=GM_T/r³. La expresión de la energía se reduce a

${\displaystyle E=\frac{1}{2}\left(\frac{2}{5}{M}_T{R}^2\right){\Omega }^2-\frac{1}{2}G\frac{M_T{M}_L}{r}}$

La variación de energía ΔE en un intervalo pequeño Δt

${\displaystyle \Delta E=\left(\frac{2}{5}{M}_T{R}^2\right){\Omega }_0\Delta \Omega +\frac{1}{2}G\frac{M_T{M}_L}{r_0^2}\Delta r}$

Con los resultados obtenidos anteriormente, ΔΩ=-1.2828·10^-14 rad/s, Δr=0.0333 m, obtenemos ΔE=-8.72·10¹⁹ J

Referencias

Problema de la XL Olimpiada Internacional de Física. Mérida, México, 2009

Para el apartado, Energía mínima

Lim Yung-kuo. Problems and Solutions on Mechanics. World Scientific (1994). Problem 1176, pp. 286-288