El efecto Oberth

Una pelota de masa m inicialmente en reposo es golpeada por la raqueta de un tenista, que le proporciona un impulso (una fuerza F intensa durante un corto intervalo de tiempo Δt) de módulo I=mu, la pelota modifica su momento lineal en mu, siendo u su velocidad inmediatamente después de ser golpeada

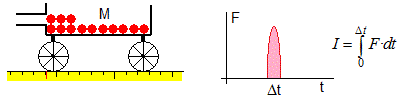
Supongamos un carro inicialmente en reposo, de masa M que contiene n bolas de masa m cada una. El carro tiene un dispositivo que proporciona un impulso I=mu a la bola que dispara y a su vez este impulso modifica la velocidad del carro cuya masa ha disminuido en m.

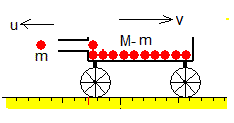
En el instante inicial t=0, el carro dispara la primera bola de masa m con una velocidad u. El carro pierde una masa m y adquiere una velocidad v. Si el carro estaba inicialmente en reposo, su momento lineal es cero. El impulso I=mu modifica su momento lineal.

$\begin{array}{l} (M - m) v = m u \\ v = \frac{m u}{M - m} \end{array}$

La variación de energía antes y despues del disparo de la bola es

$Δ E_{q} = \frac{1}{2} m u^{2} + \frac{1}{2} (M - m) v^{2} = \frac{1}{2} m u^{2} (1 + \frac{m}{M - m})$

Si el carro ya estaba en movimiento con velocidad V

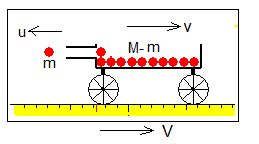
Las velocidades del carro v_n y la bola v_g respecto a Tierra son

$\begin{array}{l} v_{n} = v + V = \frac{m u}{M - m} + V \\ u_{g} = - u + V \end{array}$

La velocidad del carro ha aumentado y la de la bola ha disminuido

La variación de energía antes y después del disparo de la bola es

$\begin{array}{l} Δ E = \frac{1}{2} m u_{g}^{2} + \frac{1}{2} (M - m) v_{n}^{2} - \frac{1}{2} M V^{2} = \frac{1}{2} m {(- u + V)}^{2} + \frac{1}{2} (M - m) {(V + \frac{m u}{M - m})}^{2} - \frac{1}{2} M V^{2} = \\ \frac{1}{2} m u^{2} (1 + \frac{m}{M - m}) \end{array}$

Como cabría esperar la variación de energía no cambia, ΔE=ΔE_q

Impulso en el perigeo

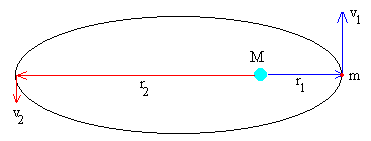
En la figura, se muestra una nave espacial que describe una trayectoria elíptica alrededor de la Tierra cuyo centro está situado en uno de sus focos. La distancia de máximo acercamiento (perigeo) es r₁ y la de máximo alejamiento (apogeo) r₂. Las velocidades que lleva el cuerpo en estas dos posiciones extremas son v₁ y v₂ respectivamente. La constancia del momento angular y de la energía nos permite relacionar estas cuatro magnitudes.

$\begin{array}{l} m r_{1} v_{1} = m r_{2} v_{2} \\ \frac{1}{2} m v_{1}^{2} - \frac{G m M}{r_{1}} = \frac{1}{2} m v_{2}^{2} - \frac{G m M}{r_{2}} \end{array}$

Conocido r₁ y r₂ calculamos v₁ y v₂.

$v_{2} = \sqrt{\frac{2 G M_{T} r_{1}}{r_{2} (r_{1} + r_{2})}} v_{1} = \sqrt{\frac{2 G M_{T} r_{2}}{r_{1} (r_{1} + r_{2})}}$

La energía de la nave espacial de masa M es

$E = \frac{1}{2} M v_{1}^{2} - G \frac{M_{T} M}{r_{1}}$

Siendo R el radio de la Tierra y M_T su masa.

El momento angular, L=M·r₁v₁=M·r₂v₂

Supongamos una nave espacial de masa M, contiene n fracciones de combustible de masa m cada una.

Al pasar por el perigeo, la nave espacial expulsa una fracción m de combustible con velocidad u respecto de la nave. La velocidad de la nave v_n y de la fracción de combustible v_g respecto de Tierra es

$\begin{array}{l} v_{n} = \frac{m u}{M - m} + v_{1} \\ u_{g} = - u + v_{1} \end{array}$

La variación de energía antes y después de la expulsión de la fracción de combustible como hemos mostrado al principio de esta página es ΔE_q

$Δ E = \frac{1}{2} m u_{g}^{2} + \frac{1}{2} (M - m) v_{n}^{2} - \frac{1}{2} M v_{1}^{2} = \frac{1}{2} m u^{2} (1 + \frac{m}{M - m})$

Trayectorias de la nave espacial y de la fracción de combustible

La ecuación de la trayectoria de un cuerpo celeste de masa m dependerá de su energía E y momento angular L

$r = \frac{d}{1 + ε \cos θ} ε = \sqrt{1 + \frac{2 L^{2} E}{m^{3} G^{2} M_{T}^{2}}} d = \frac{L^{2}}{G M_{T} m^{2}}$

Trayectoria de la nave espacial

La energía y el momento angular son

$\begin{array}{l} L_{n} = (M - m) r_{1} v_{n} \\ E_{n} = \frac{1}{2} (M - m) v_{n}^{2} - G \frac{M_{T} (M - m)}{r_{1}} \end{array}$

Trayectoria de la fracción de combustible

La energía y el momento angular son

$\begin{array}{l} L_{g} = m r_{1} v_{g} \\ E_{g} = \frac{1}{2} m v_{g}^{2} - G \frac{M_{T} m}{r_{1}} \end{array}$

Ejemplo

Datos de la trayectoria inicial de la nave espacial de masa M

Perigeo, r₁=1.5R
Apogeo, r₂=13.5R
Masa de una fracción de combustible, m=1
Masa de la nave espacial, M=16·m
Velocidad u de salida de los gases respecto de la nave

$u = 1.5 \cdot v_{\infty} = 1.5 \sqrt{\frac{2 G M_{T}}{R}}$

donde v_∞ es la velocidad de escape desde la superficie de la Tierra y R su radio

Para facilitar los cálculos, establecemos un sistema de unidades tal que GM_T/R=1.

m=1; %fracción de combustible
n=16; %número de fracciones
M=n*m;
v_esc=sqrt(2); %velocidad de escape GMp/Rp=1
u=1.5*v_esc; %velocidad de los gases respecto de la nave
r1=1.5; %perigeo
r2=13.5; %apogeo
v1=sqrt(2*r2/((r2+r1)*r1)); %velocidad perigeo
v2=sqrt(2*r1/((r2+r1)*r2)); %velocidad apogeo
E=v1^2/2-1/r1; %energía por unidad de masa

a=(r1+r2)/2; %semieje mayor
c=a-r1;
ex=c/a; %excentricidad
...

Resultados

Velocidad de expulsión de la fracción de combustible respecto a la nave, u=2.1213
Velocidad en el apogeo, v₂=0.1217
Velocidad en el perigeo, v₁=1.0954
Semieje mayor de la elipse, a=7.5
Excentricidad, ε=0.5786, trayectoria elíptica ε<1
Energía de la nave espacial, E=-0.0667, por unidad de masa

La ecuación de la trayectoria es

$r = \frac{d}{1 + ε \cos θ}$

En el perigeo, r₁=d/(1+ε)
En el apogeo, r₂=d/(1-ε)

El eje mayor es 2a=r₁+r₂, por lo que, d=a(1-ε²)

$r = \frac{a (1 - ε^{2})}{1 + ε \cos θ}$

Impulso en el perigeo

...
v=m*u/(M-m);  %incremento de velocidad
E_q=m*u^2/2+(M-m)*v^2/2; %energía consumida
vn=v+v1; %velocidades repecto a Tierra
ug=-u+v1;

%trayectoria hiperbólica de la nave
Ln=r1*vn;
En=vn^2/2-1/r1; %energía por unidad de masa
d=Ln^2;
ex=sqrt(1+2*Ln^2*En);
fplot(@(th) d*cos(th)./(1+ex*cos(th)), @(th) d*sin(th)./(1+ex*cos(th)),
[0,acos(-1/ex)-pi/9],'color','k')
%trayectoria elíptica de los gases
Lg=r1*ug;
Eg=ug^2/2-1/r1; %energía por unidad de masa
d=Lg^2;
ex=sqrt(1+2*Lg^2*Eg);
...

Velocidad de la nave espacial, respecto Tierra, v_n=1.2369
Velocidad del fragmento de combustible, respecto Tierra, u_g=-1.0259
Variación de energía antes y después de expulsar la fracción de combustible, ΔE_q=2.4000

Trayectorias:

Nave espacial, masa M-m

Energía e_n y momento angular l_n por unidad de masa

$\begin{array}{l} l_{n} = r_{1} v_{n} \\ e_{n} = \frac{1}{2} v_{n}^{2} - \frac{1}{r_{1}} \end{array}$

l_n=1.8553, e_n=0.0983, como la energía es positiva la trayectoria será hiperbólica, los parámetros d y excentricidad ε valen en el sistema de unidades establecido

$ε = \sqrt{1 + 2 l_{n}^{2} e_{n}} d = l_{n}^{2}$

d=3.4421, ε=1.2948

Fragmento de combustible, masa m

Energía e_g y momento angular l_g por unidad de masa

$\begin{array}{l} l_{g} = r_{1} v_{g} \\ e_{g} = \frac{1}{2} v_{g}^{2} - \frac{1}{r_{1}} \end{array}$

l_g= -1.5388, e_g=-0.1405, como la energía es negativa la trayectoria será elíptica, los parámetros d y excentricidad ε valen en el sistema de unidades establecido

$ε = \sqrt{1 + 2 l_{g}^{2} e_{g}} d = l_{g}^{2}$

d=2.3679, ε=0.5786

La diferencia entre la energía inicial y final del conjunto formado por la nave espacial y la fracción de combustible expulsado respecto de Tierra es

>> En*(M-m)+Eg*m-E*M
ans =    2.4000

Las variables En, Eg y E guardan la energía por unidad de masa. El resultado de la suma, coincide con ΔE_q

Comprobamos que el momento lineal del sistema se mantiene constante inmediatamente antes y después del impulso en el perigeo

momento lineal de la nave junto al combustible, M·v₁
momento lineal de la nave, (M-m)v_n
momento lineal del combustible, m·u_g

>> M*v1
ans =   18.6226
>> (M-m)*vn+m*ug
ans =   18.6226

Unimos las dos porciones de código, y añadimos el código para representar la trayectoria inicial de la nave espacial de masa M (azul) y la trayectoria del fragmento de combustible de masa m (roja) y de la nave de masa M-m después de haber expulsado el fragmento de combustible (negra)

m=1; %fracción de combustible
n=16; %número de fracciones
M=n*m; %masa inicial de la nave espacial
v_esc=sqrt(2); %velocidad de escape GM_T/R=1
u=1.5*v_esc; %velocidad de los gases respecto de la nave
r1=1.5; %perigeo
r2=13.5; %apogeo
%semieje mayor a=(r1+r2)/2=7.5
v1=sqrt(2*r2/((r2+r1)*r1)); %velocidad perigeo
v2=sqrt(2*r1/((r2+r1)*r2)); %velocidad apogeo
E=v1^2/2-1/r1; %energía por unidad de masa

a=(r1+r2)/2; %semieje mayor
c=a-r1;
ex=c/a; %excentricidad
hold on
fplot(@(th) a*(1-ex^2)*cos(th)./(1+ex*cos(th)), @(th) a*(1-ex^2)*sin(th)./
(1+ex*cos(th)),[0,pi],'lineStyle','--','color','b')
fplot(@(th) a*(1-ex^2)*cos(th)./(1+ex*cos(th)), @(th) a*(1-ex^2)*sin(th)./
(1+ex*cos(th)),[pi,2*pi],'color','b')
plot(0,0,'bo','markersize',5,'markeredgecolor','b','markerfacecolor','b')

v=m*u/(M-m);  %incremento de velocidad
E_q=m*u^2/2+(M-m)*v^2/2; %energía consumida
vn=v1+v; %velocidades repecto a Tierra en el perigeo
ug=-u+v1;

%trayectoria de la nave
Ln=r1*vn;
En=vn^2/2-1/r1;
d=Ln^2;
ex=sqrt(1+2*Ln^2*En);
fplot(@(th) d*cos(th)./(1+ex*cos(th)), @(th) d*sin(th)./(1+ex*cos(th)),
[0,acos(-1/ex)-pi/9],'color','k')
%trayectoria de la fracción de combustible
Lg=r1*ug;
Eg=ug^2/2-1/r1;
d=Lg^2;
ex=sqrt(1+2*Lg^2*Eg);
fplot(@(th) d*cos(th)./(1+ex*cos(th)), @(th) d*sin(th)./(1+ex*cos(th)),
[0,2*pi],'color','r')

%Energías
% E_q debe ser igual a En*(M-m)+Eg*m-E*M
hold off
axis equal
axis off

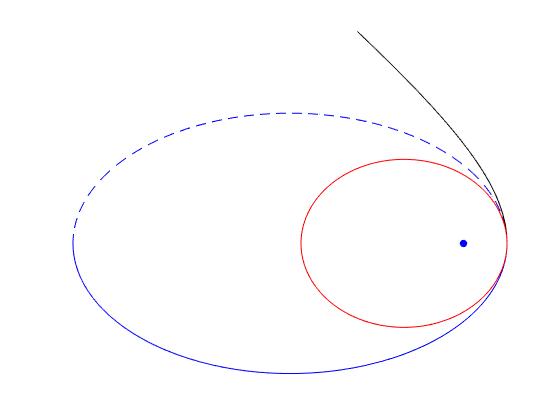
La figura, muestra la trayectoria inicial elíptica (azul) de la nave espacial de masa M, cuando llega al perigeo expulsa una fracción de combustible de masa m. La nave espacial de masa M-m describe una trayectoria hiperbólica (negro), la fracción de combustible una trayectoria elíptica (rojo)

Energías

En el sistema de referencia de la nave, hemos deducido

$\begin{array}{l} v = \frac{m u}{M - m} \\ Δ E_{q} = \frac{1}{2} m u^{2} + \frac{1}{2} (M - m) v^{2} \end{array}$

El primer término es la energía cinética de la fracción de combustible expulsado de masa m y el segundo término, la energía cinética de la nave de masa M-m.

En el sistema de referencia de Tierra, la energía del sistema formado por la nave espacial de masa M-m y la fracción de combustible de masa m es

$\begin{array}{l} v_{n} = \frac{m u}{M - m} + v_{1} \\ u_{g} = - u + v_{1} \\ E = \frac{1}{2} m u_{g}^{2} + \frac{1}{2} (M - m) v_{n}^{2} \end{array}$

v₁ es la velocidad de la nave espacial en el perigeo

En las figura, se muestra en dos digramas de tarta, las proporciones de energía cinética de la fracción de combustible expulsado y de la nave, a la izquierda, en el sistema de referencia de la nave cuando se mueve con velocidad v₁, a la derecha, en el sistema de referencia de Tierra.

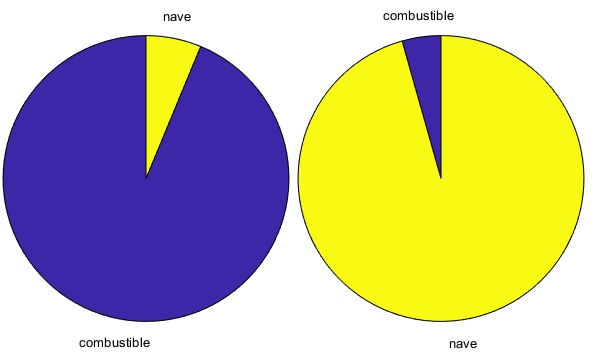
El código para crear estos dos diagramas es

>> E_q=m*u^2/2+(M-m)*v^2/2;
>> Et=m*ug^2/2+(M-m)*vn^2/2;
>> pie([m*u^2/(2*E_q);(M-m)*v^2/(2*E_q)],{'combustible','nave'})
>> pie([m*ug^2/(2*Et);(M-m)*vn^2/(2*Et)],{'combustible','nave'})

Actividades

Creamos una animación, de la figura hecha con MATLAB que muestra la trayectoria

elíptica de la nave espacial desde el apogeo al perigeo (azul)
elíptica de la fracción de combustible expulsado en el perigeo (roja)
hiperbólica de la nave espacial de masa M-m después de haber expulsado la fracción de combustible (negra)

En la parte superior, se muestran las proporciones de energía que lleva cada uno de los dos cuerpos

A la izquierda, en el sistema de referencia de la nave con velocidad v₁ en el perigeo
A la derecha, en el sistema de referencia ligado a Tierra

En esencia el efecto Olberth se puede resumir en que un pequeño cambio v en la velocidad de la nave espacial debido al impulso del comustible expulsado, da lugar a un gran cambio en su energía cinética, si la velocidad de la nave espacial v₁ es grande

Impulso en el apogeo

Al pasar por el apogeo, la nave espacial expulsa una fracción m de combustible con velocidad u respecto de la nave. La velocidad de la nave v_n y de la fracción de combustible v_g respecto de Tierra es

$\begin{array}{l} v_{n} = \frac{m u}{M - m} + v_{2} \\ u_{g} = - u + v_{2} \end{array}$

El script es similar, basta sustituir la distancia r₁ y velocidad v₁ en el perigeo, por la distancia r₂ y velocidad v₂ en el apogeo

m=1; %fracción de combustible
n=16; %número de masas
M=n*m; %masa inicial de la nave espacial
v_esc=sqrt(2); %velocidad de escape GMp/Rp=1
u=1.5*v_esc; %velocidad d elos gases respecto de la nave
r1=1.5; %perigeo
r2=13.5; %apogeo
%semieje mayor a=(r1+r2)/2=7.5
v1=sqrt(2*r2/((r2+r1)*r1)); %velocidad perigeo
v2=sqrt(2*r1/((r2+r1)*r2)); %velocidad apogeo
E=v2^2/2-1/r2; %energía por unidad de masa

a=(r1+r2)/2; %semieje mayor
c=a-r1;
ex=c/a; %excentricidad
hold on
fplot(@(th) a*(1-ex^2)*cos(th)./(1+ex*cos(th)), @(th) a*(1-ex^2)*sin(th).
/(1+ex*cos(th)),[0,pi],'color','b')
fplot(@(th) a*(1-ex^2)*cos(th)./(1+ex*cos(th)), @(th) a*(1-ex^2)*sin(th).
/(1+ex*cos(th)),[pi,2*pi],'lineStyle','--','color','b')
plot(0,0,'bo','markersize',5,'markeredgecolor','b','markerfacecolor','b')

v=m*u/(M-m);  %incremento de velocidad
E_q=m*u^2/2+(M-m)*v^2/2; %energía consumida
vn=v+v2; %velocidades repecto a Tierra en el apogeo
ug=-u+v2;

%trayectoria de la nave
Ln=r2*vn;
En=vn^2/2-1/r2;
d=Ln^2;
ex=sqrt(1+2*Ln^2*En);
fplot(@(th) d*cos(th)./(1+ex*cos(th)), @(th) d*sin(th)./(1+ex*cos(th)),
[0,2*pi],'color','k')
%trayectoria de la fracción de combustible
Lg=r2*ug;
Eg=ug^2/2-1/r2;
d=Lg^2;
ex=sqrt(1+2*Lg^2*Eg);
fplot(@(th) -d*cos(th)./(1+ex*cos(th)), @(th) d*sin(th)./(1+ex*cos(th)),
[0,acos(-1/ex)-pi/4],'color','r')

hold off
axis equal
axis off

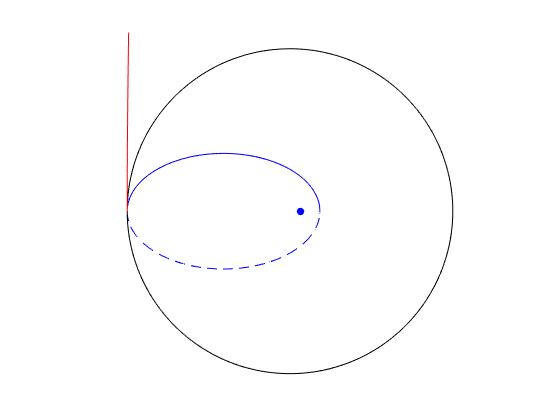
La figura, muestra la trayectoria inicial elíptica (azul) de la nave espacial de masa M, cuando llega al apogeo expulsa una fracción de combustible de masa m. La nave espacial de masa M-m describe una trayectoria casi circular (negro), la fracción de combustible una trayectoria hiperbólica de excentricidad ε=53 (rojo)

Comprobamos que el momento lineal del sistema se mantiene constante inmediatamente antes y después del impulso en el apogeo

momento lineal de la nave junto al combustible, M·v₂
momento lineal de la nave, (M-m)v_n
momento lineal del combustible, m·u_g

>> M*v2
ans =    1.9475
>> (M-m)*vn+m*ug
ans =    1.9475

Actividades

Creamos una animación, de la figura hecha con MATLAB que muestra la trayectoria

elíptica de la nave espacial desde el perigeo al apogeo (azul)
hiperbólica de la fracción de combustible expulsado en el apogeo (roja)
elíptica (casi circular) de la nave espacial de masa M-m después de haber expulsado la fracción de combustible (negra)

En la parte derecha, se muestran las proporciones de energía que lleva cada uno de los dos cuerpos

Arriba, en el sistema de referencia de la nave con velocidad v₂ en el apogeo
Abajo, en el sistema de referencia ligado a Tierra

Comparamos las dos animaciones: impulso en el perigeo e impulso en el apogeo y vemos la ventaja de la primera sobre la segunda

Impulso en cualquier posición comprendida entre el perigeo y el apogeo

En la página titulada Solución numérica de las ecuaciones del movimiento se estudia el movimiento de un cuerpo de masa m atraído por otro cuerpo de masa M_T por ejemplo, la Tierra

$\begin{array}{l} m \frac{d^{2} x}{d t^{2}} = - G \frac{m M_{T}}{r^{2}} \frac{x}{r} \\ m \frac{d^{2} y}{d t^{2}} = - G \frac{m M_{T}}{r^{2}} \frac{y}{r} \end{array}$

Establecemos un sistema de unidades, tomando como unidad de longitud el radio R de la Tierra y GM_T=1. Las ecuaciones del movimiento se escriben

$\begin{array}{l} {\begin{cases} \frac{d^{2} x}{d t^{2}} = - \frac{x}{r^{3}} \\ \frac{d^{2} y}{d t^{2}} = - \frac{y}{r^{3}} \end{cases} \\ r^{2} = x^{2} + y^{2} \end{array}$

Para una trayectoria elíptica de perigeo r₁ y apogeo r₂, el periodo P es

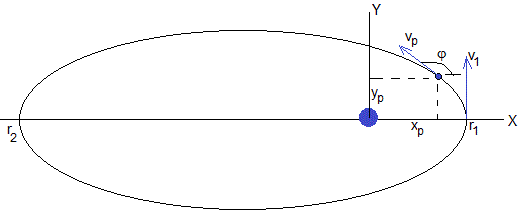
$\begin{array}{l} P^{2} = \frac{4 π^{2} a^{3}}{(G M_{T})} \\ P = 2 π {(\frac{r_{1} + r_{2}}{2})}^{3 / 2} \end{array}$

La nave espacial sale en el instante t=0, del perigeo, en el instante t_I<P/2, enciende durante un tiempo muy corto los motores cuando se encuentra en la posición (x_p, y_p) y lleva una velocidad v_p cuya dirección es tangente a la trayectoria que forma un ángulo φ con el eje X.

Movimiento de la nave espacial

La trayectoria de la nave espacial entre los instantes t=0 y t_I se obtiene resolviendo el sistema de dos ecuaciones diferenciales con las siguientes condiciones iniciales: en el instante t=0

x=r₁, y=0, posición del perigeo
dx/dt=0, dy/dt=v₁, velocidad en el perigeo

Movimiento de la fracción de combustible

La velocidad de la fracción de combustible, en la dirección tangente a la trayectoria en (x_p, y_p), será u_g=-u+v_p

La trayectoria de la fracción de combustible a partir del instante t_I se obtiene resolviendo el sistema de dos ecuaciones diferenciales con las siguientes condiciones iniciales: en el instante t=t_I

x=x_p, y=y_p
dx/dt=u_gcosφ, dy/dt=u_gsinφ

Movimiento de la nave espacial sin la fracción de combustible

La velocidad de la nave espacial después del impulso, en la dirección tangente a la trayectoria en (x_p, y_p), será

$v_{n} = \frac{m u}{M - m} + v_{p}$

La trayectoria de la nave espacial sin la fracción de combustible a partir del instante t_I se obtiene resolviendo el sistema de dos ecuaciones diferenciales con las siguientes condiciones iniciales: en el instante t=t_I

x=x_p, y=y_p
dx/dt=v_ncosφ, dy/dt=v_nsinφ

m=1; %fracción de combustible
n=16; %número de masas
M=n*m; %masa inicial de la nave espacial
v_esc=sqrt(2); %velocidad de escape GMp/Rp=1
u=1.5*v_esc; %velocidad de los gases respecto de la nave
v=m*u/(M-m);  %incremento de velocidad
r1=1.5; %perigeo
r2=13.5; %apogeo
%semieje mayor a=(r1+r2)/2=7.5
v1=sqrt(2*r2/((r2+r1)*r1)); %velocidad perigeo
p_2=pi*sqrt((r1+r2)/2)*(r1+r2)/2; % mitad de periodo

hold on
plot(0,0,'bo','markersize',5,'markeredgecolor','b','markerfacecolor','b')
%nave espacial y combustible
tImpulso=0.1*p_2; %tiempo de impulso
if tImpulso>0
    fg=@(t,x)[x(2);-x(1)/(sqrt(x(1)*x(1)+x(3)*x(3)))^3; x(4); 
-x(3)/(sqrt(x(1)*x(1)+x(3)*x(3)))^3];
    [~,x]=ode45(fg,[0,tImpulso],[r1,0,0,v1]);
    plot(x(:,1),x(:,3),'b')
    vp=sqrt(x(end,2)^2+x(end,4)^2);
    ang=atan2(x(end,4),x(end,2));
    xp=x(end,1); %posición en el instante de impulso
    yp=x(end,3);
else %perigeo
    vp=v1;
    ang=pi/2;
    xp=r1;
    yp=0;
end
vn=vp+v; %velocidades repecto a Tierra
ug=-u+vp;
plot(xp,yp,'ko','markersize',3,'markeredgecolor','k','markerfacecolor','k')
%trayectoria nave
[~,x]=ode45(fg,[0,10],[xp,vn*cos(ang),yp,vn*sin(ang)]);
plot(x(:,1),x(:,3),'k')
%trayectoria combustible
[t,x]=ode45(fg,[0,4],[xp,ug*cos(ang),yp,ug*sin(ang)]);
plot(x(:,1),x(:,3),'r')

hold off
axis equal
grid on
xlabel('x')
ylabel('y');
title('Trayectorias')

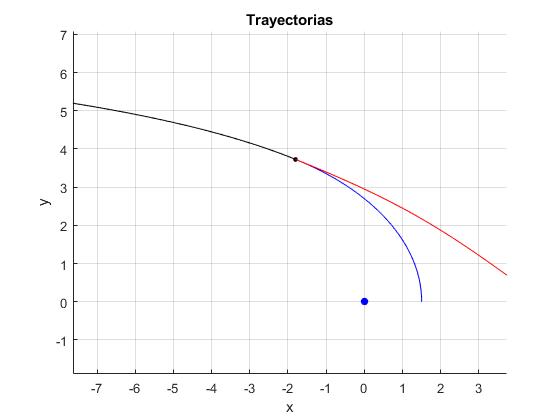
Actividades

Se introduce

El instante, t_I en el control titulado Tiempo impulso, en la que la nave espacial enciende durante un tiempo muy corto, los motores para expulsar una fracción de combustible. 0 significa t_I=0, en la posición del perigeo y 1 el instante t_I=P/2, en la posición del apogeo

Tiempo impulso:

Aplicación del efecto Oberth

Una nave espacial de masa inicial m₀, enciende sus motores durante un breve tiempo, la nave espacial de masa final m, incrementa su velocidad o la disminuye, dependiendo si se proporciona el impulso en sentido de la velocidad inicial o en el contrario

$Δ v = v - v_{0} = u \ln (\frac{m_{0}}{m})$

Siendo u la velocidad de escape de los gases respecto de la nave espacial. El combustible gastado es la diferencia de masas m₀-m. Midiendo los cambios de velocidad Δv determinamos la cantidad de combustible quemado

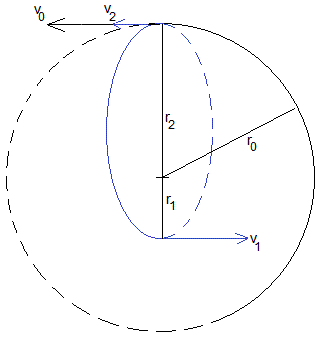
Supongamos que la nave espacial describe una órbita circular de radio r₀ con velocidad v₀. Por la dinámica del movimiento circular uniforme

$m_{0} \frac{v_{0}^{2}}{r_{0}} = \frac{G M_{T} m_{0}}{r_{0}^{2}}, v_{0} = \sqrt{\frac{G M_{T}}{r_{0}}}$

Siendo M_T la masa de la Tierra

La nave espacial enciende sus motores con el fin de disminuir su velocidad de v₀ a v₂. Siendo ésta, la velocidad de la nave espacial en el apogeo r₂=r₀ de una trayectoria elíptica, cuyo perigeo es r₁. La variación de velocidad en el apogeo es

$\begin{array}{l} Δ v_{a} = v_{2} - v_{0} = \sqrt{\frac{2 G M_{T} r_{1}}{r_{2} (r_{1} + r_{2})}} - \sqrt{\frac{G M_{T}}{r_{0}}} = - \sqrt{\frac{G M_{T}}{r_{0}}} (1 - \sqrt{\frac{2 r_{1}}{r_{1} + r_{0}}}) \\ Δ v_{a} = - v_{0} (1 - \sqrt{\frac{2 r_{1}}{r_{1} + r_{0}}}) \end{array}$

Cuando llega al perigeo con velocidad v₁, enciende los motores (durante un tiempo muy corto) para incrementar su velocidad con el fin de describir una trayectoria hiperbólica que la lleve al infinito (muy lejos) con velocidad v_∞

La velocidad v_p que hay que proporcionar a la nave espacial en el perigeo para que alcance el infinito con velocidad v_∞ es

$\frac{1}{2} m v_{\infty}^{2} = \frac{1}{2} m v_{p}^{2} - \frac{G M_{T} m}{r_{1}}$

La nave espacial ha de incrementar su velocidad de v₁ a v_p

$\begin{array}{l} Δ v_{p} = v_{p} - v_{1} = \sqrt{v_{\infty}^{2} + \frac{2 G M_{T}}{r_{1}}} - \sqrt{\frac{2 G M_{T} r_{0}}{r_{1} (r_{1} + r_{0})}} = \sqrt{\frac{G M_{T}}{r_{1}}} (\sqrt{2 + \frac{v_{\infty}^{2} r_{1}}{G M_{T}}} - \sqrt{\frac{2 r_{0}}{r_{1} + r_{0}}}) \\ Δ v_{p} = v_{0} (\sqrt{2 \frac{r_{0}}{r_{1}} + \frac{v_{\infty}^{2}}{v_{0}^{2}}} - \sqrt{\frac{2 r_{0}^{2}}{r_{1} (r_{1} + r_{0})}}) \end{array}$

Cuando la nave espacial disminuye su velocidad y cuando la incrementa, consume combustible, el total es

$Δ v = | Δ v_{a} | + Δ v_{p} = v_{0} (1 + \sqrt{2 \frac{r_{0}}{r_{1}} + \frac{v_{\infty}^{2}}{v_{0}^{2}}} - \sqrt{2 + 2 \frac{r_{0}}{r_{1}}})$

Ejempo

La nave espacial describe una órbita circular geoestacionaria de radio r₀=6.6327·R. Siendo R el radio de la Tierra. A continuación, descibirá una trayectoria semielíptica de perigeo r₁=2R y finalmente, una trayectoria parabólica que le lleve al infinito con velocidad, v_∞=1.5·v₀

Para facilitar los cálculos establecemos un sistema de unidades tal que GM_T/R=1

Orbita circular de radio r₀=6.6327·R

$v_{0} = \sqrt{\frac{1}{r_{0}}} = 0.3883$

Velocidad en el apogeo, r₂=r₀ y variación de velocidad en el apogeo

$v_{2} = \sqrt{\frac{2 r_{1}}{r_{2} (r_{1} + r_{2})}} = 0.2643$

La variación de velocidad en el apogeo es Δv_a=0.2643-0.3883=-0.1240

Velocidad en el perigeo, r₁=2R y variación de velocidad en el perigeo

$v_{1} = \sqrt{\frac{2 r_{0}}{r_{1} (r_{1} + r_{0})}} = 0.8765$

Para que la nave espacial llegue al infinito con velocidad nula, v_∞=1.5·v₀. La velocidad v_p debería ser

$\begin{array}{l} \frac{1}{2} v_{\infty}^{2} = \frac{1}{2} v_{p}^{2} - \frac{1}{r_{1}} \\ v_{p} = \sqrt{v_{\infty}^{2} + \frac{2}{r_{1}}} = 1.1573 \end{array}$

La variación de velocidad en el perigeo es Δv_p=v_p-v₁=0.2807

La variación total (relacionada con el combustible gastado) es la suma de los valores absolutos de la variación de velocidad en el apogeo y en el perigeo,
Δv=|Δv_a|+Δv_p=0.1240+0.2807=0.4047.

r0=6.6327; %órbita geoestacionaria
r2=r0; %apogeo
r1=2; %perigeo
v0=sqrt(1/r0);
vi=1.5*v0; %velocidad en el infinito
v1=sqrt(2*r2/((r2+r1)*r1)); %velocidad perigeo
v2=sqrt(2*r1/((r2+r1)*r2)); %velocidad apogeo
vp=sqrt(vi^2+2/r1); %trayectoria hiperbólica
DVa=v2-v0; %incrementos de velocidad en el apogeo
DVp=vp-v1; %incrementos de velocidad en el perigeo
DV=v0*(1+sqrt(2*r0/r1+(vi/v0)^2)-sqrt(2+2*r0/r1));

>> DV
DV =  0.4047
>> abs(DVa)+DVp
ans =     0.4047

Comparación

Directamente, desde la órbita circular al infinito

La velocidad con la que se debe lanzar la nave espacial desde la órbita circular de radio r₀ para que alcance el infinito con velocidad v_∞ es

$\frac{1}{2} m v_{\infty}^{2} = \frac{1}{2} m v_{c}^{2} - \frac{G M_{T} m}{r_{0}}$

La variación de velocidad es

$Δ v_{c} = v_{c} - v_{0} = \sqrt{v_{\infty}^{2} + \frac{2 G M_{T}}{r_{0}}} - v_{0} = v_{0} (\sqrt{2 + \frac{v_{\infty}^{2}}{v_{0}^{2}}} - 1)$

La velocidad local de escape v_∞=0 es

$v_{c} = \sqrt{2} v_{0}$

Indirectamente, pasando por una órbita semielíptica, con un perigeo cercano a la superficie de la Tierra

$Δ v = v_{0} (1 + \sqrt{2 \frac{r_{0}}{r_{1}} + \frac{v_{\infty}^{2}}{v_{0}^{2}}} - \sqrt{2 + 2 \frac{r_{0}}{r_{1}}})$

Representamos Δv_c/v₀ (negro) y Δv/v₀ (color) en función de v_∞/v₀, la segunda para dos valores de r₁

r0=6.6327; %órbita geoestacionaria
hold on
for r1=[2,5]
    f=@(x) 1+sqrt(2*r0./r1+x.^2)-sqrt(2+2*r0./r1); %efecto Olberth
    fplot(f,[0,3])
end
g=@(x) sqrt(2+x.^2)-1;      %circular
fplot(g,[0,3],'color','k')
hold off
xlabel('v_\infty/v_0')
ylabel('\Deltav/v_0')
grid on
legend('r_1=2','r_1=5','circular','location','best')
title('Efecto Oberth')

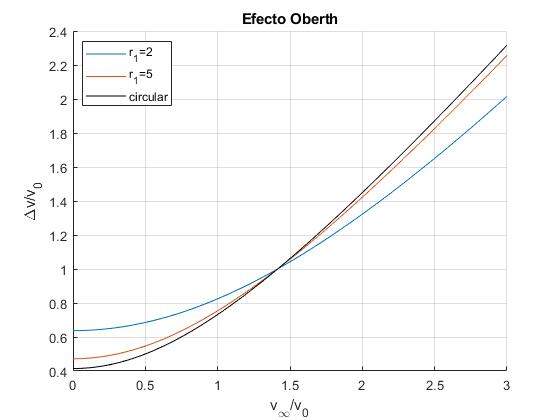
A partir de $\frac{v_{\infty}}{v_{0}} = \sqrt{2}$ , (la intersección de las tres curvas) el efecto Orberth tiene ventaja ya que da lugar a un menor consumo de combustibe, es decir, un menor valor de Δv, esta ventaja es aún mayor cuanto menor sea el radio r₁ del perigeo (curva de color azul)

Actividades

Se introduce

La distancia r₁ al perigeo, en el control titulado Perigeo
La velocidad en el infinito, el cociente v_∞/v₀, en el control titulado Velocidad en el infinito
El radio de la órbita circular se ha fijado en r₀=6.6327·R, siendo R el radio de la Tierra

Observamos el movimiento de la nave espacial en la órbita circular de radio r₀ con velocidad v₀, cuando llega a la parte superior (medio periodo) pone en marcha los motores durante un corto intervalo de tiempo, para disminuir la velocidad de la nave a v₂, siendo ésta la velocidad en el apogeo de la trayectoria semielíptica de perigeo r₁. Cuando llega al perigeo, pone en marcha los motores para incrementar la velocidad de v₁ a v_p para alcanzar el infinito con velocidad v_∞ siguiendo una trayectoria hiperbólica

En la parte izquierda, se muestra los cambios de velocidad

En el apogeo: (v₂-v₀)/v₀ (cantidad negativa, en color amarillo)
En el perigeo: (v_p-v₁)/v₀ (cantidad positiva, en color rosa). La cifra debajo es la altura de la barra, que está relacionada con el combustible gastado, de acuerdo a la fórmula dada al principio de esta sección
La barra derecha (color gris claro), es el cambio de velocidad (v_c-v₀)/v₀ para un impulso directo que lleve a la nave desde la órbita circular de radio r₀ hasta el infinito

Perigeo, r₁:
Velocidad en el infinito, v_∞/v₀:

Referencias

Philip Rodriguez Blanco, Carl E. Mungan. Rocket Propulsion, Classical Relativity, and the Oberth Effect. The Physics Teacher. Vol. 57, October 2019, pp. 439-441

Disponible en la dirección https://aapt.scitation.org/doi/10.1119/1.5126818

Animación: impulso en el perigeo y en el apogeo

https://aapt.scitation.org/doi/suppl/10.1119/1.5126818/suppl_file/439_1-supp.mp4

Philip R. Blanco, Carl E. Mungan. High-speed escape from a circular orbit. Am. J. Phys. 89 (1), January 2021. pp. 72-79

Vídeo resumen del artículo en https://aapt.scitation.org/doi/abs/10.1119/10.0001956

Artículos disponibles en la dirección: https://www.usna.edu/Users/physics/mungan/Publications/Publications.php#fndtn-panel120162017