Un meteorito se dirige radialmente hacia la Tierra

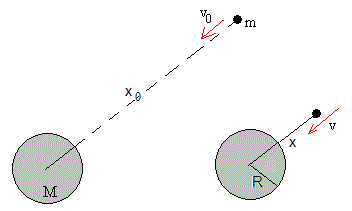
Un meteorito de masa m se mueve hacia la Tierra en dirección radial (eje X). A la distancia x₀ del centro de la Tierra su velocidad es v₀. Calcular la velocidad y el tiempo que tarda en chocar con la superficie de la Tierra.

Supondremos que la Tierra está inmóvil. Aplicamos el principio de conservación de la energía para calcular la velocidad v de impacto con la superficie de la Tierra.

${\displaystyle \begin{array}{l}\frac{1}{2}m{v}_0^2-G\frac{Mm}{x_0}=\frac{1}{2}m{v}^2-G\frac{Mm}{R}\\ v=\sqrt{v_0^2+2GM\left(\frac{1}{R}-\frac{1}{x_0}\right)}\end{array}}$

Es más complicado calcular el tiempo de impacto. La velocidad del meteorito cuando se encuentra a una distancia x del centro de la Tierra es

${\displaystyle \frac{dx}{dt}=-\sqrt{v_0^2+2GM\left(\frac{1}{x}-\frac{1}{x_0}\right)}}$

Integramos para obtener el tiempo t

${\displaystyle \begin{array}{l}t=-{\displaystyle \underset{r_0}{\overset{R}{\int }}\frac{dx}{\sqrt{v_0^2+2GM\left(\frac{1}{x}-\frac{1}{x_0}\right)}}}\\ t=-{\displaystyle \underset{x_0}{\overset{R}{\int }}\sqrt{\frac{x_{0}x}{2GM{x}_0-\left(2GM-x_0{v}_0^2\right)x}}dx}=-{\displaystyle \underset{x_0}{\overset{R}{\int }}\sqrt{\frac{x_{0}x}{a-bx}}dx}\end{array}}$

Hacemos el cambio de variable

${\displaystyle \begin{array}{l}x=\frac{a}{b}{\sin }^2\theta \{\begin{array}{l}a=2GM{x}_0\\ b=2GM-x_0{v}_0^2\end{array}\\ t=-\frac{2a}{b}\sqrt{\frac{x_0}{b}}\underset{{\theta }_0}{\overset{\theta }{{\displaystyle \int }}}{\sin }^{2}d\theta =\frac{a}{b}\sqrt{\frac{x_0}{b}}\left\{\left({\theta }_0-\frac{1}{2}\sin (2{\theta }_0)\right)-\left(\theta -\frac{1}{2}\sin (2\theta )\right)\right\}\end{array}}$

Ejemplo 1

Un meteorito de de masa m se dirige desde el espacio exterior hacia la Tierra. Su velocidad a una distancia de x₀=3.8·10⁷ m del centro de la Tierra es de v₀=30 km/s.
Calcular la velocidad y el tiempo en minutos de su impacto en la superficie de la Tierra

G=6.67e-11;
M=5.98e24; %masa de la Tierra
R=6.37e6; %radio de la Tierra
r0=3.8e7; %distancia inicial
rf=R; %distancia final
v0=30000; %velocidad inicial 
%velocidad final del metoerito en la superficie de la Tierra
v=sqrt(v0^2+2*G*M*(1/rf-1/r0))  

a=2*G*M*r0;
b=2*G*M-r0*v0^2;
fi_0=asin(sqrt(b*r0/a));
fi=asin(sqrt(b*rf/a));
%tiempo en minutos
t=sqrt(a^2*r0/b^3)*((fi_0-sin(2*fi_0)/2)-(fi-sin(2*fi)/2))/60 

v = 3.1690e+04
t =  17.3465

Cuando la partícula parte de x₀ en reposo v₀=0, la expresión del tiempo t que tarda en llegar a la superficie de la Tierra x=R, se simplifica notablemente.

${\displaystyle \begin{array}{l}{\theta }_0=\frac{\pi }{2}\\ \sin \theta =\sqrt{\frac{R}{x_0}}\\ t=r_0\sqrt{\frac{r_0}{2GM}}\left\{\arccos \left(\sqrt{\frac{R}{x_0}}\right)+\sqrt{\frac{R}{x_0}}\sqrt{1-\frac{R}{x_0}}\right\}\end{array}}$

Supongamos que se deja caer una partícula desde una altura de h=10 000 m sobre la superficie de la Tierra, r₀=R+h, calculamos el tiempo que tarda en llegar a la superficie de la Tierra x=R y lo comparamos con el tiempo que se obtendría suponiendo que la aceleración de la gravedad g=GM/R² es constante

${\displaystyle h=\frac{1}{2}g{t}^{2}t=\sqrt{\frac{2h}{g}}}$

G=6.67e-11;
M=5.98e24; %masa de la Tierra
R=6.37e6; %radio de la Tierra
h=10000; %altura
r0=R+h; %distancia inicial al centro de la Tierra
t=r0*sqrt(r0/(2*G*M))*(acos((sqrt(R/r0)))+sqrt(R/r0)*sqrt(1-R/r0));

%aceleración de la gravedad constante
g=G*M/R^2;
t1=sqrt(2*h/g);
disp([t;t1])

   45.1657
   45.1067

Un asteroide se dirige hacia el Sol, su velocidad es de 12 100 m/s a una distancia de r₀=4.5·10¹¹ m. Calcular el tiempo en días que tardará en cruzar la órbita de la Tierra, a una distancia r_f=1.5·10¹¹ m

G=6.67e-11;
M=1.98e30; %masa del Sol
r0=4.5e11; %distancia inicial
v0=12100; %velocidad inicial 
rf=1.5e11;%distancia final

a=2*G*M*r0;
b=2*G*M-r0*v0^2;
fi_0=asin(sqrt(b*r0/a));
fi=asin(sqrt(b*rf/a));
%tiempo en días
t=sqrt(a^2*r0/b^3)*((fi_0-sin(2*fi_0)/2)-(fi-sin(2*fi)/2))/(24*3600)

t =  173.3928

Un proyectil se dispara desde la superficie de la Tierra

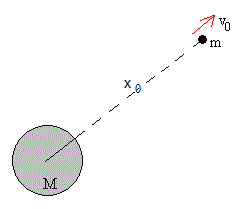
Consideremos un proyectil de masa m que es disparado en dirección radial (eje X) desde una distancia x₀ del centro de la Tierra con velocidad v₀.

Aplicamos el principio de conservación de la energía para calcular la velocidad v=dx/dt cuando el proyectil se encuentra a una distancia x del centro de la Tierra

${\displaystyle \begin{array}{l}\frac{1}{2}m{v}_0^2-G\frac{Mm}{x_0}=\frac{1}{2}m{v}^2-G\frac{Mm}{x}\\ v^2=v_0^2-GM\left(\frac{1}{x_0}-\frac{1}{x}\right)\end{array}}$

Cuando x tiende a infinito, v tiende a

${\displaystyle v_{\infty }^2=v_0^2-\frac{GM}{x_0}}$

La raíz real de v_∞ existe, siempre que la velocidad inicial v₀ sea mayor o igual que v_e, denominada velocidad de escape (mínima necesaria para llevar un cuerpo al infinito con velocidad nula)

${\displaystyle v_0\ge v_e{v}_e=\sqrt{\frac{GM}{x_0}}}$

Cuando se dispara un proyectil desde la posición x₀ con velocidad v₀, existen tres posibilidades

• Que la velocidad inicial del proyectil sea igual a la de escape, v₀=v_e
• Que la velocidad inicial del proyectil sea mayor que la de escape, v₀>v_e
• Que la velocidad inicial del proyectil sea menor que la de escape, v₀<v_e

La velocidad inicial del proyectil es igual a la de escape

Es el caso más sencillo

${\displaystyle \frac{dx}{dt}=\sqrt{\frac{GM}{x}}=v_0\sqrt{\frac{x_0}{x}}}$

Integramos esta ecuación diferencial con las condiciones iniciales: t=0, x=x₀

${\displaystyle \begin{array}{l}\frac{1}{\sqrt{x_0}}{\displaystyle \underset{r_0}{\overset{r}{\int }}\sqrt{x}dx}=v_0{\displaystyle \underset{0}{\overset{t}{\int }}dt}\\ x=x_0{\left(1+\frac{3}{2}\frac{v_{0}t}{x_0}\right)}^{2/3}\end{array}}$

x0=1;
x=@(t) (1+3*t/2).^(2/3);
fplot(x,[0,10])
grid on
ylim([0,7])
xlabel('t')
ylabel('x')
title('v_0=v_e')

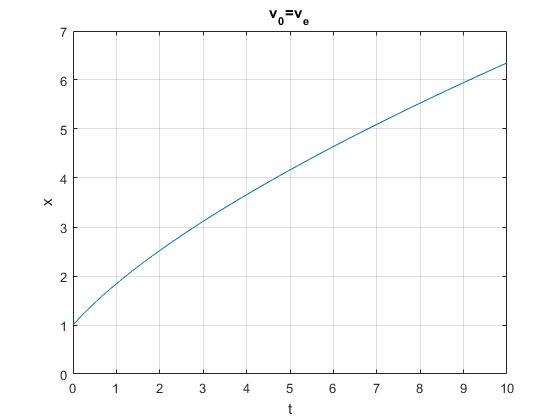
La velocidad inicial del proyectil es mayor a la de escape

Escribimos el principio de conservación de la energía de la forma

${\displaystyle \begin{array}{l}{v}^2=\frac{(v_0^2-v_e^2)x+x_0{v}_e^2}{x}=v_0^2\frac{bx+a}{x}\\ \gamma =\frac{v_0}{v_e}b=1-\frac{1}{{\gamma }^2}a=\frac{x_0}{{\gamma }^2}\\ \frac{dx}{dt}=v_0\sqrt{\frac{bx+a}{x}}\end{array}}$

Si v₀>v_e, entonces γ>1 y b>0, como vemos a>0

Integramos esta ecuación diferencial con las condiciones iniciales: t=0, x=x₀

${\displaystyle \frac{1}{v_0}{\displaystyle \underset{x_0}{\overset{x}{\int }}\sqrt{\frac{x}{bx+a}}dx={\displaystyle \underset{0}{\overset{t}{\int }}dt}}}$

Para resolver la integral de la izquierda, como b>0, hacemos el cambio de variable

${\displaystyle x=\frac{a}{b}{\sinh }^2\theta dx=2\frac{a}{b}\sinh \theta \cosh \theta ·d\theta }$

El integrando es

${\displaystyle {\displaystyle \int \sqrt{\frac{x}{a+bx}}}dx=\frac{2a}{b^{3/2}}{\displaystyle \int {\sinh }^2\theta ·d\theta =}\frac{a}{2b^{3/2}}\left(\sinh (2\theta )-2\theta \right)=\frac{a}{b^{3/2}}\left(\sinh \theta ·\cosh \theta -\theta \right)}$

Deshaciendo el cambio, el integrando es

${\displaystyle {\displaystyle \int \sqrt{\frac{x}{a+bx}}}dx=\frac{a}{b^{3/2}}\left\{\sqrt{1+\frac{bx}{a}}\sqrt{\frac{bx}{a}}-{\sinh }^{-1}\sqrt{\frac{bx}{a}}\right\}}$

>> syms a b positive;
>> syms x;
>> z=int(sqrt(x/(a+b*x)),x)
>> simplify(z)
ans =((x/(a + b*x))^(1/2)*(a + b*x))/b - 
(a*atanh(b^(1/2)*(x/(a + b*x))^(1/2)))/b^(3/2)

En el código, el integrando aparece expresado en términos de tanh^-1θ, comprobamos que es equivalente a expresarlo en términos de sinh^-1θ sabiendo que

${\displaystyle {\tanh }^2\theta =\frac{{\sinh }^2\theta }{1+{\sinh }^2\theta }}$

Expresamos el integrando en términos del parámetro γ=v₀/v_e

${\displaystyle \frac{\gamma }{{\left({\gamma }^2-1\right)}^{3/2}}{x}_0\left\{\sqrt{({\gamma }^2-1)}\sqrt{\frac{x}{x_0}+({\gamma }^2-1)\frac{x^2}{x_0^2}}-{\sinh }^{-1}\sqrt{({\gamma }^2-1)\frac{x}{x_0}}\right\}}$

El tiempo t vale

${\displaystyle t=\frac{\gamma }{{\left({\gamma }^2-1\right)}^{3/2}}\frac{x_0}{v_0}\left\{\begin{array}{l}\sqrt{{\gamma }^2-1}\sqrt{\frac{x}{x_0}+({\gamma }^2-1){\left(\frac{x}{r_0}\right)}^2}-{\sinh }^{-1}\sqrt{({\gamma }^2-1)\frac{x}{x_0}}\\ -\gamma \sqrt{{\gamma }^2-1}+{\sinh }^{-1}\sqrt{{\gamma }^2-1}\end{array}\right\}}$

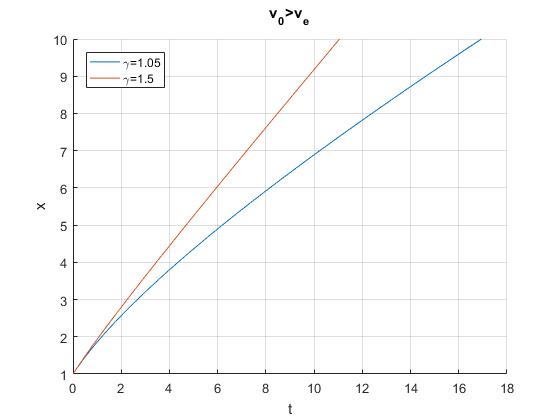
Representamos la función implícita x(t), para dos valores de γ, 1.05 y 1.5

x0=1;
hold on
gamma=1.05;
t=@(x) gamma*(sqrt(gamma^2-1)*sqrt(x+(gamma^2-1)*x.^2)-asinh(sqrt((gamma^2-1)*x))
-gamma*sqrt(gamma^2-1)+asinh(sqrt(gamma^2-1)))/(gamma^2-1)^(3/2);
fplot(t,[x0,10])
gamma=1.5;
t=@(x) gamma*(sqrt(gamma^2-1)*sqrt(x+(gamma^2-1)*x.^2)-asinh(sqrt((gamma^2-1)*x))-
gamma*sqrt(gamma^2-1)+asinh(sqrt(gamma^2-1)))/(gamma^2-1)^(3/2);
fplot(t,[x0,10])
grid on
legend('\gamma=1.05','\gamma=1.5', 'location','northwest')
xlabel('x')
ylabel('t')
view(90,-90)
title('v_0>v_e')

La velocidad inicial del proyectil es menor a la de escape

Escribimos el principio de conservación de la energía de la misma forma que en el apartado anterior

${\displaystyle \begin{array}{l}{v}^2=\frac{(v_0^2-v_e^2)x+x_0{v}_e^2}{x}=v_0^2\frac{bx+a}{x}\\ \gamma =\frac{v_0}{v_e}b=1-\frac{1}{{\gamma }^2}a=\frac{x_0}{{\gamma }^2}\\ \frac{dx}{dt}=v_0\sqrt{\frac{bx+a}{x}}\end{array}}$

Si v₀<v_e, entonces γ<1 y b<0

Integramos esta ecuación diferencial con las condiciones iniciales: t=0, x=x₀

${\displaystyle \frac{1}{v_0}{\displaystyle \underset{x_0}{\overset{x}{\int }}\sqrt{\frac{x}{a-\left|b\right|x}}dx={\displaystyle \underset{0}{\overset{t}{\int }}dt}}}$

Para resolver la integral de la izquierda, hacemos el cambio de variable

${\displaystyle x=\frac{a}{\left|b\right|}{\sin }^2\theta dx=2\frac{a}{\left|b\right|}\sin \theta \cos \theta ·d\theta }$

El integrando es

${\displaystyle \begin{array}{l}{\displaystyle \int \sqrt{\frac{x}{a-\left|b\right|x}}}dx=\frac{2a}{{\left|b\right|}^{3/2}}{\displaystyle \int {\sin }^2\theta ·d\theta =}\frac{a}{{\left|b\right|}^{3/2}}{\displaystyle \int (1-\cos 2\theta )·d\theta =}\\ \frac{a}{{\left|b\right|}^{3/2}}\left(\theta -\frac{1}{2}\sin (2\theta )\right)=\frac{a}{{\left|b\right|}^{3/2}}\left(\theta -\sin \theta \cos \theta \right)\end{array}}$

Deshaciendo el cambio, el integrando es

${\displaystyle {\displaystyle \int \sqrt{\frac{x}{a-\left|b\right|x}}}dx=\frac{a}{{\left|b\right|}^{3/2}}\left\{\arcsin \sqrt{\frac{\left|b\right|x}{a}}-\sqrt{\frac{\left|b\right|x}{a}}\sqrt{1-\frac{\left|b\right|x}{a}}\right\}=}$

>> syms a b positive;
>> syms x;
>> z=int(sqrt(x/(a-b*x)),x) 
>> simplify(z)
ans =(a*atan(b^(1/2)*(x/(a - b*x))^(1/2)))/b^(3/2) - 
((x/(a - b*x))^(1/2)*(a - b*x))/b

En el código, el integrando aparece expresado en términos de tan^-1θ, comprobamos que es equivalente a expresarlo en términos de sin^-1θ sabiendo que

${\displaystyle {\tan }^2\theta =\frac{{\sin }^2\theta }{1-{\sin }^2\theta }}$

Expresamos el integrando en términos del parámetro γ=v₀/v_e

${\displaystyle \frac{\gamma x_0}{{\left(1-{\gamma }^2\right)}^{3/2}}\left\{\arcsin \sqrt{(1-{\gamma }^2)\frac{x}{x_0}}-\sqrt{(1-{\gamma }^2)}\sqrt{\frac{x}{x_0}-(1-{\gamma }^2)\frac{x^2}{x_0^2}}\right\}}$

El tiempo t vale

${\displaystyle t=\frac{\gamma }{{\left(1-{\gamma }^2\right)}^{3/2}}\frac{x_0}{v_0}\left\{\begin{array}{l}\arcsin \sqrt{(1-{\gamma }^2)\frac{x}{x_0}}-\sqrt{1-{\gamma }^2}\sqrt{\frac{x}{x_0}-(1-{\gamma }^2){\left(\frac{x}{x_0}\right)}^2}\\ -\arcsin \sqrt{1-{\gamma }^2}+\gamma \sqrt{1-{\gamma }^2}\end{array}\right\}}$

La velocidad se hace cero cuando a+bx=0, que es la máxima distancia de alejamiento del centro de fuerzas (recuérdese que en este caso b<0). La distancia de máximo alejamiento x_m es

${\displaystyle x_m=\frac{x_0}{1-{\gamma }^2}}$

El tiempo t_m que emplea en alcanza esta posición es

${\displaystyle t_m=\frac{\gamma }{{\left(1-{\gamma }^2\right)}^{3/2}}\frac{x_0}{v_0}\left\{\frac{\pi }{2}-\arcsin \sqrt{1-{\gamma }^2}+\gamma \sqrt{1-{\gamma }^2}\right\}}$

2t_m es el tiempo que tarda en regresar al punto de partida x₀, con velocidad v₀ en sentido contrario

Representamos la función implícita x(t), para γ=0.8

x0=1;
gamma=0.8;
xm=1/(1-gamma^2);
tm=gamma*(pi/2-asin(sqrt(1-gamma^2))+gamma*sqrt(1-gamma^2))/(1-gamma^2)^(3/2);
t=@(x) gamma*(-sqrt(1-gamma^2)*sqrt(x-(1-gamma^2)*x.^2)+asin(sqrt((1-gamma^2)*x))
+gamma*sqrt(1-gamma^2)-asin(sqrt(1-gamma^2)))/(1-gamma^2)^(3/2);
fplot(t,[x0,xm])
grid on
xlabel('x')
ylabel('t')
view(90,-90)
title('v_0<v_e')

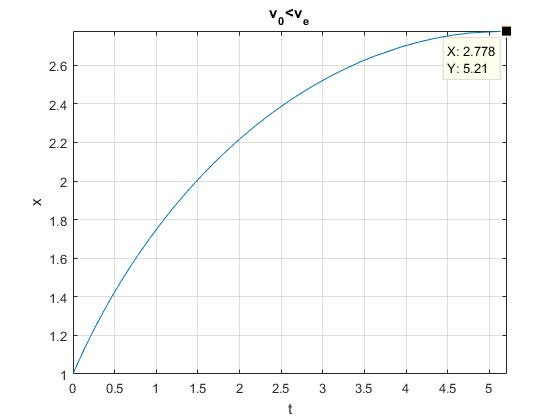
La distancia de máximo alejamiento x_m y el tiempo que emplea en recorrerla t_m son

>> xm
xm =    2.7778
>> tm
tm =    5.2122

Problema de dos cuerpos

Supongamos que inicialmente los dos cuerpos están en reposo, separados una distancia r entre ambos. El centro de masa estará en reposo a una distancia r₁ del cuerpo de masa m₁ y a una distancia r₂ del cuerpo de masa m₂, como vemos en la figura.

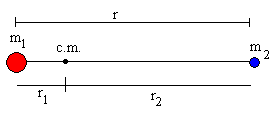
m₁r₁=m₂r₂

r=r₁+r₂

${\displaystyle r_1=\frac{m_{2}r}{m_1+m_2}{r}_2=\frac{m_{1}r}{m_1+m_2}}$

Como el sistema de dos partículas es aislado el centro de masas continuará en reposo en la misma posición.

Si establecemos el origen en el c.m. las ecuaciones del movimiento de los dos cuerpos son

${\displaystyle \begin{array}{l}{m}_1\frac{d^2{r}_1}{d{t}^2}=-G\frac{m_1{m}_2}{r^2}\\ m_2\frac{d^2{r}_2}{d{t}^2}=-G\frac{m_1{m}_2}{r^2}\end{array}}$

Escribiendo r₁ o r₂ en función de r,

${\displaystyle \begin{array}{l}\frac{m_1·m_2}{m_1+m_2}\frac{d^{2}r}{d{t}^2}=-G\frac{m_1·m_2}{r^2}\\ \mu \frac{d^{2}r}{d{t}^2}=-G\frac{m_1·m_2}{r^2}\end{array}}$

El movimiento de las dos cuerpos es equivalente al movimiento de una partícula de masa reducida m , bajo la acción de la fuerza que describe la interacción mutua, la fuerza de atracción entre las dos masas separadas una distancia r=r₁+r₂

Eliminando el producto m₁·m₂

${\displaystyle \frac{d^{2}r}{d{t}^2}=-G\frac{m_1+m_2}{r^2}}$

Supongamos que la separación inicial entre los dos cuerpos es r₀. Definimos las variables adimensionales

x=r/r₀,
τ=t/P

Siendo P el periodo del movimiento circular cuando ambos cuerpos están separados una distancia r₀.

${\displaystyle P^2=\frac{4{\pi }^2{r}_0^3}{G(m_1+m_2)}}$

La ecuación del movimiento se transforma en otra más simple.

${\displaystyle \frac{r_0}{P^2}\frac{d^{2}x}{d{\tau }^2}=-\frac{G(m_1+m_2)}{r_0^2·x^2}\frac{d^{2}x}{d{\tau }^2}=-\frac{4{\pi }^2}{x^2}}$

Integramos esta ecuación diferencial con las condiciones iniciales τ=0, x=1, v=dx/dτ=0.

Transformamos la ecuación diferencial de segundo orden en una de primer orden.

${\displaystyle \frac{d^{2}x}{d{\tau }^2}=\frac{dv}{d\tau }=\frac{dv}{dx}\frac{dx}{d\tau }=v\frac{dv}{dx}=-\frac{4{\pi }^2}{x^2}}$

Obtenemos la velocidad v relativa de un cuerpo respecto del otro integrando la ecuación diferencial de primer orden con la condición inicial x=1, v=0

${\displaystyle {\displaystyle \underset{0}{\overset{v}{\int }}v·dv}=-4{\pi }^2{\displaystyle \underset{1}{\overset{x}{\int }}\frac{dx}{x^2}}\frac{v^2}{2}=4{\pi }^2\left(\frac{1}{x}-1\right)}$

Cuando los cuerpos caen, x disminuye con τ, la velocidad v es negativa. Tenemos que integrar la ecuación diferencial de primer orden

${\displaystyle \frac{dx}{d\tau }=-2\sqrt{2}\pi \sqrt{\frac{1-x}{x}}}$

con las condiciones iniciales τ=0, x=1.

${\displaystyle {\displaystyle \underset{1}{\overset{x}{\int }}\sqrt{\frac{x}{1-x}}}dx=-2\sqrt{2}\pi {\displaystyle \underset{0}{\overset{\tau }{\int }}d\tau }}$

La integral del miembro izquierdo se resuelve haciendo la sustitución

${\displaystyle z^2=\frac{x}{1-x}dx=\frac{2z}{{(1+z^2)}^2}dz}$

Se integra por partes

${\displaystyle \begin{array}{l}{\displaystyle \int \sqrt{\frac{x}{1-x}}dx}={\displaystyle \int \frac{2z^2}{{\left(1+z^2\right)}^2}}dz=,\{\begin{array}{l}u=z,du=dz\\ dv=\frac{2z}{{\left(1+z^2\right)}^2}dz,v=\frac{-1}{1+z^2}\end{array}\\ \frac{-z}{1+z^2}+{\displaystyle \int \frac{dz}{1+z^2}}=\frac{-z}{1+z^2}+\arctan z=-\sqrt{x(1-x)}+\arctan \sqrt{\frac{x}{1-x}}\end{array}}$

Evaluando el integrando para el límite superior e inferior, despejamos el tiempo adimensional τ.

${\displaystyle \tau =\frac{1}{2\sqrt{2}\pi }\left(\sqrt{x-x^2}-\arctan \sqrt{\frac{x}{1-x}}+\frac{\pi }{2}\right)}$

Tenemos una ecuación implícita τ=f(x), dado el valor de x calculamos el tiempo τ. Representamos la función implícita τ=f(x) en el intervalo 0<x<1

f=@(x) (sqrt(x-x.^2)-atan(sqrt(x./(1-x)))+pi/2)/(2*sqrt(2)*pi);
fplot(f,[0,1])
grid on
ylabel('\tau')
xlabel('x')
title('Atracción entre los cuerpos')
view([90 -90]) %gira los ejes

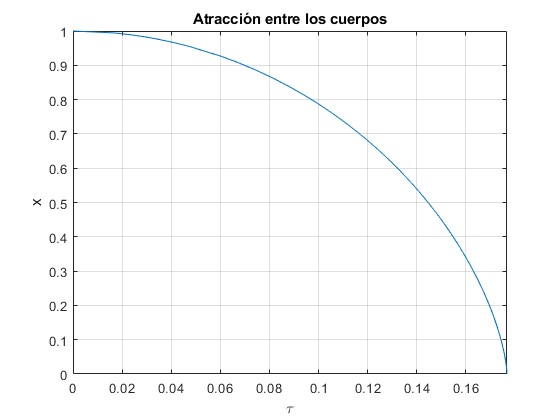
Para x=0, el tiempo τ=0.177

Ejemplo 1:

Sea el sistema formado por la Tierra y el Sol. Supongamos que la Tierra se detiene cuando está a una distancia de una unidad astronómica r₀=1.49·10¹¹ m del centro del Sol.

La posición inicial del Sol y de la Tierra respecto del origen situado en el c.m. es

${\displaystyle r_1=\frac{5.98·{10}^{24}}{5.98·{10}^{24}+1.98·{10}^{30}}1.49·{10}^{11}=4.5·{10}^5\text{m}}$

a la izquierda del c.m.

r₂=1.49·10¹¹-4.5·10⁵=1.49·10¹¹ m

a la derecha del c.m.

El centro de masas del sistema formado por la Tierra y el Sol está muy cerca del centro del Sol que permanecerá prácticamente inmóvil dada su gran diferencia de masa con respecto de la Tierra.

Supongamos que la Tierra cae hacia el Sol, entra en contacto con el Sol, cuando la separación entre sus centros es r=6.96·10⁸+6.37·10⁶ m.

La Tierra está en reposo cuando su distancia del centro del Sol es x=1, y entra en contacto con el Sol cuando su separación es x=r/r₀=0.0047.

Calculamos el valor del tiempo adimensional τ=0.177.

Calculamos el periodo P de la órbita circular de la Tierra alrededor del Sol.

${\displaystyle P=2\pi \sqrt{\frac{{(1.49·{10}^{11})}^3}{6.67·{10}^{-11}(1.98·{10}^{30}+5.98·{10}^{24})}}=31445832\text{s}=\text{364}\text{días}}$

El instante en el que entran en contacto el Sol y la Tierra es t= τ·P=5558126 s=64 días.

Los centros de ambos cuerpos celestes coinciden r=0, ó x=0 en el instante

${\displaystyle t=P\frac{1}{4\sqrt{2}}=5558890\text{s}}$

Ejemplo 2:

La distancia entre los centros de la Tierra y de la Luna es 3.84·10⁸ m

La posición de la Tierra y la Luna respecto del origen situado en el c.m. cuando su separación es r=x·3.84·10⁸ m es

${\displaystyle r_1=\frac{7.34·{10}^{22}}{5.98·{10}^{24}+7.34·{10}^{22}}3.84·{10}^8·x}$

a la izquierda del c.m.

r₂=3.84·10⁸-r₁m

a la derecha del c.m.

El periodo P de la órbita circular de la Luna y de la Tierra alrededor de su c.m. común es

${\displaystyle P=2\pi \sqrt{\frac{{(3.84·{10}^8)}^3}{6.67·{10}^{-11}(7.34·{10}^{22}+5.98·{10}^{24})}}=2352958\text{s}=27\text{días}}$

Si se detiene la Tierra y la Luna cuando su distancia es r₀=3.84·10⁸ m o x=1. Sus centros coinciden r=0, ó x=0, en el instante t

${\displaystyle t=P\frac{1}{4\sqrt{2}}=415948\text{s}=5\text{días}}$

Un problema sencillo de tres cuerpos

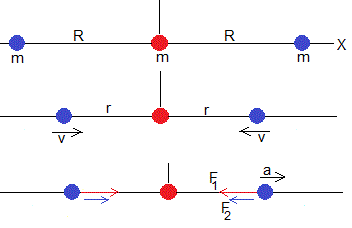
Sean tres partículas de masa m, separadas una distancia R inicialmente

La partícula central (de color rojo) permanece en reposo en el origen. Las otras dos (de color azul) son atraídas hacia el centro por dos fuerzas

${\displaystyle F_1=G\frac{m^2}{r^2},F_2=G\frac{m^2}{4r^2}}$

la fuerza de atracción de la partícula central, situada a una distancia r y la atracción de la otra partícula situada a una distancia 2r

La ecuación del movimiento de la partícula (de color azul) es

${\displaystyle \begin{array}{l}m\frac{d^{2}r}{d{t}^2}=-G\frac{m^2}{r^2}-G\frac{m^2}{4r^2}\\ \frac{d^{2}r}{d{t}^2}=-G\frac{5m}{4r^2}\end{array}}$

Conservación de la energía

La energía del inicial del sistema de tres partículas en resposo es

${\displaystyle U=-2G\frac{m^2}{R}-G\frac{m^2}{2R}=-\frac{5}{2}G\frac{m^2}{R}}$

En el instante t la separación ha disminuido a r. La energía del sistema es

${\displaystyle U=2\left(\frac{1}{2}m{v}^2\right)-2G\frac{m^2}{r}-G\frac{m^2}{2r}=m{v}^2-\frac{5}{2}G\frac{m^2}{r}}$

Aplicando el principio de conservación de la energía

${\displaystyle \begin{array}{l}-\frac{5}{2}G\frac{m^2}{R}=m{v}^2-\frac{5}{2}G\frac{m^2}{r}\\ \frac{dr}{dt}=-\sqrt{\frac{5Gm}{2}}\sqrt{\frac{1}{R}-\frac{1}{r}}\end{array}}$

Se toma la raíz (-) por que r disminuye con el tiempo t, dr/dt<0

Integramos esta ecuación diferencial por separación de variables

${\displaystyle {\displaystyle \underset{R}{\overset{r}{\int }}\sqrt{\frac{r}{R-r}}}dr=-\sqrt{\frac{5Gm}{2R}}{\displaystyle \underset{0}{\overset{t}{\int }}dt}}$

Hacemos el cambio de variable r=Rx. Esta integral la hemos resuelto en el apartado anterior

${\displaystyle R{\displaystyle \int \sqrt{\frac{x}{1-x}}dx}=R\left(-\sqrt{x(1-x)}+\arctan \sqrt{\frac{x}{1-x}}\right)}$

Obtenemos una ecuación implícita t(r)

${\displaystyle \begin{array}{l}{-\sqrt{r(R-r)}+R·\arctan \sqrt{\frac{r}{R-r}}|}_R^r=-\sqrt{\frac{5Gm}{2R}}t\\ \sqrt{r(R-r)}-R·\arctan \sqrt{\frac{r}{R-r}}+R\frac{\pi }{2}=\sqrt{\frac{5Gm}{2R}}t\end{array}}$

Las partículas (de color azul) chocan con la partícula central (de color rojo) r=0, en el instante tal que

${\displaystyle R\frac{\pi }{2}=\sqrt{\frac{5Gm}{2R}}t}$

>> syms x;
>> int(sqrt(x/(1-x)),x,1,0)
ans =-pi/2

Referencias

Para el último apartado, 'Un problema sencillo de tres cuerpos'

Lee H. McDonald, Kirk T. McDonald A Simple 3-Body Gravitational Problem. August 2023