Posición, velocidad y aceleración en coordenadas polares

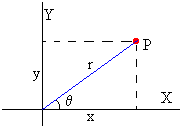
La posición de una partícula es (x, y) en coordenadas rectangulares y (r, θ) en coordenadas polares. La relación es

x=r·cosθ, x=r·sinθ

Expresamos la velocidad de la partícula en coordenadas polares

${\displaystyle \overrightarrow{v}=\frac{d\overrightarrow{r}}{dt}=\widehat{r}\frac{dr}{dt}+r\frac{d\widehat{r}}{dt}}$

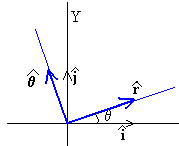
Calculamos las componentes rectangulares de los vectores unitarios

${\displaystyle \begin{array}{l}\widehat{r}=\widehat{i}\cos \theta +\widehat{j}\sin \theta \hfill \\ \widehat{\theta }=-\widehat{i}\sin \theta +\widehat{j}\cos \theta \hfill \end{array}}$

Derivamos con respecto del tiempo

${\displaystyle \begin{array}{l}\frac{d\widehat{r}}{dt}=(-\widehat{i}\sin \theta +\widehat{j}\cos \theta )\frac{d\theta }{dt}=\widehat{\theta }\frac{d\theta }{dt}\hfill \\ \frac{d\widehat{\theta }}{dt}=(-\widehat{i}\cos \theta -\widehat{j}\sin \theta )\frac{d\theta }{dt}=-\widehat{r}\frac{d\theta }{dt}\hfill \end{array}}$

La expresión del vector velocidad en coordenadas polares es

${\displaystyle \overrightarrow{v}=\frac{dr}{dt}\widehat{r}+r\frac{d\theta }{dt}\widehat{\theta }}$

Derivando el vector velocidad con respecto del tiempo, obtenemos el vector aceleración

${\displaystyle \begin{array}{l}\overrightarrow{a}=\frac{d\overrightarrow{v}}{dt}=\frac{d^{2}r}{d{t}^2}\widehat{r}+\frac{dr}{dt}\frac{d\widehat{r}}{dt}+\left(r\frac{d^2\theta }{d{t}^2}+\frac{dr}{dt}\frac{d\theta }{dt}\right)\widehat{\theta }+r\frac{d\theta }{dt}\frac{d\widehat{\theta }}{dt}=\hfill \\ \frac{d^{2}r}{d{t}^2}\widehat{r}+\frac{dr}{dt}\frac{d\theta }{dt}\widehat{\theta }+\left(r\frac{d^2\theta }{d{t}^2}+\frac{dr}{dt}\frac{d\theta }{dt}\right)\widehat{\theta }-r{\left(\frac{d\theta }{dt}\right)}^2\widehat{r}=\hfill \\ \left(\frac{d^{2}r}{d{t}^2}-r{\left(\frac{d\theta }{dt}\right)}^2\right)\widehat{r}+\left(r\frac{d^2\theta }{d{t}^2}+2\frac{dr}{dt}\frac{d\theta }{dt}\right)\widehat{\theta }\hfill \end{array}}$

Fuerza repulsiva inversamente proporcional al cubo de la distancia

Para deducir la ecuación de la trayectoria seguiremos los mismos pasos que para una fuerza inversamente proporcional al cuadrado de la distancia (última sección al final de la página)

Supongamos una partícula de masa m que se mueve bajo la acción de una fuerza central atractiva F(r)=k/r³. Las ecuaciones del movimiento son

${\displaystyle \begin{array}{l}m\left(\frac{d^{2}r}{d{t}^2}-r{\left(\frac{d\theta }{dt}\right)}^2\right)=\frac{k}{r^3}\hfill \\ m\left(r\frac{d^2\theta }{d{t}^2}+2\frac{d\theta }{dt}\frac{dr}{dt}\right)=0\hfill \end{array}}$

La segunda ecuación nos indica que el momento angular L (expresado en coordenadas polares es constante)

${\displaystyle \frac{d}{dt}\left(m{r}^2\frac{d\theta }{dt}\right)=0L=m{r}^2\frac{d\theta }{dt}=\text{cte}}$

Teniendo en cuenta la constancia del momento angular L, escribimos la ecuación del movimiento en la dirección radial, de la forma

${\displaystyle \frac{d^{2}r}{d{t}^2}-\frac{1}{r^3}\left(\frac{k}{m}+\frac{L^2}{m^2}\right)=0}$

Para calcular la ecuación de la trayectoria, r=r(θ), eliminamos el tiempo t del siguiente modo

${\displaystyle \begin{array}{l}\frac{dr}{dt}=\frac{dr}{d\theta }\frac{d\theta }{dt}=\frac{L}{m{r}^2}\frac{dr}{d\theta }\hfill \\ \frac{d^{2}r}{d{t}^2}=\frac{d}{dt}\left(\frac{L}{m{r}^2}\frac{dr}{d\theta }\right)=\frac{d}{d\theta }\left(\frac{L}{m{r}^2}\frac{dr}{d\theta }\right)\frac{d\theta }{dt}=\frac{L}{m{r}^2}\frac{d}{d\theta }\left(\frac{L}{m{r}^2}\frac{dr}{d\theta }\right)\hfill \\ \frac{d^{2}r}{d{t}^2}=\frac{L^2}{m^2{r}^4}\left(\frac{d^{2}r}{d{\theta }^2}-\frac{2}{r}{\left(\frac{dr}{d\theta }\right)}^2\right)\hfill \end{array}}$

Obtenemos una ecuación en términos de r y de sus derivadas respecto del ángulo θ

${\displaystyle \frac{d^{2}r}{d{\theta }^2}-\frac{2}{r}{\left(\frac{dr}{d\theta }\right)}^2-r\left(1+\frac{mk}{L^2}\right)=0}$

Hacemos el cambio de variable u=1/r

${\displaystyle \begin{array}{l}\frac{dr}{d\theta }=-\frac{1}{u^2}\frac{du}{d\theta }\hfill \\ \frac{d^{2}r}{d{\theta }^2}=\frac{2}{u^3}{\left(\frac{du}{d\theta }\right)}^2-\frac{1}{u^2}\frac{d^{2}u}{d{\theta }^2}\hfill \end{array}}$

La ecuación del movimiento se convierte en

${\displaystyle \frac{d^{2}u}{d{\theta }^2}+\left(1+\frac{mk}{L^2}\right)u=0}$

La solución de la ecuación diferencial es

${\displaystyle \begin{array}{l}u=A\sin (\beta \theta )+B\cos (\beta \theta )\\ \beta =\sqrt{1+\frac{mk}{L^2}}\end{array}}$

Como F(r)=k/r³ es una fuerza conservativa, su energía potencial es E_p(r)=k/(2r²). Recuérdese que

${\displaystyle F(r)=-\frac{d}{dr}{E}_p(r)}$

El momento angular y la energía de la partícula es

${\displaystyle \{\begin{array}{l}L=m{r}^2\frac{d\theta }{dt}\\ E=\frac{1}{2}m{\left(\frac{dr}{dt}\right)}^2+\frac{L^2}{2m{r}^2}+\frac{k}{2r^2}=\frac{1}{2}m{\left(\frac{dr}{dt}\right)}^2+\frac{L^2+mk}{2m{r}^2}\end{array}}$

El segundo término es la energía potencial efectiva, inversamente proporcional al cuadrado de la distancia

fplot(@(x) 1./x.^2, [0.5,4])
E=1.5; %energía 
line([0,4],[E,E],'color','k')
rm=sqrt(1/E); % distancia mínima
line([rm,rm],[0,E],'color','k', 'lineStyle','--')
grid on
xlabel('r')
ylabel('V_{ef}(r)')
title('Energía potencial efectiva')

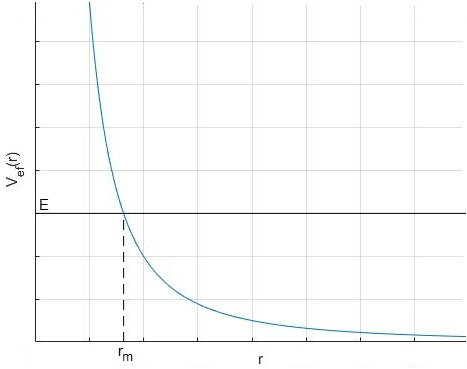
La partícula se acerca hasta una distancia r_m del origen, su componente radial de la velocidad dr/dt=0.

${\displaystyle \begin{array}{l}E=\frac{L^2+mk}{2m{r}_m^2}\\ r_m=\sqrt{\frac{L^2+mk}{2mE}}\end{array}}$

La partícula de energía E, parte del infinito r→∞, u=0, su posición angular θ=0. El coeficiente B deberá ser nulo.

La ecuación de la trayectoria es 1/r=Asin(βθ). El coeficiente A se determina sabiendo que para r→∞, la energía de la partícula es E

Teniendo en cuenta que

${\displaystyle \frac{dr}{dt}=\frac{dr}{d\theta }\frac{d\theta }{dt}=-\frac{\beta }{A}\frac{\cos \left(\beta \theta \right)}{{\sin }^2\left(\beta \theta \right)}\frac{L}{m{r}^2}=-\frac{L}{m}\beta A\cos \left(\beta \theta \right)}$

La energía de la partícula E está relacionada con el coeficiente A

${\displaystyle \begin{array}{l}E=\frac{1}{2}m{\left(\frac{dr}{dt}\right)}^2\\ E=\frac{1}{2}\frac{L^2{\beta }^2}{m}{A}^2\end{array}}$

La ecuación de la trayectoria es

${\displaystyle \frac{1}{r}=\sqrt{\frac{2mE}{L^2+mk}}\sin \left(\sqrt{1+\frac{mk}{L^2}}\theta \right)}$

Dispersión

Una introducción al fenómeno de la dispersión se estudia en la página titulada 'Parámetro de impacto y ángulo de dispersión'

Si v es la velocidad de la partícula cuando r→∞, y b es el parámetro de impacto, la energía E y el momento angular L son

${\displaystyle \begin{array}{l}E=\frac{1}{2}m{v}^2,L=mvb\\ \frac{1}{r}=v\sqrt{\frac{m}{m{b}^2{v}^2+k}}\sin \left(\frac{1}{bv}\sqrt{\frac{m{b}^2{v}^2+k}{m}}\theta \right)\end{array}}$

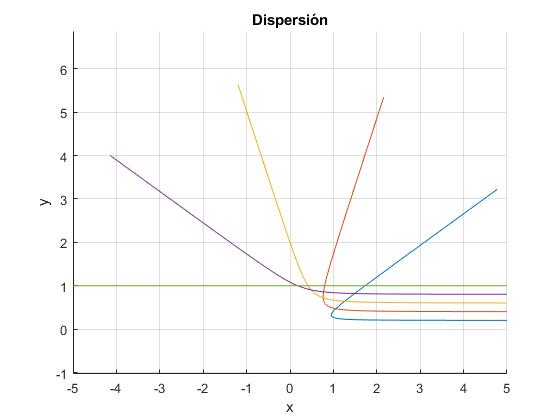
Dibujamos la trayectoria, tomando el término común bajo la raiz igual a la unidad y tomando una velocidad v=1

b=0.8; %parámero de impacto
th=linspace(10,170,40)*pi*b/180;
r=1./sin(th/b);
plot(r.*cos(th),r.*sin(th))
line([0,1],[0,tan(pi*b/2)], 'lineStyle','--', 'color','k') %vectores
line([0,-1],[0,-tan(pi*b)],'color','k')
grid on
axis equal
xlim([-5,5])
xlabel('x')
ylabel('y')
title('Dispersión')

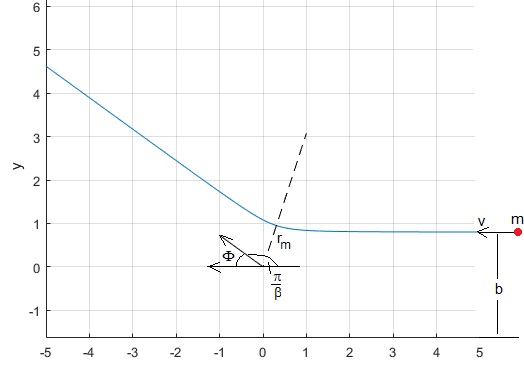
La velocidad inicial y final de la partícula no cambia, cuando r→∞, cambia su dirección. Se define el ángulo de dispersión Φ el que forma la dirección de la velocidad inicial y final de la partícula, tal como se muestra en la figura

Cuando θ→0 y θ→π/β, entonces r→∞. La posición angular de máximo acercamiento es θ=π /(2β)

${\displaystyle \begin{array}{l}\frac{1}{r}=\sqrt{\frac{2mE}{L^2+mk}}\sin \left(\beta \theta \right)\\ \frac{1}{r_m}=\sqrt{\frac{2mE}{L^2+mk}}\sin \left(\beta \frac{\pi }{2\beta }\right)\\ r_m=\sqrt{\frac{L^2+mk}{2mE}}\end{array}}$

coincide con la expresión obtenida anteriormente

La relación entre parámetro de impacto b y el ángulo de dispersión Φ es

${\displaystyle \begin{array}{l}\Phi =\pi -\frac{\pi }{\beta }\\ {\left(1-\frac{\Phi }{\pi }\right)}^2=\frac{m{b}^2{v}^2}{m{b}^2{v}^2+k}\\ b^2=\frac{{\left(\pi -\Phi \right)}^2}{m{v}^2\Phi (2\pi -\Phi )}\end{array}}$

Representamos las trayectorias de las partículas para varios valores del parámetros de impacto b

hold on
for b=0.2:0.2:1 %parámero de impacto
    th=linspace(10,170,100)*pi*b/180;
    r=1./sin(th/b);
    plot(r.*cos(th),r.*sin(th))
end
hold off
grid on
axis equal
xlim([-5,5])
xlabel('x')
ylabel('y')
title('Dispersión')

Fuerza atractiva inversamente proporcional al cubo de la distancia

Como F(r)=-k/r³ es una fuerza conservativa, su energía potencial es E_p(r)=-k/(2r²).

${\displaystyle \{\begin{array}{l}L=m{r}^2\frac{d\theta }{dt}\\ E=\frac{1}{2}m{\left(\frac{dr}{dt}\right)}^2+\frac{L^2}{2m{r}^2}-\frac{k}{2r^2}=\frac{1}{2}m{\left(\frac{dr}{dt}\right)}^2+\frac{L^2-mk}{2m{r}^2}\end{array}}$

El segundo término es la energía potencial efectiva, inversamente proporcional al cuadrado de la distancia

Se pueden dar tres casos

hold on
fplot(@(x) 1./x.^2, [0.5,4])
fplot(@(x) -1./x.^2, [0.5,4])
line([0,4],[0,0])
E=1.5; %energía 
line([0,4],[E,E],'color','k')
rm=sqrt(1/E); % distancia mínima
line([rm,rm],[0,E],'color','k', 'lineStyle','--')
line([0,4],[-E,-E],'color','k')
line([rm,rm],[0,-E],'color','k', 'lineStyle','--')
hold off
grid on
xlabel('r')
ylabel('V_{ef}(r)')
title('Energía potencial efectiva')

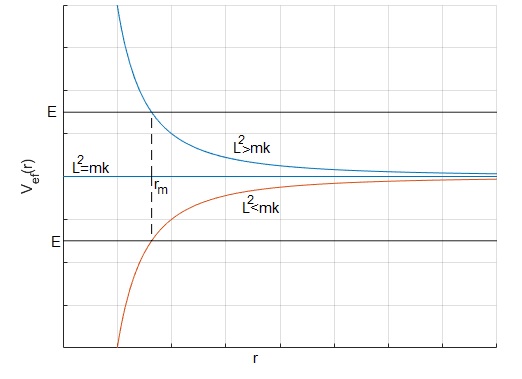
• En el primer caso, L²>mk, cuando E>0, la distancia de la partícula al origen r puede variar desde r_m hasta ∞
• En el tercer caso, L²<mk, cuando E<0, la distancia de la partícula al origen r puede variar desde 0 hasta r_m

La ecuación del movimientos es la misma que en el apartado anterior sustituyendo k por -k

${\displaystyle \frac{d^{2}u}{d{\theta }^2}+\left(1-\frac{mk}{L^2}\right)u=0}$

Examinamos los distintos casos

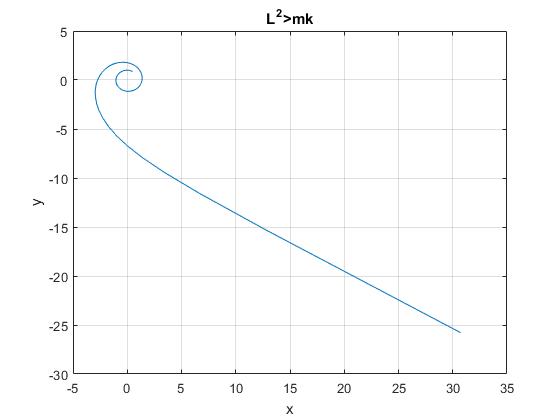
L²>mk

La solución de la ecuación diferencial es la misma que en el apartado anterior sustituyendo k por -k

${\displaystyle \begin{array}{l}u=A\sin (\beta \theta )+B\cos (\beta \theta )\\ \beta =\sqrt{1-\frac{mk}{L^2}}\end{array}}$

Otra forma alternativa es

${\displaystyle u=C\cos \left(\beta (\theta -{\theta }_0)\right)}$

Calculamos la constante C a partir de la conservación de la energía

La energía de la partícula en coordenadas polares es

${\displaystyle \begin{array}{l}E=\frac{1}{2}m\left\{{\left(\frac{dr}{dt}\right)}^2+r^2{\left(\frac{d\theta }{dt}\right)}^2\right\}-\frac{k}{2r^2}\\ E=\frac{1}{2}\frac{L^2}{m{r}^4}\left\{{\left(\frac{dr}{d\theta }\right)}^2+r^2\right\}-\frac{k}{2r^2}\\ E=\frac{1}{2}\frac{L^2}{m}{u}^4\left\{\frac{1}{u^4}{\left(\frac{du}{d\theta }\right)}^2+\frac{1}{u^2}\right\}-\frac{k}{2}{u}^2\\ E=\frac{1}{2}\left\{\frac{L^2}{m}{\left(\frac{du}{d\theta }\right)}^2+\left(\frac{L^2}{m}-k\right)u^2\right\}\end{array}}$

Conocido u y du/dθ, obtenemos la energía E y despejamos la constante C

${\displaystyle C^2=\frac{2mE}{{\beta }^2{L}^2}}$

Para que C sea real, E>0

Cuando r→∞, u→0, β(θ-θ₀)=π/2, θ=π/(2β)+θ₀

beta=1/7;
th_0=pi/3;
th=th_0:pi/18:th_0+pi/(2*beta)-pi/18;
r=1./cos(beta*(th-th_0));
plot(r.*cos(th),r.*sin(th))
grid on
xlabel('x')
ylabel('y')
title('L^2>mk')

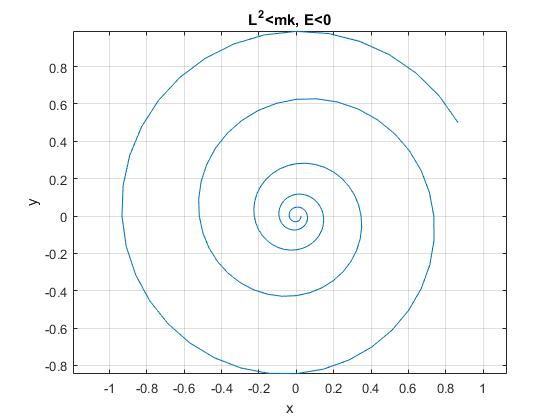
L²<mk

La solución de la ecuación diferencial en u es

${\displaystyle \begin{array}{l}u=A\exp (\beta \theta )+B\exp (-\beta \theta )\\ \beta =\sqrt{\frac{mk}{L^2}-1}\end{array}}$

Conocido u y du/dθ, obtenemos la energía E de la partícula

${\displaystyle \begin{array}{l}E=\frac{1}{2m}\left(mk-L^2\right)\left(-4AB\right)\\ AB=-\frac{mE}{2{\beta }^2{L}^2}\end{array}}$

E<0

De forma alternativa

${\displaystyle u=C\cosh \beta (\theta -{\theta }_0)}$

Conocido u y du/dθ, obtenemos la energía E de la partícula y despejamos la constante C como en el apartado anterior

${\displaystyle C=\sqrt{\frac{-2mE}{{\beta }^2{L}^2}}}$

Para que C sea real, E<0. Como la función |cosh(x)|≥1, la trayectoria r=1/u está limitada

beta=1/7;
th_0=pi/6;
th=th_0:pi/18:10*pi;
r=1./cosh(beta*(th-th_0));
plot(r.*cos(th),r.*sin(th))
grid on
axis equal
xlabel('x')
ylabel('y')
title('L^2<mk, E<0')

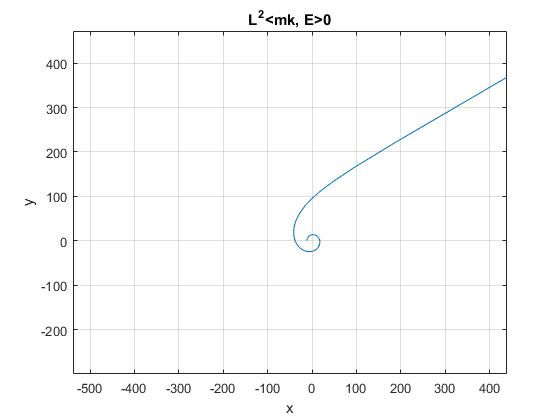
E>0

De forma alternativa

${\displaystyle u=C\sinh \beta (\theta -{\theta }_0)}$

Conocido u y du/dθ, obtenemos la energía E de la partícula y despejamos la constante C como en el apartado anterior

${\displaystyle C=\sqrt{\frac{2mE}{{\beta }^2{L}^2}}}$

Para que C sea real E>0. r tiende a infinito cuando sinh se hace cero, una trayectoria ilimitada

beta=1/100;
th_0=pi/6;
th=3*pi:-pi/18:th_0-pi/18;
r=1./sinh(beta*(th-th_0));
plot(r.*cos(th),r.*sin(th))
grid on
axis equal
xlabel('x')
ylabel('y')
title('L^2<mk, E>0')

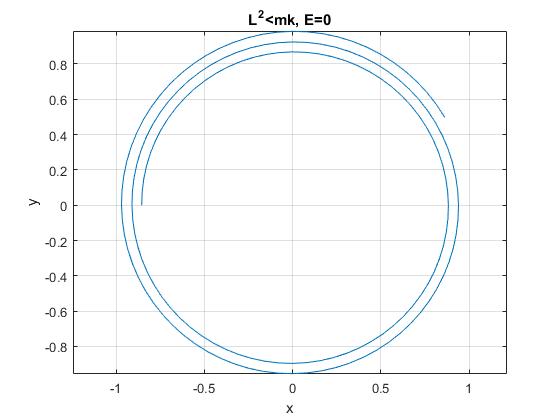
E=0

Cuando E=0, A o B es cero

u=Aexp(βθ) o bien, u=Aexp(-βθ)

beta=1/100;
th_0=pi/6;
th=th_0:pi/36:5*pi;
r=1./exp(beta*th);
plot(r.*cos(th),r.*sin(th))
grid on
axis equal
xlabel('x')
ylabel('y')
title('L^2<mk, E=0')

L²=mk

La ecuación diferencial en u se reduce a

${\displaystyle \begin{array}{l}\frac{d^{2}u}{d{\theta }^2}=0\\ u=A\theta +B\end{array}}$

E>0

Conocido u y du/dθ, obtenemos la energía E de la partícula y despejamos la constante A como en el apartado anterior

${\displaystyle \begin{array}{l}E=\frac{1}{2}\frac{L^2}{m}{A}^2\\ A=\sqrt{\frac{2mE}{L^2}}\end{array}}$

th_0=pi/6;
th=th_0:pi/18:5*pi;
r=1./(th+pi);
plot(r.*cos(th),r.*sin(th))
grid on
axis equal
xlabel('x')
ylabel('y')
title('L^2=mk, E>0')

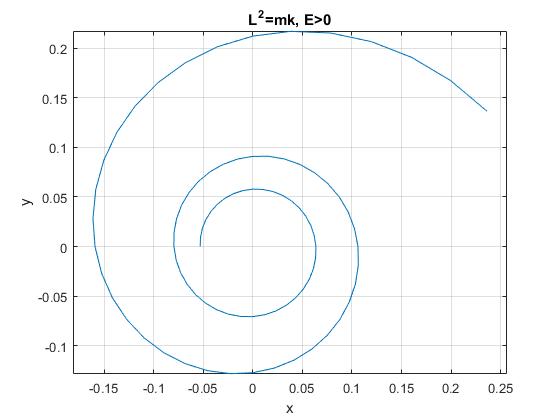
u=0, r=∞, para el ángulo θ=-B/A

E=0

Cuando E=0, el coeficiente A=0, y u=B o r=1/B. La trayectoria es una circunferencia

Referencias

O.L. de Lange, J. Pierrus. Solved Problems in Classical Mechanics. Analytical and numerical solutions with comments. Oxford University Press (2010). Questions 8.11

Douglas Cline. Variational Principles in Classical Mechanics. Second edition, 2019, pp. 273