Interpolación lineal

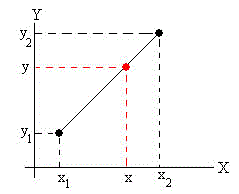
Hay varios métodos de interpolar datos, el más simple es la interpolación lineal, que entenderemos con el siguiente esquema:

Conocemos los datos de (x₁, y₁) y de (x₂, y₂) y queremos conocer el valor desconocido de y cuando se porporciona la abscisa x₁<x<x₂. Si suponemos que los puntos 1 y 2 están unidos por una recta, calculamos fácilmente el valor de y mediante la siguiente relación

${\displaystyle y=y_1+\frac{y_2-y_1}{x_2-x_1}(x-x_1)}$

Este procedimiento se denomina interpolación lineal. MATLAB dispone para este propósito de la función interp1. Creamos un script y seleccionamos el procedimiento por defecto linear

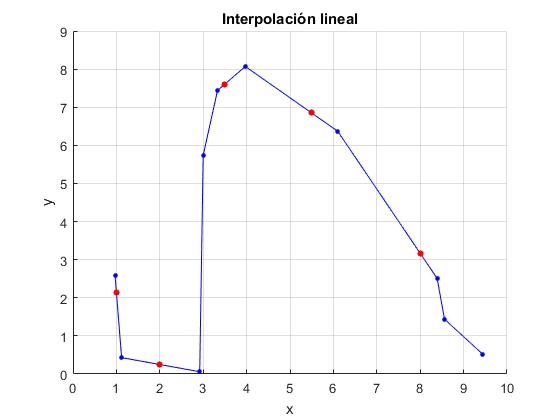
x=[0.97 1.12 2.92 3.00 3.33 3.97 6.10 8.39 8.56 9.44];
y=[2.58 0.43 0.06 5.74 7.44 8.07 6.37 2.51 1.44 0.52];
xx=[1.0 2.0 3.5 5.5 8.0];
yy=interp1(x,y,xx,'linear');
disp([xx' yy'])

Corremos el script en la ventana de comandos

    1.0000    2.1500
    2.0000    0.2491
    3.5000    7.6073
    5.5000    6.8489
    8.0000    3.1674

Completamos el script para incluir la representación gráfica de los datos (color azul) y los interpolados linealmente (color rojo)

x=[0.97 1.12 2.92 3.00 3.33 3.97 6.10 8.39 8.56 9.44];
y=[2.58 0.43 0.06 5.74 7.44 8.07 6.37 2.51 1.44 0.52];
xx=[1.0 2.0 3.5 5.5 8.0];
yy=interp1(x,y,xx,'linear');
disp([xx' yy'])
hold on
plot(x,y,'-bo','markersize',3,'markerfacecolor','b')
plot(xx,yy,'ro','markersize',4,'markerfacecolor','r')
xlabel('x')
ylabel('y')
grid on
title('Interpolación lineal');
hold off

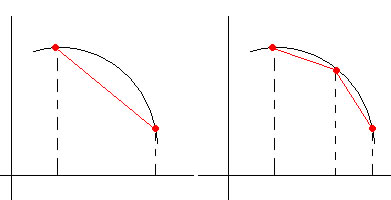
Con la interpolación lineal hay que ser cuidadoso. En la figura de la izquierda tenemos la aproximación lineal (en rojo) de una función (en negro) que es muy pobre ya que los puntos están muy separados. Añadiendo un punto intermedio, mejora la aproximación lineal.

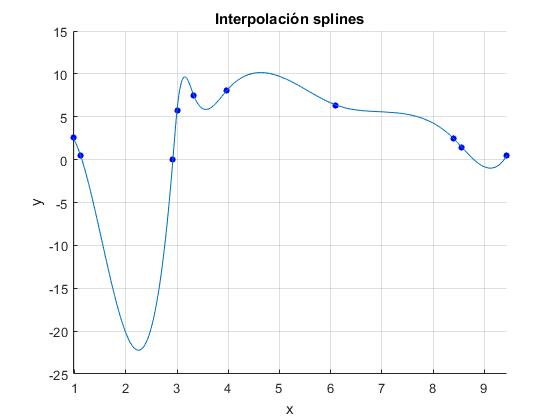
Splines

Es un procedimiento de interpolación que produce muy buenos resultados.

x=[0.97 1.12 2.92 3.00 3.33 3.97 6.10 8.39 8.56 9.44];
y=[2.58 0.43 0.06 5.74 7.44 8.07 6.37 2.51 1.44 0.52];
hold on
plot(x,y,'bo','markersize',4,'markerfacecolor','b')

z=@(xx) interp1(x,y,xx,'spline');
fplot(z,[x(1),x(end)])
hold off
xlabel('x')
ylabel('y')
grid on
title('Interpolación splines')

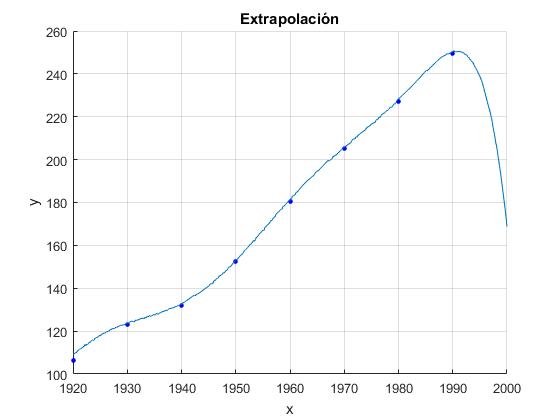
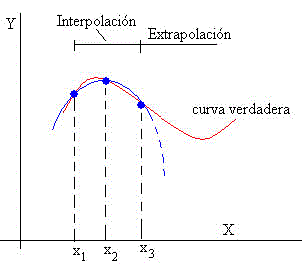
Extrapolación

Es la estimación de un valor de x, que está fuera del intervalo de datos. En el ejemplo anterior, si x está comprendido en el intervalo 0.97<x<9.44 se dice que es interpolación y si x<0.97 ó x>9.44 se dice que es extrapolación.

El ejemplo más significativo es la predicción de la población de Estados Unidos en el año 2000, conocido los censos en los siguientes años (millones de habitantes)

x=[1920 1930 1940 1950 1960 1970 1980 1990];
y=[106.46 123.08 132.12 152.27 180.67 205.05 227.23 249.46];
n=length(x); %número de pares de datos
p=polyfit(x,y,n-1);
%A=vander(x);
%p=A\y' %sistema de ecuaciones lineales, y' es vector columna
z=@(xx) polyval(p,xx);

fprintf('Población en el año 2000, %3.2f\n',polyval(p,2000))
hold on
plot(x,y,'bo','markersize',3,'markerfacecolor','b')
fplot(z,[1920,2000])
xlabel('x')
ylabel('y')
grid on
title('Extrapolación');
hold off

Aparece un aviso en la ventana de comandos, al llamar a la función polyfit para calcular los coeficientes del polinomio. En la página anterior, elaboramos una alternativa (dos líneas comentadas %) para evitar el aviso. Véase 'Interpolación de Lagrange'

Warning: Polynomial is badly conditioned. Add points with distinct X values, 
reduce the degree of the polynomial, or try centering and scaling as described 
in HELP POLYFIT. 
> In polyfit (line 75)
  In xxx (line 4) 
Población en el año 2000, 168.81

La población de Estados Unidos estimada para el año 2000 era de 195.77 millones de habitantes, en contraste con la población real ese año de 281.42 millones. Una diferencia significativa, por lo que hemos de tener cuidado con el procedimiento de extrapolación.