Periodos y alturas

Para explicar el concepto de altura y periodo de las olas ensayamos con una serie pequeña de datos.

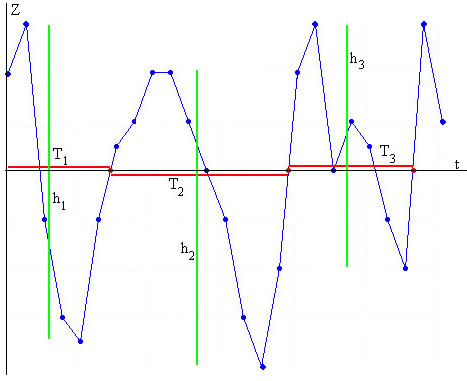
Supongamos que hemos tomado unos pocos datos del desplazamiento z de las olas con una frecuencia de muestreo f_s=2 Hz. Sobre la gráfica marcamos mediante un segmento de color rojo, los periodos T_i, la distancia temporal entre dos ceros alternos y la altura h_i mediante un segmento de color verde, la diferencia entre el valor máximo y mínimo del desplazamiento de la ola durante un periodo.

Para calcular las intersecciones nos fijamos en el siguiente producto elemento a elemento de la serie de datos z=[2,3,-1,-3,-3.5,-1,0.5,1,2,2,1,-1,-3,-4,-2,2,3,0,1,0.5,-1,-2,3,1].

Los cambios de signo del desplazamiento z_i, tienen lugar para los siguientes pares de índices i: 2 y 3, 6 y 7, 11 y 12, 15 y 16, 20 y 21, 22 y 23. El primer elemento del par z_i, tiene un signo y el segundo elemento del par z_i+1 tiene signo contario.

Multiplicamos elemento a elemento dos vectores z(1:end-1) y z(2:end) cuyo resultado vemos en la fila titulada Producto. Marcamos los números negativos y los índices i de estos elementos, que se corresponden con los primeros elementos 2, 6, 11, 15, 20, 22 de los pares de índices anteriormente citados.

>> z=[2,3,-1,-3,-3.5,-1,0.5,1,2,2,1,-1,-3,-4,-2,2,3,0,1,0.5,-1,-2,3,1];
>> p=z(1:end-1).*z(2:end)
p =    6.0000   -3.0000    3.0000   10.5000    3.5000   -0.5000    
0.5000    2.0000    4.0000    2.0000   -1.0000    3.0000   12.0000    
8.0000   -4.0000    6.0000       0         0    0.5000   -0.5000    
2.0000   -6.0000    3.0000
>> find(p<0)
ans =     2     6    11    15    20    22

Con este sencillo código obtenemos los índices de los elementos buscados.

Sin embargo, tenemos un problema si justamente cuando el desplazamiento z cambia de signo insertamos un cero, por ejemplo z=[2,3,-1,-3,-3.5,-1,0.5,1,2,2,1,0,-1,-3,-4,-2,2,3,0,1,0.5,-1,-2,3,1].

>>  z=[2,3,-1,-3,-3.5,-1,0.5,1,2,2,1,0,-1,-3,-4,-2,2,3,0,1,0.5,-1,-2,3,1];
>> p=z(1:end-1).*z(2:end)
>>  find(p<0)
ans =     2     6    16    21    23

No aparece el índice 10 ó 11 donde hay un cambio de signo de 1 a 0 o bien, de 0 a -1. Para soluccionar este problema se añaden las siguientes líneas de código

z=[2,3,-1,-3,-3.5,-1,0.5,1,2,2,1,0,-1,-3,-4,-2,2,3,0,1,0.5,-1,-2,3,1];
d0=z(z~=0);
b0=1:length(z);
b0=b0(z~=0);
f=find(d0(1:end-1).*d0(2:end)<0);
cero=b0(f)

En la ventana de comandos obtenemos la respuesta correcta

cero =     2     6    11    16    21    23

El difícil que se presente este caso, ya que a los valores originales de las medidas de los desplazamientos hay que restarles el valor medio y crear un nuevo vector z_i cuyo valor medio sea cero, parece difícil encontrar valores cero del desplazamiento justamente en el límite entre dos bloque de datos de distinto signo.

Dado que las medidas de los desplazamientos z, se toman a intervalos de tiempo constante Δt=1/f_s. El vector de tiempos se obtiene a patir de la frecuencia f_s del siguiente modo:

>> Fs=2;
>> t=(0:length(z)-1)/Fs
t =         0    0.5000    1.0000    1.5000    2.0000    2.5000    
3.0000    3.5000    4.0000     4.5000    5.0000    5.5000    6.0000    
6.5000    7.0000    7.5000    8.0000    8.5000     9.0000    9.5000   
10.0000   10.5000   11.0000   11.5000   12.0000

Periodos

Un periodo comprende dos bloques de datos consecutivos z_i de signos contrarios. Por ejemplo, el periodo marcado como T₁, comienza en t=0 y termina en el segundo cruce de z con el eje de los tiempos, entre los índices 6 y 7. El periodo marcado como T₂ empieza al final del arterior y termina en el cuarto cruce con el eje de los tiempos, entre los índices 16 y 17, y así sucesivamente. Tomamos los valores del vector cero de dos en dos.

>>cero=cero(2:2:end);
cero =     6    16    23

Para calcular de forma precisa los periodos T₁, T₂, T₃, .... realizamos un proceso de interpolación tal como se puede apreciar en la figura anterior y en ésta.

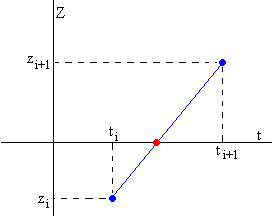
Calculamos la ecuación de la recta que pasa por los dos puntos cuyas ordenadas z_i y z_i+1 tengan signos contarios y su intersección con el eje horizontal, la abscisa t del punto de color rojo.

${\displaystyle \begin{array}{l}z=\frac{\left(z_{i+1}-z_i\right)t+z_i{t}_{i+1}-z_{i+1}{t}_i}{t_{i+1}-t_i}\\ z=0t=\frac{z_{i+1}{t}_i-z_i{t}_{i+1}}{t_{i+1}-t_i}\end{array}}$

>> T=(z(cero+1).*t(cero)-z(cero).*t(cero+1))./(z(cero+1)-z(cero));
>> T=[0,T];
>> periodos=diff(T)
periodos =    2.8333    4.9167    3.4500 

que son los valores de los periodos T₁, T₂ y T₃ señalados en la primera figura.

Cuando hay muchos datos tomados en intervalos de tiempo pequeños no parece que haya apenas diferencia estadística significativa entre t_i y el valor t interpolado, por lo que podríamos omitir la primera línea de código y sustituirla la segunda por la siguiente:

>> T=[0,t(cero)];
>> periodos=diff(T)
periodos =    2.5000    5.0000    3.5000

Alturas

La altura de la ola es la diferencia entre el máximo valor y el mínimo valor del desplazamiento z en un periodo T_i. Las alturas están señaladas en la primera figura por segmentos de color verde marcados como h₁, h₂ y h₃.

La porción de código que nos permite calcular las alturas no precisa de explicación adicional

>> altura=zeros(1,length(cero));
>> altura(1)=max(z(1:cero(1)))-min(z(1:cero(1))) 
>> for i=1:length(cero)-1
    altura(i+1)=max(z(cero(i):cero(i+1)))-min(z(cero(i):cero(i+1))) 
end
>> altura =    6.5000    6.0000    5.0000

Unimos los distintos bloques de código para crear la función alturas_periodo que nos calcule y devuelva las alturas y periodos

function [altura,periodos] = alturas_periodos(z,Fs)
    t=(0:length(z)-1)/Fs;

%puntos de corte con el eje de los tiempos
    d0=z(z~=0);
    b0=1:length(z);
    b0=b0(z~=0);
    f=find(d0(1:end-1).*d0(2:end)<0);
    cero=b0(f);

    cero=cero(2:2:end);
%interpolación, cálculo de los periodos
    y2=z(cero+1);
    x2=t(cero+1);
    x1=t(cero);
    y1=z(cero);
    T=(y2.*x1-y1.*x2)./(y2-y1);
    T=[0,T];
    %T=[0,t(cero)];   %alternativa a la interpolación
    periodos=diff(T);

%alturas
    altura=zeros(1,length(cero));
    altura(1)=max(z(1:cero(1)))-min(z(1:cero(1)));
    for i=1:length(cero)-1
        altura(i+1)=max(z(cero(i):cero(i+1)))-min(z(cero(i):cero(i+1)));
    end
end

Probamos la función mediante el siguiente script

z=[2,3,-1,-3,-3.5,-1,0.5,1,2,2,1,0,-1,-3,-4,-2,2,3,0,1,0.5,-1,-2,3,1];
Fs=2;
[h,T]=alturas_periodos(z,Fs);
tt=zeros(1,length(T));
tt(1)=T(1);
for i=2:length(T)
    tt(i)=tt(i-1)+T(i);
end
hold on
t=(0:length(z)-1)/Fs;
plot(t,z,'-o','markersize',4,'markerfacecolor','b');
plot(tt,0,'ro','markersize',4,'markerfacecolor','r');
grid on
hold off
xlabel('Tiempo')
ylabel('Desplazamiento')
title('Alturas y periodos') 

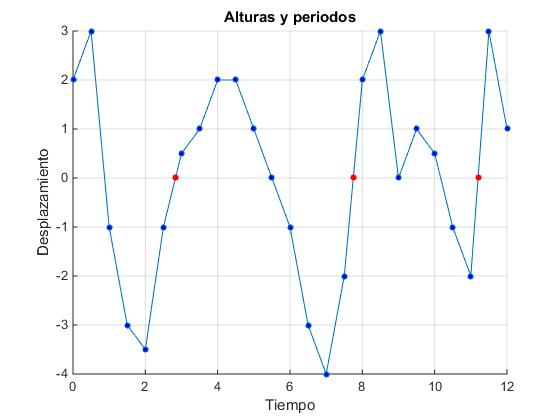
La distancia entre el origen y el primer punto de color rojo es el primer periodo, la distancia entre dos puntos de color rojo consecutivos es un periodo. La altura de las olas en cada periodo es la diferencia entre el máximo y mínimo del desplazamiento z: 6.5, 6 y 5, respectivamente.

En la ventana de comandos obtenemos los valores de las alturas y periodos

>> h
h =    6.5000    6.0000    5.0000
>> T
T =    2.8333    4.9167    3.4500

Una vez que hemos aprendido a calcular las alturas y periodos vamos a analizar estadísticamente el fichero olasZ.txt con los 2304 datos del desplazamiento z tomados durante 30 minutos.

Alturas de las olas

Agrupamos los datos de las alturas en intervalos de anchura 20 cm. La altura de cada barra la calculamos mediante la siguiente fórmula

${\displaystyle p(x_i)=\frac{N_i}{N·\Delta x}}$

Donde N_i es el número de alturas que caben en el intervalo i y Δx=20 cm es la anchura de cada intervalo. N=2304 es el número total de datos.

Ajustamos el diagrama de barras a la función de distribución de Rayleigh

${\displaystyle \begin{array}{l}f(x)=2\frac{x}{H_{rms}^2}\exp \left(-\frac{x^2}{H_{rms}^2}\right)\\ H_{rms}^2=\frac{1}{M}{\displaystyle \sum _{j=1}^M{h}_j^2}\end{array}}$

Es fácil comprobar analíticamente que el área bajo la curva f(x) es la unidad. Utilizamos Math Symbolic para realizar esta comprobación

>> syms a positive;
>> syms x;
>> f=2*x*exp(-x^2/a^2)/a^2;
>> int(f,x,0,inf)
ans =1

La función nlinfit realiza el ajuste de los datos p(x_i) a una función que que depende de un parámetro H_rms. La función nlinfit devuelve el valor del parámetro (en el código af) de la función f(x) que mejor ajusta a los datos. Comprobamos que el valor af es próximo al valor H_rms calculado de forma directa con los datos de las alturas en la fórmula anterior y que se guarda en la variable a0.

load olasZ.txt;
z=olasZ-mean(olasZ);
Fs=1.28;
clear olasZ
%tabla de frecuencias
[h,T]=alturas_periodos(z,Fs);
x=0:20:440;
num=hist(h,x);
frec=num/(sum(num)*20);

%función de Rayleigh y diagrama de frecuencias
f=@(a,x) 2*x.*exp(-x.^2/a^2)/a^2;
a0=sqrt(sum(h.^2)/length(h));  %valor inicial del parámetro a
af=nlinfit(x,frec,f,a0)
xx=linspace(0,max(h),100);
y=f(af,xx);
hold on
bar(x,frec,'c');
plot(xx,y,'r')
xlim([0,max(h)])
xlabel('Alturas')
ylabel('Frecuencia')
title('Ajuste a la función de Rayleigh')
hold off

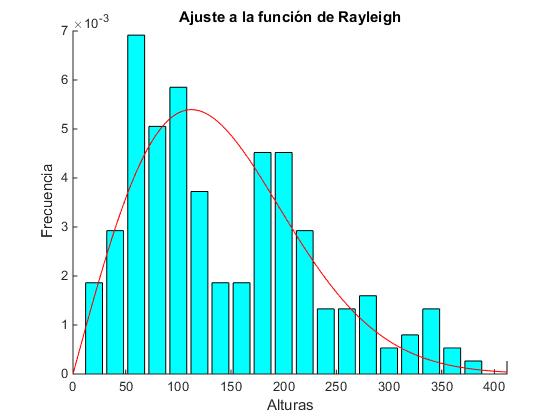
El valor de H_rms es 170.68 calculado mediante los datos de las alturas, el valor devuelto por nlinfit es af=158.96

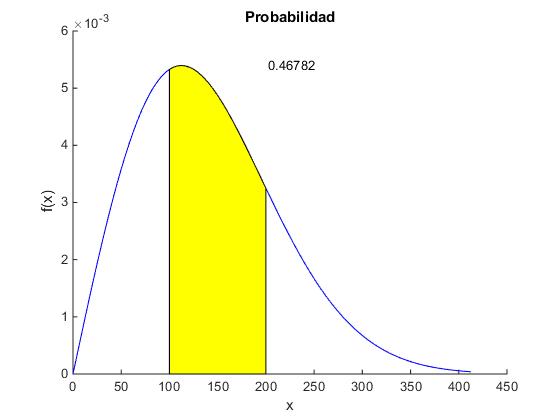
La probabilidad de que las alturas de las olas esté comprendida entre h₀ y h₁ se calcula integrando la función de distribución de Rayleigh f(x)

${\displaystyle {\displaystyle {\int }_{h_0}^{h_1}f(x)dx=}\exp \left(-\frac{h_0^2}{H_{rms}^2}\right)-\exp \left(-\frac{h_1^2}{H_{rms}^2}\right)}$

Cuando h₀=0 y h₁=∞ obtenemos la unidad como área bajo la curva.

Añadimos el siguiente código al script anterior

....
figure
hold on
x=linspace(0,max(h),100);
y=f(af,x);
plot(x,y,'b')
x0=100; x1=200;
xx=[x0 x0 x(x>x0 & x<x1) x1 x1];
yy=[0 f(af,x0) y(x>x0 & x<x1) f(af,x1) 0];
fill(xx,yy,'y');
res=exp(-x0^2/af^2)-exp(-x1^2/af^2);
text(x1+2, max(y),num2str(res));
title('Probabilidad')
xlabel('x')
ylabel('f(x)')
hold off

Ordenamos las alturas h_i en orden descendente con la función sort. La primera es la mayor y la última, es la menor.

El valor medio de las alturas de las olas es

${\displaystyle <h>=\frac{1}{M}{\displaystyle \sum _{i=1}^M{h}_i}}$

La media de 1/3 de las olas de mayor altura es

${\displaystyle <h{>}_{1/3}=\frac{1}{M/3}{\displaystyle \sum _{i=1}^{M/3}{h}_i}}$

La media de 1/10 de las olas de mayor altura

${\displaystyle <h{>}_{1/10}=\frac{1}{M/10}{\displaystyle \sum _{i=1}^{M/3}{h}_i}}$

Importamos el fichero olasZ.txt mediante File/Import Data...

>> z=olasZ-mean(olasZ);
>> [h,T]=alturas_periodos(z,1.28);
>> mean(h)
ans =  146.6330
>> h=sort(h,'descend');
>> h(1)
ans =   412  % más alta
>> h(end)
ans =    11  %menor altura
>> M=length(h)
M =   188     %número de datos de alturas
>> M/3
ans =   62.6667
>> sum(h(1:63))/63  %1/3 de las olas más altas
ans =  249.1587
>> sum(h(1:19))/19  %1/10 de las olas más altas
ans =  323.8947

Periodos de las olas

El periodo medio es

${\displaystyle <T>=\frac{1}{M}{\displaystyle \sum _{i=1}^M{T}_i}}$

La media de 1/3 de los periodos más grandes es

${\displaystyle <T{>}_{1/3}=\frac{1}{M/3}{\displaystyle \sum _{i=1}^{M/3}{T}_i}}$

>> mean(T)
ans =    9.5268
>> T=sort(T,'descend');
>> T(1)
ans =   18.0682 %el periodo más grande
>> T(end)
ans =    1.4508  %el periodo más pequeño
>> sum(T(1:63))/63 %1/3 de los periodos más grandes
ans =   14.5961

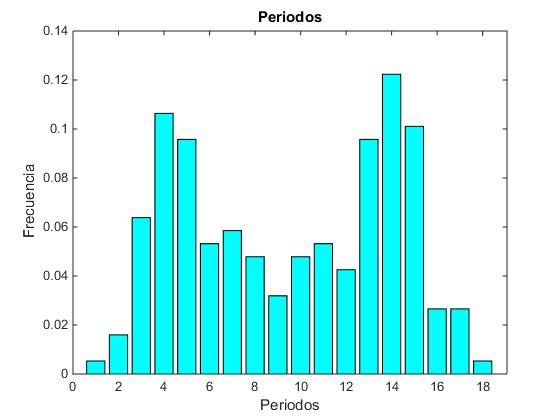
Con los datos relativos a los 188 periodos devueltos por la función alturas_periodos, hacemos una representación gráfica en forma de diagrama de barras centradas en T=1, T=2, T=3... tomando un intervalo de anchura 1 segundo, del mismo modo que se hizo con los desplazamientos z. Añadimos las siguientes líneas de código al script

figure
x=0:max(T);
num=hist(T,x);
frec=num/sum(num);
bar(x,frec,'c');
xlim([0,max(T)+1])
xlabel('Periodos')
ylabel('Frecuencia')
title('Periodos')