Función de distribución de Weibull
Media aritmética y desviación estándar
Si tenemos un conjunto de n números [x1 x2 x3....xn], se define la media aritmética <x>
Si queremos conocer la desviación del conjunto de datos respecto de la media, definimos la desviación estándar σ
MATLAB calcula la media y desviación estándar de un conjunto de datos llamando a las funciones
>> x=[1.65 1.82 1.72 1.75 1.73 1.85 1.90 1.74 1.76 1.77]; >> mean(x) ans=1.7690 >> std(x) ans=0.0713
En ocasiones las velocidades del viento vienen dadas por números enteros, de modo que cada valor entero se mide varias veces durante el periodo de observación. Así, si el dato xi se ha medido wi veces. Tendremos dos vectores x de las medidas y w de las observaciones de dicha medida (pesos) de la misma dimensión m.
x=[x1, x2, x3,....xm]
w=[w1, w2, w3,....wm]
Las fórmulas de la media aritmética y desviación estándar se expresan:
| orden, i | medida, x | observaciones, w |
|---|---|---|
| 1 | 6 | 19 |
| 2 | 7 | 54 |
| 3 | 8 | 42 |
| total, n | 115 |
Definimos dos funciones
Para calcular el valor medio definimos la función
function res=w_media(x,w)
res=sum(w.*x)/sum(w);
end
Para calcular la desviación estándar definimos la función
function res=w_estandar(x,w)
n=sum(w);
media=sum(w.*x)/n;
suma2=sum(w.*(x-media).^2);
res=sqrt(suma2/(n-1));
end
En la ventana de comandos probamos las dos funciones que hemos definido
>> x=[6 7 8]; >> w=[19 54 42]; >> w_media(x,w) ans = 7.2000 >> w_estandar(x,w) ans = 0.7034
Frecuencias
Se define frecuencia f(xi) de una medida xi como el cociente del número wi de observaciones de dicha medida dividida por el número total n de medidas. La frecuencia acumulada F(xi) se define como la suma de las frecuencias desde k=1 a i
La tabla anterior de medidas xi y número de observaciones de cada medida wi la convertimos en tabla de frecuencias f(xi) y frecuencias acumuladas F(xi).
| orden, i | medida, x | observaciones, w | frecuencia, f | frecuencia acumulada, F |
|---|---|---|---|---|
| 1 | 6 | 19 | 0.165 | 0.165 |
| 2 | 7 | 54 | 0.470 | 0.635 |
| 3 | 8 | 42 | 0.365 | 1.0 |
| total, n | 115 | 1.0 |
Modelo estadístico
Es conveniente establecer un modelo de las frecuencias de las velocidades del viento (última figura de la página 'Análisis de los datos del viento') que venga descrito por una función matemática continua en vez de por una tabla de valores discretos.
La función f(x) representa la probabilidad de que la velocidad del viento esté en un intervalo entre x y x+dx. El área bajo f(x) es la unidad.
La probabilidad de que la velocidad del viento esté comprendida entre x0 y x1 viene dada por la integral
Si el número N de medidas de la velocidad del viento es grande y se ha hecho una medida en el intervalo de tiempo Δt (10 minutos, una hora). El tiempo en el que el viento está soplando con una velocidad comprendida entre entre x0 y x1 es N·Δt·P(x0≤x< x1)
El valor medio de la velocidad <x> y la desviación estándar σ tienen ahora la siguiente definición:
La distribución de probabilidad acumulada F(x) se define
Hay varias funciones f(x) que se pueden utilizar para describir la frecuencia de la distribución de velocidades del viento (última figura de la página 'Análisis de los datos del viento'). Las más utilizadas son las funciones de Weibull y Rayleigh.
Función de distribución de Weibull
La función de distribución Weibull depende de dos parámetros denominados c y k y la función de distribución de Rayleigh de un sólo parámetro. Esto hace que la primera sea más versátil y preferida que la segunda por lo que la estableceremos como modelo.
Para dibujar las gráficas de esta función con c=1 y variando el parámetro k, escribimos el script
c=1;
K=[1.2 1.6 2.0 2.4 2.8];
f=@(k,x) (k/c)*((x/c).^(k-1)).*exp(-(x/c).^k);
x=linspace(0,2.5,100);
hold on
for i=1:length(K)
plot(x,f(K(i),x),'displayName',num2str(K(i)))
end
ylim([0 1.2])
xlabel('x')
ylabel('f(x)')
title('Función de Weibull')
legend('-DynamicLegend','location','NorthEast')
hold off
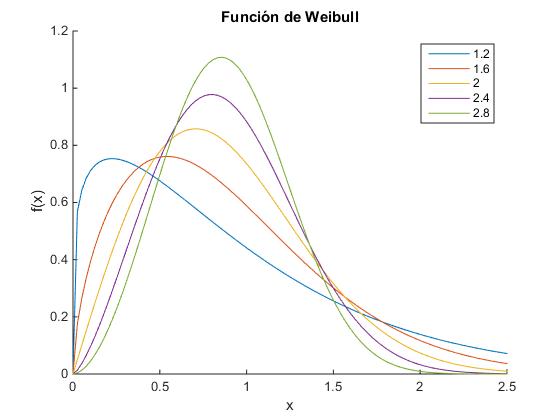
La velocidad para la cual la función de distribución de Weibull alcanza un máximo se obtiene derivando f(x) e igualando a cero.
El valor medio <x>
Donde se ha hecho el cambio de variable y=(x/c)k,
La función gamma Γ(x) se define
Si n es un número entero Γ(n+1) =n! (factorial de n). Para otros valores x la función
Comprobamos en la ventana de comandos que el área bajo la curva de cualquiera de las gráficas es la unidad, y que el valor medio <x>=c·Γ(1+1/k)
>> k=2.8;c=1; >> f=@(x) (k/c)*((x/c).^(k-1)).*exp(-(x/c).^k); >> quad(f,0,3) %area bajo la curva f(x) ans = 1.0000 >> g=@(x) x.*f(x); >> quad(g,0,3) %valor medio ans = 0.8905 >> c*gamma(1+1/k) %valor medio ans = 0.8905
La desvación estándar σ
Otros resultados interesantes son los siguientes:
- La probabilidad de que la velocidad del viento x sea mayor o igual que x0
- La probabilidad de que la velocidad del viento x este en el intervalo comprendido entre x0 y x1.
Representamos f(x) y calculamos la probabilidad P(x) en el intervalo (0.75, 1.25), es decir, centrado en x=1 y de anchura 0.5
k=2.8;c=1;
f=@(x) (k/c)*((x/c).^(k-1)).*exp(-(x/c).^k);
x=linspace(0,3,100);
y=f(x);
hold on
plot(x,y,'r')
x0=0.75;x1=1.25;
xx=[x0 x0 x(x>x0 & x<x1) x1 x1];
yy=[0 f(x0) y(x>x0 & x<x1) f(x1) 0];
fill(xx,yy,'y');
res=quad(f,x0,x1)
prob=exp(-(x0/c)^k)-exp(-(x1/c)^k)
text(1.5, max(y)-0.1,num2str(res));
title('Probabilidad')
xlabel('x')
ylabel('f(x)')
hold off
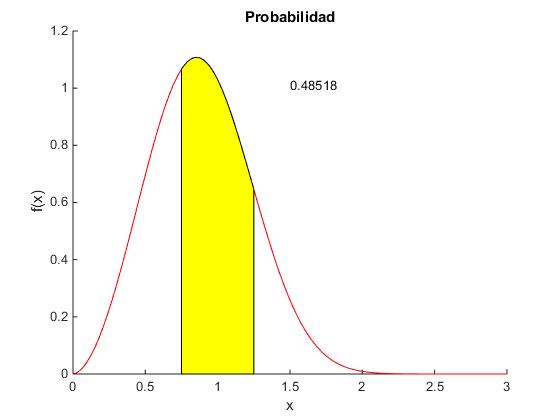
Obtenemos el mismo resultado efectuando la integración numérica de la función de Weibull f(x) mediante la función
Finalmente, la probabilidad acumulada F(x) vale
Las funciones f(x) y F(x) tienen las siguientes características:
- f(x) es una función continua que cambia rápidamente, alcanza un máximo y vuelve a cero.
- F(x) crece de forma continua tendiendo asintóticamente a uno
Representamos esta función con c=1 y variando el parámetro k, creando script similar al anterior, cambiando la definición de la función de f(x) a F(x).
c=1;
K=[1.2 1.6 2.0 2.4 2.8];
f=@(k,x) 1-exp(-(x/c).^k);
x=linspace(0,2.5,100);
hold on
for i=1:length(K)
plot(x,f(K(i),x),'displayName',num2str(K(i)))
end
ylim([0 1.2])
xlabel('x')
ylabel('f(x)')
title('Probabilidad acumulada')
legend('-DynamicLegend','location','SouthEast')
hold off
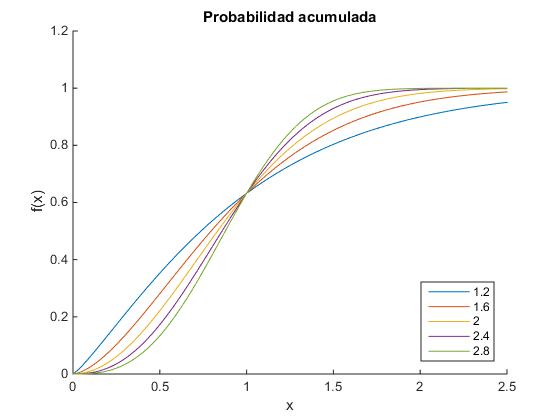
Ajuste de los datos a la función de Weibull
Mediante el script
| orden, i | velocidad, x | observaciones, w | frecuencia , f | frecuencia acumulada, F |
|---|---|---|---|---|
| 1 | 0.5 | 6 | 0.0081 | 0.0081 |
| 2 | 1.5 | 31 | 0.0417 | 0.0479 |
| 3 | 2.5 | 30 | 0.0403 | 0.0901 |
| 4 | 3.5 | 50 | 0.0672 | 0.1573 |
| 5 | 4.5 | 69 | 0.0927 | 0.2500 |
| 6 | 5.5 | 75 | 0.1008 | 0.3508 |
| 7 | 6.5 | 60 | 0.0806 | 0.4315 |
| 8 | 7.5 | 59 | 0.0793 | 0.5108 |
| 9 | 8.5 | 69 | 0.0927 | 0.6035 |
| 10 | 9.5 | 61 | 0.0820 | 0.6855 |
| 11 | 10.5 | 43 | 0.0578 | 0.7443 |
| 12 | 11.5 | 44 | 0.0591 | 0.8024 |
| 13 | 12.5 | 54 | 0.0726 | 0.8750 |
| 14 | 13.5 | 43 | 0.0578 | 0.9328 |
| 15 | 14.5 | 21 | 0.0282 | 0.9610 |
| 16 | 15.5 | 11 | 0.0148 | 0.9758 |
| 17 | 16.5 | 7 | 0.0094 | 0.9852 |
| 18 | 17.5 | 4 | 0.0054 | 0.9906 |
| 19 | 18.5 | 2 | 0.0027 | 0.9933 |
| 20 | 19.5 | 1 | 0.0013 | 0.9946 |
| 21 | 20.5 | 1 | 0.0013 | 0.9960 |
| 22 | 21.5 | 3 | 0.0040 | 1.0000 |
Para calcular la frecuencia acumulada se ha llamado a la función
>> horas/sum(horas) %frecuencia >> cumsum(horas)/sum(horas) %frecuencia acumulada
Ajuste no lineal
Para ajustar los datos de la columna frecuencia a la función de Weibull tendremos que determinar los valores de los parámetros c y k. Haremos un ajuste no lineal con la función
En color azul claro vemos el diagrama de frecuencias y en color rojo la función de Weibull que mejor ajusta.
clear,clc
velocidad=xlsread('WhiteDeer2013','Mar','F2:F745');
%interpolar si es necesario
if any(isnan(velocidad)) %si hay algún NaN
x=1:length(velocidad);
i=find(~isnan(velocidad));
velocidad=interp1(x(i),velocidad(i),x);
end
%histograma
x=0.5:1:max(velocidad);
horas=hist(velocidad,x);
%convierte a frecuencias y ajusta a la función de Weibull
frec=horas/sum(horas);
f=@(a,x) (a(1)/a(2))*((x/a(2)).^(a(1)-1)).*exp(-(x/a(2)).^a(1));
a0=[2 8]; %valor inicial de los parámetros
af=nlinfit(x,frec,f,a0)
hold on
%diagrama de frecuencias
bar(x,frec,'c');
%representa la curva de ajuste
x=linspace(0,max(velocidad),100);
y=f(af,x);
plot(x,y,'r')
title('Ajuste a la función Weibull')
xlabel('Velocidad')
ylabel('Frecuencia')
hold off
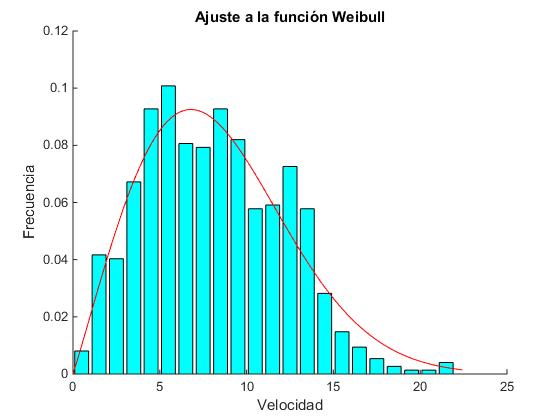
En la ventana de comandos obtenemos los valores de los parámetros k y c de ajuste
af = 2.0486 9.4165
El dato de k=
Ajuste lineal
En la expresión de las frecuencias acumuladas F(x), despejamos 1-F(x) y tomamos dos veces logaritmos neperianos.
Esta ecuación es la de una línea recta de pendiente a y de ordenda en el origen b.
z=au+b
donde u y z son variables
z=ln[-ln(1-F(x))]
a=k
u=lnx
b=-klnc
Hay que tener en cuenta que se produce un error cuando la frecuencia acumulada F(xn)=1, ya que MATLAB tiene que calcular el logaritmo neperiano de 0 que da
clear,clc
velocidad=xlsread('WhiteDeer2013','Mar','F2:F745');
%interpolar si es necesario
if any(isnan(velocidad)) %si hay algún NaN
x=1:length(velocidad);
i=find(~isnan(velocidad));
velocidad=interp1(x(i),velocidad(i),x);
end
%histograma
x=0.5:1:max(velocidad);
horas=hist(velocidad,x);
frec=horas/sum(horas); %frecuencias
%convierte a frecuencias acumuladas y ajusta a una línea recta
fcum=cumsum(frec);
z=log(-log(1-fcum));
z(length(z))=[];
u=log(x);
u(length(z))=[];
p=polyfit(u,z,1) %p(1) es la pendiente y p(2) es la ordenada en el origen
hold on
%representa la juste
plot(u,z,'ro','markersize',4,'markerfacecolor','r')
z=p(1)*u+p(2);
plot(u,z,'b')
title('Ajuste lineal')
xlabel('x')
ylabel('y')
hold off
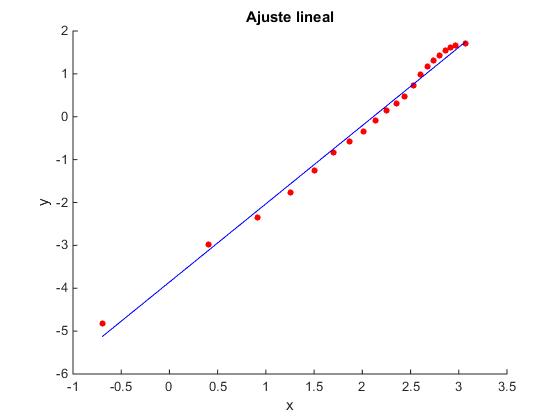
p = 1.8253 -3.8557
La pendiente de la recta de ajuste
k=
c=exp(-
k=1.8253 y c=8.2680
que difieren ligeramente de los calculados mediante el ajuste no lineal
Nos queda añadir al script la representación de las frecuencias y la función de Weibull con los parámetros calculados por el procedimiento de ajuste lineal para producir una figura similar a la del apartado anterior.
El código que añadimos al script para producir esta figura es el siguiente
%representación gráfica de frecuencias y función de Weibull
figure
k=p(1)
c=exp(-p(2)/k)
f=@(x) (k/c)*((x/c).^(k-1)).*exp(-(x/c).^k); %función de Weibull
hold on
%diagrama de barras
bar(x,frec,'c');
%representa la curva de juste
x=linspace(0,max(velocidad),100);
plot(x,f(x),'r')
title('Ajuste a la función Weibull')
xlabel('Velocidad')
ylabel('Frecuencia')
hold off
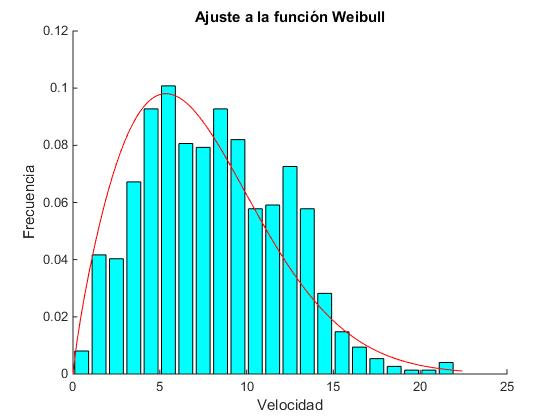
Se producen dos figuras: la recta de ajuste y la representación del diagrama de frecuencias junto a la función Weibull que mejor ajusta. Nos devuelve los valores de los parámetros k y c.
k = 1.8253 c = 8.2680
Comparación de las medidas y el modelo estadístico
En este sección vamos a comparar los resultados estadísticos obtenidos con las medidas de la velocidad del viento con los proporcionados por el modelo estadístico de Weibull que hemos ajustado a las frecuencias por dos procedimientos distintos: no lineal y lineal.
Valor medio y desviación estándar
Calculamos el valor medio de las 744 medidas de la velocidad del viento a lo largo del mes de marzo con las funciones
Utilizando el modelo estadístico de Weibull
El valor medio de la velocidad del viento se obtiene:
<x>=c·Γ(1+1/k)
La desvación estándar σ
En la sección anterior hemos obtenido los valores de los parámetros k y c:
- Ajuste no lineal, (k=2.0486, c=9.4165)
- Ajuste lineal, (k=1.8253, c=8.2680)
Creamos el script para comparar los resultados
clear,clc
velocidad=xlsread('WhiteDeer2013','Mar','F2:F745');
%interpolar si es necesario
if any(isnan(velocidad)) %si hay algún NaN
x=1:length(velocidad);
i=find(~isnan(velocidad));
velocidad=interp1(x(i),velocidad(i),x);
end
%media y desviación estándar de las medidas de la velocidad del viento
media=mean(velocidad)
estandar=std(velocidad)
%Modelo estadístico de Weibull
%ajuste no lineal
k=2.0486,c=9.4165
media=c*gamma(1+1/k)
estandar=c*sqrt(gamma(1+2/k)-gamma(1+1/k)^2)
%ajuste lineal
k=1.8253,c=8.2680
media=c*gamma(1+1/k)
estandar=c*sqrt(gamma(1+2/k)-gamma(1+1/k)^2)
media = 8.1741 estandar = 3.9761 k = 2.0486 c = 9.4165 media = 8.3421 estandar = 4.2674 k = 1.8253 c = 8.2680 media = 7.3479 estandar = 4.1711
Tiempo de funcionamiento de un aerogerador
Un aerogerador funciona cuando la velocidad del viento es superior a un valor mínimo (cut-in) e inferior a un valor máximo (cut-out). Para un hipotético aerogenerador estas velocidades son 4 m/s y 18 m/s, respectivamente. Calcular el número de horas a lo largo del mes de marzo que el aerogenerador ha estado generando energía eléctrica.
A partir de las medidas de la velocidad del viento guardadas en el vector
En el modelo estadístico de Weibull, la probabilidad de que la velocidad del viento x esté en el intervalo comprendido entre x0 y x1 se calcula mediante la siguiente expresión
Hacemos estos cálculos con MATLAB
clear,clc
velocidad=xlsread('WhiteDeer2013','Mar','F2:F745');
%interpolar si es necesario
if any(isnan(velocidad)) %si hay algún NaN
x=1:length(velocidad);
i=find(~isnan(velocidad));
velocidad=interp1(x(i),velocidad(i),x);
end
%horas a partir de las medidas de la velocidad del viento
x0=4;x1=18;
horas=sum(velocidad>=x0 & velocidad<=x1)
%Modelo estadístico de Weibull
%ajuste no lineal
k=2.0486,c=9.4165
prob=exp(-(x0/c)^k)-exp(-(x1/c)^k);
horas=length(velocidad)*prob
%ajuste lineal
k=1.8253,c=8.2680
prob=exp(-(x0/c)^k)-exp(-(x1/c)^k);
horas=length(velocidad)*prob
>> weibull_6 horas = 622 k = 2.0486 c = 9.4165 horas = 608.6147 k = 1.8253 c = 8.2680 horas = 558.5172
El ajuste no lineal parece que proporciona unos resultados más cercanos a los que se obtienen directamente a partir de las medidas de las velocidades del viento.

