Medidas de la velocidad y dirección del viento

Con fecha 22-05-2013 se ha descargado el fichero WhiteDeer2013.xls desde la web de Alternative Energy Institute, en la dirección http://www.windenergy.org/datasites/14-whitedeer/, se trata de un fichero Excel que contiene varias hojas. Alternativamente, se puede descargar desde este enlace WhiteDeer2013.xls

La información del sitio denominado WhiteDeer 0614 (N 35° W 101°) nos proporciona los datos de las velocidades del viento de 6 estaciones denominadas WS1 a WS6 y las direcciones del viento de tres estaciones denominadas WD1 a WD3. Los datos más completos los podemos encontrar en las hojas Mar (Marzo) y Apr (Abril) de este año 2013.

WS1 y WS2 se encuentran a 50 m, WS3 y WS4 a 40 m, y WS5 y WS6 a 10 m de altura, respectivamente. WD1 se encuentra a 50 m, WD2 a 40 m y WD3 a 25 metros de altura, respectivamente.

Los datos han sido tomados en intervalos de tiempo de una hora de duración, y junto al dato de la velocidad media o dirección media (ave) en ese intervalo de tiempo, se proporciona en la columna adyacente (std) la desviación estándar.

Situamos el fichero WhiteDeer2013.xls en la carpeta de ficheros accesible a MATLAB.

Direcciones de la velocidad del viento

En primer lugar, vamos a examinar los datos de las direcciones de la velocidad del viento del mes de marzo, para lo cual cargaremos en MATLAB los datos contenidos en la hoja Mar columna R (estación WD1) desde la fila 2 a la fila 745, que corresponden a las direcciones medias del viento tomadas en el mes de marzo asignados a las horas 0 a 23 desde los días 1-03-2013 hasta el 31-03-2013.

Cargamos mediante la función xslread los datos de hoja Mar y la columna R desde la fila 2 a la fila 745 y lo asignamos al vector angulo.

>> angulo=xlsread('WhiteDeer2013','Mar','R2:R745');
>> length(angulo)
ans =
   744

Comprobamos en la ventana Workspace y mediante length que el vector angulo contiene 744 elementos. Este es el producto de 31 días del mes de marzo × 24 horas = 744 datos.

Ahora, examinamos si hay alguna celda que no contiene datos y que al cargarse en MATLAB se ha transformado en NaN.

>> c=find(isnan(angulo))
c =
   464
>> angulo(c)=[];
>> length(angulo)
ans =
   743

Vamos a la hoja de cálculo Mar y observamos que la celda situada en la fila 465 y en la columna R está vacía, no contiene ningún dato. Nuestra opción ahora es eliminar este dato o interpolarlo. Eliminarlo es un proceso sencillo como se mestra en el cuadro más arriba, interpolarlo es algo más complicado, pero conserva el número total de datos y la secuenciación en el tiempo. Elegimos la segunda opción.

>> angulo=xlsread('WhiteDeer2013','Mar','R2:R745');
>> c=find(isnan(angulo))
c =
   464
>> angulo(464)
ans =
   NaN
>> x=1:length(angulo);
>> i=find(~isnan(angulo));
>> y=interp1(x(i),angulo(i),x);
>> angulo=y; 
>> angulo(464)
ans =
    44

Después de interpolar linealmente el elemento 464 del vector angulo que contenía un NaN ahora guarda un ángulo de 44 grados. Fijarse que 44 es el valor medio entre el ángulo inmediatamente anterior angulo(463)=38 y el ángulo inmediatamente posterior angulo(465)=50.

Encontramos las horas que la veleta apunta en un determinado intervalo angular del siguiente modo.

>> sum(angulo>0 & angulo<=10)
ans =
    22
>> sum(angulo>10 & angulo<=20)
ans =
    19
>> sum(angulo>20 & angulo<=30)
ans =
    37

La veleta ha estado orientada 22 horas en una dirección comprendida entre 0 y 10 grados.
La veleta ha estado orientada 19 horas en una dirección cmprendida entre 10 y 20 grados.
La veleta ha estado orientada 37 horas en una dirección comprendida entre 20 y 30 grados

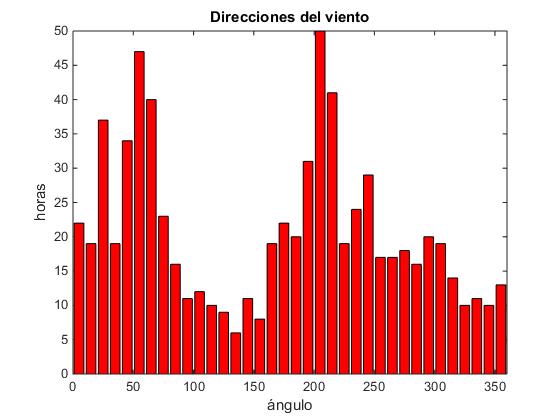
Agupamos los 744 datos de ángulos en intervalos de 10 grados mediante la función hist de MATLAB, la cual admite un vector x como segundo argumento que le indica a hist como agrupar los datos guardados en el vector angulo. Así hist agrupará los datos en intervalos de anchura 10 grados centrados en los ángulos 5, 15, 25, 35... grados.

>> x=5:10:355;
>> horas=hist(angulo,x);
>> bar(x,horas);

La función hist devuelve el vector horas que contiene el número de ángulos que caben en cada intervalo definido por el vector x. La función bar representa gráficamente el histograma. En el eje horizontal los ángulos divididos en intervalos de 10 grados. En el eje vertical el número de ángulos del vector angulo que caben en cada intervalo. El número de ángulos es igual al número de horas en el mes de marzo que la veleta apunta en una determinada dirección angular.

El valor máximo guardado en el vector horas lo obtenemos mediante la función max y luego, mediante la función find obtenemos el índice del elemento que guarda el valor máximo

>> find(horas==max(horas))
ans =
    21 %indice
>> x(21)
ans =
   205
>> horas(21)
ans =
    50 %valor máximo

La dirección predominante del viento es 205 grados. En la dirección comprendida entre 200 y 210 grados la veleta ha estado orientada 50 horas.

clc,clear
angulo=xlsread('WhiteDeer2013','Mar','R2:R745');

%interpolar
if any(isnan(angulo)) %si hay algún NaN
    x=1:length(angulo);
    i=find(~isnan(angulo));
    angulo=interp1(x(i),angulo(i),x);
end

%agrupar los datos en intervalos. Histograma
x=5:10:355;
horas=hist(angulo,x);

%diagrama polar
x1=[x 365];
ang=x1*pi/180;
horas1=[horas horas(1)];
gc=polar(ang,horas1,'r');
set(gc, 'linewidth',2);
title('Direcciones del viento')

%diagrama de barras
figure
bar(x,horas,'r');
xlim([0 360])
title('Direcciones del viento')
xlabel('ángulo')
ylabel('horas')

En un diagrama polar apreciamos mejor las direcciones predominantes del viento medidos por la estación WD1.

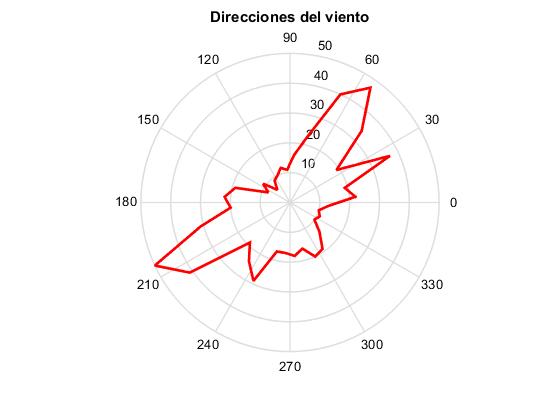
Velocidades del viento

Analizaremos ahora las velocidades del viento medidas por la estación WS1 que se encuentran en la columna F desde la fila 2 hasta la fila 745, en total tenemos 744 datos=24 horas × 31 días del mes de marzo.

Cargamos los datos en MATLAB para crear el vector velocidad de 744 elementos.

>> velocidad=xlsread('WhiteDeer2013','Mar','F2:F745');
>> length(velocidad)
ans =
   744
>> c=find(isnan(velocidad))
c =
   Empty matrix: 0-by-1

Todas las celdas de la columna F contienen datos, no hay ninguna vacía. El vector velocidad no contiene ningún elemento cuyo valor sea NaN.

Mostramos el valor máximo y mínimo que contiene el vector velocidad mediante las funciones max y min, respectivamente.

>> c=find(velocidad==max(velocidad))
c =
   220
>> velocidad(c)
ans =
   22.4000
>> c=find(velocidad==min(velocidad))
c =
   116
>> velocidad(c)
ans =
    0.7000

El índice del vector velocidad se puede convertir fácilmente en tiempo (día y hora del mes de marzo) dividiendo entre 24:

El elemento 220 del vector velocidad contiene el dato guardado en la celda de la fila 221 y de la columna F correspondiente al día 10 a las 3 h. La máxima velocidad se detectó a esta hora.
El elemento 116 del vector velocidad contiene el dato guardado en la celda de la fila 117 y de la columna F correspondiente al día 5 a las 19 h. La mínima velocidad se detectó a esta hora.

Generamos el vector tiempo en vez de leerlo en las columnas B (Date) y C (Time) de la hoja Mar, y representamos gráficamente en el eje horizontal el tiempo de 1 a 744 y en el eje vertical la velocidad, para mostrar la gran variabilidad de la velocidad del viento

>> t=1:length(velocidad);
>> plot(t,velocidad)
>> xlim([0 745])
>> xlabel('mes de marzo')
>> ylabel('velocidad')

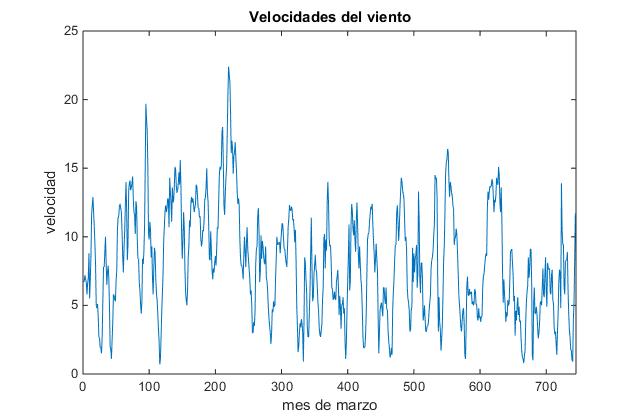
Vamos a ver con más detalle la velocidad del viento día a día. En la gráfica se representa la velocidad del viento el 3 de Marzo. Introducimos el día del mes y se representa la velocidad del media del viento tomadas en intervalos de una hora de duración, le asignamos estos valores a la hora 0.5, 1.5, 2.5... 23.5

clear,clc
dia=input('Día del mes (1-31): ');
velocidad=xlsread('WhiteDeer2013','Mar','F2:F745');
%interpolar
if any(isnan(velocidad)) %si hay algún NaN
    x=1:length(velocidad);
    i=find(~isnan(velocidad));
    velocidad=interp1(x(i),velocidad(i),x);
end

indice=1:length(velocidad);
x=0.5:1:23.5;
vel_mes=velocidad(indice>(dia-1)*24 & indice<=dia*24);
hold on
plot(x,vel_mes,'ro','markersize',2,'markerfacecolor','r');
plot(x,vel_mes,'b')
xlim([0 24])
title('Velocidad del viento en un día')
xlabel('velocidad')
ylabel('hora')
hold off

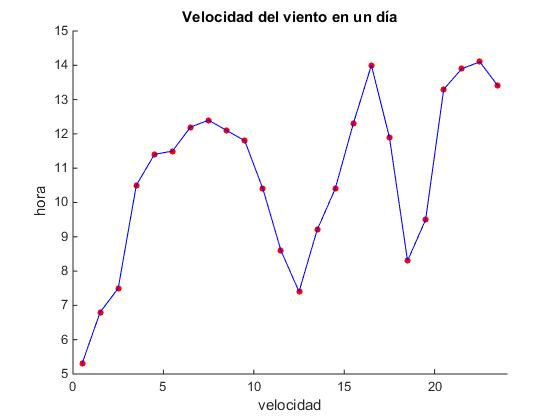
En la ventana de comandos corremos el script

>> viento_2
Día del mes (1-31): 3

Dada la gran variabilidad del viento no obtendremos información relevante si no hacemos un análisis estadístico. Comenzamos agrupando las medidas de la velocidad del viento.

Vamos a determinar el número de medidas (horas) en las que la velocidad del viento tiene un valor medio comprendido entre 0 y 1 m/s, entre 1 y 2, ... entre 22 y 23 que alcanza la máxima velocidad mediante la función hist de MATLAB

>> x=.5:1:23;
>> horas=hist(velocidad,x);
>> bar(x,horas,'r')
>> title('velocidades del viento')
>> xlabel('velocidad')
>> ylabel('horas')

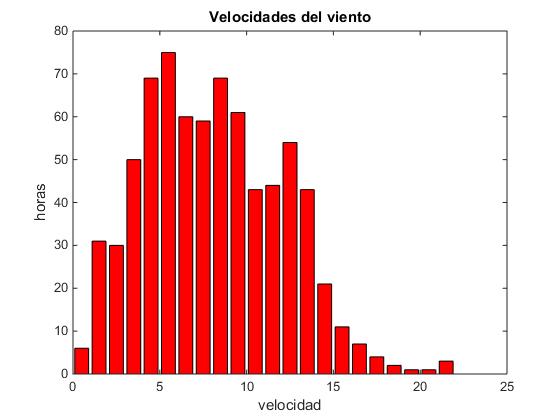
Con los fragmentos de código de esta sección elaboramos un script para dibujar este histograma.

clear,clc
velocidad=xlsread('WhiteDeer2013','Mar','F2:F745');

%interpolar
if any(isnan(velocidad)) %si hay algún NaN
    x=1:length(velocidad);
    i=find(~isnan(velocidad));
    velocidad=interp1(x(i),velocidad(i),x);
end

%histograma
x=0.5:1:max(velocidad);
horas=hist(velocidad,x);
bar(x,horas,'r');
title('Velocidades del viento')
xlabel('velocidad')
ylabel('horas')