Transformada rápida de Fourier (II)
Posición del asteriode Pallas
Gauss estaba interesado en calcular de un modo preciso la órbita del asteroide Pallas, a partir de las observaciones de su posición.
| Ascensión | 0 | 30 | 60 | 90 | 120 | 150 | 180 | 210 | 240 | 270 | 300 | 330 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Declinación | 408 | 89 | -66 | 10 | 338 | 807 | 1238 | 1511 | 1583 | 1462 | 1183 | 804 |
Disponía de 12 pares de datos (xi,yi) que deseaba interpolar con seis funciones armónicas.
y= A0+A1cos(ωx)+ B1sin(ωx)+ A2cos(2ωx)+ B2sin(2ωx)+...+ A6cos(6ωx)+ B6sin(6ωx)
Al final de la página Ajuste de datos con funciones armónicas hemos tratado este mismo problema. Ahora, vamos a calcular los coeficientes A0...A6 y B1...B6 a partir de la Transformada Rápida de Fourier
x=0:30:330;
y=[408 89 -66 10 338 807 1238 1511 1583 1462 1183 804];
hold on
plot(x,y,'ro','markersize',3,'markerfacecolor','r')
n=length(y);
w=2*pi/360;
d=fft(y);
M=floor((n+1)/2);
a0=d(1)/n;
a=2*real(d(2:M))/n;
a(6)=d(M+1)/n;
b=-2*imag(d(2:M))/n;
b(6)=0;
x=0:360;
k=1:6;
y=a0+a*cos(w*k'*x)+b*sin(w*k'*x);
plot(x,y,'b')
hold off
xlim([0 360])
xlabel('Ascensión (grados)')
ylabel('Declinación (minutos)')
title('Posición del asteroide Pallas')
grid on
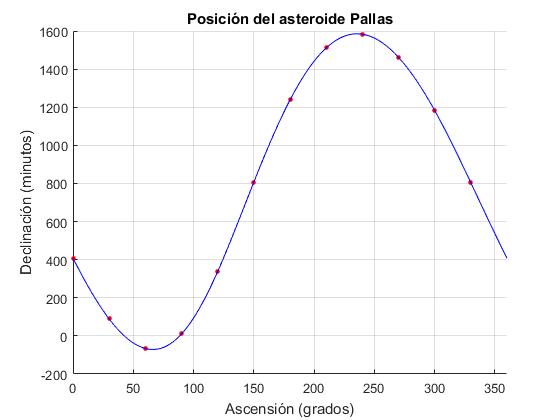
La solución encontrada por Gauss es equivalente a la Transformada Rápida de Fourier que fué descubierta mucho más tarde en 1965 por John Turkey y John Cooley
Manchas solares

(USET data/image, Royal Observatory of Belgium, Brussels, http://sidc.oma.be/uset/)
Durante siglos los astrónomos han notado que la superficie del Sol no es constante o uniforme en apariencia y que ciertas regiones oscuras aparecen en posiciones aleatorias con una base cíclica. En 1848, Rudolf Wolfer propuso una regla que combinaba el número y el tamaño de estas manchas solares en un único índice. Usando archivos históricos, los astrónomos aplicaron la regla de Wolfer para determinar la actividad de las manchas solares desde el año 1700.
De esta web y desde la dirección http://sidc.oma.be/sunspot-data/ se pueden descargar los datos de las manchas solares en un fichero ASCII. Desde el enlace yearly sunspot number se ha descargado el fichero
| Año | Indice Wolfer |
|---|---|
1700.5 1701.5 1702.5 1703.5 1704.5 1705.5 1706.5 1707.5 ....... 2007.5 2008.5 2009.5 2010.5 2011.5 2012.5 |
5.0 11.0 16.0 23.0 36.0 58.0 29.0 20.0 ...... 7.5 2.9 3.1 16.5 55.7 57 |
Situamos este fichero en la carpeta por defecto (Current folder). Creamos un script para cargar con el comando
load yearssn.dat
t=yearssn(:,1); %año
m_s=yearssn(:,2); %número de manchas solares
hold on
plot(t,m_s,t,m_s,'bo','markersize',3,'markerfacecolor','b')
p=polyfit(t,m_s,1);
trend=polyval(p,t);
plot(t,trend)
hold off
xlim([1700 2020])
xlabel('Año')
ylabel('Número manchas solares')
grid on
title('Actividad solar')
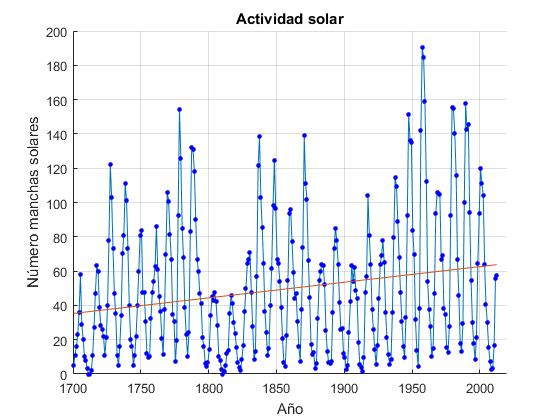
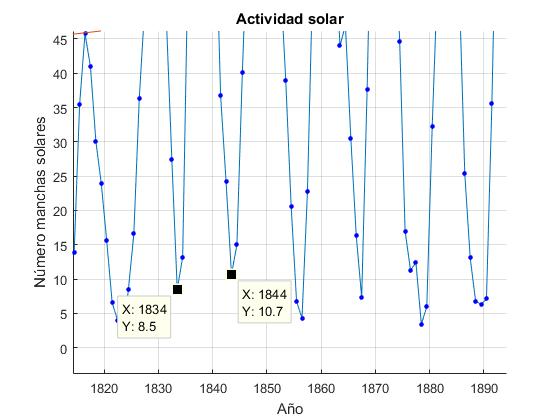
Se puede observarse fácilmente la tendencia cíclica del fenómeno: los picos y los valles se encuentran separados entre sí algo más de 10 años (podemos seleccionar una parte de la imagen y ampliarla eligiendo los iconos Zoom y Pan debajo del menú de Figure Window). Con Data cursor señalamos dos picos consecutivos y medimos su diferencia en años (10)
La línea de color roja indica la tendencia media de los datos obtenida mediante ajuste por mínimos cuadrados llamando a la función MATLAB
Tomamos como intervalo de tiempo Δt=1 año. Creamos la serie de frecuencias angulares del mismo modo que en el ejemplo anterior, siendo n es el número de datos y la frecuencia crítica o de Nyquist ωc=π/Δt=π rad/año.
Escribimos un script que primero crea la serie temporal (t,f) a partir de los datos originales y después la serie (ω,g) mediante la Transformada Rápida de Fourier
load yearssn.dat
t=yearssn(:,1); %año
m_s=yearssn(:,2); %número de manchas solares
f=detrend(m_s);
plot(t,f)
xlim([1700 2020])
xlabel('Año')
ylabel('Número manchas solares')
title('Serie temporal')
n=length(f);
dt=1; %año
dw=2*pi/(n*dt);
w=(0:n-1)*dw;
wc=pi/dt; %frecuencia angular crítica
g=fft(f);
power=abs(g).^2;
figure
stem(w,power,'markersize',4,'markerfacecolor','r')
xlim([0 wc])
[M,I]=max(power);
periodo=2*pi/w(I);
text(w(I)+.1,power(I), ['periodo',num2str(periodo)]);
grid on
xlabel('rad/año')
ylabel('Potencia')
title('Espectro de frecuencias')
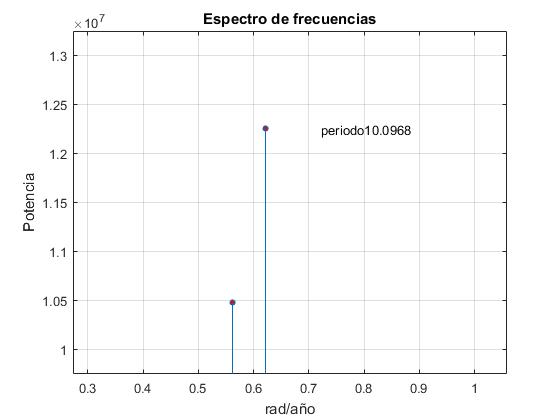
calculamos el periodo de forma más exacta, utilizando la función
Concentración de CO2 en la atmósfera.
La curva de Keeling es una gráfica de la concentración de dióxido de carbono en la atmósfera desde 1958. Las medidas fueron tomadas en Mauna Loa (Hawái) bajo la supervisión de Charles David Keeling. Muestran los rápidos incrementos en los niveles de dióxido de carbono en la atmósfera
Los datos se encuentran en el fichero
Se guarda este fichero en carpeta de trabajo de MATLAB, se crea un script mediante New Script. En la pestaña Home se pulsa en Import data y se carga el fichero
En Output type seleccionamos Column vectors, indicando que no nos interesa toda la tabla de datos (diez columnas), solamente estamos interesados en la columna E que guarda las concentraciones de CO2 en ppm. Al principio de la columna y al final, hay celdas que contienen el dato -99.99, quiere decir que en ese mes no se ha medido la concentración de CO2. A partir de 1965/01 (enero) y hasta 2020/07 (julio), todas las celdas guardan medidas.
Seleccionamos mediante el ratón o en Range, en la columna E desde E142 hasta E808 ambos inclusive y pulsamos el botón Import selection. En la ventana Workspace cambiamos el nombre de la variable a
Representamos gráficamente estos datos, mediante un script. Dentro de la ventana gráfica representamos las medidas de la concentración en cada uno de los meses del año 1965.
plot(co)
grid on
xlim([1,667])
set(gca,'XTick',1:60:667)
set(gca,'XTickLabel',1965:5:2020)
xlabel('Año')
ylabel('Concentración CO_2, ppm')
title('Concentración CO_2, promedio mensual')
axes('Position',[0.21,0.58,2/7,3/10])
hold on
plot(co(1:12));
plot(co(1:12),'ro','markersize',3,'markerfacecolor','r');
hold off
grid on
title('variación mensual')
box off
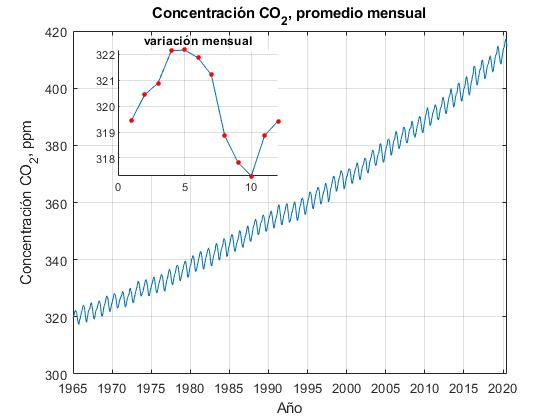
La causa de las oscilaciones de la concentración se deben a la absorción y a la liberación del CO2 por la vegetación. En el hemisferio norte, en la primavera y verano crecen las plantas que absorben el CO2 de la atmósfera en el proceso de la fotosíntesis. Por otra parte, en el otoño y en el invierno las plantas pierden sus hojas y el el CO2 se libera a la atmósfera. El periodo de oscilación de la concentración de CO2 coincidirá con el tiempo que tarda la Tierra en dar una vuelta alrededor del Sol
Creamos otro script. Importamos el fichero de datos mencionado. En este caso, seleccionamos 28=256 datos de la columna E. Desde E538 hasta E793, desde enero (01) de 1998 hasta abril (04) de 2019. Guardamos los datos en el vector
El primer paso, es utilizar el comando
t=1:256;
hold on
Fs=1; %frecuencia de muestreo. Inversa del intervalo de tiempo, un mes
f=(0:(length(co_1)-1)/2)*(Fs/length(co_1));
D=detrend(co_1);
FD=fft(D);
Amp=abs(FD(1:length(FD)/2));
plot(f,Amp);
[M,I]=max(Amp); %máximo
plot(f(I),M,'ro','markersize',4,'markerfacecolor','r')
text(f(I)+0.01,M, ['periodo: ',num2str(1/f(I))]);
hold off
grid on
xlabel('frecuencia, 1/mes')
ylabel('Amplitud')
title('Espectro de frecuencias')
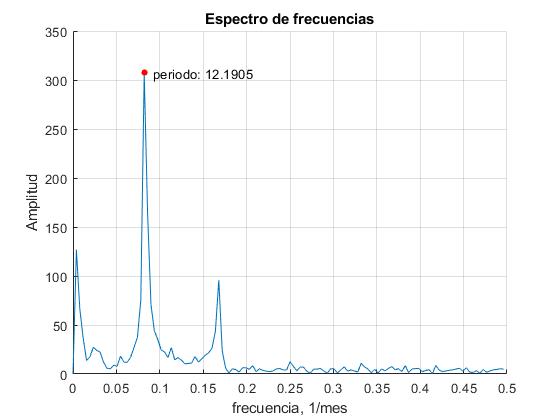
Obtenemos un periodo algo mayor de 12 meses.
Ejemplos en el curso de Física
Análisis armónico de las mareas
Análisis de Fourier de los desplazamiento de las olas
Resumen
| dt | intervalo de tiempo | dw=2π/(n·dt) | intervalo de frecuencias angulares |
|---|---|---|---|
| vector de tiempos | vector de frecuencias angulares | ||
| (tj,xj) | serie temporal | Transformada Rápida de Fourier. Los elementos del vector g son números complejos | |
| número de datos | potencia | ||
| fs=1/dt | frecuencia de muestreo | ωc=π/dt | frecuencia angular crítica (Nyquist) |
Referencias
Del apartado titulado, 'Concentración de CO2 en la atmósfera'.
Unofre B Pili, Renante R Violanda. Extracting Earth's orbital period from atmospheric CO2 concentrations using the Fourier transform based on Matlab. Phys. Educ. 55 (2020) 055001

