Preparando los datos

No es un número (NaN)

NaN significa, no es un número y representa el resultado de operaciones matemáticas indefinidas tales como 0/0 o ∞-∞ (infinito menos infinito). isnan(x) es una función que devuelve uno si x es NaN y cero en caso contrario.

NaN se utiliza para marcar datos que no se han podido proporcionar por alguna causa (fallo en el dispositivo medidor, en la comunicación o archivo de los datos) como en el siguiente vector, u=[-2,10,5,NaN,-3,8,2,NaN,6];

>> u=[-2,10,5,NaN,-3,8,2,NaN,6];
>> isnan(u)
ans =     0     0     0     1     0     0     0     1     0
>> find(isnan(u))
ans =     4     8

Si queremos analizar los datos guardados en el vector u que contiene NaN, tenemos problemas. Por ejemplo, queremos calcular la media, mean, de los datos guardados en el vector u.

>> mean(u)
ans =   NaN

Tenemos varias formas de eliminar los elementos que son NaN tal como vemos en el siguiente cuadro. Una vez eliminados podemos calcular la media mean de los elementos de un vector que no son NaN.

>> u=[-2,10,5,NaN,-3,8,2,NaN,6];
>> v=u(find(~isnan(u)))
v =    -2    10     5    -3     8     2     6
>> v=u(~isnan(u))
v =    -2    10     5    -3     8     2     6
>> u(isnan(u))=[]
u =    -2    10     5    -3     8     2     6
>> mean(u)
ans =    3.7143

Creamos una pequeña rutina que detecte si hay NaN en el vector u y en ese caso, los elimine.

u=[-2,10,5,NaN,-3,8,2,NaN,6];
if any(isnan(u))
    v=u(~isnan(u))
end

o alternativamente,

u=[-2,10,5,NaN,-3,8,2,NaN,6];
if any(isnan(u))
    indices=find(isnan(u));
    u(indices)=[]
end

La función nanmean calula la media de los elementos del vector u ignorando los NaN. Hay varias funciones más que empiezan por nan y los ignoran: nanmax, nanmin, nanstd, nansum, etc.

>> nanmean(u)
ans =    3.7143

Cargando ficheros de datos

Supongamos que tenemos un conjunto de datos guardados en el fichero de texto datos.txt, tal como se muestra en la figura.

La primera columna, es el número de orden, pero podría ser tiempo o cualquier otra variable. La segunda columna es la secuencia de la medida de una variable: velocidad del viento a una determinada altura, temperatura en una localidad en distintos días a la misma hora, etc.

Como vemos las dos columnas están separadas por espacios, pero podría utilizarse otros delimitadores como comas, tabuladores, etc.

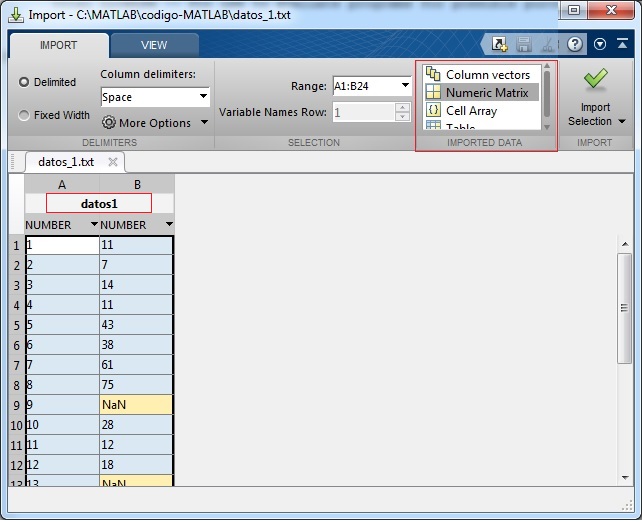
El primer paso, es importar el fichero datos.txt en MATLAB mediante el asistente de la importación de datos, Import data..., pera ello hemos de situar el fichero de datos en la carpeta de trabajo de MATLAB (Current Folder).

Seleccionamos el fichero datos.txt

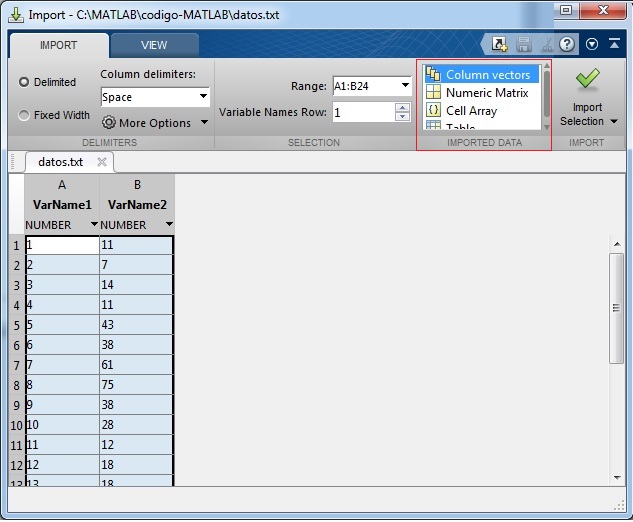
Vemos las dos columnas de datos dispuestos en filas y columnas de forma similar a como aparecen en una hoja de cálculo.Pulsamos el botón titulado Import Selection (Import Data)

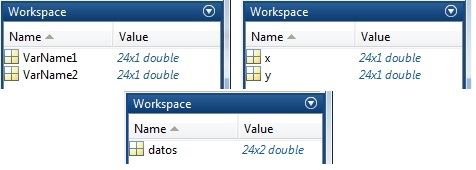
Se generan dos vectores VarName1 y VarName2 que contienen los datos de la primera columna y de la segunda, respectivamente. Pulsando el botón derecho del ratón sobre cada uno de los nombres de las variables, elegimos en el menú flotante, Rename para cambiar los nombres de dichas variables por x e y.

Si en el control de selección situado en la pestaña IMPORT, titulado IMPORTED DATA elegimos Numeric Matrix en vez del valor por defecto Column vectors se generará una matriz datos con el mismo nombre que el fichero de texto que ha sido importado.

Representando gráficamente los datos

El primer paso, es hacer una representación gráfica de los datos. Seleccionamos con el puntero del ratón las dos variables x e y, y en el menú flotante que aprece al pulsar el botón derecho del ratón elegimos plot(x,y). Alternativamente, en la ventana de comandos escribimos

>> plot(x,y))

Estadística de los datos

En el menú de la ventana Figure Window seleccionamos Tools/Data Statistics y aparece una nueva ventana

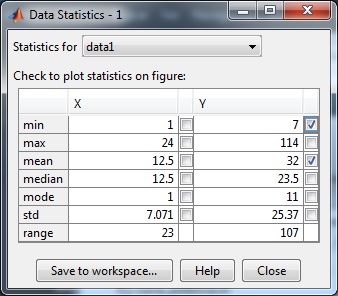
Nos porporciona el valor mínimo min, máximo, max, el valor medio, mean, la desviación estándar, std, de cada una de las columnas: X es la primera columna, Y es la segunda columna de data 1.

Si activamos la casilla mean correspondiente a la columna Y de data 1, se representa el valor medio 32 mediante una línea recta horizontal en el gráfico (Check to plot statistics on figure). Si activamos la casilla min aparece la recta horizontal que señala el mínimo, 7 de Y, y así, con el resto de las medidas estadísticas. El aspecto de la ventana gráfica es la siguiente

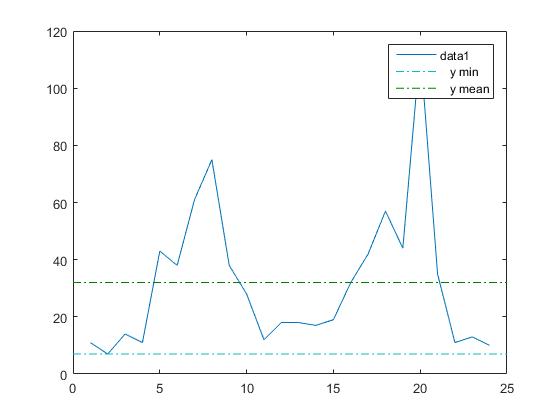
Una representación similar se obtiene si guardamos los datos en la matriz datos y en la ventana de comandos escribimos

>> plot(datos(:,1),datos(:,2))

Datos que se han perdido

A veces, en una serie grande de datos, algunos se pierden. Se tendrá que decidir si los datos perdidos se eliminan del análisis de datos o se reemplazan utilizando algún método tal como la interpolación.

En MATLAB, los datos no disponibles se representan por un valor especial denimoniado NaN (Not-a-Number)

El fichero datos1.txt es el mismo que datos.txt salvo que se han sustituido dos números de la segunda columna por NaN. Importamos los datos mediante el asistente Import data.... En el control de selección IMPORTED DATA elegimos Numeric Matrix. Al pulsar el botón Import Selection (Import Data), observamos en la ventana Workspace la matriz datos1 de dimensión 24×2

Para buscar los indices i,j de los elementos de la matriz datos1 que son NaN escribimos:

>> [i,j]=find(isnan(datos1))
i =
     9
    13
j =
     2
     2

Eliminando filas de la matriz de datos

Para eliminar las filas 9 y 13 de la matriz datos1 donde hay elementos NaN escribimos

>> datos1(i,:)=[]
datos1 =
     1    11
     2     7
     3    14
     4    11
     5    43
     6    38
     7    61
     8    75
    10    28
    11    12
    12    18
    14    17
    15    19
    16    32
    17    42
    18    57
    19    44
    20   114
    21    35
    22    11
    23    13
    24    10

Interpolando datos

Como hemos visto, los valores x=9 y x=13 no tiene correspondiente valor y. En el apartado anterior, decidimos eliminarlos de la matriz datos1. En esta ocasión vamos a asignarles a cada uno de ellos un valor en términos de los más próximos a x=9 y x=13.

Por defecto, el método de interpolación es el lineal, aunque hay otros procedimientos más sofisticados.

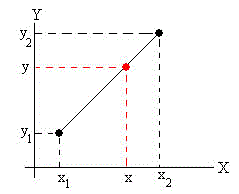
Conocemos los datos de (x₁, y₁) y de (x₂, y₂) y queremos conocer el valor desconocido de y cuando se porporciona la abscisa x₁<x<x₂. Si suponemos que los puntos 1 y 2 están unidos por una recta, calculamos fácilmente el valor de y mediante la siguiente relación

$y = y_{1} + \frac{y_{2} - y_{1}}{x_{2} - x_{1}} (x - x_{1})$

Como al valor x₁=8 le corresponde y₁=75, y a x₂=10 le corresponde y₂=28, al valor x=9 le corresponde y=51.5 de acuerdo con el procedimiento de interpolación lineal esquematizado en la figura. Del mismo modo, a x₁=12 le corresponde y₁=18 y a x₂=14 le corresponde y₂=17, al valor x=13 le corresponde y=17.5.

Vamos a ver como utilizamos los comandos MATLAB, para que se sustituyan los NaN de x=9 y x=13 de la matriz datos1 por los valores interpolados.

Cargamos de nuevo el fichero datos1.txt con el comando load de MATLAB en vez del asistente de importación de datos, para tardar menos tiempo.
Buscamos el índice de las filas que no contienen NaN mediante ~isnan. NOT isnan devuelve uno si no contiene NaN y cero si lo contiene.
Asignamos un valor y a x=9 y otro x=13 mediante el procedimiento de interpolación lineal llamando a la función MATLAB interp1. Esta función admite en su dos primeros argumentos el vector x y el vector y sin los NaN, y en el tercer argumento el vector x original, devuelve el vector y con los valores que faltan interpolados. Finalmente, reconstruimos la matriz datos1.

>> clear,clc % borrado de memoria (Workspace) y de ventana (Command Window)
>> load datos1.txt
>> i=find(~isnan(datos1(:,2)));
>> y=interp1(datos1(i,1),datos1(i,2),datos1(:,1));
>> datos1(:,2)=y  % reconstruimos la matriz datos1
datos1 =
    1.0000   11.0000
    2.0000    7.0000
    3.0000   14.0000
    4.0000   11.0000
    5.0000   43.0000
    6.0000   38.0000
    7.0000   61.0000
    8.0000   75.0000
    9.0000   51.5000
   10.0000   28.0000
   11.0000   12.0000
   12.0000   18.0000
   13.0000   17.5000
   14.0000   17.0000
   15.0000   19.0000
   16.0000   32.0000
   17.0000   42.0000
   18.0000   57.0000
   19.0000   44.0000
   20.0000  114.0000
   21.0000   35.0000
   22.0000   11.0000
   23.0000   13.0000
   24.0000   10.0000

Comprobar que se obtiene los mismo poniendo

>> i=find(~isnan(datos1(:,2)))
>> y=interp1(datos1(i,1),datos1(i,2),datos1(:,1))

que

>> i=~isnan(datos1(:,2))
>> y=interp1(datos1(i,1),datos1(i,2),datos1(:,1))

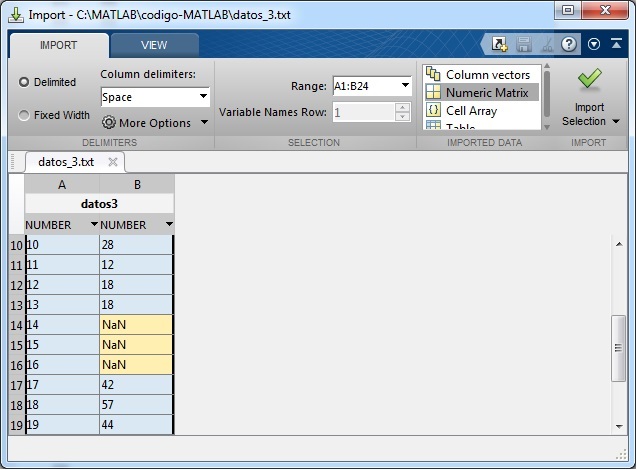
Finalmente, vamos a probar como se reconstruye el fichero de datos cuando faltan tres datos consecutivos. Creamos el fichero datos3.txt que le faltan los datos de índices 14,15 y 16 tal como se muestra en la figura.

>> clear,clc 
>> load datos3.txt
>> i=find(~isnan(datos3(:,2)))
>> y=interp1(datos3(i,1),datos3(i,2),datos3(:,1))
>> datos3(:,2)=y  
>> datos3 =
     1    11
     2     7
     3    14
     4    11
     5    43
     6    38
     7    61
     8    75
     9    38
    10    28
    11    12
    12    18
    13    18
    14    24
    15    30
    16    36
    17    42
    18    57
    19    44
    20   114
    21    35
    22    11
    23    13
    24    10