Datos de las olas del mar
A medida que sopla el viento, las fuerzas de fricción entre el aire y el agua origina elevaciones de la superficie del agua, que se van incrementando de altura, pudiendo alcanzar varios metros en las situaciones de temporal.
Los factores que determinan las olas generadas por el viento son los siguientes:
- La velocidad del viento
- La duración o el tiempo durante el cual el viento actúa
- La distancia a lo largo de la cual el viento sopla en la misma dirección
Las olas del mar no crecen indefinidamente, a partir de cierto momento la energía que el viento transmite al agua se disipa durante la rotura de la ola. La ola está plenamente desarrollada y no crece más.
Hay dos clases de olas por ejemplo, las que genera el viento en una tormenta que parecen caóticas y aquellas alejadas del foco productor que tienen un aspecto completamente diferente, formadas por largos picos y valles bien definidos que se propagan por la superficie del océano en calma.
En general, en la superficie del océano se propagan olas de altura y periodos variables que se mueven en diferentes direcciones. Esta es la razón por la que se estudia el estado de la superficie del mar de forma estadística.
Cuando medimos el estado de la superficie del océano desde una posición fija, las medidas aparecerán ciertamente irregulares. Observaremos una gran variabilidad en las alturas y periodos de las olas que van llegando.
Datos de las olas del océano
Hemos tomado de la web CDIP "The Coastal Data Information Program" los datos para la realización del análisis con MATLAB
En esta web se explica detalladamente, el proceso de adquisión y tratamiento de los datos tomados desde boyas.
Seleccionamos la pesataña Historic y en el margen izquierdo pinchamos en Subdirectories/Buoys para elegir una estación, por ejemplo, la número 067 situada en San Nicolas Island, California. En la página web que aparece, titulada San Nicolas Island, CA Conditions + Forecast seleccionamos en el margen izquierdo Single Run/Time series (xyz)
Vemos tres gráficas que corresponden a la representación gráfica de los desplazamientos X (Norte-Sur), Y (Oeste-Este) y Z (Vertical) en función del tiempo en la fecha (año, mes, día, hora y minuto) dada por UTC (Coordinated Universal Time) que es el estándar de tiempo. Es sinónimo de GMT (Greenwich Mean Time). En la página web de Wikipedia Tiempo Universal Coordinado se explica que es UTC y las zonas horarias respecto a UTC, pero esto no es importante para el análisis de los datos.
La figura (la original es más larga) muestra parcialmente el registro del desplazamiento vertical Z de las olas que van llegando a la boya situada en esta estación, el día 26 de marzo desde las 20:15:00 hasta las 20:45:00 hora UTC.
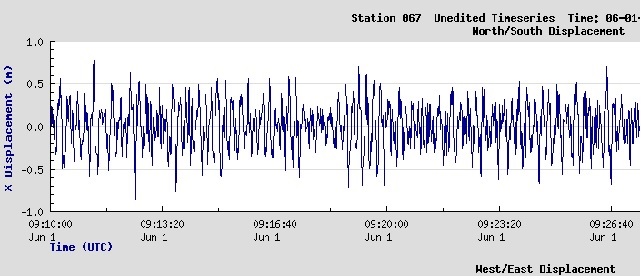
Pulsando el botón View data vemos los datos correspondientes a los gráficos. Si deseamos descargar los datos nos tenemos que fijar en el último campo de la cabecera. Error-free vectors: 100.0%. Si no marca el 100.0% quiere decir que faltan datos y seleccionamos en la parte superior otra fecha UTC hasta encontrar un fichero completo.
Cabecera
Station: 06701 Deployment latitude: 33 13.241' N Deployment longitude: 119 52.889' W Water depth(m): 335.28 Local magnetic variation(deg): 13 E Data type: Datawell vectors Gauge type: Datawell Mark 3 directional buoy Sample rate(Hz): 1.280 Field software version: datawell_acq v2 Field station type: sun Method of analysis: Datawell GPS: yes Start time: 20140326201500 UTC End time: 20140326204459 UTC Sample length(hh:mm:ss): 00:30:00 Total number of vectors: 2304 Error-free vectors: 100.0% -----------------------------
La cabecera contiene información básica acerca del sensor: la posición, la frecuencia de muestreo, el tipo de boya, el tiempo inicial y final de la toma de datos, el número de datos y si están todos los datos 100.0% o se han perdido algunos de ellos. Para nuestro análisis los campos más importantes están marcados en letra negrita.
La correspondencia entre los datos es la siguiente. La frecuencia de muestreo es fs=1.280 Hz, por lo que el intervalo de tiempo entre dos medidas consecutivas es Δt=1/fs=1/1.280 s. Se han tomado muestras durante T0=30 minutos, o 1800 s, por lo que el número total de datos es N=30·60·1.280=2304.
Los datos
Los datos vienen en cuatro columnas:
- El tiempo UTC, en el formato YYYYMMDDhhmmss (Año, mes, día, hora, minuto, segundo)
- El desplazamiento en centímetros en la dirección Norte-Sur, Norte es positivo.
- El desplazamiento en centímetros en la dirección Oeste-Este, Oeste es positivo.
- El desplazamiento vertical Z en centímetros
| YYYYMMDDhhmmss | X(cm) | Y(cm) | Z(cm) |
| 20140326201500 | 42 | 56 | -48 |
| 20140326201501 | 37 | 38 | -12 |
| 20140326201502 | 9 | 20 | -8 |
| 20140326201502 | -18 | 33 | -34 |
| ..... | ... | ... | ... |
| 20140326204457 | 15 | 57 | 36 |
| 20140326204458 | -29 | 20 | 63 |
| 20140326204458 | -53 | -12 | 71 |
| 20140326204459 | -43 | -46 | 63 |
Preparación de los datos
Seleccionamos en la página web los datos con el puntero del ratón, los copiamos y los pegamos en un documento nuevo Microsoft Word. Eliminamos la cabecera del fichero, dejando solamente las cuatro columnas de datos. Manteniendo pulsada la tecla Alt, con el ratón seleccionamos las tres primeras columnas y las eliminamos (cortar), quedando solamente la columna Z del desplzamiento vertical de las olas del mar en cm. Guadamos el texto sin formato en una carpeta accesible a MATLAB con el nombre olasZ.txt que se descarga en este enlace.
Importamos el fichero de datos
>> z=olasZ-mean(olasZ); >> mean(z) ans = -8.5117e-016 >> clear olasZ
La estadística básica es el número de elementos del vector, la desviación estándar, el valor máximo y mínimo
>> length(z) ans = 2304 >> std(z) ans = 65.7688 >> max(z) ans = 214.9002 >> min(z) ans = -204.0998
Representamos los primeros 500 datos de los desplazamientos z en función del tiempo t.
Si t=0, es el tiempo en el que se ha tomado el primer dato, los instantes t en el que se ha tomado las sucesivas medidas del desplazamiento z de calculan del siguiente modo:
>> t=(0:length(z)-1)/1.28;
Siendo fs=1.280 Hz, la frecuencia de muestreo o Δt=1/fs=1/1.280 s. el intervalo de tiempo entre dos medidas consecutivas.
>> z=olasZ-mean(olasZ);
>> clear olasZ
>> t=(0:length(z)-1)/1.28;
>> plot(t,z)
>> xlabel('tiempo (s)')
>> ylabel('Desplazamiento (cm)')
>> title('Olas')
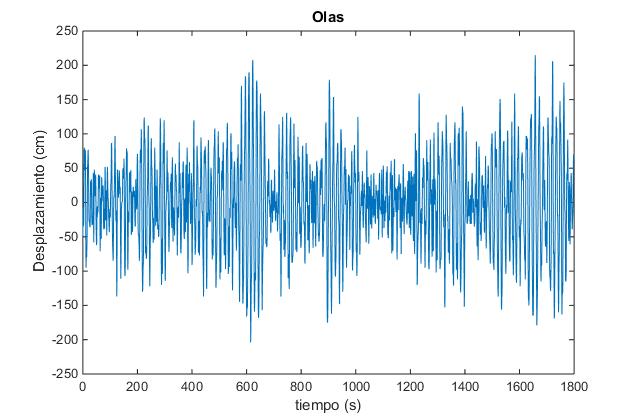
Utilizando los iconos Zoom y Pan bajo el menú de la ventana gráfica podemos seleccionar y ampliar, para ver con más detalle, los intervalos de tiempo en los que estemos más interesados.
Ajuste a la función de distribución de Gauss
Vamos a agrupar los datos en intervalos de anchura 20 cm
Por ejemplo, los datos de los desplazamientos verticales Z de las olas comprendidos en el intervalo entre -10 a 10 cm se representan mediante una barra centrada en 0 cuya altura es proporcional al número de datos que caben en dicho intervalo y se puede obtener mediante el siguiente comando.
>> sum(z>=-10 & z<10) ans = 297
Los datos de los desplazamientos verticales Z de las olas comprendidos entre 10 y 30 cm se representan mediante una barra centrada en 20 cm, cuya altura es proporcional al número de datos que caben en dicho intervalo y se puede obtener mediante el siguiente comando.
>> sum(z>=10 & z<30) ans = 276
La función hist realiza la tarea completa y devuelve el número de datos que caben en cada intervalo y el centro de cada intervalo.
>> x=-220:20:220; >> [num,center]=hist(z,x) num = 0 1 5 25 34 57 80 150 149 226 267 297 276 242 170 144 77 49 20 19 10 5 1 center = -220 -200 -180 -160 -140 -120 -100 -80 -60 -40 -20 0 20 40 60 80 100 120 140 160 180 200 220
Como podemos apreciar, al intervalo centrado en 0 y de anchura 20 cm le corresponde 297 medidas y al intervalo centrado en 20 cm le corresponden 276 medidas.
La altura de la barra la calculamos mediante la siguiente fórmula
Donde Ni es el número de desplazamientos que caben en el intervalo i, y Δx=20 cm es la anchura de cada intervalo. N=2304 es el número total de datos. La razón de dividir entre Δx es que la suma de las áreas de todas las barras de anchura Δx debe dar la unidad.
Ajustamos los datos a la función de distribución de Gauss.
Como podemos comprobar con Math Symbolic el área bajo la curva es la unidad
>> syms a positive;
>> syms x;
>> int('exp(-x^2/(2*a^2))/(sqrt(2*pi)*a)',x,-inf,inf)
ans =1
Creamos un script que realice las siguientes tareas:
Cargue mediante el comando
load el ficheroolasZ.txt de los datos de las alturas registradas de las olas del mar.Cree un vector de desplazamientos verticales
z de las olas cuya media sea cero, para ello se resta a cada dato de desplazamiento el valor medio.Sabiendo que el valor máximo es 214.9 y el valor mínimo -204.0998 cm de las alturas, se agrupan los datos de los desplazamientos en intervalos de 20 cm de anchura desde -220 cm a 220 cm
A partir del número de datos Ni en cada intervalo i determinamos la altura p(xi) de cada una de las barras de anchura Δx.
Utilizando la función
nlinfit para realizar el ajuste de los datos p(xi) a una función que que depende de un parámetro σ. La funciónnlinfit devuelve el valor del parámetro σ (en el códigoaf ) de la funciónf (x) que mejor ajusta a los datos. Como podemos comprobar el valor af es próximo a la desviación estandar std(z) de los datos de los desplazamientos z.Represente en la misma ventana gráfica el diagrama de barras p(xi) y la función de distribución de Gauss f(x) que mejor ajusta a los datos..
load olasZ.txt;
z=olasZ-mean(olasZ);
clear olasZ
%tabla de frecuencias
x=-220:20:220;
num=hist(z,x);
frec=num/(sum(num)*20);
%ajuste a la función de distribución de Gauss
f=@(a,x) exp(-x.^2/(2*a^2))/(sqrt(2*pi)*a);
a0=std(z); %valor inicial del parámetro
af=nlinfit(x,frec,f,a0)
hold on
%diagrama de frecuencias
bar(x,frec,'c');
%representa la curva de ajuste
x=linspace(-200,200,100);
y=f(af,x);
plot(x,y,'r')
title('Ajuste a la función de Gauss')
xlabel('Desplazamiento')
ylabel('Frecuencia')
hold off
title('Desplazamiento de las olas del mar')
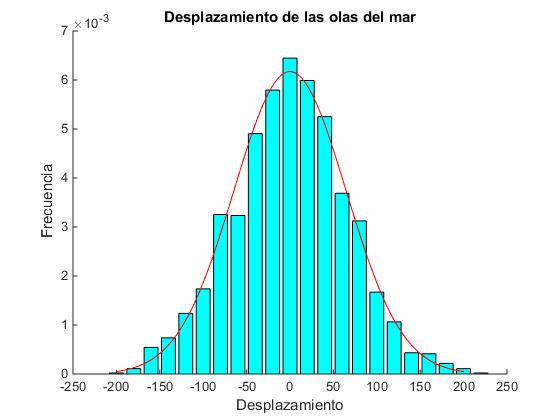
af = 64.6194 %parámetro de ajuste (sigma) >> std(z) %desviación estándar ans = 65.7688

