Análisis armónico de las mareas.
El ciclo de marea se producen habitualmente dos veces al día (dos pleamares y dos bajamares). Sin embargo, hay localidades donde se producen una vez al día (muy pocos sitios) y otras localidades en las que son mixtas..
En el mapa que aparece en la página web NOAA ocean service education vemos que en Europa las mareas son del primer tipo, denominadas semidiurnas.
Hemos dado una explicación simple de las mareas en base a dos componentes: uno de periodo 12.42 h y otro de periodo 12.0 horas.
t=0:30*24;
yL=0.53*cos(2*pi*t/12.42);
yS=0.24*cos(2*pi*t/12.0);
subplot(2,1,1)
plot(t,yL,'b',t,yS,'r')
xlim([0,30*24])
ylim([-1,1])
xlabel('hora')
ylabel('altura')
legend ('M2','S2');
subplot(2,1,2)
plot(t,yL+yS,'k')
xlim([0,30*24])
ylim([-1,1])
xlabel('hora')
ylabel('altura')
legend ('M2+S2');
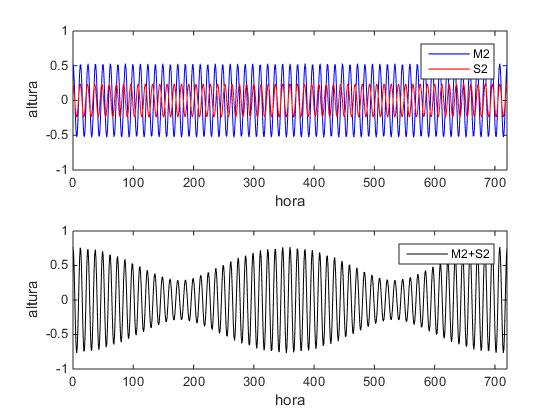
Las mareas vivas se producen cuando la altura es máxima y las mareas muertas cuando la altura es mínima.
Los datos de las amplitudes 0.53 y 0.24 se han tomado de la descripción cualitativa del fenómeno de las mareas
Hay otros factores que complican la descripción de las mareas:
- El eje de la Tierra está inclinado 23.5° respecto de la perpendicular al plano de la eclíptica y esto hace que el ángulo formado por el plano ecuatorial y el plano de la eclíptica varíe en ±23.5° a lo largo del año, la declinación da lugar a los tres tipos de marea mencionados.
- La órbita de la Luna alrededor de la Tierra es elíptica, por lo que la distancia entre la Tierra y la Luna no es constante
- La órbita de la Tierra alrededor del Sol es elíptica, por lo que la distancia entre la Tierra y el Sol no es constante.
Los contituyentes básicos de las mareas además de los dos descritos son los siguientes:
| Símbolo | Periodo (horas) | Descripción |
|---|---|---|
| M2 | 12.42 | Constituyente principal, mareas semidiurnas, debido a la Luna |
| S2 | 12.00 | Constituyente principal, mareas semidiurnas, debido al Sol |
| N2 | 12.66 | Debido a la variación de la distancia entre la Tierra y la Luna |
| K2 | 11.97 | Debido a los cambios de declinación del Sol y la Luna |
| K1 | 23.93 | Solar-lunar |
| O1 | 25.82 | Constituyente principal, mareas diurnas, debido a la Luna |
| P1 | 24.07 | Constituyente principal, mareas diurnas, debido a la Luna |
A estos constituyentes se pueden añadir muchos más tal como puede verse en la página Harmonic constituents en la que se porporciona la lista de armónicos empleados para la predicción de las mareas en diversas localidades de Estados Unidos. E
Altura del nivel del mar
En la web Red de Información de datos Oceanográficos (http://indamar.ieo.es/) se dispone de acceso a datos sobre el nivel del mar, pulsando en el enlace Acceso a datos en la barra horizontal y a continuación en el enlace Sea Level Data.
En primer lugar, elegimos en el cuadro Datos y gráficos recientes, Santander y pinchando sobre el gráfico, vemos el de la variación de la altura del nivel del mar entre el 1 de julio y el 16 de julio de 2013. Un gráfico que vamos a reproducir a partir de los datos que se obtienen pinchando en datos.
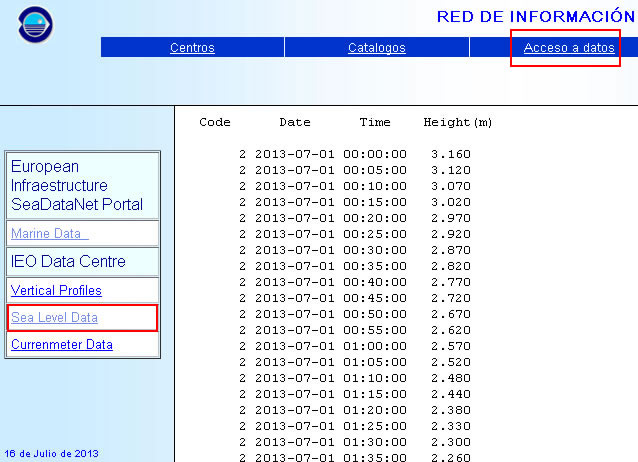
Vemos en la última columna los datos de la altura del nivel del mar en metros recogidos desde las 0 horas del día 1 de julio de 2013 hasta las 8 horas 35 minutos de día 16 de julio, medidos cada cinco minutos..
La web es antigua y utiliza frames por lo que no se pueden guardar los datos eligiendo en el menú del navegador Guardar como... Es necesario seleccionar los datos con el cursor y pulsar la combinación de teclas Ctrl+C, para copiar los datos.
Se abre el procesador de texto Word y se pegan o se pulsa la combinación de teclas Ctrl+V.
Con la combinación Alt+cursor borramos las cuatro primeras columnas manteniendo la columna de alturas (Height). Seleccionamos en el menú Archivo Guardar como.. ponemos el nombre del archivo y a continuación en Guardar como tipo, seleccionamos Texto sin formato, al pulsar el botón Guardar aceptamos la opción Windows (predeterminada).
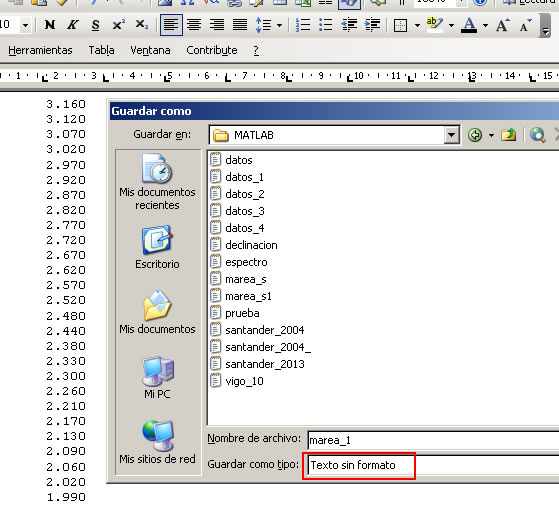
Antes de analizar una serie temporal de datos, hemos de inspeccionarlos cuidadosamente ya que algunas series no están completas.
Para realizar un análisis de los datos seguimos el mismo procedimiento que empleamos para el análisis de las manchas solares en el capítulo dedicado a la Transformada de Fourier.
Situamos el fichero marea_1.txt que se puede descargar en este enlace, en la carpeta de ficheros accesible a MATLAB.
Realizamos la representación gráfica de los datos, en el eje vertical el nivel del mar en metros, en el eje horizontal el tiempo en horas.
>> load marea_1.txt
>> t=(0:length(marea_1)-1)*5/60; %el nivel del mar se mide cada cinco minutos
>> plot(t,marea_1)
>> xlabel('hora')
>> ylabel('Nivel del mar (m)')
>> title('Altura de las mareas')
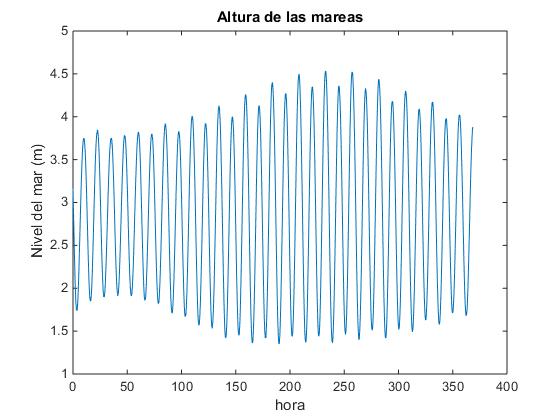
Utilizamos Zoom y Data cursor para medir la distancia horizontal entre dos picos consecutivos, para medir el periodo.
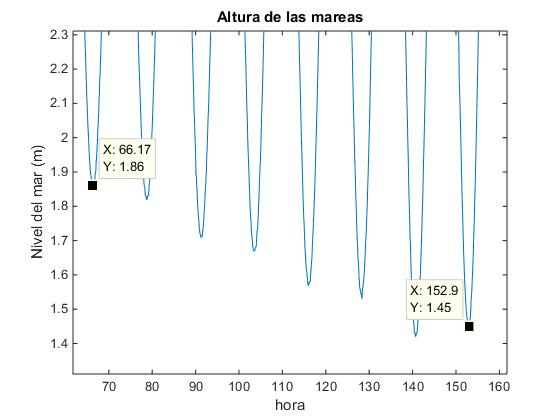
Medimos las abscisas del primero y último pico que vemos en la ventana gráfica y calculamos el espaciado medio entre picos (152.9-66.17)/7=12.39.
Otro dato interesante es el nivel medio del mar en el periodo estudiado
>> mean(marea_1)
ans =
2.8614
Antes de aplicar
transformada de
Fourier tenemos que substraer la tendencia lineal de los datos (si existe) para lo que podemos utilizar la función
Representamos gráficamente el nivel del mar en función del tiempo en horas y realizamos la Transformada Rápida de Fourier, representando en el eje vertical la potencia y en el horizontal las frecuencias. Fijarse que el intervalo de tiempo entre dos medidas consecutivas es dt=5 minutos=5/60 horas.
load marea_1.txt
t=(0:length(marea_1)-1)*5/60; %el nivel del mar se mide cada cinco minutos
plot(t,marea_1)
xlabel('hora')
ylabel('Nivel del mar')
title('Altura de las mareas')
f=detrend(marea_1);
n=length(f);
dt=5/60; %cinco minutos
dw=2*pi/(n*dt);
w=(0:n-1)*dw;
wc=pi/dt; %frecuencia angular crítica
g=fft(f);
power=abs(g).^2;
figure
stem(w,power,'markersize',4,'markerfacecolor','r')
xlim([0 2])
indice=find(power==max(power));
periodo=2*pi/w(indice(1))
text(w(indice(1))+.1,power(indice(1)), ['periodo',num2str(periodo)]);
xlabel('frecuencia')
ylabel('Potencia')
title('Espectro de frecuencias')
Observamos un pico muy elevado situado en ω=0.51129, lo que da un periodo P=2π/ω=12.2889 horas, tal como observamos en la ventana gráfica al lado de la frecuencia predominante.
Utilizando Zoom y Pan podemos ver con más detalle el espectro de frecuencias