Las fórmulas con la que MATLAB calcula la transformada rápida de Fourier Y=fft(x) y la transformada inversa y=ifft(X) son, respectivamente:

${\displaystyle \begin{array}{l}X(k)={\displaystyle \sum _{j=1}^{N}x(j){\omega }_N^{(j-1)(k-1)}}\\ x(j)=\frac{1}{N}{\displaystyle \sum _{k=1}^{N}x(k){\omega }_N^{-(j-1)(k-1)}}\end{array}\}{\omega }_N=\exp \left(-\frac{2\pi i}{N}\right)}$

Supongamos que tenemos una señal descrita por un conjunto de n (potencia de dos) pares de datos (t_j,x_j) igualmente espaciados en el tiempo, por un intervalo Δt, desde t=0 hasta t_final=(n-1)Δt. La inversa del intervalo Δt, se denomina frecuencia de muestreo f_s. De modo que el vector de tiempos es t=(0:n-1)/ f_s

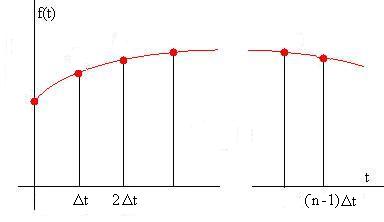
La función fft de MATLAB convierte un vector de valores de la señal x en función del tiempo t en un vector g en función de la frecuencia ω.

g=fft(x)

g es un vector cuyos elementos son números complejos por que guarda información acerca de de la amplitud y de la fase. Ahora tenemos que asociar cada elemento del vector g con una frecuencia, del mismo modo que hemos asociado cada elemento del vector x con un tiempo.

El intervalo de frecuencias es Δω=2π/(n·Δt)=2πf_s/n de modo que la mínima frecuencia es 0 y la máxima ω_max=2πf_s(n-1)/n. La resolución espectral Δω es inversamente proporcional al tiempo total n·Δt de recogida de datos en la serie temporal.

Conocido el intervalo de tiempo Δt o la frecuencia de muestreo Δt=1/f_s y el número de pares de datos n (potencia de 2), creamos el vector de tiempos t y el vector de frecuencias angulares ω del siguiente modo:

>> n=length(x);
>> t=(0:n-1)*dt;
>> dw=2*pi/(n*dt);
>> w=(0:n-1)*dw;

Podemos obviar la fase y concentrarnos en la amplitud, si calculamos y representamos el cuadrado de los elementos del vector g. A P se le denomina espectro de potencia (Power spectrum)

${\displaystyle P={\left|g(\omega )\right|}^2}$

Para ilustrar la aplicación de la función fft de MATLAB, vamos a analizar la señal formada por la suma de cuatro armónicos de frecuencias angulares ω=1, 3, 3.5, 4 y 6 rad/s

x(t)=cos(t)+0.5·cos(3t)+0.4·cos(3.5t)+0.7·cos(4t)+0.2·cos(6t)

Recuérdese que la transformada de Fourier de f(t)=cos(ω₀t) es F(ω)=π[δ(ω-ω₀)+δ(ω+ω₀)]. Dos funciones delta de Dirac situados en +ω₀ y en -ω₀.

Creamos un script para realizar las siguientes tareas:

1. Construir una serie temporal (x,t) formada por n=2¹⁴=16384 pares de datos, tomando un intervalo de tiempo Δt=0.4 s, o bien una frecuencia de muestreo de f_s=2.5 Hz. El tiempo final es t_final=16383·0.4=6553.2 s
2. Calcular la transformada rápida de Fourier fft y la guardamos en el vector g
3. Crear el array de frecuencias ω como en el cuadro anterior
4. Calculamos la potencia power: el cuadrado del valor absoluto de cada elemento de g.
5. Representar gráficamente power en términos de la frecuencia angular ω

%serie temporal
n=2^14;
dt=0.4;
t=(0:n-1)*dt; %vector de tiempos
x=cos(t)+0.5*cos(3*t)+0.4*cos(3.5*t)+0.7*cos(4*t)+0.2*cos(6*t);

%amplitud-fase vs. frecuencias
g=fft(x);
power=abs(g).^2;
dw=2*pi/(n*dt);
w=(0:n-1)*dw; %vector de frecuencias angulares

plot(w,power)
xlabel('\omega')
ylabel('P(\omega)')
title('Espectro de potencia')

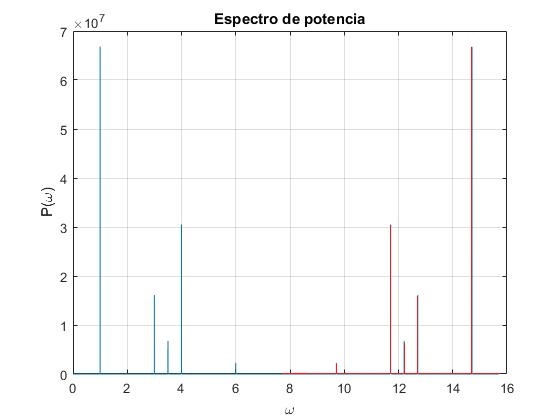
La transformada de Fourier de la función x(t) superposición de cinco funciones armónicas nos debería dar funciones delta δ(ω) de altura infinita situadas en ω=±ω₀. El resultado de la aplicación de la función fft de MATLAB es un conjunto de picos muy estrechos y de gran amplitud.

La transformada de Fourier de cualquier señal tiene un número igual de frecuencias positivas que negativas, P(ω)=P(-ω). En la ventana de la representación gráfica vemos solamente frecuencias positivas, no vemos la parte negativa del espectro. En la figura de más abajo, vemos las componentes de frecuencias negativas en color rojo.

%serie temporal
n=2^14;
dt=0.4;
t=(0:n-1)*dt; %vector de tiempos
x=cos(t)+0.5*cos(3*t)+0.4*cos(3.5*t)+0.7*cos(4*t)+0.2*cos(6*t);

%amplitud-fase vs. frecuencias
y=fft(x);
g=fftshift(y);
power=abs(g).^2;
dw=2*pi/(n*dt);
w=(-n/2:n/2-1)*dw;

plot(w,power)
xlabel('\omega')
ylabel('P(\omega)')
grid on
title('Espectro de potencia')

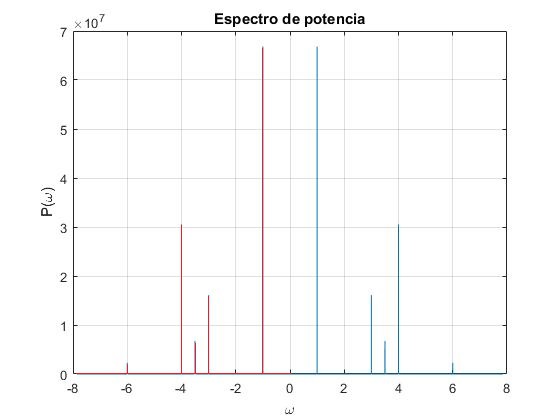
Así pues, solamente la primera mitad de la ventana gráfica muestra los picos de frecuencias correctas, la otra mitad corresponde a las frecuencias negativas.

Solamente podemos detectar los componentes de frecuencia que son menores que ω_c=π/Δt=πf_s. Esta frecuencia límite se denomina frecuencia crítica o frecuencia de Nyquist. En el ejemplo anterior, ω_c=7.85 rad/s. Luego, todas las frecuencias de los armónicos componentes de la señal, ω=1, 3, 3.5, 4 y 6 rad/s son detectadas.

Si solamente queremos ver las frecuencias positivas hasta la frecuencia angular crítica ω_c, modificamos el script :

n=2^14;
dt=0.4;
t=(0:n-1)*dt; %vector de tiempos
x=cos(t)+0.5*cos(3*t)+0.4*cos(3.5*t)+0.7*cos(4*t)+0.2*cos(6*t);

%amplitud-fase vs. frecuencias
g=fft(x);
power=abs(g).^2;
dw=2*pi/(n*dt);
w=(0:n-1)*dw; 
wc=pi/dt; %frecuencia angular crítica
plot(w,power)
xlim([0 wc])

xlabel('\omega')
ylabel('P(\omega)')
grid on
title('Espectro de potencia')

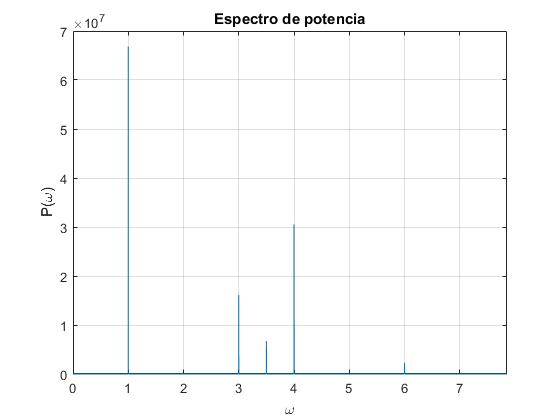
Si queremos distinguir entre dos frecuencias ω₁ y ω₂ en el espectro es necesario que Δω<<|ω₁-ω₂| sea pequeño por lo que el tiempo total de muestreo de la señal n·Δt deberá ser grande. Si queremos que frecuencia crítica ω_c sea grande entonces Δt tendrá que ser pequeño o la frecuencia de muestreo f_s grande. En cualquier caso, tendremos que procesar muchísimos datos n.

Efecto de la frecuencia de muestreo f_s

Supongamos la siguiente función y su transformada de Fourier

${\displaystyle \begin{array}{l}f(t)=t\exp (-t)\\ F(\omega )={\displaystyle \underset{-\infty }{\overset{\infty }{\int }}f(t)\exp (-i\omega t)dt=}\\ {\displaystyle \underset{0}{\overset{\infty }{\int }}t\exp (-t)\exp (-i\omega t)dt=}{\displaystyle \underset{0}{\overset{\infty }{\int }}t\exp (-at)dt=}\\ {-\frac{1}{a}\left(t+\frac{1}{a}\right)\exp (-at)|}_0^{\infty }=\frac{1}{a^2}=\frac{1}{{\left(1+i\omega \right)}^2}\end{array}}$

Para estudiar el efecto la frecuencia de muestreo f_s en la Transformada Rápida de Fourier, vamos a tomar n=16 datos igualmente espaciados de la función f(t) tomando una frecuencia de muestreo f_s=2 Hz, es decir Δt=1/f_s=0.5 s es el intervalo de tiempo entre dos muestras consecutivas de f(t). El último dato corresponde al instante (n-1)Δt=15·0.5=7.5 s La frecuencia crítica ω_c=π/Δt=πf_s=2π.

fs=2; %frecuencia de muestreo
n=16; %número de datos
dt=1/fs;
t=(0:n-1)*dt;
x=t.*exp(-t); %muestras, datos

subplot(2,1,1)
tt=0:0.05:8;
xx=tt.*exp(-tt);
plot(tt,xx,'b',t,x,'ro','markersize',4,'markeredgecolor','r',
'markerfacecolor','r')
xlabel('t')
ylabel('x')
title('f(t)')

subplot(2,1,2)
wc=pi*fs; %frecuencia límite de Nyquist
ww=-4*pi:0.1:4*pi;
Fw=1./(1+1i*ww).^2;

%transformada rápida de Fourier
y=fft(x,n);
g=fftshift(y);
dw=2*pi/(n*dt);
w=(-n/2:n/2-1)*dw;

plot(ww,abs(Fw),'b',w,abs(g)/fs,'ro','markersize',3,'markeredgecolor','r',
'markerfacecolor','r')
set(gca,'XTick',-4*pi:2*pi:4*pi)
set(gca,'XTickLabel',{'-4\pi','-2\pi','0','2\pi','4\pi'})
xlim([-4*pi,4*pi])
xlabel('\omega')
ylabel('|F(w)|')
title('Transformada')

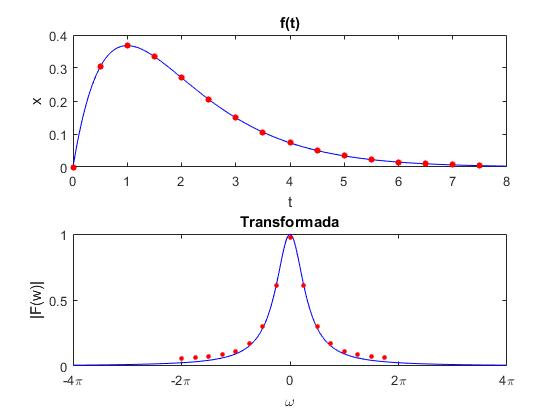
Cambiamos la frecuencia de muestreo a f_s=16 Hz, es decir Δt=1/f_s=0.0625 s es el intervalo de tiempo entre dos muestras consecutivas de f(t). El número n=128 de datos, por lo que el último dato corresponde al instante (n-1)Δt=127·0.0625=7.9375 s. La frecuencia crítica ω_c=π/Δt=πf_s=16π.

fs=16; %frecuencia de muestreo
n=128; %número de datos
.............

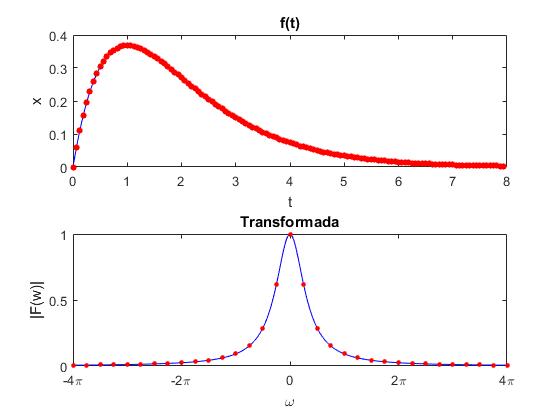
Las frecuencias ω se extienden desde -16π a +16π, pero se muestran de -4π a +4π para comparar con el ejemplo previo.

Función de Gauss

Hemos estudiado en la página titulada "Propagación de las ondas en un medio dispersivo" la transformada de Fourier de la función cos(ω₀t) modulada por una función de Gauss.

${\displaystyle \begin{array}{l}f(t)=\exp \left(-\frac{{\left(t-t_0\right)}^2}{2{\sigma }^2}\right)\cos \left({\omega }_{0}t\right)\\ F(\omega )=\sqrt{2\pi }\sigma \exp \left(i{\omega }_0{t}_0\right)\exp \left(-i\omega t_0\right)\exp \left(-\frac{{\left(\omega -{\omega }_0\right)}^2{\sigma }^2}{2}\right)\\ +\sqrt{2\pi }\sigma \exp \left(-i{\omega }_0{t}_0\right)\exp \left(-i\omega t_0\right)\exp \left(-\frac{{\left(\omega +{\omega }_0\right)}^2{\sigma }^2}{2}\right)\end{array}}$

La transformada de Fourier no se ve afectada por la posición del centro del pulso t₀.

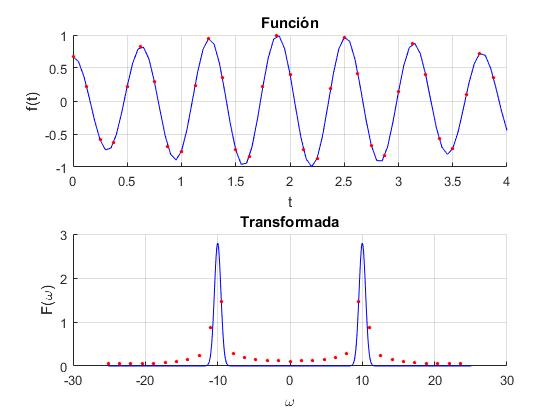
En primer lugar, centramos el pulso en t₀=8 y establecemos la anchura del pulso en σ²=5, tomamos ω₀=10 como frecuencia angular. Dibujamos la función f(t) en el intervalo 0<t<16. Aunque el pulso se extiende desde -∞ a +∞, en el intervalo [0,16] está definido el pulso.

Con una frecuencia de muestreo f_s=8, tomamos n=128 datos, señalamos los datos tomados como puntos de color rojo en la gráfica f(t). El primer dato corresponde al instante t₁=0 y el último dato al instante t_n=(n-1)/ f_s=127/8=15.875

En la parte inferior de la ventana, representamos la transformada de Fourier F(ω) en el intervalo comprendido entre -ω_c y ω_c , siendo ésta la fecuencia límite ω_c=πf_s. Calculamos la transformada rápida de Fourier (FFT) de los datos tomados y representamos su módulo en dicho intervalo.

t0=8;
w0=10;
s2=5;
t=0:0.05:16;
f=@(t) exp(-(t-t0).^2/(2*s2)).*cos(w0*t);

subplot(2,1,1)
hold on
plot(t,f(t),'b')
fs=8;
n=128;
dt=1/fs;
t=(0:n-1)*dt;
ft=f(t);
plot(t,ft,'ro','markersize',2,'markeredgecolor','r','markerfacecolor','r')
hold off
grid on
xlabel('t')
ylabel('f(t)')
title('Función')

subplot(2,1,2)
hold on
wc=pi*fs; %frecuencia límite de Nyquist
w=-wc:0.1:wc;
Fw=sqrt(2*pi*s2)*exp(-1i*w*t0).*(exp(1i*w0*t0)*exp(-(w-w0).^2*s2/2)+...
exp(-1i*w0*t0)*exp(-(w+w0).^2*s2/2))/2;

%transformada rápida de Fourier
y=fft(ft,n);
g=fftshift(y);
dw=2*pi/(n*dt);
ww=(-n/2:n/2-1)*dw;
plot(w,abs(Fw),'b',ww,abs(g)/fs,'ro','markersize',2,
'markeredgecolor','r','markerfacecolor','r')
hold off
grid on
xlabel('\omega')
ylabel('F(\omega)')
title('Transformada')

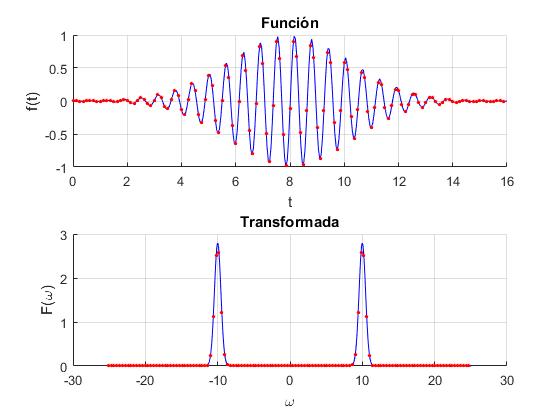
Obtenemos dos picos situados en ω=-ω₀=-10 y ω=+ω₀=10

Si ahora centramos el pulso en t₀=2 y tomamos n=32 datos con la misma frecuencia de muestreo f_s=8, de modo que el primer dato corresponde al instante t₁=0 y el último dato al instante t_n=(n-1)/ f_s=31/8=3.875, obtenemos una pobre definición de la transformada de Fourier tal como puede verse en la parte inferior de la figura.

t0=2;
w0=10;
s2=5;
t=0:0.05:4;
f=@(t) exp(-(t-t0).^2/(2*s2)).*cos(w0*t);

subplot(2,1,1)
hold on
plot(t,f(t),'b')
fs=8;
n=32;
dt=1/fs;
t=(0:n-1)*dt;
ft=f(t);
plot(t,ft,'ro','markersize',2,'markeredgecolor','r','markerfacecolor','r')
hold off
grid on
xlabel('t')
ylabel('f(t)')
title('Función')

subplot(2,1,2)
hold on
wc=pi*fs; %frecuencia límite de Nyquist
w=-wc:0.1:wc;
Fw=sqrt(2*pi*s2)*exp(-1i*w*t0).*(exp(1i*w0*t0)*exp(-(w-w0).^2*s2/2)+...
exp(-1i*w0*t0)*exp(-(w+w0).^2*s2/2))/2;

%transformada rápida de Fourier
y=fft(ft,n);
g=fftshift(y);
dw=2*pi/(n*dt);
ww=(-n/2:n/2-1)*dw;
plot(w,abs(Fw),'b',ww,abs(g)/fs,'ro','markersize',2,'markeredgecolor','r',
'markerfacecolor','r')
hold off
grid on
xlabel('\omega')
ylabel('F(\omega)')
title('Transformada')