Serie finita de Fourier

Supongamos que medimos la elevación del nivel del mar en función del tiempo en una determinada posición a medida que van pasando las olas. Una boya situada en dicha posición registra los cambios de altura y las transmite cada cierto tiempo al centro oceanográfico.

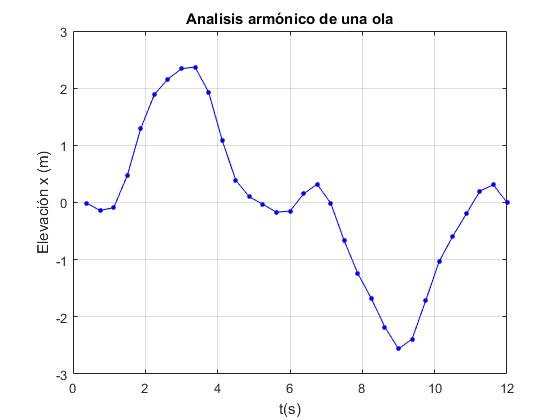
Supongamos que hemos registrado las medidas durante un tiempo P=12 segundos y se han transmitido los datos cada Δt=0.375 s, en total N=32 datos. Su representación gráfica es la siguiente

xk=[-0.01,-0.14,-0.09,0.47,1.3,1.89,2.16,2.34,2.37,1.93,1.09,0.39,
0.1,-0.03,-0.17,-0.15,0.15,0.32,-0.01,-0.67,-1.24,-1.68,-2.18,-2.56,
-2.39,-1.72,-1.03,-0.59,-0.2,0.2,0.31,0.0];
N=length(xk);
dt=0.375; %intervalo de tiempo
tk=(1:N)*dt;
plot(tk,xk,'-o','markersize',4,'markerfacecolor','r')
grid on
xlabel('t(s)')
ylabel('Elevación x (m)')
title ('Analisis armónico de una ola')

La serie finita de Fourier se escribe

${\displaystyle \begin{array}{l}x(t)=a_0+{\displaystyle \sum _{j=1}^{N/2}{a}_j\cos \left(\frac{2\pi j}{P}t\right)}+{\displaystyle \sum _{j=1}^{N/2-1}{b}_j\sin \left(\frac{2\pi j}{P}t\right)}\\ a_0=\frac{1}{N}{\displaystyle \sum _{k=1}^N{x}_k}\\ a_j=\frac{2}{N}{\displaystyle \sum _{k=1}^N{x}_k·\cos \left(\frac{2\pi k}{N}j\right)}j=\mathrm{1,2,3...}\frac{N}{2}-1\\ a_{N/2}=\frac{1}{N}{\displaystyle \sum _{k=1}^N{x}_k\cos \left(k\pi \right)}\\ b_j=\frac{2}{N}{\displaystyle \sum _{k=1}^N{x}_k·\sin \left(\frac{2\pi k}{N}j\right)}j=\mathrm{1,2,3...}\frac{N}{2}-1\end{array}}$

Donde x_k es la medida de la altura x en el instante t_k. Al final de esta página, justificamos las fórmulas que que nos permiten calcular los coeficientes a_j y b_j

Amplitudes

Calculamos los coeficientes a₀, de a₁ a a_N/2-1, de b₁ a b_N/2-1 y a_N/2.Con estos coeficientes dibujamos la función x(t), junto a los datos (t_k,x_k) k=1,2...N experimentales.

xk=[-0.01,-0.14,-0.09,0.47,1.3,1.89,2.16,2.34,2.37,1.93,
1.09,0.39,0.1,-0.03,-0.17,-0.15,0.15,0.32,-0.01,-0.67,-1.24,-1.68,
-2.18,-2.56,-2.39,-1.72,-1.03,-0.59,-0.2,0.2,0.31,0.0];
N=length(xk);
dt=0.375; %intervalo de tiempo
tk=(1:N)*dt;

a0=sum(xk)/N;
a=zeros(1,N/2);
b=zeros(1,N/2);
k=1:N;
for i=1:N/2-1
    a(i)=sum(xk.*cos(2*pi*i*k/N))*2/N;
    b(i)=sum(xk.*sin(2*pi*i*k/N))*2/N;
end
a(N/2)=sum(xk.*cos(pi*k))/N;

figure
subplot(2,2,1)
stem(a);
xlabel('Armónico')
ylabel('a(i)')

subplot(2,2,2)
stem(b);
xlabel('Armónico')
ylabel('b(i)')

subplot(2,2,3:4) %resultante
t=(0:0.01:12); %segundos
x=zeros(1,length(t));
w0=2*pi/(N*dt);
x=a0;
for i=1:N/2
    x=x+a(i)*cos(i*w0*t)+b(i)*sin(i*w0*t);
end
hold on
plot(t,x,'b')
plot(tk,xk,'bo','markersize',3,'markerfacecolor','b')
hold off
grid on
xlabel('t')
ylabel('x')
title('Resultante')

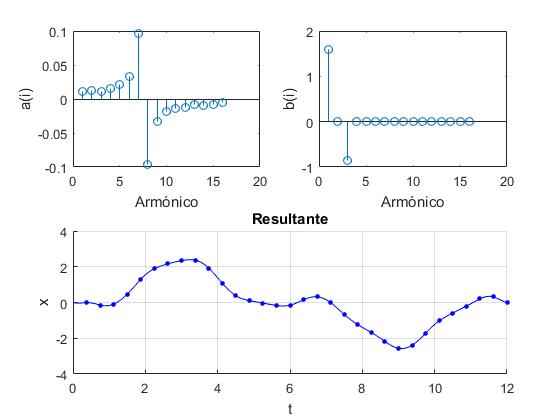
Como vemos en las dos gráficas de la parte de arriba, los coeficientes b_j que nos son cero corresponden al primer armónico j=1 cuya frecuencia es f₁=1/P=1/12=0.0833 Hz y el tercer armónico cuya frecuencia es f₃= 3·f₁=0.25 Hz. Los coeficientes a_j son próximos a cero excepto los que corresponden a las frecuencias f₇ y f₈.

La frecuencia más alta f_c que se puede detectar cuando se toman N datos separados un intervalo de tiempo Δt es

${\displaystyle f_c=\frac{N}{2}{f}_1=\frac{1}{2\Delta t}}$

a esta frecuencia se le denomina de Nyquist, que en este ejemplo es f₁₆=16·f₁=1/(2·0.375)=1.333 Hz

Energía

La energía de un oscilador es proporcional al cuadrado de la amplitud.

${\displaystyle \begin{array}{l}\Delta f=\frac{1}{N·\Delta t}\\ S(i)=\frac{1}{2}\frac{\left(a_i^2+b_i^2\right)}{\Delta f}i=\mathrm{1,2,3...}\frac{N}{2}\end{array}}$

El intervalo de frecuencias Δf=1/P es la diferencia entre dos frecuencias consecutivas

La energía total es el área bajo la curva

${\displaystyle E={\displaystyle \sum _{i=1}^{N/2}S(i)·\Delta f}}$

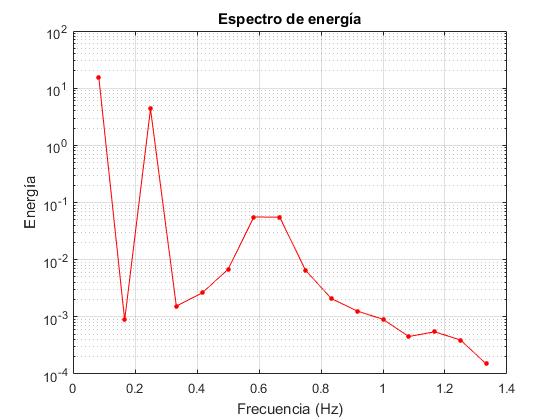
Representamos la energía en función de la frecuencia en escala logarítmica en el eje Y.Con Data Cursor vemos las frecuencias que contribuyen más a la energía: f₁=0.0833 Hz, f₃=0.25 Hz, f₇=0.583 Hz y f₈=0.667 Hz. Estas dos últimas comparten la misma energía y posiblemente, la depositaria sea una única frecuencia intermedia entre las dos que no ha sido detectada por el análisis que hemos hecho basado en una frecuencia fundamental f₁=1/12 Hz y múltiplos enteros de dicha frecuencia.

....
figure
df=1/(N*dt);  %intervalo de frecuencias
fk=(1:N/2)*df;
energia=(a.^2+b.^2)/(2*df);
semilogy(fk,energia,'-ro','markersize',3,'markerfacecolor','r')
grid on
xlabel('Frecuencia (Hz)')
ylabel('Energía')
title('Espectro de energía')

Mejoramos el análisis incrementando el tiempo P en el que tomamos los datos manteniendo el intervalo Δt=0.375 s constante. Cuando se incrementa el valor de N hay más términos que contribuyen a la serie de Fourier, hay más armónicos. La frecuencia límite f_c=1/(2Δt) no cambia pero el intervalo Δf=1/T=1/(N·Δt) decrece, incremantándose la resolución en la frecuencia.

Supongamos que queremos diseñar un experimento en el esperamos que la frecuencia más alta sea f_c=1 Hz y queremos discriminar frecuencias separadas por Δf=0.005 Hz. Para ello, tendríamos que tomar muestras en intervalos de tiempo Δt tal que f_c=1/(2Δt)= 1 Hz, por lo que Δt=0.5 s. Durante un tiempo P tal que Δf=1/P=0.005 Hz, por lo que P=200 s, o P=N·Δt, por lo tanto N=400 datos.

Transformada Rápida de Fourier

Al hacer la transformada rápida de Fourier g=fft(x_k), obtenemos N=32 números complejos g_i de los cuales tomamos N/2. El espectro de energía viene dado por la fórmula.

${\displaystyle S(i)=\frac{2}{N^2}\frac{{\left|g_i\right|}^2}{\Delta f}i=\mathrm{1,2,3...}\frac{N}{2}}$

xk=[-0.01,-0.14,-0.09,0.47,1.3,1.89,2.16,2.34,2.37,1.93,1.09,
0.39,0.1,-0.03,-0.17,-0.15,0.15,0.32,-0.01,-0.67,-1.24,-1.68,
-2.18,-2.56,-2.39,-1.72,-1.03,-0.59,-0.2,0.2,0.31,0.0];
N=length(xk);
dt=0.375; %intervalo de tiempo
g=fft(xk);
df=1/(N*dt);  %intervalo de frecuencias
fk=(0:N/2)*df;
energia=2*abs(g).^2/(N^2*df);
semilogy(fk,energia(1:N/2+1),'-ro','markersize',3,'markerfacecolor','r')
grid on
xlabel('Frecuencia (Hz)')
ylabel('Energía')
title('Espectro de energía')

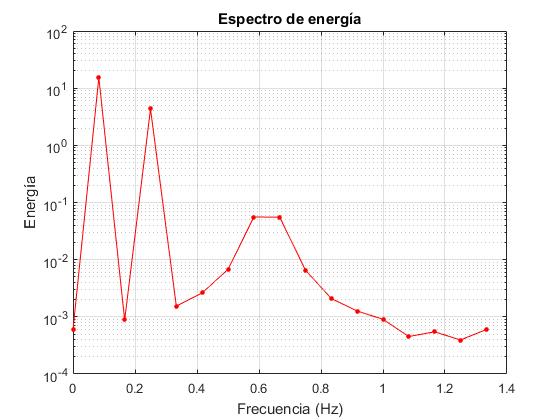
Obtenemos prácticamente el mismo resultado que con la transformada discreta de Fourier pero con mucho menos trabajo.

En las siguientes páginas, veremos ejemplos interesantes de aplicación de la Transformada Rápida de Fourier (FFT)

Coeficientes de la serie finita de Fourier

En este apartado, vamos a obtener los coeficientes a_k, b_k de la serie finita de Fourier de un modo análogo a la aproximación continua.

Supongamos que hemos tomado N datos (un número par) x(t_m) durante un intervalo de tiempo P en los instantes t_m=mP/N, m=1,2,3...N de una señal periódica de periodo P

Definimos la serie finita de Fourier del siguiente modo

${\displaystyle x(t)=a_0+{\displaystyle \sum _{k=1}^{N/2}{a}_k\cos \left(2\pi k\frac{t}{P}\right)}+{\displaystyle \sum _{k=1}^{N/2-1}{b}_k\sin \left(2\pi k\frac{t}{P}\right)}}$

Vamos a determinar las fórmulas que nos permiten calcular los coeficientes a_k, b_k. Para ello, partimos de la suma de N términos de una progresión geométrica

${\displaystyle \begin{array}{l}{\displaystyle \sum _{m=1}^N\exp \left(2\pi ik\frac{t_m}{P}\right)}={\displaystyle \sum _{m=1}^N\exp \left(2\pi ik\frac{m}{N}\right)}={\displaystyle \sum _{m=1}^N{r}^m}=\{\begin{array}{l}r\frac{1-r^N}{1-r}r\ne 1\\ Nr=1\end{array}\\ r=\exp \left(\frac{2\pi ik}{N}\right)\end{array}}$

Donde i es la unidad imaginaria, $\sqrt{-1}$. Como vemos r^N=1 (el numerador y por tanto, la suma de los términos de la serie son cero) cuando k es distinto de cero. Como exp(ix)=cos(x)+isin(x), igualando a cero, la parte real e imaginaria, obtenemos los siguientes resultados

${\displaystyle \begin{array}{l}{\displaystyle \sum _{m=1}^N\cos \left(2\pi k\frac{t_m}{P}\right)}={\displaystyle \sum _{m=1}^N\cos \left(2\pi k\frac{m}{N}\right)}=\{\begin{array}{l}0k\ne 0\\ Nk=\mathrm{0,}N\end{array}\\ {\displaystyle \sum _{m=1}^N\sin \left(2\pi k\frac{x_m}{P}\right)}=0\end{array}}$

>> format bank
>> N=12;
>> k=3;
>> sum(cos(2*pi*k*(1:N)/N))
ans =  0.00 
>> sum(sin(2*pi*k*(1:N)/N))
ans =   0.00
>> k=0;
>> sum(cos(2*pi*k*(1:N)/N))
ans =    12.00
>> sum(sin(2*pi*k*(1:N)/N))
ans =     0
>> k=N;
>> sum(cos(2*pi*k*(1:N)/N))
ans =    12
>> sum(sin(2*pi*k*(1:N)/N))
ans =  -0.00

De este resultado, se deducen estos otros que involucran los productos de senos y cosenos

${\displaystyle \begin{array}{l}{\displaystyle \sum _{m=1}^N\cos \left(2\pi k\frac{t_m}{P}\right)}\cos \left(2\pi j\frac{t_m}{P}\right)=\\ \frac{1}{2}{\displaystyle \sum _{m=1}^N\left(\cos \left(2\pi (k+j)\frac{t_m}{P}\right)+\cos \left(2\pi (k-j)\frac{t_m}{P}\right)\right)}=\{\begin{array}{l}0k\ne j\\ N/2k=j\ne \mathrm{0,}N/2\\ Nk=j=\mathrm{0,}N/2\end{array}\\ {\displaystyle \sum _{m=1}^N\cos \left(2\pi k\frac{t_m}{P}\right)}\sin \left(2\pi j\frac{t_m}{P}\right)=0\\ {\displaystyle \sum _{m=1}^N\sin \left(2\pi k\frac{t_m}{P}\right)}\sin \left(2\pi j\frac{t_m}{P}\right)=\\ \frac{1}{2}{\displaystyle \sum _{m=1}^N\left(\cos \left(2\pi (k-j)\frac{t_m}{P}\right)-\cos \left(2\pi (k+j)\frac{t_m}{P}\right)\right)}=\{\begin{array}{l}0k\ne j\\ N/2k=j\ne \mathrm{0,}N/2\\ 0k=j=\mathrm{0,}N/2\end{array}\end{array}}$

>> format bank
>> N=12;
>> k=3; j=5;
>> sum(cos(2*pi*k*(1:N)/N).*cos(2*pi*j*(1:N)/N))
ans =   0.0
>> sum(sin(2*pi*k*(1:N)/N).*sin(2*pi*j*(1:N)/N))
ans =   0.00
>> sum(sin(2*pi*k*(1:N)/N).*cos(2*pi*j*(1:N)/N))
ans =  -0.00
>> k=5;j=5;
>> sum(cos(2*pi*k*(1:N)/N).*cos(2*pi*j*(1:N)/N))
ans =    6.00
>> sum(cos(2*pi*k*(1:N)/N).*sin(2*pi*j*(1:N)/N))
ans =  -0.00
>> sum(sin(2*pi*k*(1:N)/N).*sin(2*pi*j*(1:N)/N))
ans =    6.00
>> k=0;j=0;
>> sum(cos(2*pi*k*(1:N)/N).*cos(2*pi*j*(1:N)/N))
ans =    12.00
>> sum(cos(2*pi*k*(1:N)/N).*sin(2*pi*j*(1:N)/N))
ans =     0
>> sum(sin(2*pi*k*(1:N)/N).*sin(2*pi*j*(1:N)/N))
ans =     0
>> k=N/2;j=N/2;
>> sum(cos(2*pi*k*(1:N)/N).*cos(2*pi*j*(1:N)/N))
ans =    12.00
>> sum(cos(2*pi*k*(1:N)/N).*sin(2*pi*j*(1:N)/N))
ans =  -0.00
>> sum(sin(2*pi*k*(1:N)/N).*sin(2*pi*j*(1:N)/N))
ans =   0.00

Para calcular los coeficientes a_j multiplicamos la serie finita x(t) por cos(2πj·t/P) y sumamos para los N datos

${\displaystyle \begin{array}{l}{\displaystyle \sum _{m=1}^{N}x(t_m)\cos }\left(2\pi j\frac{t_m}{P}\right)=a_0{\displaystyle \sum _{m=1}^N\cos }\left(2\pi j\frac{t_m}{P}\right)+{\displaystyle \sum _{m=1}^N\left({\displaystyle \sum _{k=1}^{N/2}{a}_k\cos \left(2\pi k\frac{t_m}{P}\right)}\right)}\cos \left(2\pi j\frac{t_m}{P}\right)+\\ +{\displaystyle \sum _{m=1}^N\left({\displaystyle \sum _{k=1}^{N/2-1}{b}_k\sin \left(2\pi k\frac{t_m}{P}\right)}\right)}\cos \left(2\pi j\frac{t_m}{P}\right)\end{array}}$

Para j=0, obtenemos a₀

${\displaystyle a_0=\frac{1}{N}{\displaystyle \sum _{m=1}^{N}x(t_m)}}$

Para j≠0, N/2, obtenemos a_j, j=1,2,...N/2-1

${\displaystyle a_j=\frac{2}{N}{\displaystyle \sum _{m=1}^{N}x(t_m)\cos }\left(2\pi j\frac{t_m}{P}\right)j=\mathrm{1,2,...}\frac{N}{2}-1}$

Para j=N/2, obtenemos a_N/2,

${\displaystyle a_{N/2}=\frac{1}{N}{\displaystyle \sum _{m=1}^{N}x(t_m)\cos }\left(m\pi \right)}$

Para calcular los coeficientes b_j multiplicamos la serie finita x(t) por sin(2πj·t/P) y sumamos para los N datos

${\displaystyle \begin{array}{l}{\displaystyle \sum _{m=1}^{N}x(t_m)\sin }\left(2\pi j\frac{t_m}{P}\right)=a_0{\displaystyle \sum _{m=1}^N\sin }\left(2\pi j\frac{t_m}{P}\right)+{\displaystyle \sum _{m=1}^N\left({\displaystyle \sum _{k=1}^{N/2}{a}_k\cos \left(2\pi k\frac{t_m}{P}\right)}\right)}\sin \left(2\pi j\frac{t_m}{P}\right)+\\ +{\displaystyle \sum _{m=1}^N\left({\displaystyle \sum _{k=1}^{N/2-1}{b}_k\sin \left(2\pi k\frac{t_m}{P}\right)}\right)}\sin \left(2\pi j\frac{t_m}{P}\right)\end{array}}$

Obtenemos b_j, j=1,2,...N/2-1

${\displaystyle b_j=\frac{2}{N}{\displaystyle \sum _{m=1}^{N}x(t_m)\sin }\left(2\pi j\frac{t_m}{P}\right)j=\mathrm{1,2,3...}\frac{N}{2}-1}$

Bibliografía

Dos primeros apartados

Whitford D., Vieira M. Waters J. Teaching time-series analysis. I. Finite Fourier analysis of ocean waves. Am. J. Phys. 69 (4), April 2001, pp. 490-496.