Análisis de Fourier de los desplazamiento de las olas

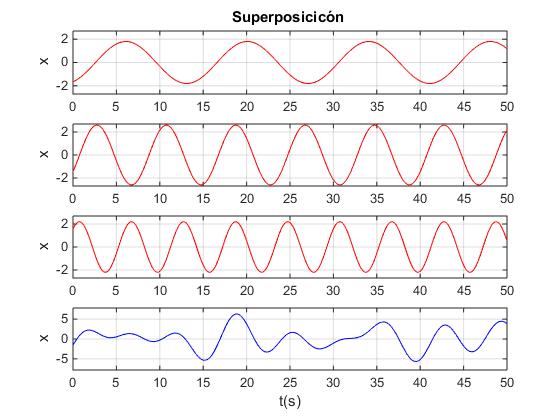
En la figura, se muestra una onda irregular (en color azul) obtenida a partir de la superposición de ondas con amplitudes 1.8, 2.6 y 2.2 y periodos 14, 8 y 6 respectivamente. Las fases iniciales son números aleatorios en el intervalo 0 a 2π.

subplot(4,1,1)
t=0:0.1:50;
x1=1.8*sin(2*pi*t/14+2*pi*rand);
plot(t,x1,'r')
ylabel('x')
title('Superposicicón ')
ylim([-2.7,2.7])
grid on

subplot(4,1,2)
x2=2.6*sin(2*pi*t/8+2*pi*rand);
plot(t,x2,'r')
ylabel('x')
ylim([-2.7,2.7])
grid on

subplot(4,1,3)
x3=2.2*sin(2*pi*t/6+2*pi*rand);
plot(t,x3,'r')
ylabel('x')
ylim([-2.7,2.7])
grid on

subplot(4,1,4)
x=x1+x2+x3;
plot(t,x,'b')
xlabel('t(s)')
ylabel('x')
ylim([-7.8,7.8])
grid on

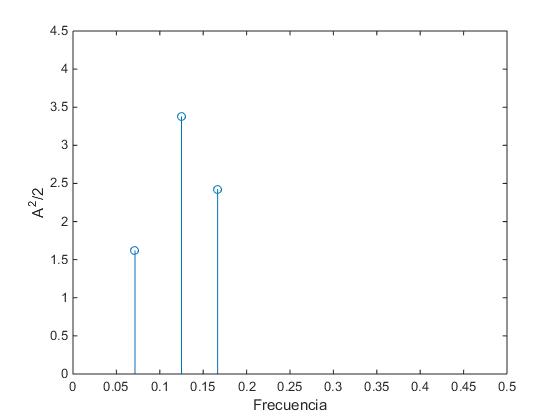
La contribución de cada componente a la superposición se muestra en otro diagrama. En el eje horizontal se ponen las frecuencias f_i y en el eje vertical el cuadrado de las amplitudes dividido entre dos. $\frac{1}{2} a_{i}^{2}$ . En el análisis de las olas por su carácter aleatorio, las fases iniciales carecen de relevancia.

figure
T=[14,8,6]; %Periodos
A=[1.8,2.6,2.2]; %amplitudes
stem(1./T,A.^2/2)
axis([0,0.5,0,4.5])
xlabel('Frecuencia')
ylabel('A^2/2')

La densidad espectral S(f) se define

$S (f) = \frac{1}{2} \frac{a^{2}}{Δ f}$

Donde Δf es el intervalo de frecuencias

Multiplicando por la aceleración de la gravedad g y por la densidad del agua ρ tenemos un espectro de energías, que nos da la contribución de cada componente de frecuencia, a la energía de las olas.

Transformada Rápida de Fourier

El fichero olasZ.txt contiene N=2304 datos de la elevación z del agua tomados durante T₀=30 minutos. El intervalo de tiempo entre dos medidas consecutivas Δt=1/f_s, donde f_s=1.28 Hz es la frecuencia de muestreo.

La Transformada Rápida de Fourier nos proporciona N números complejos a₀+i·b₀, a₁+i·b₁....a_N-1+i·b_N-1.que corresponden a las frecuencias f_j=j/T₀ con j=0,1,2,...N-1.

El intervalo de frecuencias es Δf=1/T₀ y la densidad espectral

$S (j) = \frac{2}{N^{2}} \frac{(a_{j}^{2} + b_{j}^{2})}{Δ f}$

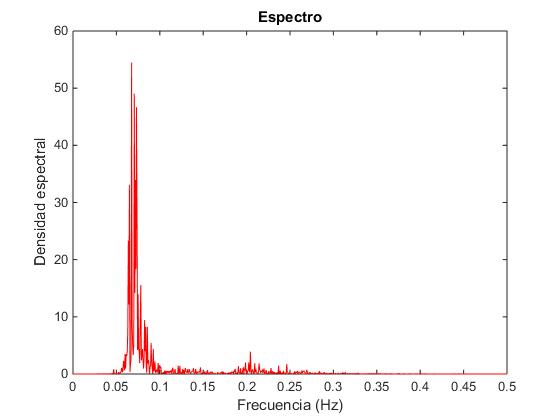
El desplazamiento z dado en cm lo convertimos en metros, dividiendo entre 100, y tomamos los primeros N=2048 (potencia de 2) datos de los 2304 disponibles, para hacer la transformada FFT.

load olasZ.txt;
z=olasZ-mean(olasZ);
Fs=1.28;
clear olasZ
N=2048;
df=Fs/N;  %intervalo de frecuencias
g=fft(z(1:N)/100);  %el desplazamiento en metros
g=2*abs(g).^2/(N^2*df);
g=g(1:N/2);      %Toma solamente N/2 datos
frec=(0:N/2-1)*df;   %Frecuencias
plot(frec,g,'r')
xlim([0,0.5])
xlabel('Frecuencia (Hz)')
ylabel('Densidad espectral')
title('Espectro')

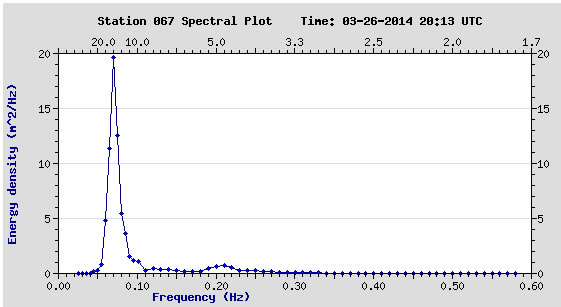
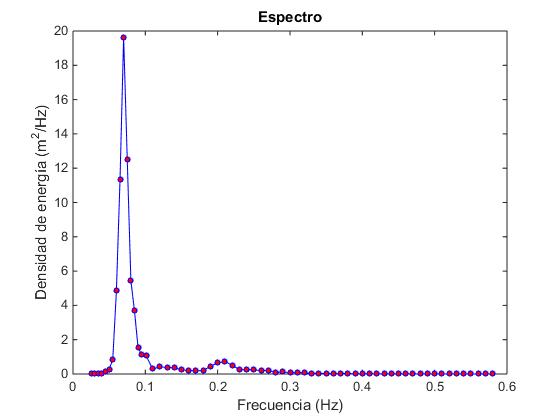
La web CDIP "The Coastal Data Information Program" dispone también de datos de frecuencias, cuya representación gráfica es la siguiente

Se proporciona también un fichero de datos, cuya cabecera y primeras filas de datos es la siguiente:

  File Name: sp06701201403262013     Analyzed(UTC): 2014 03/26 2043 hrs
  Station Name: SAN NICOLAS ISLAND, CA                            
  Location: 33 13.24 N 119 52.88 W   Sensor Type: Waverider Drctnl Buoy    
  Water Depth(m):   335 MLLW    Sensor Depth(m): N/A      Sensor Elev(m):  335.3
  Shore Normal(deg): N/A        Source File: is06701201403262040
  Sample Length(s):  1600       Sample Rate(Hz): 1.280
  Hs(m):  2.47   Tp(s): 14.29   Dp(deg): 289   Ta(s): 10.53

   freq   Band      energy   Dmean     a1       b1       a2       b2    Check
    Hz    width     m*m/Hz    deg                                       factor
  0.0250  0.0050     0.0033   289    0.0722  -0.2092  -0.3818  -0.5768   2.55
  0.0300  0.0050     0.0081    11    0.0246   0.0046  -0.4763  -0.4087   2.55
  0.0350  0.0050     0.0247   157   -0.1158   0.0495  -0.2118  -0.5615   2.55

Para reproducir la figura anterior solamente precisamos de la primera y tercera columna.

Seleccionamos los datos con el puntero del ratón en la página web, los copiamos y los pegamos en un documento nuevo de Microsoft Word. Eliminamos la cabecera del fichero, dejando solamente las columnas de datos. Manteniendo pulsada la tecla Alt, con el ratón seleccionamos la segunda columna y la eliminamos (cortar). Seleccionamos las columnas a la derecha de la columna energy y las eliminamos, quedando solamente dos columnas tituladas freq Hz y energy m*m/Hz. Guadamos el texto sin formato en una carpeta accesible a MATLAB con el nombre olasZ_e.txt que se descarga en este enlace

Importamos el fichero de datos olasZ_e.txt seleccionando en el menú File/Import Data, en Output Type seleccionamos Column vectors. Obtenemos dos vectores, que renombramos como f (frecuencias) e (energías) en la ventana Workspace.

>> plot(f,e,'-bo','markersize',4,'markerfacecolor','r')
>> xlabel('Frecuencia (Hz)')
>> ylabel('Densidad de energía (m^2/Hz)')
>> title('Espectro')
>> xlim([0,0.6])

Bibliografía

Whitford D., Waters J., Vieira M. Teaching time-series analysis. II. Wave height and water surface elevation probability distributions. Am. J. Phys. 69 (4), April 2001, pp. 497-504.

Direcciones de Internet que podrían ser de interés para el lector

Mace Toolbox

MACE is a MATLAB toolbox collects MATLAB .m functions for coastal engineers and researchers.

Processing of wave data from pressure sensors

OCEANLYZ, Ocean Wave Analyzing Toolbox