La forma funcional de la distribución de Rayleigh es

${\displaystyle f(x)=\frac{2x}{b^2}\exp \left(-\frac{x^2}{b^2}\right)x\ge 0}$

La función f(x) representa la probabilidad de que la velocidad del viento x esté en un intervalo entre x y x+dx. El área bajo f(x) es la unidad.

${\displaystyle {\displaystyle {\int }_0^{\infty }f(x)·dx=1}}$

como puede comprobarse fácilmente. La función de distribución de Rayleigh es un caso particular de la de Weibull para k=2.

El valor medio de la velocidad <x>

${\displaystyle <x>={\displaystyle {\int }_0^{\infty }x·f(x)·dx=\frac{\sqrt{\pi }}{2}}b}$

Para calcular el valor medio utilizamos el siguiente resultado tomado de una tabla de integrales

${\displaystyle {\displaystyle {\int }_0^{\infty }{x}^2\exp (-\alpha x^2)dx}=\frac{1}{4}\sqrt{\frac{\pi }{{\alpha }^3}}}$

No hay que realizar un ajuste de datos a la función de Rayleigh, basta conocer la velocidad media del sitio <x> que está directamente relacionada con el parámetro b.

La función de distribución de Rayleigh se expresa en términos del valor medio <x> de la velocidad

${\displaystyle f(x)=\frac{\pi x}{2<x{>}^2}\exp \left(-\frac{\pi }{4}{\left(\frac{x}{<x>}\right)}^2\right)x\ge 0}$

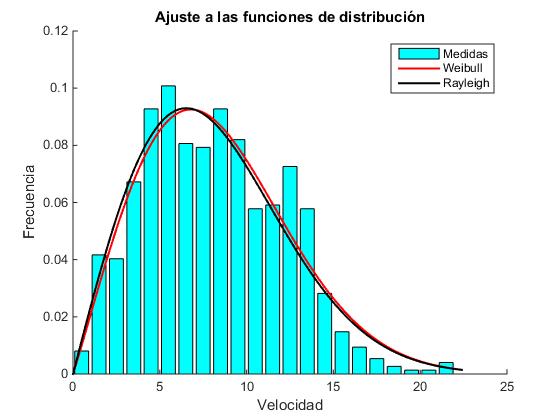
En la figura, se representa la función de distribución de Rayleigh para varios valores de la velocidad media del viento.

media=[4 6 8 10];
g=@(med,x) pi*x.*exp(-pi*x.^2/(4*med^2))/(2*med^2);
x=linspace(0,25,100);
hold on
for i=1:length(media)
     plot(x,g(media(i),x),'displayName',num2str(media(i)))
end
ylim([0 0.25])
xlabel('x')
ylabel('f(x)')
title('Función de Rayleigh')
legend('-DynamicLegend','location','NorthEast')
hold off

La velocidad para la cual la función de distribución de Rayleigh alcanza un máximo se obtiene derivando f(x) e igualando a cero.

${\displaystyle x_{\max }=\sqrt{\frac{2}{\pi }}<x>}$

Tomando una velocidad media <x>=6 m/s, el máximo de la curva de color azul se produce para x_max=4.79 y su valor es 0.1267.

La desviación estándar σ

${\displaystyle {\sigma }^2=\left(\frac{4}{\pi }-1\right)<x{>}^2}$

En la página anterior, calculamos la media y la desviación estándar de las medidas de la velocidad del viento a lo largo del mes de Marzo, comparamos estos resultados con la desviación estándar dada por la función de distribución de Rayleigh

%medidas de las velocidades del viento
>> media=sum(velocidad)/length(velocidad)
media =     8.1741
>> estandar=std(velocidad)
estandar =    3.9761
%función de distribución de Rayleigh
>> estandar=sqrt(4/pi-1)*media
estandar =    4.2728

La probabilidad acumulada F(x) vale

${\displaystyle F(x)=1-\exp \left(-\frac{\pi }{4}{\left(\frac{x}{<x>}\right)}^2\right)}$

La probabilidad de que la velocidad del viento x este en el intervalo comprendido entre x₀ y x₁.

${\displaystyle P(x_0\le x<x_1)={\displaystyle {\int }_{x_0}^{x_1}f(x)·dx=\exp \left(-\frac{\pi }{4}{\left(\frac{x_0}{<x>}\right)}^2\right)}-\exp \left(-\frac{\pi }{4}{\left(\frac{x_1}{<x>}\right)}^2\right)}$

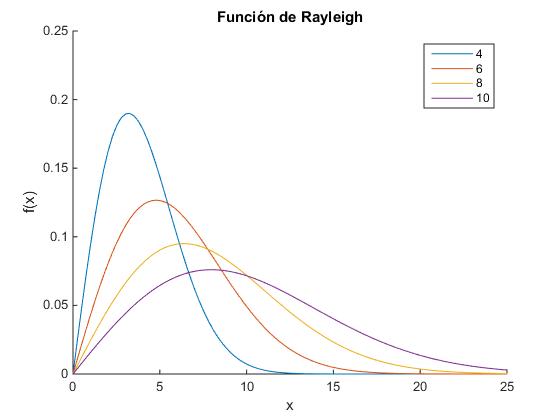
Representamos f(x) y calculamos la probabilidad P(x) en el intervalo (4.5, 5.5), es decir, centrado en x₀=5 y de anchura 1.0.

med=6; %valor medio de las velocidades del viento
f=@(x) pi*x.*exp(-pi*x.^2/(4*med^2))/(2*med^2);
x=linspace(0,20,100);
y=f(x);
hold on
plot(x,y,'b')
x0=4.5; x1=5.5;
xx=[x0 x0 x(x>x0 & x<x1) x1 x1];
yy=[0 f(x0) y(x>x0 & x<x1) f(x1) 0];
fill(xx,yy,'y');
res=quad(f,x0,x1)
prob=exp(-pi*x0^2/(4*med^2))-exp(-pi*x0^2/(4*med^2));
text(x1+2, max(y),num2str(res));
title('Probabilidad')
xlabel('x')
ylabel('f(x)')
hold off

Obtenemos el mismo resultado efectuando la integración numérica de la función de Rayleigh f(x) mediante la función quad, que a partir de la expresión de la probabilidad P(x₀≤x<x₁) deducida anteriormente.

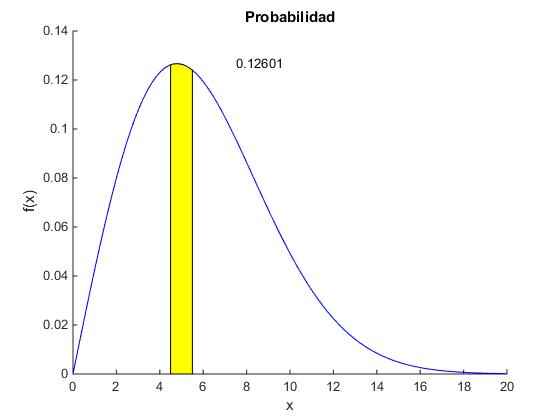
Comparación de Weibull y Rayleigh

clear,clc
velocidad=xlsread('WhiteDeer2013','Mar','F2:F745');
%interpolar si es necesario
if any(isnan(velocidad)) %si hay algún NaN
    x=1:length(velocidad);
    i=find(~isnan(velocidad));
    velocidad=interp1(x(i),velocidad(i),x);
end
%histograma
x=0.5:1:max(velocidad);
horas=hist(velocidad,x);
%convierte a frecuencias y ajusta a la función de Weibull
frec=horas/sum(horas);
f=@(a,x) (a(1)/a(2))*((x/a(2)).^(a(1)-1)).*exp(-(x/a(2)).^a(1));
a0=[2 8];  %valor inicial de los parámetros
af=nlinfit(x,frec,f,a0);
hold on 

%diagrama de barras
bar(x,frec,'c');
%representa la curva da juste
x=linspace(0,max(velocidad),100);
%función de Weibull
y=f(af,x);
plot(x,y,'r','Linewidth',1.5)

%función de Rayleigh
media=sum(velocidad)/length(velocidad);
g=@(x) pi*x.*exp(-pi*x.^2/(4*media^2))/(2*media^2);
y=g(x);
plot(x,y,'k','Linewidth',1.5)
title('Ajuste a las funciones de distribución')
xlabel('Velocidad')
ylabel('Frecuencia')
legend('Medidas','Weibull','Rayleigh')
hold off