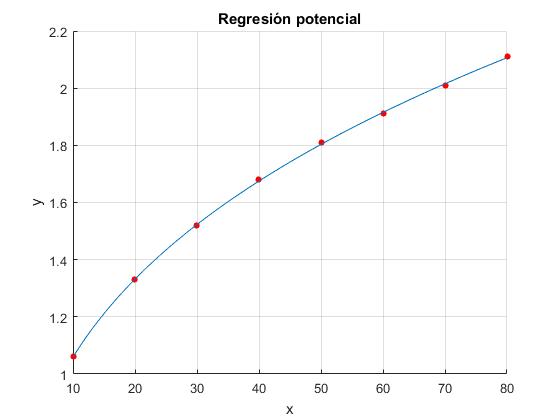
Ajuste de datos. Regresión

Regresión lineal

Abordaremos en esta página las distribuciones bidimensionales. Las observaciones se dispondrán en dos columnas, de modo que en cada fila figuren la abscisa x y su correspondiente ordenada y. La importancia de las distribuciones bidimensionales radica en investigar como influye una variable sobre la otra. Esta puede ser una dependencia causa efecto, por ejemplo, la cantidad de lluvia (causa), da lugar a un aumento de la producción agrícola (efecto). O bien, el aumento del precio de un bien, da lugar a una disminución de la cantidad demandada del mismo.

Si utilizamos un sistema de coordenadas cartesianas para representar la distribución bidimensional, obtendremos un conjunto de puntos conocido con el diagrama de dispersión, cuyo análisis permite estudiar cualitativamente, la relación entre ambas variables. El siguiente paso, es la determinación de la dependencia funcional entre las dos variables x e y que mejor ajusta a la distribución bidimensional. Se denomina regresión lineal cuando la función es lineal, es decir, requiere la determinación de dos parámetros: la pendiente y la ordenada en el origen de la recta de regresión, y=ax+b.

La regresión nos permite además, determinar el grado de dependencia de las series de valores X e Y, prediciendo el valor y estimado que se obtendría para un valor x que no esté en la distribución.

Vamos a determinar la ecuación de la recta que mejor ajusta a los datos representados en la figura. Se denomina error ε_i a la diferencia y_i-y, entre el valor observado y_i, y el valor ajustado y= ax_i+b, tal como se ve en la figura inferior. El criterio de ajuste se toma como aquél en el que la desviación cuadrática media sea mínima, es decir, debe de ser mínima la suma

$E = \sum_{1}^{n} ε_{i}^{2} = \sum_{1}^{n} {(y_{i} - (a x_{i} + b))}^{2}$

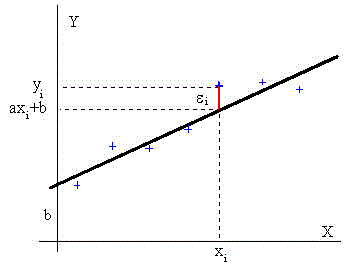
El extremos de una función: máximo o mínimo se obtiene cuando las derivadas de E respecto de a y de b sean nulas. Lo que da lugar a un sistema de dos ecuaciones con dos incógnitas del que se despeja a y b.

$\begin{array}{l} \frac{\partial E}{\partial a} = 0 \frac{\partial E}{\partial b} = 0 \\ a = \frac{n \sum_{1}^{n} x_{i} y_{i} - (\sum_{1}^{n} x_{i}) (\sum_{1}^{n} y_{i})}{n \sum_{1}^{n} x_{i}^{2} - {(\sum_{1}^{n} x_{i})}^{2}} b = \frac{\sum_{1}^{n} y_{i} - a \sum_{1}^{n} x_{i}}{n} \end{array}$

Expresiones más elaboradas nos permiten determinar el error de a, Δa y el error de b, Δb

$\begin{array}{l} Δ a = \frac{\sqrt{n} \cdot σ}{\sqrt{n \sum_{1}^{n} x_{i}^{2} - {(\sum_{1}^{n} x_{i})}^{2}}} σ = \sqrt{\frac{\sum_{1}^{n} {(y_{i} - a x_{i} - b)}^{2}}{n - 2}} \\ Δ b = Δ a \cdot \sqrt{\frac{\sum_{1}^{n} x_{i}^{2}}{n}} \end{array}$

La pendiente de la recta se escribirá a±Δa, y la ordenada en el origen b±Δb. Véase las reglas para expresar una medida y su error de una magnitud.

El coeficiente de correlación es otro parámetro para el estudio de una distribución bidimensional, que nos indica el grado de dependencia entre las variables X e Y. El coeficiente de correlación r es un número que se obtiene mediante la fórmula.

$r = \frac{\sum_{1}^{n} (x_{i} - < x >) (y_{i} - < y >)}{\sqrt{\sum_{1}^{n} {(x_{i} - < x >)}^{2}} \sqrt{\sum_{1}^{n} {(y_{i} - < y >)}^{2}}}$

El numerador es el producto de las desviaciones de los valores X e Y respecto de sus valores medios. En el denominador tenemos las desviaciones cuadráticas medias de X y de Y.

El coeficiente de correlación puede valer cualquier número comprendido entre -1 y +1.

Cuando r=1, la correlación lineal es perfecta, directa.
Cuando r=-1, la correlación lineal es perfecta, inversa
Cuando r=0, no existe correlación alguna, independencia total de los valores X e Y

Ejemplo

Un vehículo que se mueve supuestamente con velocidad constante. Los datos de las medidas del tiempo en cuatro posiciones separadas 900 m son las siguientes

Tiempo t (s)	Posición x (m)
17.6	0
40.4	900
67.7	1800
90.1	2700

Ajustar los datos a la línea recta

x=x₀+vt

y estimar el mejor valor de la velocidad v aplicando el procedimiento de mínimos cuadrados

function [a b]=regresion(x,y)
    n=length(x);
    a=zeros(2,1);
    b=zeros(2,1);
    
    %pendiente de la recta de regresión, a
    a(1)=(n*sum(x.*y)-sum(x)*sum(y))/(n*sum(x.^2)-sum(x)*sum(x));
    %ordenada en el origen, b
    b(1)=(sum(y)-a(1)*sum(x))/n;
   
    % errores de a y de b
    sd2=sum((y-a(1)*x-b(1)).^2);
    a(2)=sqrt(sd2/(n-2))/sqrt(sum(x.^2)-sum(x)*sum(x)/n);
    b(2)=sqrt(sum(x.^2)/n)*a(2);
end

En el vector a de dimensión 2 hemos guardado la pendiente en a(1) y su error en a(2)
En el vector b de dimensión 2 hemos guardado la ordenada en b(1) y su error en b(2)

Escribimos un script para calcular la pendiente a de la recta de regresión, su error Δa, la ordenada en el origen b y su error Δb.

t=[17.6 40.4 67.7 90.1];
x=[0 900 1800 2700];
[a b]=regresion(t,x);
fprintf('pendiente a= %2.3f, error %1.3f\n',a(1),a(2));
fprintf('ordenada b= %3.3f, error %3.3f\n',b(1),b(2));

%gráfica
plot(t,x,'ro','markersize',8,'markerfacecolor','r')
tmin=min(t);
xmin=a(1)*tmin+b(1);
tmax=max(t);
xmax=a(1)*tmax+b(1);
line([tmin tmax],[xmin xmax]); %recta
xlabel('t')
ylabel('x')
grid on
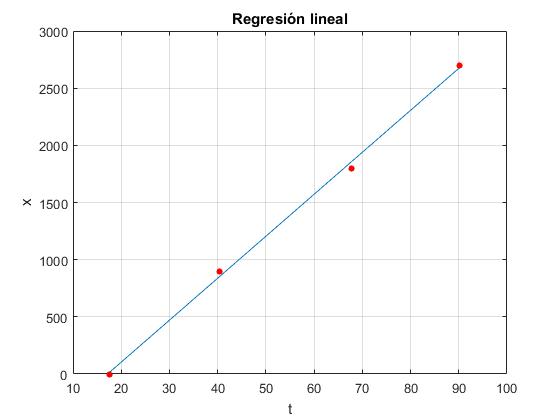
title('Regresión lineal')

En la ventana de comandos corremos el script

pendiente a= 36.710, error 1.001
ordenada b= -630.509, error 60.580

Queda como trabajo al lector calcular el coeficiente de correlación. Solución r=0.99926

Ajuste no lineal, que se transforma en regresión lineal

Estudiamos algunos ejemplos de ajuste a funciones no lineales, que se pueden transformar en ajuste a una función lineal, mediante un cambio de variable

La función potencial

y=b·x^a

Se puede trasformar en

log(y)=a·log(x)+log(b)

Si usamos las nuevas variables X=log(x) e Y=log(y), obtenemos la relación lineal

Y=AX+B.

Donde B=log(b)

Ejemplo:

x	10	20	30	40	50	60	70	80
y	1.06	1.33	1.52	1.68	1.81	1.91	2.01	2.11

Representamos estos datos en un diagrama doblemente logarítmico mediante el comando loglog

x=[10 20 30 40 50 60 70 80];
y=[1.06 1.33 1.52 1.68 1.81 1.91 2.01 2.11];
loglog(x,y,'ro','markersize',4,'markerfacecolor','r')
xlabel('x')
ylabel('y')
grid on
title('Función potencial')

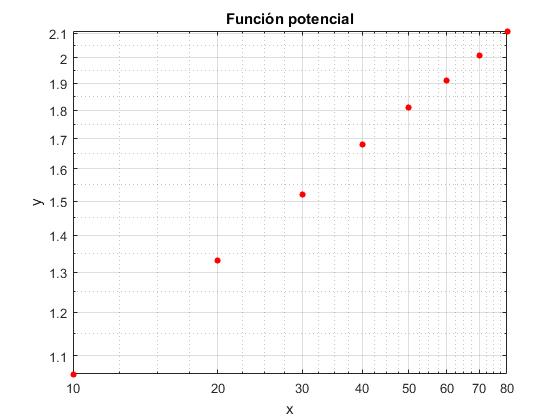
Para determinar la recta de regresión, se transforma esta tabla de datos en esta otra

X=log(x)	1.0	1.30	1.477	1.60	1.699	1.778	1.845	1.903
Y=log(y)	0.025	0.124	0.182	0.225	0.258	0.281	0.303	0.324

Calculamos mediante la función regresion los parámetros A y B.

x=[10 20 30 40 50 60 70 80];
y=[1.06 1.33 1.52 1.68 1.81 1.91 2.01 2.11];
[A,B]=regresion(log10(x),log10(y));
fprintf('exponente a= %2.3f\n',A(1));
fprintf('coeficiente b= %3.3f\n',10^B(1));

%gráfica
hold on
plot(x,y,'ro','markersize',4,'markerfacecolor','r')
z=@(x) (10^B(1))*x.^A(1);
fplot(z,[x(1),x(end)])
grid on
xlabel('x')
ylabel('y')
title('Regresión potencial')
hold off

Corremos el script en la ventana de comandos

exponente a= 0.331
coeficiente b = 0.495

Función exponencial

y=b·e^ax

Tomando logaritmos neperianos en los dos miembros resulta

ln y=ax+ln(b)

Si ponemos ahora X=x, e Y=ln(y), obtenemos la relación lineal

Y=AX+B

Donde B=ln(b).

Ejemplo:

x	12	41	93	147	204	264	373	509	773
y	930	815	632	487	370	265	147	76	17

Representamos estos datos en un diagrama semilogarítmico mediante el comando semilogy

x=[12 41 93 147 204 264 373 509 773];
y=[930 815 632 487 370 265 147 76 17];
semilogy(x,y,'ro','markersize',4,'markerfacecolor','r')
xlabel('x')
ylabel('y')
title('Función exponencial')
grid on

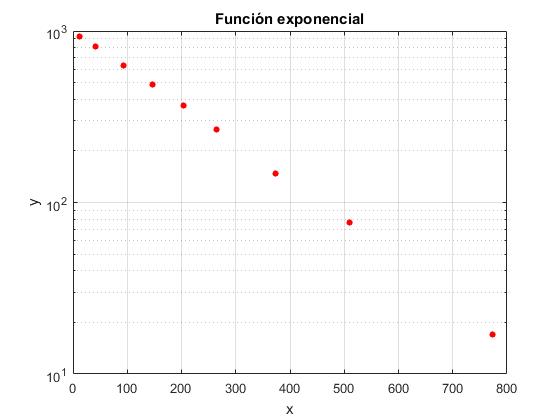
Para determinar la recta de regresión, se transforma esta tabla de datos en esta otra

X=x	12	41	93	147	204	264	373	509	773
Y=ln(y)	6.835	6.703	6.449	6.188	5.913	5.580	4.990	4.330	2.833

x=[12 41 93 147 204 264 373 509 773];
y=[930 815 632 487 370 265 147 76 17];
[A,B]=regresion(x,log(y));
fprintf('exponente a= %2.3f\n',A(1));
fprintf('coeficiente b = %3.3f\n',exp(B(1)));

hold on
plot(x,y,'ro','markersize',4,'markerfacecolor','r')
z=@(x) exp(B(1))*exp(x*A(1));
fplot(z,[x(1),x(end)])
xlabel('x')
ylabel('y')
grid on
title('Regresión exponencial')
hold off

Corremos el script en la ventana de comandos

exponente a= -0.005
coeficiente b = 1036.896

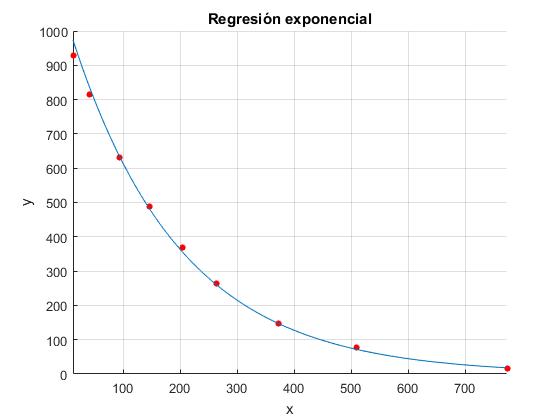
Otros ajustes a funciones no lineales que se transforman en una función lineal

En la tabla, se proporciona una lista de funciones no lineales que se pueden transformar en la función lineal Y=AX+B mediante un cambio de variable. Haciendo la sustitución obtenemos mediante el procedimiento de regresión lineal los parámetros A y B y a partir de ellos, los parámetros a y b de la función no lineal

Función no lineal	Sustitución	Parámetros A y B
y=a/x+b	X=1/x, Y=y	A=a, B=b
y=b/(x+a)	Y=1/y, X=x	A=1/b, B=a/b
y=c-b·exp(-ax)	Y=ln(c-y), X=x	A=-a, B=lnb
y=a·b^x	Y=ln(y), X=x	A=lnb, B=lna
y=ax·exp(bx)	Y=ln(c/x), X=x	A=b, B=lna
y=c/(1+b·exp(ax))	Y=ln(c/y-1), X=x	A=a, B=lnb
y=a·lnx+b	Y=y, X=lnx	A=a, B=b

Polinomio aproximador

Supongamos que hemos medido un conjunto de pares de datos (x_i, y_i) en una experiencia, por ejemplo, la posición de un móvil en ciertos instantes de tiempo.

Queremos obtener una función y=f(x) que se ajuste lo mejor posible a los valores experimentales. Se pueden ensayar muchas funciones, rectas, polinomios, funciones potenciales o logarítmicas.

Una vez establecido la función a ajustar se determinan sus parámetros, en el caso de un polinomio, serán los coeficientes del polinomio de modo que los datos experimentales se desvíen lo menos posible de la fórmula empírica. La función más sencilla es la función lineal y=ax+b, que hemos descrito en la sección anterior

Queremos aproximar un polinomio de grado n, a un conjunto de m pares de datos (x_j, y_j) de modo que n<m. Sea el polinomio

P(x)=a₁xⁿ+a₂x^n-1+...a_nx+a_n₊₁

Se calcula la cantidad

$S = \sum_{j = 1}^{m} {(P (x_{j}) - y_{j})}^{2} = \sum_{j = 1}^{m} {(a_{1} x_{j}^{n} + a_{2} x_{j}^{n - 1} + a_{n} x_{j} + a_{n + 1} - y_{j})}^{2}$

Para obtener los valores de los coeficientes del polinomio aproximador se tienen que determinar los valores de los coeficientes a₁, a₂, a₃, ...a_n, a_n+1 de forma que la cantidad S tome un valor mínimo.

Hagamos las derivadas parciales de S respecto de a₁, a₂, a₃, ...a_n, a_n+1 iguales a cero

$\begin{array}{l} \frac{1}{2} \frac{\partial S}{\partial a_{1}} = \sum_{j = 1}^{m} (a_{1} x_{j}^{n} + a_{2} x_{j}^{n - 1} + a_{n} x_{j} + a_{n + 1} - y_{j}) x_{j}^{n} \\ \frac{1}{2} \frac{\partial S}{\partial a_{2}} = \sum_{j = 1}^{m} (a_{1} x_{j}^{n} + a_{2} x_{j}^{n - 1} + a_{n} x_{j} + a_{n + 1} - y_{j}) x_{j}^{n - 1} \\ .................................... \\ \frac{1}{2} \frac{\partial S}{\partial a_{n}} = \sum_{j = 1}^{m} (a_{1} x_{j}^{n} + a_{2} x_{j}^{n - 1} + a_{n} x_{j} + a_{n + 1} - y_{j}) x_{j} \\ \frac{1}{2} \frac{\partial S}{\partial a_{n+1}} = \sum_{j = 1}^{m} (a_{1} x_{j}^{n} + a_{2} x_{j}^{n - 1} + a_{n} x_{j} + a_{n + 1} - y_{j}) \end{array}$

Obtenemos un sistema de n+1 ecuaciones con n+1 incógnitas, a₁, a₂, a₃, ...a_n, a_n+1

$\begin{array}{l} (\sum_{j = 1}^{m} x_{j}^{2 n}) a_{1} + (\sum_{j = 1}^{m} x_{j}^{2 n - 1}) a_{2} + ... + (\sum_{j = 1}^{m} x_{j}^{n + 1}) a_{n} + (\sum_{j = 1}^{m} x_{j}^{n}) a_{n + 1} = \sum_{j = 1}^{m} y_{j} x_{j}^{n} \\ (\sum_{j = 1}^{m} x_{j}^{2 n - 1}) a_{1} + (\sum_{j = 1}^{m} x_{j}^{2 n - 2}) a_{2} + ... + (\sum_{j = 1}^{m} x_{j}^{n}) a_{n} + (\sum_{j = 1}^{m} x_{j}^{n - 1}) a_{n + 1} = \sum_{j = 1}^{m} y_{j} x_{j}^{n - 1} \\ ......... \\ (\sum_{j = 1}^{m} x_{j}^{n}) a_{1} + (\sum_{j = 1}^{m} x_{j}^{n - 1}) a_{2} + ... + (\sum_{j = 1}^{m} x_{j}) a_{n} + m a_{n + 1} = \sum_{j = 1}^{m} y_{j} \end{array}$

Escribimos el sistema de ecuaciones, en forma matricial

$\begin{array}{l} (\begin{matrix} x_{1}^{n} & x_{2}^{n} & x_{3}^{n} & ... & x_{m}^{n} \\ x_{1}^{n - 1} & x_{2}^{n - 1} & x_{3}^{n - 1} & ... & x_{m}^{n - 1} \\ x_{1}^{n - 2} & x_{2}^{n - 2} & x_{3}^{n - 2} & ... & x_{m}^{n - 2} \\ ... & ... & ... & ... & ... \\ 1 & 1 & 1 & ... & 1 \end{matrix}) (\begin{matrix} x_{1}^{n} & ... & x_{1}^{2} & x_{1} & 1 \\ x_{2}^{n} & ... & x_{2}^{2} & x_{2} & 1 \\ x_{3}^{n} & ... & x_{3}^{2} & x_{3} & 1 \\ ... & ... & ... & ... & ... \\ x_{m}^{n} & ... & x_{m}^{2} & x_{m} & 1 \end{matrix}) (\begin{matrix} a_{1} \\ a_{2} \\ a_{3} \\ ... \\ a_{n + 1} \end{matrix}) \\ = (\begin{matrix} x_{1}^{n} & x_{2}^{n} & x_{3}^{n} & ... & x_{m}^{n} \\ x_{1}^{n - 1} & x_{2}^{n - 1} & x_{3}^{n - 1} & ... & x_{m}^{n - 1} \\ x_{1}^{n - 2} & x_{2}^{n - 2} & x_{3}^{n - 2} & ... & x_{m}^{n - 2} \\ ... & ... & ... & ... & ... \\ 1 & 1 & 1 & ... & 1 \end{matrix}) (\begin{matrix} y_{1} \\ y_{2} \\ y_{3} \\ ... \\ y_{m} \end{matrix}) \\ (V^{T} V) a = V^{T} y \end{array}$

Donde V es una matriz del tipo Vandermonde

Ejemplo

Una experiencia que se puede llevar a cabo con la ayuda de un cronómetro es la de establecer una relación entre la lectura n del contador del reproductor de la casete y el tiempo t transcurrido. Vamos a comprobar que esta relación no es lineal

Se sugiere al lector que analice el comportamiento de su reproductor de casete y complete una tabla como la siguiente, y represente los datos en una gráfica semejante a la figura más abajo

n/100	0	1	2	3	4	5	6	7	7.44
t(min)	0	4.03	8.12	14.23	20.33	27.1	34.53	42.63	46.43

Ajustar el conjunto de pares de datos de la tabla de la derecha a un polinomio de segundo grado a₁x²+a₂x+a₃.

x=[0,1,2,3,4,5,6,7,7.44];
y=[0,4.03,8.12,14.23,20.33,27.1,34.53,42.63,46.43];
n=2; %polinomio de segundo grado
V=zeros(length(x),n+1);
for i=1:n+1
    V(:,i)=x.^(n+1-i);
end
p=(V'*V)\(V'*y');

%gráficos
hold on
plot(x,y,'bo', 'markersize',4,'markeredgecolor','b','markerfacecolor','b')
f=@(x) polyval(p,x);
fplot(f,[x(1),x(end)],'r')
xlabel('x')
ylabel('y')
grid on
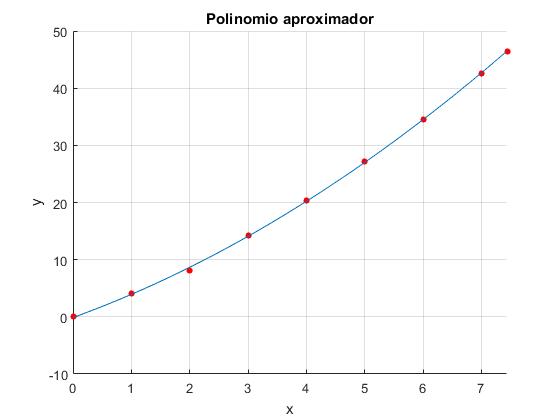
title('Polinomio aproximador')
hold off

En la ventana de comandos corremos el script y nos aparece el vector p que contiene los coeficientes a_1,a₂, a₃ del polinomio

Alternativamente, escribimos el sistema de ecuaciones

$\begin{array}{l} {\begin{cases} s_{1} a_{1} + s_{2} a_{2} + .... s_{n} a_{n} + s_{n + 1} a_{n + 1} = b_{1} \\ s_{2} a_{1} + s_{3} a_{2} + .... s_{n + 1} a_{n} + s_{n + 2} a_{n + 1} = b_{2} \\ ....... \\ s_{n + 1} a_{1} + s_{n + 2} a_{2} + .... s_{2 n} a_{n} + s_{2 n + 1} a_{n + 1} = b_{n + 1} \end{cases} \\ s_{k} = \sum_{j = 1}^{m} x_{j}^{2 n + 1 - k} k = 1...2 n + 1 \\ b_{k} = \sum_{j = 1}^{m} y_{j} x_{j}^{n + 1 - k} k = 1... n + 1 \end{array}$

En forma matricial

$(\begin{matrix} s_{1} & s_{2} & ... & s_{n} & s_{n + 1} \\ s_{2} & s_{3} & .... & s_{n + 1} & s_{n + 2} \\ ... & ... & ... & ... & ... \\ s_{n} & s_{n + 1} & ... & s_{2 n - 1} & s_{2 n} \\ s_{n + 1} & s_{n + 2} & ... & s_{2 n} & s_{2 n + 1} \end{matrix}) (\begin{matrix} a_{1} \\ a_{2} \\ ... \\ a_{n} \\ a_{n + 1} \end{matrix}) = (\begin{matrix} b_{1} \\ b_{2} \\ ... \\ b_{n} \\ b_{n + 1} \end{matrix})$

function p=pol_regresion(x,y,n) 
    s=zeros(2*n+1,1);
    b=zeros(n+1,1);
    A=zeros(n+1);
    for k=1:2*n+1
        s(k)=sum(x.^(2*n+1-k));
    end
    %elementos de la matriz A de las incógnitas
    for i=1:n+1
        for j=1:n+1 
            A(i,j)=s(i+j-1);
        end
    end
    %vector de los términos independientes
    for k=1:n+1
        b(k)=sum(y.*x.^(n+1-k));
    end
    %coeficientes del polinomio a1, a2... an, an+1
    p=A\b; 
end

A la función pol_regresion se le pasa los vectores x e y de datos el grado n del polinomio aproximador y devuelve los coeficientes del polinomio en el vector columna p.

La función calcula los elementos de la matriz A de las incógnitas, el vector b de los términos independientes y resuelve el sistema de n+1 ecuaciones con n+1 incógnitas mediante el operador división por la izquierda \.

Creamos un script con los datos y llamamos a la función pol_regresion

x=[0,1,2,3,4,5,6,7,7.44];
y=[0,4.03,8.12,14.23,20.33,27.1,34.53,42.63,46.43];
p=pol_regresion(x,y,2)

%gráficos
hold on
plot(x,y,'ro','markersize',4,'markerfacecolor','r')
y=@(x) polyval(p,x);
fplot(y,[x(1),x(end)])
xlabel('x')
ylabel('y')
grid on
title('Polinomio aproximador')
hold off