Ajuste de datos con MATLAB

Ajuste de datos con el operador, división por la izquierda \.

Conocidos los n pares de datos (x_i,y_i) i=1,2...n resolvemos el sistema de n ecuaciones para determinar las incógnitas, los coeficientes a_1,a₂, a₃ del polinomio que mejor ajusta

$\begin{array}{l} y = a_{1} x^{2} + a_{2} x + a_{3} \\ (\begin{matrix} y_{1} \\ y_{2} \\ ... \\ y_{n} \end{matrix}) = (\begin{matrix} x_{1}^{2} & x_{1} & 1 \\ x_{2}^{2} & x_{2} & 1 \\ ... & ... & ... \\ x_{n}^{2} & x_{n} & 1 \end{matrix}) (\begin{matrix} a_{1} \\ a_{2} \\ a_{3} \end{matrix}) \end{array}$

En el último ejemplo de la página anterior, tenemos n=9 pares de datos (x_i,y_i) que ajustamos a un polinomio de segundo grado. Resolvemos un sistema de nueve ecuaciones con tres incógnitas, con el operador \ (división por la izquierda)

x=[0,1,2,3,4,5,6,7,7.44]';
y=[0,4.03,8.12,14.23,20.33,27.1,34.53,42.63,46.43]';
M=[x.^2,x,ones(size(x))];
p=M\y %coeficientes del polinomio

hold on
plot(x,y,'ro','markersize',4,'markerfacecolor','r')
z=@(x) polyval(p,x);
fplot(z,[x(1),x(end)])
xlabel('x')
ylabel('y')
grid on
title('Polinomio aproximador')
hold off

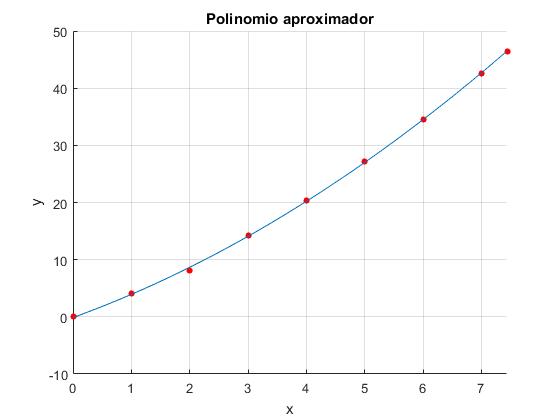
En la ventana de comandos vemos los valores de los coeficientes a_1,a₂, a₃ como elementos del vector p.

Ajuste de datos con polyfit

Para el ajuste de datos a un polinomio se utiliza la función MATLAB polifit, cuya sintaxis es la siguiente:

polyfit(x,y,n)

x, y, son los vectores de las abscisas y de las ordenadas de los datos, respectivamente
n, es el grado del polinomio al que se quieren ajustar los datos
p, es el vector de los coeficientes de dicho polinomio.

Para n=1 tenemos la regresión lineal. Si m es el número de datos, el polinomio pasa a través de todos los puntos si n=m-1. El grado n del polinomio no puede ser mayor que m-1.

En el ejemplo de la página precedente, se cambia la llamada a la función pol_regresion por la función MATLAB polyfit

x=[0,1,2,3,4,5,6,7,7.44];
y=[0,4.03,8.12,14.23,20.33,27.1,34.53,42.63,46.43];
p=polyfit(x,y,2)

%gráficos
hold on
plot(x,y,'ro','markersize',4,'markerfacecolor','r')
z=@(x) polyval(p,x);
fplot(z,[x(1),x(end)])
xlabel('x')
ylabel('y')
grid on
title('Polinomio aproximador')
hold off

En la ventana de comandos corremos el script y nos aparece el vector p que contiene los coeficientes a_1,a₂, a₃ del polinomio

p =    0.3446    3.7004   -0.1188

También se puede utilizar polyfit para realizar ajustes a una función potencial, exponencial, logarítmica, etc, tal como se muestra en el siguiente cuadro

Función	Llamada a polyfit
y=c·x^a	p=polyfit(log(x), log(y),1)
y=c·e^ax	p=polyfit(x, log(y),1)
y=a·ln(x)+c	p=polyfit(log(x),y,1)
$y = \frac{1}{a x + c}$	p=polyfit(x,1./y,1)

El primer elemento del vector p devuelto por polyfit, p(1) guarda el parámetro a y el segundo elemento, p(2) guarda el parámetro c.

En el ejemplo de la página anterior, ajuste a una función potencial

x=[10 20 30 40 50 60 70 80];
y=[1.06 1.33 1.52 1.68 1.81 1.91 2.01 2.11];
p=polyfit(log10(x),log10(y),1);
fprintf('exponente a= %2.3f\n',p(1));
fprintf('coeficiente c = %3.3f\n',(10^p(2)));

hold on
plot(x,y,'ro','markersize',4,'markerfacecolor','r')
z=@(x) (10^p(2))*x.^p(1);
fplot(z,[x(1),x(end)])
xlabel('x')
ylabel('y')
grid on
title('Regresión potencial')
hold off

Corremos el script en la ventana de comandos

exponente a= 0.331
coeficiente c = 0.495

En el ejemplo de la página anterior, ajuste a una función exponencial.

x=[12 41 93 147 204 264 373 509 773];
y=[930 815 632 487 370 265 147 76 17];
p=polyfit(x,log(y),1);
fprintf('exponente a= %2.3f\n',p(1));
fprintf('coeficiente c = %3.3f\n',exp(p(2)));

hold on
plot(x,y,'ro','markersize',4,'markerfacecolor','r')
z=@(x) exp(p(2))*exp(x*p(1));
fplot(z,[x(1),x(end)])
xlabel('x')
ylabel('y')
grid on
title('Regresión exponencial')
hold off

Corremos el script en la ventana de comandos

exponente a= -0.005
coeficiente c = 1036.896

Ajuste de forma interactiva

Función lineal

Determinar la recta de regresión para la siguiente tabla de datos, tomadas de una experiencia

x	0.05	0.1	0.15	0.2	0.25	0.3	0.35	0.4
y	0.25	0.42	0.58	0.72	0.85	0.98	1.10	1.12

Vamos a realizar el ajuste de datos de forma interactiva en la ventana Figure Window. En la ventana de comandos escribimos

>> x=[0.05 0.1 0.15 0.2 0.25 0.3 0.35 0.4];
>> y=[0.25 0.42 0.58 0.72 0.85 0.98 1.1 1.2];
>> plot(x,y,'ro','markersize',4,'markerfacecolor','r')

Aparece la representación gráfica de los puntos

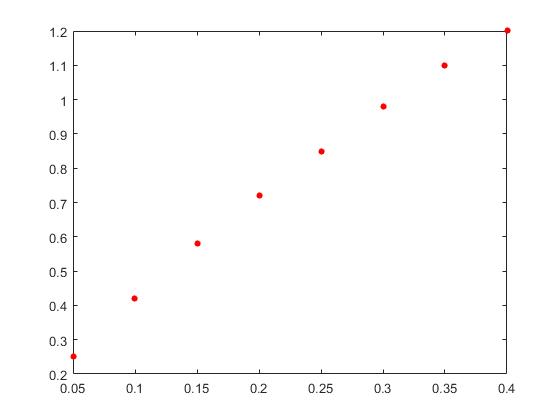
Seleccionamos en el menú Tools/Basic Fitting, y activamos la casilla linear (polinomio de grado 1) en el primer panel titulado Plot fits. Observamos en la ventana Figure 1 la recta que mejor ajusta a los datos experimentales. La ecuación de dicha recta se muestra en la ventana gráfica, activando la casilla Show equations

Añadimos una rejilla, etiquetas a los ejes y un título al gráfico en la ventana de comandos

>> grid on
>> xlabel('x')
>> ylabel('y')
>> title('Experiencia')

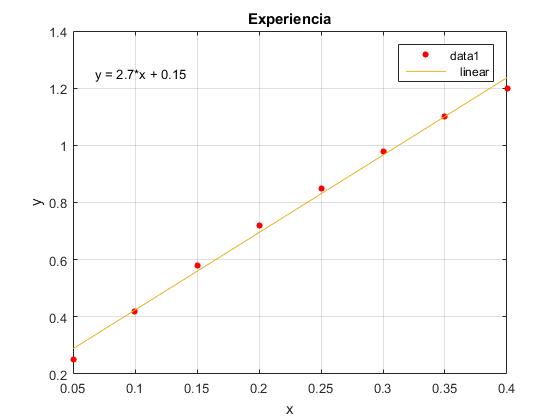
Ampliamos el cuadro de diálogo pulsando en el botón con la flecha inferior derecha -->. Seleccionamos en el segundo panel titulado Numerical results Fit/linear y nos aparece

y = p1*x + p2

Coefficients:
  p1 = 2.7095
  p2 = 0.15286

Pulsamos el botón con la flecha --> para ampliar otra vez el cuadro de diálogo, introducimos un valor o una expresión para ser evaluada pulsando el botón Evaluate en el tercer panel titulado Find y=f(x).

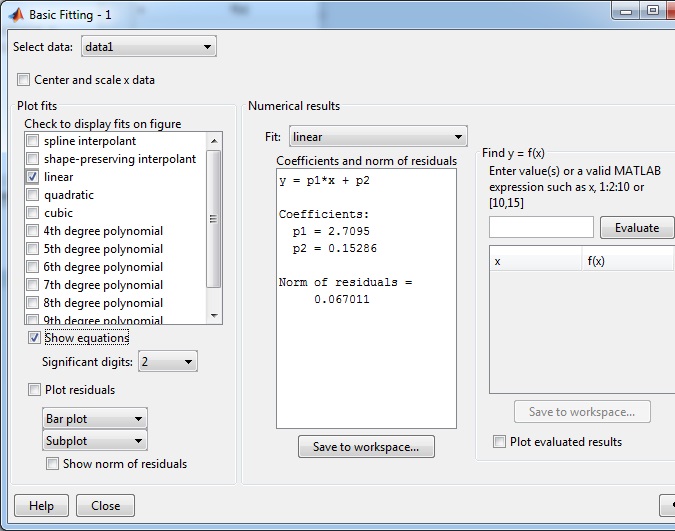
El ajuste de datos de forma interactiva en la ventana Figure Window admite muchas posibilidades, que se pueden consultar en el sistema de ayuda (Help).

Función de Gauss

Una función de Gauss centrada en x₀ tiene la forma

$\begin{array}{l} f (x) = C \exp (- \frac{{(x - x_{0})}^{2}}{2 σ^{2}}) \\ f (x) = C \exp (- b {(x - x_{0})}^{2}) \end{array}$

El parámetro σ está relacionado con la anchura de dicha función

Tomando logaritmos

$\begin{array}{l} \ln (f (x)) = \ln C - b {(x - x_{0})}^{2} \\ \ln (f (x)) = - b x^{2} + 2 b x_{0} x - b x_{0}^{2} + \ln C \\ y = a_{2} x^{2} + a_{1} x + a_{0}, {\begin{cases} a_{2} = - b \\ a_{1} = 2 b x_{0} \\ a_{0} = - b x_{0}^{2} + \ln C \end{cases} \end{array}$

Una vez que obtenemos los coeficientes del polinomio de segundo grado que mejor ajustan, calculamos los parámetros C, x₀ y σ

Se ha tomado los siguientes datos

x	31	32	33	34	35	36	37	38	39	40	41	42	43	44	45	46	47
y	11	27	60	118	206	319	440	539	586	565	484	368	249	149	79	38	16

x=31:47;
y=[11,27,60,118,206,319,440,539,586,565,484,368,249,149,79,38,16];
plot(x,log(y),'ro','markersize',3,'markerfacecolor','r')
grid on
xlabel('x')
ylabel('ln(y)')
title('Ajuste a una función de Gauss')

En el menú seleccionamos Tools/Basic Fitting. Aparece el cuadro de diálogo

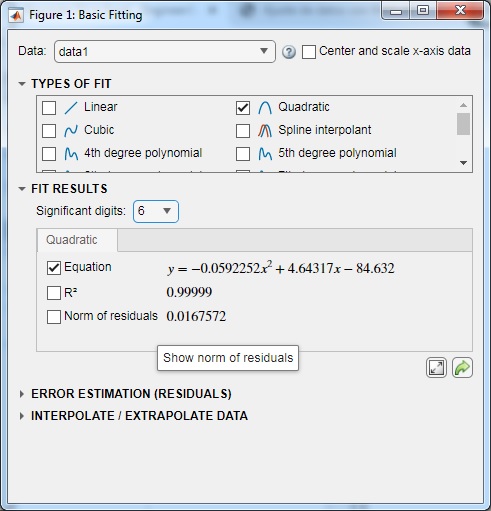
Activamos la casilla Quadratic y cambiamos en Significant digits, el valor por defecto y lo establecemos en 6. Aparece la figura

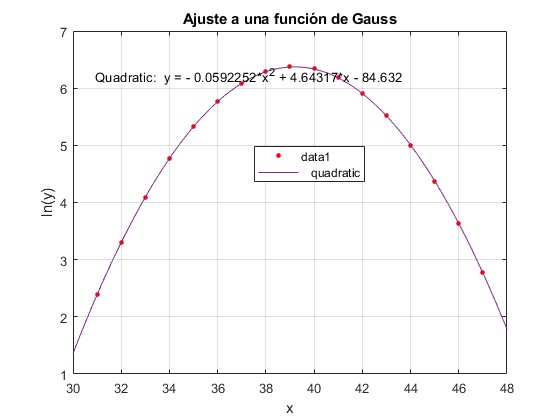
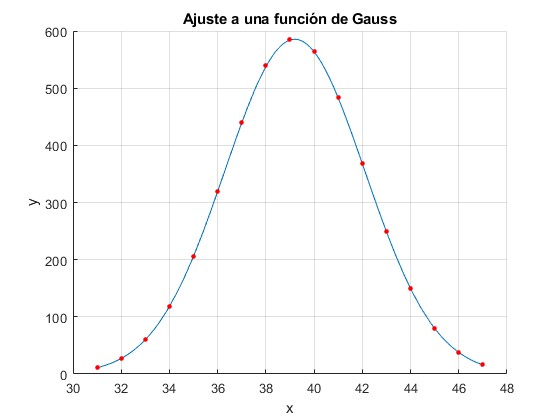
Representamos los datos experimentales y la función de Gauss con C=585.4921, x₀=39.1993 y b=0.0592252 o bien, σ=2.9056

x=31:47;
y=[11,27,60,118,206,319,440,539,586,565,484,368,249,149,79,38,16];
a2=-0.0592252;
a1=4.64317;
a0=-84.632;

b=-a2;
x0=a1/(2*b);
C=exp(a0+b*x0^2);
f=@(x) C*exp(-b*(x-x0).^2);
hold on
fplot(f,[31,47])
plot(x,y,'ro','markersize',3,'markerfacecolor','r')
hold off
grid on
xlabel('x')
ylabel('y')
title('Ajuste a una función de Gauss')

>> C
C =  585.4921
>> x0
x0 =   39.1993
>> sigma=sqrt(1/(2*b))
sigma =    2.9056

Referencias

Gaussian fit in Excel

Ejemplos en el curso de Física

menú Tools/Basic fitting. Función polyfit

Medida de la velocidad en un movimiento rectilíneo y uniforme

Medida de la aceleración en un movimiento rectilíneo y uniformemente acelerado

Movimiento de la cinta de una casete

Medida de la constante de un muelle

Medida del módulo de elasticidad

Medida del módulo de cizallamiento

Flexión de una viga en voladizo (I)

El muelle elástico

Péndulo de torsión

El péndulo simple

Oscilaciones amortiguadas

Oscilaciones amortiguadas por una fuerza de módulo constante.Plano inclinado

Velocidad de propagación de un movimiento ondulatorio

El sonido

El prisma de vidrio

Optica no paraxial de una lente esférica

La ley de Snell de la refracción

Optica paraxial

Efusión de un gas

Ley del enfriamiento de Newton

La lámpara incandescente

Vaciado de un depósito abierto

Medida de la viscosidad de un líquido

Medida de la viscosidad de un líquido mediante dos vasos comunicantes

El tubo-capilar

Descarga de un condensador

Fuerza magnética sobre conductor rectilíneo. La balanza de corriente

Campo magnético producido por un imán

Función de distribución de Weibull

Energía producida por un aerogenerador

Medida del coeficiente cinético (II)

x	31	32	33	34	35	36	37	38	39	40	41	42	43	44	45	46	47
y	11	27	60	118	206	319	440	539	586	565	484	368	249	149	79	38	16

x	31	32	33	34	35	36	37	38	39	40	41	42	43	44	45	46	47
y	11	27	60	118	206	319	440	539	586	565	484	368	249	149	79	38	16

x	31	32	33	34	35	36	37	38	39	40	41	42	43	44	45	46	47
y	11	27	60	118	206	319	440	539	586	565	484	368	249	149	79	38	16