Energía producida por un aerogenerador
Energía por unidad de tiempo suministrada por el viento
La energía por unidad de tiempo (potencia) del viento cuando pasa a través de un área A perpendicular a la dirección del viento es
A=πR2 es el área barrida por las palas del aerogerador de longitud R, ρ=1.225 kg/m3 es la densidad del aire a nivel del mar a 15°C y x la velocidad del viento.
Medida de las velocidades del viento
Calculamos el valor medio de Pv directamente de las medidas de la velocidad del viento o de la tabla de velocidades y frecuencias.
Función de distribución de Weibull
Si hemos establecido un modelo estadístico que describa las medidas de las velocidades y sus frecuencias mediante una función continua f(x), el valor medio de la potencia para la función de distribución de Weibull
Si la función de Weibull se ajusta perfectamente a los datos del viento, la potencia calculada mediante esta fórmula será similar a la calculada directemente de los valores de la velocidad del viento. Cuanto mayor sea la diferenica entre los dos resultados peor será el ajuste de la función de distribución de Weibull a las medidas de las velocidades del viento.
Función de distribución de Rayleigh
El valor medio de la energía por unidad de tiempo del viento para la función de distribución de Rayleigh es
Donde hemos utilizado el resultado de la integral
Elaboramos un script para calcular la potencia por unidad de área <P>/A en W/m2 por los tres procedimientos
clear,clc
velocidad=xlsread('WhiteDeer2013','Mar','F2:F745');
%interpolar si es necesario
if any(isnan(velocidad)) %si hay algún NaN
x=1:length(velocidad);
i=find(~isnan(velocidad));
velocidad=interp1(x(i),velocidad(i),x);
end
%parámetros c y k de la función de Weibull
x=0.5:1:max(velocidad);
horas=hist(velocidad,x);
%convierte a frecuencias y ajusta a la función de Weibull
frec=horas/sum(horas);
f=@(a,x) (a(1)/a(2))*((x/a(2)).^(a(1)-1)).*exp(-(x/a(2)).^a(1));
a0=[2 8]; %valor inicial de los parámetros
af=nlinfit(x,frec,f,a0);
k=af(1), c=af(2)
fprintf('Parámetros Weibull: k=%1.4f, c=%1.4f\n',k,c)
%directamente de los datos de las velocidades del viento
potencia=0.5*1.225*sum(velocidad.^3)/length(velocidad);
fprintf('Potencia, directamente de las medidas: %3.1f\n',potencia);
media=mean(velocidad);
%función de distribución de Weibull
potencia=0.5*1.225*media^3*gamma(1+3/k)/(gamma(1+1/k)^3);
fprintf('Potencia, función Weibull: %3.1f\n',potencia);
%función de distribución de Rayleigh
potencia=0.5*1.225*6*media^3/pi;
fprintf('Potencia, función Rayleigh: %3.1f\n',potencia);
Parámetros Weibull: k=2.0486, c=9.4165 Potencia, directamente de las medidas: 586.5 Potencia, función Weibull: 624.0 Potencia, función Rayleigh: 638.9
Energía suministrada por el aerogerador
Descargamos un fichero Excel que contiene los datos de la curva de potencia de varios modelos de aerogenerador de distintos fabricantes desde el sitio Idaho National Laboratory
Elegimos el fichero del fabricante español Acciona que contiene el fichero Excel pc_acciona.xls (alternativamente, se descarga en este enlace). Este fichero tiene varias hojas que describen las curvas de potencia de diferentes modelos, elegimos la primera correspondiente al modelo AW 70-1500 Class I. Los datos de la velocidad del viento van 0, 0.5, 1.5... 25 m/s vienen recogidos en la columna A y las correspondientes potencias en kW en la columna B desde la fila 2 a la 52. Leemos esta columna mediante el comando
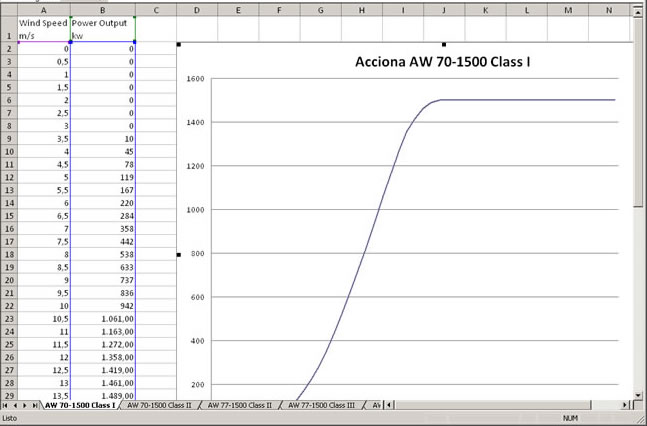
Creamos un script para cargar los datos de la hoja AW 70-1500 Class I, columna B desde la fila 2 a la 52 y representamos la curva de potencia del aerogenerador.
clear,clc
potencia=xlsread('pc_acciona','AW 70-1500 Class I','B2:B52');
x=0:0.5:25; %velocidad
hold on
plot(x,potencia,'ro','markersize',3,'markerfacecolor','r')
plot(x, potencia,'b')
title('Curva de potencia de un aerogenerador');
ylim([-10 1550])
xlabel('velocidad')
ylabel('potencia')
grid on
hold off
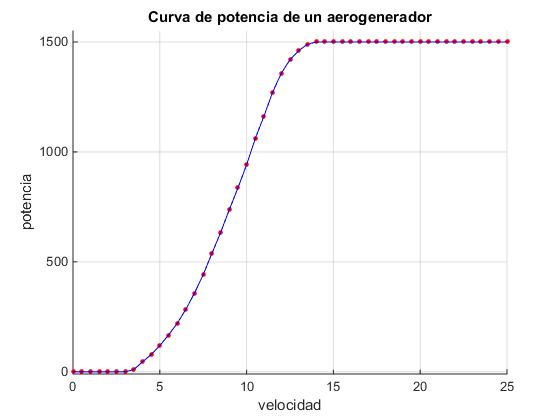
Si Pe(x) es la función que describe la potencia del aerogerador en función de la velocidad x. La potencia media <Pw> producida por el aerogerador se obtiene
Calculamos este dato a partir de la tabla de velocidades del viento xj y sus correspondienets frecuencias fj
Para hacer el producto elemento a elemento del vector
Este script realiza el cálculo de la potencia suministrada por el generador directamente a partir de los datos de las velocidades del viento y de la curva de potencia del aerogenerador.
clear,clc
potencia=xlsread('pc_acciona','AW 70-1500 Class I','B2:B52');
x=0:0.5:25; %velocidad
velocidad=xlsread('WhiteDeer2013','Mar','F2:F745');
%interpolar si es necesario
if any(isnan(velocidad)) %si hay algún NaN
x=1:length(velocidad);
i=find(~isnan(velocidad));
velocidad=interp1(x(i),velocidad(i),x);
end
%histograma
horas=hist(velocidad,x);
%convierte a frecuencias
frec=horas/sum(horas); %potencia es vector columna y frec es vector fila
res=sum(frec*potencia); %potencia por unidad de area
fprintf('La potencia por unidad de área es %3.1f\n',res)
La potencia por unidad de área es 643.6
El aerogenerador produce energía en un intervalo de velocidades mínima (cut-in) x0 y máxima (cut-out) x1. A una velocidad intermedia xr (rated) alcanza la máxima potencia Pr que es casi constante. Para el aerogenerador de la marca Acciona que nos ha servido de ejemplo: Pr=1500, x0=3.0, xr=14 y x1=25 m/s
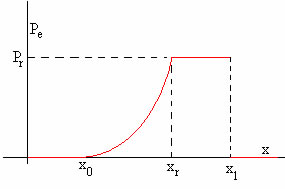
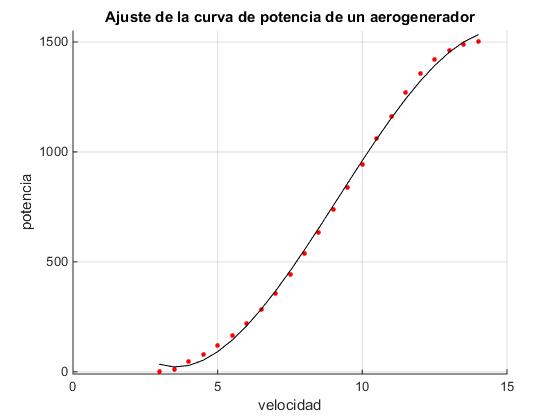
Se pueden establecer varios tipos de ecuaciones que describen la región intermedia entre x0 y xr. Se puede ajustar a polinomios de varios grados u otro tipo de función. En nuestro caso hemos ajustado los datos de la potencia del aerogenerador comprendidos entre x0 y xr mediante un polinomio de tercer grado utilizando la función
Finalmente, calculamos la potencia media por unidad de área que produce el aerogenerador con el régimen de vientos del mes de Marzo en la localidad en la que se han tomado las medidas.
Este script traza la gráfica y calcula las integrales definidas empleando la función
clear,clc
Pr=1500; x0=3.0;xr=14;x1=25; %datos de la curva de potencia
k=2.0486; c=9.4165; %parámetros de ajuste de la función de Weibull
potencia=xlsread('pc_acciona','AW 70-1500 Class I','B2:B52');
x=0:0.5:25;
pot=potencia(x>=x0 & x<=xr);
hold on
x=x0:0.5:xr;
plot(x,pot,'ro','markersize',3,'markerfacecolor','r')
title('Ajuste de la curva de potencia de un aerogenerador');
axis([0 15 -10 1550])
xlabel('velocidad')
ylabel('potencia')
grid on
%ajuste
p=polyfit(x,pot',3); %ajuste a un polinomio de tercer grado
yp=polyval(p,x);
plot(x,yp,'k')
hold off
%cálculo de la potencia media
f=@(x) (k/c)*((x/c).^(k-1)).*exp(-(x/c).^k); %función de Weibull
h=@(x) f(x).*polyval(p,x);
power=quad(h,x0,xr)+Pr*quad(f,xr,x1);
fprintf('La potencia media es: %3.1f\n',power)
La potencia media es: 642.9

