Movimiento de una partícula que desliza a lo largo de una varilla que gira con velocidad angular constante.
La varilla es un segmento de recta
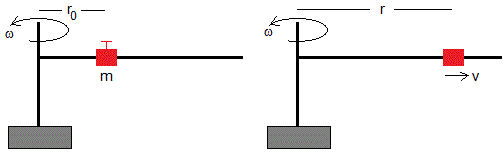
Sea una varilla que gira con velocidad angular constante ω. Una partícula está sujeta a una distancia r0 del eje. Se suelta y desliza a lo largo de la varilla. Se pide calcular la velocidad de partícula cuando se encuentra a una distancia r>r0.
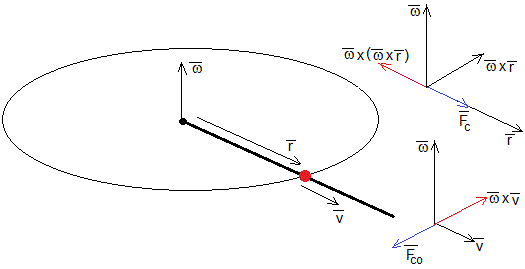
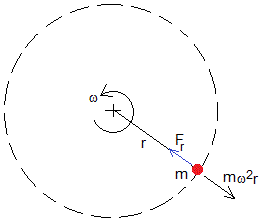
En el sistema de referencia en rotación (no inercial), las fuerzas sobre la partícula son
la fuerza centrífuga , cuya dirección es radial
la fuerza de Coriolis, , cuya dirección es perpendicular a la dirección radial. No contribuye al movimiento de la partícula, se anula con una fuerza de reacción de sentido contrario, proporcionada por la varilla
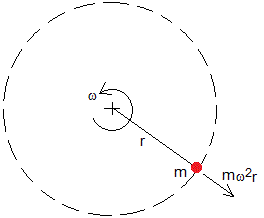
Cuando la partícula de masa m se encuentra a una distancia r del eje, experimenta una fuerza centrífuga mω2r. La ecuación del movimiento en la dirección radial es
La solución de la ecuación diferencial
Los coeficientes A y B se determinan a partir de las condiciones iniciales: en el instante t=0, parte del reposo dr/dt=0, en la posición r=r0.
La distancia de la partícula al eje r y la velocidad radial dr/dt de la partícula en función del tiempo t son
La velocidad de la partícula tiene dos componenentes: la velocidad en la dirección radial dr/dt y la velocidad en la dirección tangencial rω: su módulo es
Por ejemplo, si la longitud de la varilla es r=2r0 y gira con velocidad angular ω=1 rad/s
El tiempo que tarda en salir por su extremo es
El módulo de la velocidad de la partícula en este instante es
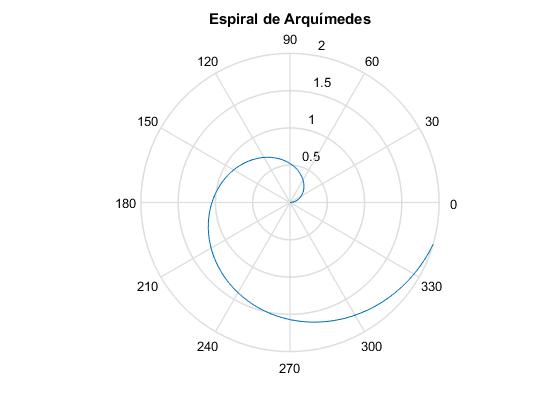
Espiral de Arquímedes, θ=n·r
Supongamos ahora que la forma de la varilla está dada por la función θ=n·r en el instante t=0, siendo n una constante. Por ejemplo, para n=3 la forma de una varilla de longitud r=2 es
r=linspace(0,2,100);
n=3;
polar(n*r,r)
title('Espiral de Arquímedes')
Ecuación del movimiento
La velocidad angular dθ/dt de la partícula cuando la varilla gira con velocidad angular constante ω es
La energía cinética de la partícula es
La lagrangiana es L=Ek. La ecuación del movimiento en la dirección radial es
Para calcular la distancia de la partícula al eje r en función del tiempo t, se resuelve esta ecuación diferencial por procedimientos numéricos con las siguientes condiciones iniciales: t=0, r=r0, dr/dt=0
Conocido r en función de t, el ángulo que forma la partícula será, θ=n·r+ωt. La posición de la partícula en coordenadas polares es (r, θ)
Velocidad radial
Podemos integrar esta ecuación diferencial, teniendo en cuenta la regla
La ecuación del movimiento en la dirección radial se escribe
Integramos, sabiendo que para r=r0, dr/dt=0, obteniendo la velocidad en la dirección radial
El módulo de la velocidad de la partícula, cuando se encuentra en la posición r es
Representamos la velocidad final v en función de n, para r0=1, r=2, siendo la velocidad angular constante de la varilla ω=1 rad/s
r0=1; %posición inicial
r=2; %posición final
w=1; %velocidad angular de la varilla
v=@(n) w*sqrt(2*r^2-r0^2+2*r^2*n.*sqrt((r^2-r0^2)./(n.^2*r^2+1)));
plot(0:5,v(0:5), 'ro','markersize',3,'markeredgecolor','r','markerfacecolor','r')
grid on
set(gca,'XTick',0:5)
set(gca,'XTickLabel',{'0','1','2','3','4','5'})
xlabel('n')
ylabel('v')
title('Velocidad final')
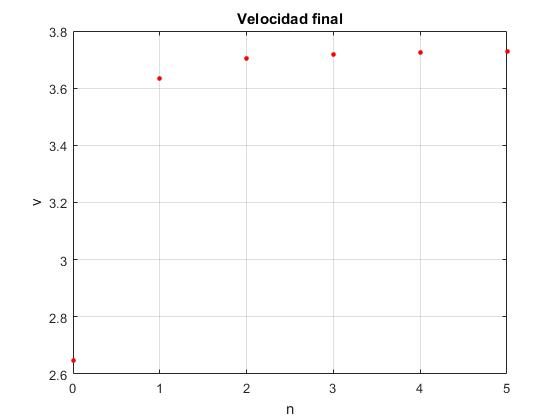
La velocidad final aumenta con n alcanzando un límite constante cuando n→∞
>> w*(r+sqrt(r^2-r0^2)) ans = 3.7321
Tiempo de viaje
El tiempo que tarda en ir desde la posición inicial r0 a la posición final r es
Calculamos el tiempo t que tarda la partícula en desplazarse desde r0=1 a r=2, deslizando a lo largo de una varilla en forma de espiral de Arquímedes con n=3, sabiendo que la velocidad angular constante de la varilla ω=1 rad/s. Resolvemos la integral por procedimientos numéricos
r0=1; %posición inicial r=2; %posición final w=1; %velocidad angular de la varilla n=3; %forma en espiral de la varilla f=@(r) sqrt((n^2*r.^2+1)./(r.^2-r0^2)); t=integral(f,r0,r)/w
t = 5.3674
Actividades
Se introduce
- El parámetro n, de la ecuación de la espiral de Arquímedes, θ=n·r, en el control titulado n
- Se ha fijado la posición inicial de partida, r0=1
- Se ha fijado la velocidad angular de rotación de la varilla, ω=1
Cuando n=0, tenemos un segmento de recta, que es el caso más simple, estudiado en el primer apartado
Se pulsa el botón titulado Nuevo
En la esquina superior izquierda, se porporcionan los datos de
- El tiempo, t
- La posición de la partícula en coordenadas polares, (r, θ)
- La velocidad radial, dr/dt
La varilla tiene la forma, θ=f(r)
Supongamos que la ecuación de la varilla en el instante t=0 es θ=f(r). La velocidad angular dθ/dt de partícula cuando la varilla gira con velocidad angular constante ω es
La energía cinética de la partícula es
La lagrangiana es L=Ek. La ecuación del movimiento en la dirección radial es
Comprobamos que para f(r)=n·r, df/dr=n, d2f/dr2=0, espiral de Arquímedes, obtenemos la ecuación diferencial del apartado anterior.
Salvo, casos especiales, como la espiral logarítmica, que estudiremos a continuación, se resolverá esta ecuación diferencial por procedimientos numéricos (véase la espiral de Arquímedes) con las siguientes condiciones iniciales: t=0, r=r0, dr/dt=0
Velocidad radial
La ecuación del movimiento en la dirección radial se escribe
Integramos, sabiendo que para r=r0, dr/dt=0, obteniendo la velocidad en la dirección radial
El módulo de la velocidad de la partícula, cuando se encuentra en la posición r es
La velocidad final aumenta con la pendiente de la varilla df/dr alcanzando un límite constante cuando df/dr→∞
Representamos la velocidad final de la partícula v en función de la pendiente df/dr de la varilla en la posición final r. Sea la posición inicial r0=1 y la final r=2, la velocidad angular constante de la varilla es ω=1 rad/s
r0=1; %posición inicial
r=2; %posición final
w=1; %velocidad angular de la varilla
v=@(p) w*sqrt(2*r^2-r0^2+2*r^2*p.*sqrt((r^2-r0^2)./(p.^2*r^2+1)));
fplot(v, [0,5])
grid on
xlabel('df/dr')
ylabel('v')
title('Velocidad final')
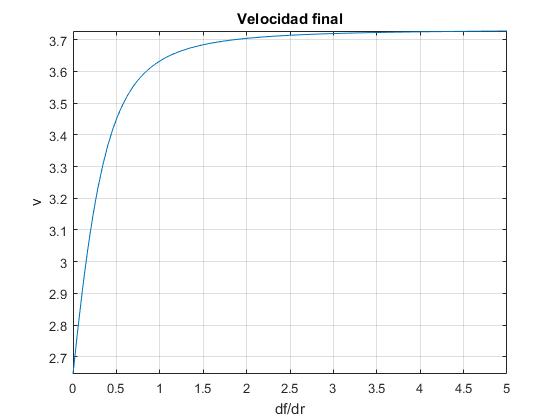
La velocidad final constante v∞ vale
>> w*(r+sqrt(r^2-r0^2)) ans = 3.7321
Tiempo de viaje
El tiempo que tarda en ir desde la posición inicial r0 a la posición final r es
Espiral logarítmica, θ=D·ln(r/r0)
Supongamos ahora que la forma de la varilla está dada por la función θ=D·ln(r/r0) en el instante t=0, siendo D una constante. Por ejemplo, en el instante t=0, θ=0, la partícula se encuentra en r0=1; cuando θ=3π/2, se encuentra en r=4. Entonces
Representamos la varilla en el instante t=0,
r0=1;
r=linspace(r0,4,100);
D=3*pi/(2*log(4));
polar(D*log(r),r)
title('Espiral logarítmica')
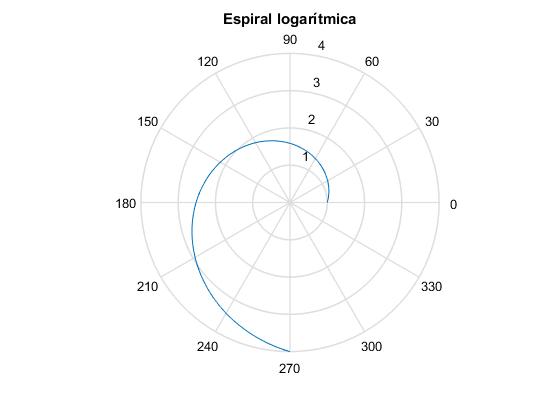
Para f(r)=D·ln(r/r0), la velocidad en la dirección radial, dr/dt es
El tiempo de viaje
>> r0=1; >> D=3*pi/(2*log(4)); >> r=4; >> w=1; >> sqrt(1+D^2)*acosh(r/r0)/w ans = 7.3114Ecuación del movimiento
Hemos deducido la ecuación del movimiento para θ=f(r)
Se simplifica para una espiral logarítmica
La solución, ya estudiada en el primer apartado, es
Los coeficientes A y B se determinan a partir de las condiciones iniciales: en el instante t=0, parte del reposo dr/dt=0, en la posición r=r0.
La distancia de la partícula al eje r y la velocidad radial dr/dt de la partícula en función del tiempo t son
Conocido r en función de t, el ángulo que forma la partícula será, θ=D·ln(r/r0)+ωt. La posición de la partícula en coordenadas polares es (r, θ)
ActividadesSe introduce
- El parámetro D, de la ecuación de la espiral logarítmica, θ=D·ln(r/r0), en el control titulado D
- Se ha fijado la posición inicial de partida r0=1
- Se ha fijado la velocidad angular de rotación de la varilla, ω=1
Se pulsa el botón titulado Nuevo
En la esquina superior izquierda, se porporcionan los datos de
- El tiempo, t
- La posición de la partícula en coordenadas polares, (r, θ)
- La velocidad radial, dr/dt
Forma óptima de la varilla
Vamos a encontrar la forma de la varilla θ=f(r), de modo que el tiempo empleado en recorrerla desde la posición inicial r0 a la final r sea mínimo
Dada la función F(r, df/dr), tenemos que encontrar la función θ=f(r) que hace que la integral
denominado funcional, sea un extremo
La función f(r) deberá cumplir la ecuación de Euler-Lagrange
El funcional F no depende de f, solamente de su derivada df/dr. El primer término es nulo, por tanto, el término entre paréntesis es constante
Tiempo de viaje
El tiempo que tarda en desplazarse desde r0 a r es
Se ha sustituído la variable r2 por x. Tenemos una integral del tipo
Utilizamos Math Symbolic de MATLAB para obtener el integrando
>> syms a positive; >> syms x b c; >> int(1/sqrt(-a*x^2+b*x+c),x) ans =-asin((b - 2*a*x)/(b^2 + 4*a*c)^(1/2))/a^(1/2)
Hay otra solución equivalente que nos da un resultado más sencillo. Se hace el cambio de variable
La integral se expresa en términos de la variable v
Se hace ahora el cambio
La integral es inmediata
El resultado final
Ecuación de la forma de la varilla, θ=f(r)
Integrando df/dr obtenemos la ecuación de la varilla, θ=f(r)
Es una integral del tipo
Utilizamos Math Symbolic de MATLAB para obtener el integrando
>> syms x; >> syms a positive; >> syms b positive; >> int(sqrt((x^2-a^2)/(a^2-b*x^2))/x,x) ans = atan(b^(1/2)*((a^2 - x^2)/(- a^2 + b*x^2))^(1/2))/b^(1/2) - atan(((a^2 - x^2)/(- a^2 + b*x^2))^(1/2))
Hay otra solución equivalente que nos da un resultado más sencillo. Se hace el cambio de variable
La integral se expresa en términos de la variable u
La primera integral es inmediata
Para resolver la segunda deshacemos los cambios, expresando la variable u en términos de r
Esta integral ya la hemos resuelto, en el apartado 'Tiempo de viaje'. La suma de los dos integrales es
Calculamos el parámetro C de modo que la velocidad sea máxima, es decir, cuando la derivada de df/dr de f(r) sea infinita en la posición final r.
Representamos la forma de la varilla θ=f(r) en el instante t=0, desde la posicón inicial r0=1, hasta r=4. Primero calculamos el parámetro C mediante la fórmula anterior
r0=1; %posición inicial
C=4/sqrt(15);
%f=@(r) atan(sqrt(1-1/C^2)*sqrt((r.^2-r0^2)./(r0^2-(1-1/C^2)*r.^2)))
/sqrt(1-1/C^2)-atan(sqrt((r.^2-r0^2)./(r0^2-(1-1/C^2)*r.^2)));
g=@(r) sqrt(C^2/(C^2-1))*asin(sqrt(C^2-1)*sqrt(r.^2-r0^2)/r0)-
asin(C*sqrt(r.^2-r0^2)./r);
r=linspace(r0,4,300);
%polar(f(r),r)
polar(g(r),r)
title('Forma óptima')
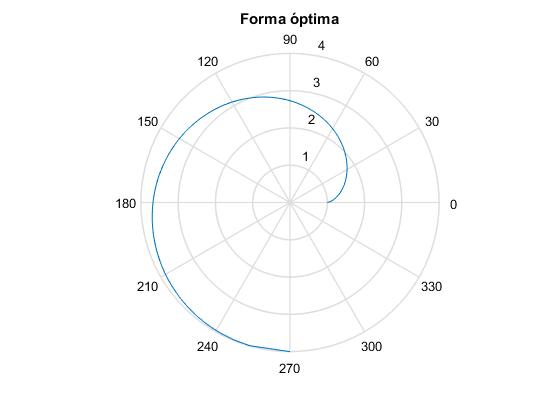
Obtenemos la misma representación gráfica, con las dos expresiones equivalentes de f(r)
El tiempo que tarda en desplazarse desde r0=1, a r=4, para esta trayectoria es
r=4; %posición final r0=1; %posición inicial w=1; %velocidad angular C=r/sqrt(r^2-r0^2); %parámetro %tiempo t=asin(sqrt(C^2-1)*sqrt(r^2-r0^2)/r0)/(w*sqrt(C^2-1)); %expresión equivalente a=1-1/C^2; b=r0^2*(2-1/C^2); c=-r0^4; t1=(-asin((b-2*a*r^2)/sqrt(b^2+4*a*c))+asin((b-2*a*r0^2)/sqrt(b^2+4*a*c))) /(2*w*C*sqrt(a));
>> t,t1 t = 6.0837 t1 = 6.0837
Obtenemos el mismo resultado empleando dos expresiones equivalentes del tiempo t
Fuerza de rozamiento proporcional a la velocidad
Estudiamos el primer caso, la varilla es un segmento de recta, añadiendo una fuerza de rozamiento porporcional a la velocidad. La ecuación del movimiento es
Recuerda a la ecuación de las oscilaciones amortiguadas pero en vez de tener signo positivo frente a ω2 es negativo.
Las raíces de la ecuación característica son:
La solución de la ecuación diferencial es
Los coeficientes A y B se determinan a partir de las condiciones iniciales. En el instante t=0, la partícula que desliza se encuentra en el origen r=0, y parte con velocidad dr/dt=v0.
El coeficiente B=0
La distancia r de la partícula al origen es
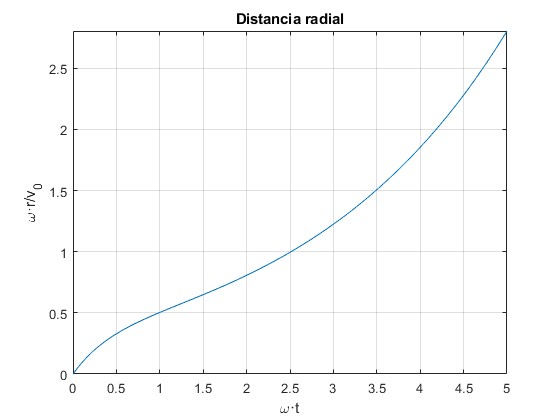
Expresamos esta ecuación, en términos de magnitudes adimensionales, R=ωr/v0, T=ωt
Representamos R en función del tiempo T para γ/ω=1
k=1; %gamma/omega
R=@(t) exp(-k*t).*sinh(sqrt(k^2+1)*t)/sqrt(k^2+1);
fplot(R, [0,5])
grid on
xlabel('\omega·t')
ylabel('\omega·r/v_0')
title('Distancia radial')
Referencias
Roland Ribberfors, Andreas Rietz. A study of a rotating rod carrying a collar using Lagrange's equation of motion and variational calculus. Eur. J. Phys. 21 (2000) pp. 151-157
C. E. Mungan. Bead Sliding on a Rotating Rod with Linear Drag. Summer 2021

