Un cuerpo desliza sobre la superficie de un cilindro en rotación
El problema de un cuerpo que desliza sobre una pista circular vertical ha sido ampliamente estudiado en la página titulada Movimiento en un bucle (I). Dependiendo de la velocidad inicial de la partícula en la parte inferior de la pista, ésta puede:
- Describir una trayectoria circular completa
- Ascender a lo largo de la pista hasta que su velocidad es cero, posición angular θ<90°
- Dejar de estar en contacto con la pista en el instante en el que la fuerza normal N es cero, θ>90°
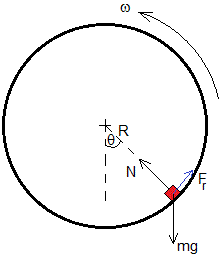
En esta página, la velocidad angular ω de rotación del cilindro de radio R será mayor que un valor mínimo, para asegurar que el cuerpo no cae y por tanto, completará la trayectoria circular vertical
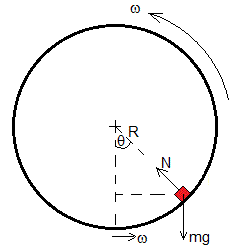
Las fuerzas sobre el cuerpo cuando su posición angular es θ son
El peso, mg
La reacción de la superficie cilíndrica N, cuya dirección es radial
La fuerza de rozamiento, Fr, cuya dirección es tangencial, que se opone a la velocidad relativa del cuerpo sobre la superficie cilíndrica, cuando desliza, o a la componente tangencial del peso si el cuerpo está en reposo relativo
Ecuación del movimiento en la dirección radial
Aplicando la ecuación de la dinámica del movimiento circular
N-mgcosθ=mω2R
Para que el cuerpo complete la trayectoria circular vertical, N>0, para cualquier ángulo θ. En particular, para θ=π, se tendrá que cumplir que ω2R>g. La velocidad angular ω deberá ser mayor que la mínima
Por ejemplo, si el radio del cilindro R=0.33 m, la velocidad angular mínima es ωm=5.45 rad/s
Si ω2R<g, la reacción N se anula para la posición angular del cuerpo θ>π/2
Por ejemplo, si ω=5 rad/s, θn=147° es la posición angular del cuerpo cuando empieza a caer, describiendo una trayectoria parabólica
Ecuación del movimiento en la dirección tangencial
La superficie interior del cilindro es rugosa, el coeficiente estático es μs. Supondremos que el coeficiente cinético es algo menor que el estático, μk=0.9μs
El cuerpo se deja en reposo en la parte inferior del cilindro, (su velocidad angular es la del cilindro, ω), en el instante t=0, cuando la posición angular del cuerpo es θ=0
Se plantean dos posibles casos:
- El cuerpo está en reposo relativo a la superficie cilíndrica
- El cuerpo desliza sobre la superficie cilíndrica
Cuerpo en reposo
Cuando el cuerpo está en reposo, la fuerza de rozamiento Fr es igual a la componente tangencial del peso, mgsinθ
Al girar el cilindro, la posición angular θ del cuerpo aumenta, la fuerza de rozamiento Fr aumenta, hasta que se hace igual al valor máximo μsN
El máximo de μs se calcula derivando el cociente respecto de θ e igualando a cero
Si ω=7.5 rad/s y R=0.33 m, el máximo de μs se produce para θm=122° y su valor es μm=0.6216. Si el coeficiente estático es mayor que el máximo, μs>0.6216, el cuerpo no desliza, siempre permenece en reposo relativo a la superficie cilíndrica
El movimiento más interesante del cuerpo se produce cuando el coeficiente estático μs<μm, que vamos a analizar a continuación
En lo que resta de página, utilizaremos los siguientes datos:
- Velocidad angular constante de rotación del cilindro, ω=7.5 rad/s
- Radio del cilindro, R=0.33 m
- Coeficiente estático, μs=0.5
- Coeficiente cinético, μk=0.9μs=0.45
Calculamos el ángulo para el cual la fuerza de rozamiento alcanza su valor máximo, resolviendo la ecuación transcendente con el comando
Representamos μs en función de la posición angular del cuerpo θ. Calculamos su valor máximo. Calculamos el ángulo θd para cual el cuerpo empieza a deslizar cuando μs=0.5 inferior al máximo μm=0.6216
w=7.5; %velocidad angular de rotación
R=0.33; %radio del cilindro
f=@(x) sin(x)./(cos(x)+w^2*R/9.8);
fplot(f,[0,pi])
th_m=acos(-9.8/(w^2*R));
line([th_m,th_m],[0,f(th_m)],'lineStyle','--', 'color','k')
line([0,th_m],[f(th_m),f(th_m)],'lineStyle','--', 'color','k')
mu_s=0.5; %coeficiente estático
g=@(x) f(x)-mu_s;
th_d=fzero(g,[0,th_m]);
line([0,th_d],[mu_s,mu_s], 'lineStyle','--','color','r')
line([th_d,th_d],[0,mu_s], 'lineStyle','--','color','r')
grid on
ylim([0,0.65])
set(gca,'XTick',0:pi/4:pi)
set(gca,'XTickLabel',{'0','\pi/4','\pi/2','3\pi/4','\pi'})
xlabel('\theta')
ylabel('\mu_s')
title('Coeficiente estático')
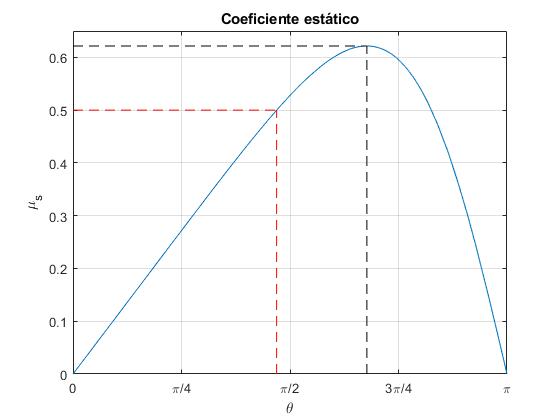
>> th_m*180/pi ans = 121.8668 >> f(th_m) ans = 0.6216 >> th_d*180/pi ans = 84.4607
La primera intersección de la línea horizontal μs=0.5 con la curva se produce para θd=1.4741 (84.5°). Prolongando esta línea, encontramos la otra posición angular del cuerpo en la que la fuerza de rozamiento alcanza su valor máximo es
>> fzero(g,[th_m,pi]) ans = 2.5948
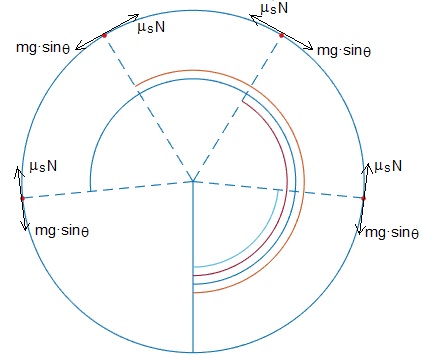
2.5948 (148.7°) y sus simétricas: 360-84.5=275.5° y 360-148.7=211.3°. En la figura, se muestra las cuatro posiciones, en cada posición se ha dibujado la componenente tangencial del peso y la fuerza de rozamiento, μsN máxima, justo cuando el cuerpo empueza a deslizar
w=7.5; %velocidad angular d erotación R=0.33; %radio del cilindro th_m=acos(-9.8/(w^2*R)); mu_s=0.5; %coeficiente estático g=@(x) sin(x)./(cos(x)+w^2*R/9.8)-mu_s; th_d1=fzero(g,[0,th_m])-pi/2; th_d2=fzero(g,[th_m,pi])-pi/2; hold on fplot(@(x) cos(x), @(x) sin(x),[0,2*pi]) plot(cos(th_d1),sin(th_d1),'ro','markersize',3,'markeredgecolor','r' ,'markerfacecolor','r') plot(cos(th_d2),sin(th_d2),'ro','markersize',3,'markeredgecolor','r', 'markerfacecolor','r') plot(-cos(th_d1),sin(th_d1),'ro','markersize',3,'markeredgecolor','r', 'markerfacecolor','r') plot(-cos(th_d2),sin(th_d2),'ro','markersize',3,'markeredgecolor','r', 'markerfacecolor','r') line([0,0],[0,-1]) fplot(@(x) 0.5*cos(x), @(x) 0.5*sin(x),[-pi/2,th_d1]) fplot(@(x) 0.55*cos(x), @(x) 0.55*sin(x),[-pi/2,th_d2]) fplot(@(x) 0.6*cos(x), @(x) 0.6*sin(x),[-pi/2,pi-th_d1]) fplot(@(x) 0.65*cos(x), @(x) 0.65*sin(x),[-pi/2,pi-th_d2]) line([0,cos(th_d1)], [0,sin(th_d1)],'lineStyle','--') line([0,cos(th_d2)], [0,sin(th_d2)],'lineStyle','--') line([0,-cos(th_d1)], [0,sin(th_d1)],'lineStyle','--') line([0,-cos(th_d2)], [0,sin(th_d2)],'lineStyle','--') hold off grid on axis off axis equal
El cuerpo desliza sobre la superficie cilíndrica
El cuerpo se encuentra en el instante td=θd/ω=0.1965, en la posición θd=1.4741 (84.5°) con velocidad angular dθ/dt=ω=7.5 rad/s y va a empezar a deslizar sobre la superficie cilíndrica. La ecuación del movimiento (véase la primera figura) es
Resolvemos esta ecuación diferencial por procedimientos numéricos, con las siguientes condiciones iniciales, en el instante td=θd/ω, la posición inicial del cuerpo es θd y su velocidad angular inicial es ω
La velocidad angular del cuerpo disminuye al principio (la componente tangencial del peso mgsinθ es mayor que la fuerza de rozamiento μkN), alcanza un valor mínimo y luego, crece hasta que se iguala al velocidad angular de rotación del cilindro (en reposo relativo)
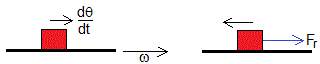
Como la velocidad del cuerpo dθ/dt<ω, el sentido de la fuerza de rozamiento es opuesto a la velocidad relativa del cuerpo respecto de la superficie cilíndrica en rotación
Definimos una función que detiene el proceso de integración por el procedimiento numérico
function [value,isterminal,direction]=stop_roza_cilindro(~,x, w)
value=x(2)-w;
isterminal=1;
direction=0; %crece o decrece
end
Elaboramos un script para representar la velocidad angular del cuerpo en función de su posición angular. Entre 0 y td la velocidad angular del cuerpo es constante e igual a ω (en reposo sobre la superficie cilíndrica)
w=7.5; %velocidad angular de rotación
R=0.33; %radio del cilindro
mu_s=0.5; %coeficiente estático, menor que el máximo
mu_k=0.9*mu_s; %coeficiente cinético
th_m=acos(-9.8/(w^2*R)); %ángulo del máximo
g=@(x) sin(x)./(cos(x)+w^2*R/9.8)-mu_s;
th_d=fzero(g,[0,th_m]);
td=th_d/w; %tiempo que tarda desde el origen hasta th_d
hold on
line([0,th_d],[w,w], 'color','r') %desde el origen hasta que empieza a deslizar
f=@(t,x) [x(2); -9.8*sin(x(1))/R+mu_k*(9.8*cos(x(1))/R+w^2)];
opts=odeset('events',@(t,x) stop_roza_cilindro(t,x,w));
[t,x]=ode45(f,[td,50],[th_d,w],opts);
plot(x(:,1), x(:,2))
hold off
grid on
xlabel('\theta')
ylabel('d\theta/dt')
title('Cuerpo que desliza en un cilindro que gira')
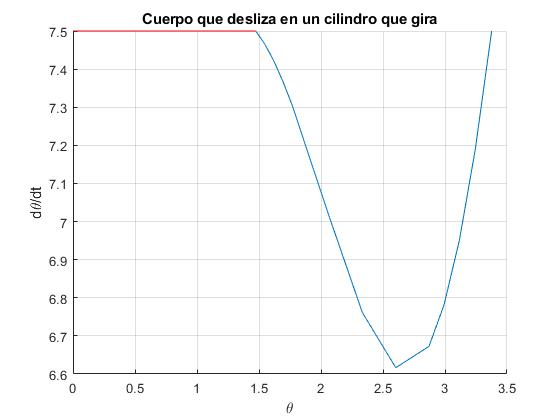
>> td td = 0.1965 >> th_d th_d = 1.4741 >> t(end) ans = 0.4698 >> x(end,1) ans = 3.3763 >> x(end,2) ans = 7.5000
El cuerpo se mantiene en reposo sobre la superficie cilíndrica hasta el instante td=0.1965, cuando su posición es θd=1.4741 (84.5°). Empieza a deslizar en esta posición, hasta que en el instante 0.4698, se iguala la velocidad del cuerpo dθ/dt con la velocidad angular del cilindro ω en la posición angular θ=3.3763 (193.4°)
El cuerpo en reposo
El cuerpo permenece en reposo relativo a la superficie del cilindro, desde la posición angular θ=3.3763 (193.4°) hasta que la fuerza de rozamiento alcanza su valor máximo en la posición, 3.6884 (211.3°) calculada en el primer apartado 'El cuerpo en reposo'. En esta posición, empieza a deslizar en el instante, td=0.4698+(3.6884-3.3763)/ω=0.5114 s.
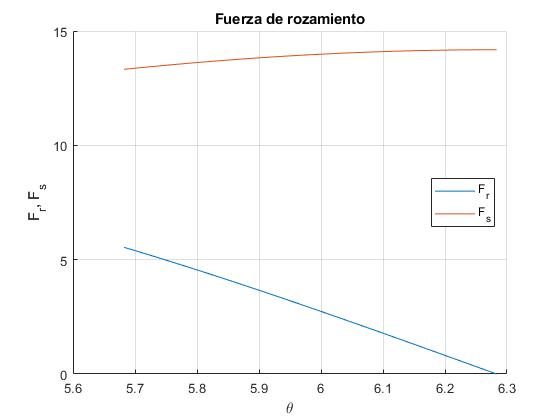
Comprobamos que la fuerza de rozamiento Fr=mgsinθ se mantiene inferior a la máxima μsN en el intervalo 3.3763 (193.4°)<θ<3.6884 (211.3°)
w=7.5; %velocidad angular de rotación
R=0.33; %radio del cilindro
mu_s=0.5; %coeficiente estático, menor que el máximo
hold on
fplot(@(x) abs(9.8*sin(x)),[3.3763,3.6884])
fplot(@(x) mu_s*(9.8*cos(x)+w^2*R),[3.3763,3.6884])
hold off
grid on
xlabel('\theta')
ylabel('F_r, F_s')
legend('F_r', 'F_s','location','best')
title('Fuerza de rozamiento')
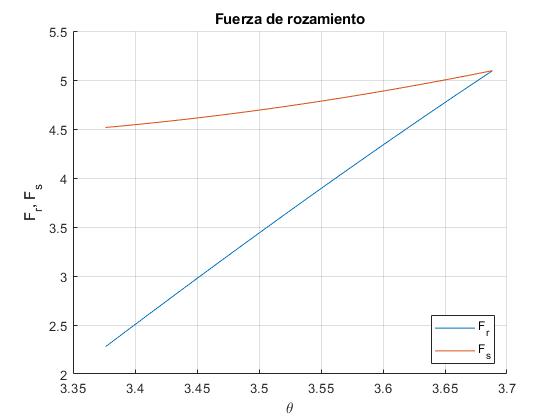
El cuerpo desliza sobre la superficie cilíndrica
El cuerpo se encuentra en el instante td=0.5114, en la posición 3.6884 (211.3°) con velocidad angular dθ/dt=ω=7.5 rad/s y va a empezar a deslizar sobre la superficie cilíndrica. La ecuación del movimiento es similar salvo el signo de la fuerza de rozamiento que ha cambiado de sentido
Como la velocidad del cuerpo dθ/dt>ω, el sentido de la fuerza de rozamiento es opuesto a la velocidad relativa del cuerpo respecto de la superficie cilíndrica en rotación
Resolvemos esta ecuación diferencial por procedimientos numéricos, con las siguientes condiciones iniciales, en el instante td, la posición inicial del cuerpo es θd y su velocidad angular inicial es ω
La velocidad angular del cuerpo aumenta al principio (la componente tangencial del peso mgsinθ es mayor que la fuerza de rozamiento μkN, alcanza un valor máximo y luego, disminuye hasta que se iguala al velocidad angular de rotación del cilindro (en reposo relativo)
Añadimos al script anterior las líneas de código que resuelven esta ecuación diferencial y para representar la velocidad angular del cuerpo en función de su posición angular.
w=7.5; %velocidad angular de rotación
R=0.33; %radio del cilindro
mu_s=0.5; %coeficiente estático, menor que el máximo
mu_k=0.9*mu_s; %coeficiente cinético
th_m=acos(-9.8/(w^2*R)); %ángulo del máximo
g=@(x) sin(x)./(cos(x)+w^2*R/9.8)-mu_s;
th_d1=fzero(g,[0,th_m]);
th_d2=fzero(g,[th_m,pi]);
td=th_d1/w; %tiempo que tarda desde el origen hasta th_d
hold on
line([0,th_d1],[w,w], 'color','r') %en reposo
f=@(t,x) [x(2); -9.8*sin(x(1))/R+mu_k*(9.8*cos(x(1))/R+w^2)];
opts=odeset('events',@(t,x) stop_roza_cilindro(t,x,w));
[t,x]=ode45(f,[td,50],[th_d1,w],opts);
plot(x(:,1), x(:,2),'b')
line([x(end,1),2*pi-th_d2],[w,w], 'color','r') %en reposo
td=t(end)+(2*pi-th_d2-x(end,1))/w;
f=@(t,x) [x(2); -9.8*sin(x(1))/R-mu_k*(9.8*cos(x(1))/R+w^2)];
opts=odeset('events',@(t,x) stop_roza_cilindro(t,x,w));
[t,x]=ode45(f,[td,5],[2*pi-th_d2,w],opts);
plot(x(:,1), x(:,2),'b')
hold off
grid on
xlabel('\theta')
ylabel('d\theta/dt')
title('Cuerpo que desliza en un cilindro que gira')
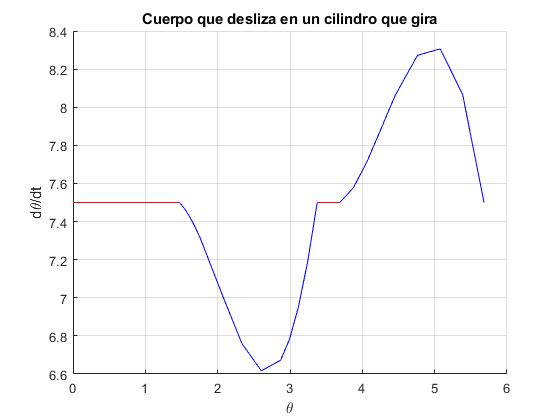
>> t(end) ans = 0.7615 >> x(end,1) ans = 5.6824 >> x(end,2) ans = 7.5000
El cuerpo empieza a deslizar en el instante 0.5114 s cuando su posición es 3.6884 (211.3°), hasta el instante 0.7615 s, en el que se iguala la velocidad del cuerpo dθ/dt con la velocidad angular del cilindro ω en la posición angular θ=5.6824 (325.6°)
El cuerpo en reposo
Comprobamos que la fuerza de rozamiento Fr=mgsinθ se mantiene inferior a la máxima μsN en el intervalo 5.6824 (325.6°)<θ<2π (360°), el cuerpo está en reposo relativo a la superficie cilíndrica. Regresa al origen en el instante 0.7615+(2π-5.6824)/ω=0.8416 s, que es el tiempo que tarda en dar una vuelta completa
w=7.5; %velocidad angular de rotación
R=0.33; %radio del cilindro
mu_s=0.5; %coeficiente estático, menor que el máximo
hold on
fplot(@(x) abs(9.8*sin(x)),[5.6824, 2*pi])
fplot(@(x) mu_s*(9.8*cos(x)+w^2*R),[5.6824, 2*pi])
hold off
grid on
xlabel('\theta')
ylabel('F_r, F_s')
legend('F_r', 'F_s','location','best')
title('Fuerza de rozamiento')
Resumen
Completamos el script anterior añadiendo el cuerpo en reposo en el intervalo 5.6824 (325.6°)<θ<2π (360°)
w=7.5; %velocidad angular de rotación
R=0.33; %radio del cilindro
mu_s=0.5; %coeficiente estático, menor que el máximo
mu_k=0.9*mu_s; %coeficiente cinético
th_m=acos(-9.8/(w^2*R)); %ángulo del máximo
g=@(x) sin(x)./(cos(x)+w^2*R/9.8)-mu_s;
th_d1=fzero(g,[0,th_m]);
th_d2=fzero(g,[th_m,pi]);
td=th_d1/w; %tiempo que tarda desde el origen hasta th_d
hold on
line([0,th_d1],[w,w], 'color','r') %en reposo
f=@(t,x) [x(2); -9.8*sin(x(1))/R+mu_k*(9.8*cos(x(1))/R+w^2)];
opts=odeset('events',@(t,x) stop_roza_cilindro(t,x,w));
[t,x]=ode45(f,[td,50],[th_d1,w],opts);
plot(x(:,1), x(:,2),'b')
line([x(end,1),2*pi-th_d2],[w,w], 'color','r') %en reposo
td=t(end)+(2*pi-th_d2-x(end,1))/w;
f=@(t,x) [x(2); -9.8*sin(x(1))/R-mu_k*(9.8*cos(x(1))/R+w^2)];
opts=odeset('events',@(t,x) stop_roza_cilindro(t,x,w));
[t,x]=ode45(f,[td,5],[2*pi-th_d2,w],opts);
plot(x(:,1), x(:,2),'b')
line([x(end,1),2*pi],[w,w], 'color','r') %en reposo
hold off
grid on
xlim([0,2*pi])
set(gca,'XTick',0:pi/4:2*pi)
set(gca,'XTickLabel',{'0','\pi/4','\pi/2','3\pi/4','\pi',
'5\pi/4', '3\pi/2','7\pi/4','2\pi'})
xlabel('\theta')
ylabel('d\theta/dt')
title('Cuerpo que desliza en un cilindro que gira')
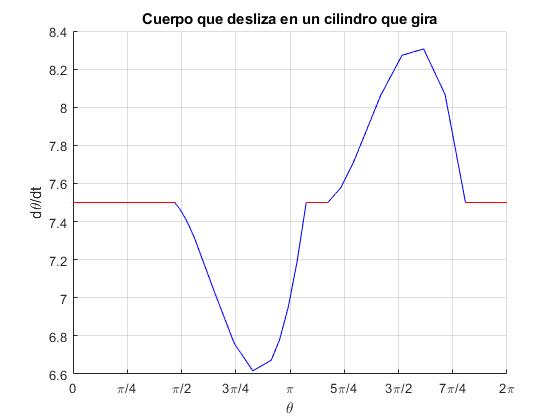
| Situación | Intervalo angular | Intervalo de tiempo |
|---|---|---|
| reposo | [0°,84.5°] | [0, 0.1965] |
| desliza | [84.5°, 193.4°] | [0.1965, 0.4698] |
| reposo | [193.4°, 211.3°] | [0.4698, 0.5114] |
| desliza | [211.3°, 325.6°] | [0.5114, 0.7615] |
| reposo | [325.6°, 360°] | [0.7615, 0.8416] |
Regresamos a la posición de partida.
Casos particulares
Cuando el coeficiente estático es superior al máximo μm=0.6216, el cuerpo permenece en reposo, relativo a la superficie cilíndrica
Cuando la superficie cilíndrica es lisa, sin rozamiento, el movimiento del cuerpo es similar al de un cuerpo que se mueve en un cúpula semiesférica cóncava, el cuerpo parte del origen θ=0, con velocidad angular ω. El principio de conservación de la energía nos permite calcular el máximo desplazamiento angular
Con los datos radio del cilindro R=0.33 m, velocidad angular de rotación, ω=7.5 rad/s, obtenemos el máximo desplazamiento angular θm=1.5178 (87.0°)
Actividades
Se introduce
- La velocidad angular constante de rotación del cilindro ω, en el control titulado Velocidad angular. La velocidad angular tiene que ser superior a la mínima 5.45 rad/s, para que el cuerpo no caiga, en caso contrario un mensaje nos lo advierte
- El coeficiente estático μs, en el control titulado Coef. estático
- El coeficiente cinético se ha fijado en μk=0.9μs
- El radio de la superficie cilíndrica se ha fijado en R=0.33 m
El cuerpo parte del origen θ=0 con velocidad angular ω (en reposo respecto de la superficie cilíndrica). Observaremos las distintas etapas de su movimiento
En la parte izquierda, se proporcionan los siguientes datos:
- El tiempo t
- El ángulo girado por la superficie cilíndrica, φ=ωt
- La posición angular del cuerpo, θ en grados
- La velocidad angular de rotación del cilindro ω
- La velocidad angular del cuerpo, dθ/dt
- El valor absoluto de la componente tangencial del peso, mgsinθ
- El valor máximo de la fuerza de rozamiento μsN
- El estado del cuerpo: en reposo o deslizando sobre la superficie cilíndrica
La componente tangencial del peso, se representa mediante una flecha de color azul. La fuerza de rozamiento, se representa mediante una flecha de color rojo
Referencias
Brian D. Harper. Solving Dynamics Problems in Maple. JOHN WILEY & SONS, INC. 3.6 Problem 3/365 (Curvilinear Motion), pág. 66

