En la página titulada Trabajo, energía cinética y energía potencial, vimos que la fuerza que ejerce un muelle elástico sobre una partícula, F=-kx es conservativa y la energía potencial es kx²/2, tomando como nivel cero de energía potencial cuando el muelle está sin deformar, x=0

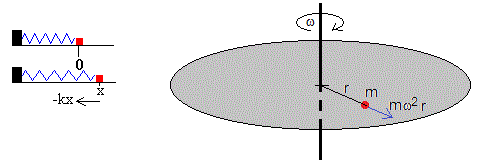
Cuando una partícula de masa m está situada a una distancia r del eje de rotación de una plataforma que gira con velocidad angular constante ω, experimenta una fuerza centrífuga mω²r. Esta fuerza es conservativa y su energía potencial es -mω²r²/2, tomando como nivel cero de energía potencial cuando la partícula está en el eje r=0.

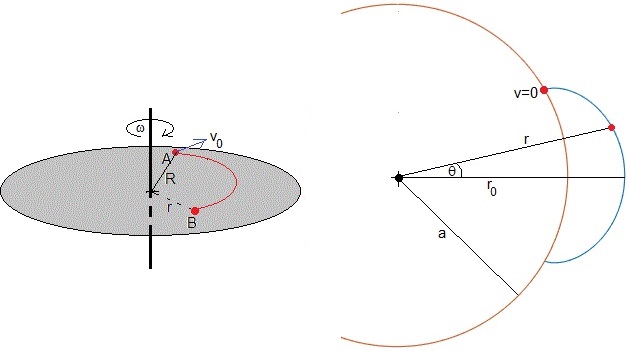
Supongamos que disponemos de una plataforma en rotación de radio muy grande. Se lanza una partícula de masa m con velocidad inicial v₀ cuando se encuentra a una distancia R del eje de rotación. Si no hay rozamiento, cuando se encuentre a una distancia r de eje de rotación su velocidad será v. Aplicando el principio de conservación de la energía

${\displaystyle \begin{array}{l}\frac{1}{2}m{v}^2-\frac{1}{2}m{\omega }^2{r}^2=\frac{1}{2}m{v}_0^2-\frac{1}{2}m{\omega }^2{R}^2\\ v=\sqrt{{\omega }^2{r}^2+v_0^2-{\omega }^2{R}^2}=\omega \sqrt{r^2-\left(R^2-\frac{v_0^2}{{\omega }^2}\right)}=\omega \sqrt{r^2-a^2}\end{array}}$

Denominamos a a la distancia al eje para la cual la velocidad v de la partícula se hace cero

Ecuación de la trayectoria

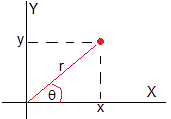
Expresamos el arco $ds=\sqrt{d{x}^2+d{y}^2}$, en coordenadas polares

x=rcosθ, y=rsinθ

dx=dr·cosθ-rsinθ·dθ, dy=dr·sinθ+rcosθ·dθ

${\displaystyle ds=\sqrt{d{r}^2+r^{2}d{\theta }^2}=\sqrt{{\left(\frac{dr}{d\theta }\right)}^2+r^2}·d\theta =\sqrt{{\dot{r}}^2+r^2}·d\theta }$

El tiempo t que tarda en desplazarse una partícula entre A y B es

${\displaystyle t=\underset{A}{\overset{B}{{\displaystyle \int }}}\frac{ds}{v}=\underset{A}{\overset{B}{{\displaystyle \int }}}\frac{\sqrt{{\dot{r}}^2+r^2}}{\omega \sqrt{r^2-a^2}}d\theta }$

Tenemos que buscar la función r=r(θ) que haga la funcional t(r) extremo. Dado que el integrando, la función

${\displaystyle f(\theta ,r,\dot{r})=\frac{\sqrt{{\dot{r}}^2+r^2}}{\sqrt{r^2-a^2}}}$

no depende de θ, la ecuación de Euler-Lagrange se escribe

${\displaystyle \begin{array}{l}f-\dot{r}\frac{\partial f}{\partial \dot{r}}=C_1\hfill \\ \frac{r^2}{\sqrt{r^2-a^2}\sqrt{{\dot{r}}^2+r^2}}=C_1\hfill \end{array}}$

C₁ es una constante que se evalúa para el máximo r₀ de la trayectoria r=r(θ), es decir, cuando dr/dθ=0. Véase la figura más arriba

${\displaystyle r_0=\frac{C_1}{\sqrt{C_1^2-1}}a}$

En términos del nuevo parámetro r₀, la ecuación diferencial de la trayectoria se escribe

${\displaystyle \begin{array}{l}\frac{r^2}{\sqrt{r^2-a^2}\sqrt{{\dot{r}}^2+r^2}}=\frac{r_0}{\sqrt{r_0^2-a^2}}\hfill \\ \frac{dr}{d\theta }=-r\frac{a}{r_0}\sqrt{\frac{r_0^2-r^2}{r^2-a^2}}\hfill \\ \frac{a}{r_0}\theta =-{{\displaystyle \int }}^{\text{}}\sqrt{\frac{r^2-a^2}{r_0^2-r^2}}\frac{dr}{r}+C_2\hfill \end{array}}$

Para la fuerza de atracción F<0 se ha tomado el signo positivo de la raíz cuadrada, para una fuerza F>0 (centrífuga) se toma el signo negativo.

La ecuación de la trayectoria es casi idéntica a la estudiada en la página El viaje más rápido a través de un túnel por el interior de la Tierra, difieren en el signo y en el nombre del parámetro R (radio de la esfera) que se ha cambiado por a, relacionado con la posición inicial y la velocidad inicial. La partícula se encuentra en reposo, tanto a la distancia R como a la distancia a

Siguiendo los mismos pasos, resolvemos la integral del segundo miembro, haciendo el cambio

${\displaystyle \begin{array}{l}u=\sqrt{\frac{r_0^2-r^2}{r^2-a^2}}r=\sqrt{\frac{r_0^2+a^2{u}^2}{1+u^2}}\hfill \\ dr=\frac{u}{r}\frac{a^2-r_0^2}{{(1+u^2)}^2}du\hfill \end{array}}$

El resultado de la integral es

${\displaystyle \begin{array}{l}{{\displaystyle \int }}^{\text{}}\sqrt{\frac{r^2-a^2}{r_0^2-r^2}}\frac{dr}{r}={{\displaystyle \int }}^{\text{}}\frac{1}{r^2}\frac{a^2-r_0^2}{{(1+u^2)}^2}du={{\displaystyle \int }}^{\text{}}\frac{(a^2-r_0^2)du}{(r_0^2+a^2{u}^2)(1+u^2)}=\hfill \\ {{\displaystyle \int }}^{\text{}}\frac{(a^2+a^2{u}^2-a^2{u}^2-r_0^2)du}{(r_0^2+a^2{u}^2)(1+u^2)}=a^2{{\displaystyle \int }}^{\text{}}\frac{du}{r_0^2+a^2{u}^2}-{{\displaystyle \int }}^{\text{}}\frac{du}{1+u^2}=\hfill \\ \frac{a}{r_0}{\tan }^{-1}\left(\frac{a}{r_0}u\right)-{\tan }^{-1}u=\frac{a}{r_0}{\tan }^{-1}\left(\frac{a}{r_0}\sqrt{\frac{r_0^2-r^2}{r^2-a^2}}\right)-{\tan }^{-1}\left(\sqrt{\frac{r_0^2-r^2}{r^2-a^2}}\right)\hfill \end{array}}$

La ecuación implícita de la trayectoria, r=r(θ), es

${\displaystyle \theta =-{\tan }^{-1}\left(\frac{a}{r_0}\sqrt{\frac{r_0^2-r^2}{r^2-a^2}}\right)+\frac{r_0}{a}{\tan }^{-1}\left(\sqrt{\frac{r_0^2-r^2}{r^2-a^2}}\right)+C_2}$

Donde θ se mide desde el eje de simetría. Véase la figura al principio de la página

Para r=r₀, cuando r es máximo, θ=0, por lo que C₂=0. Para r=a, cuando la velocidad de la partícula se hace cero

${\displaystyle \theta =-\frac{\pi }{2}+\frac{r_0}{a}\frac{\pi }{2}=\frac{\pi }{2}\left(\frac{r_0}{a}-1\right)}$

El ángulo subtendido por la trayectoria, entre las posiciones inicial y final, por simetría, es el doble

${\displaystyle \Delta \theta =\pi \left(\frac{r_0}{a}-1\right)}$

Tiempo que tarda en recorrer el camino

Teniendo en cuenta que

${\displaystyle \dot{r}=\frac{dr}{d\theta }=-r\frac{a}{r_0}\sqrt{\frac{r_0^2-r^2}{r^2-a^2}}}$

Calculamos la expresión del tiempo t

${\displaystyle \begin{array}{l}t=\underset{A}{\overset{B}{{\displaystyle \int }}}\frac{\sqrt{{\left(\frac{dr}{d\theta }\right)}^2+r^2}}{\omega \sqrt{r^2-a^2}}d\theta =-\frac{\sqrt{r_0^2-a^2}}{a\omega }{\displaystyle \underset{A}{\overset{B}{\int }}\frac{r·dr}{\sqrt{r_0^2-r^2}\sqrt{r^2-a^2}}}=\\ -\frac{\sqrt{r_0^2-a^2}}{a\omega }{\displaystyle \underset{A}{\overset{B}{\int }}\frac{r·dr}{\sqrt{{\left(\frac{a^2-r_0^2}{2}\right)}^2-{\left(\frac{a^2+r_0^2}{2}-r^2\right)}^2}}}\end{array}}$

Haciendo el cambio de variable

${\displaystyle \begin{array}{l}u=\frac{\frac{a^2+r_0^2}{2}-r^2}{\frac{a^2-r_0^2}{2}}=\frac{a^2+r_0^2-2r^2}{a^2-r_0^2}du=-\frac{4r·dr}{a^2-r_0^2}\\ \frac{\sqrt{r_0^2-a^2}}{a\omega }\frac{1}{2}{{\displaystyle \underset{A}{\overset{B}{\int }}\frac{du}{\sqrt{1-u^2}}=\frac{\sqrt{r_0^2-a^2}}{a\omega }\frac{1}{2}{\sin }^{-1}\left(\frac{a^2+r_0^2-2r^2}{a^2-r_0^2}\right)|}}_A^B\end{array}}$

Tomando tiempo t=0, cuando la trayectoria pasa por el máximo r=r₀

${\displaystyle \begin{array}{l}t={\frac{\sqrt{r_0^2-a^2}}{a\omega }\frac{1}{2}{\sin }^{-1}\left(\frac{a^2+r_0^2-2r^2}{a^2-r_0^2}\right)|}_{r_0}^r\\ t=\frac{\sqrt{r_0^2-a^2}}{a\omega }\frac{1}{2}\left({\sin }^{-1}\left(\frac{a^2+r_0^2-2r^2}{a^2-r_0^2}\right)-{\sin }^{-1}1\right)=\frac{\sqrt{r_0^2-a^2}}{a\omega }\frac{1}{2}\left({\sin }^{-1}\left(\frac{a^2+r_0^2-2r^2}{a^2-r_0^2}\right)-\frac{\pi }{2}\right)\end{array}}$

Finalmente, por simetría, el tiempo de viaje T es el doble del tiempo que tarda en ir del máximo r₀ a a

${\displaystyle \begin{array}{l}T={2\frac{1}{2}\frac{\sqrt{r_0^2-a^2}}{a\omega }\left({\sin }^{-1}\left(\frac{a^2+r_0^2-2r^2}{a^2-r_0^2}-\frac{\pi }{2}\right)\right)|}_{r_0}^a\hfill \\ T=\frac{\sqrt{r_0^2-a^2}}{a\omega }\left(\frac{3}{2}\pi -\frac{\pi }{2}\right)=\pi \frac{\sqrt{r_0^2-a^2}}{a\omega }\hfill \end{array}}$

Ecuaciones paraméricas de la trayectoria

Llamando Ω=π/T, en la ecuación que nos da el tiempo t, despejamos r²

${\displaystyle \begin{array}{l}t=\frac{\sqrt{r_0^2-a^2}}{a\omega }\frac{1}{2}\left({\sin }^{-1}\left(\frac{a^2+r_0^2-2r^2}{a^2-r_0^2}\right)-\frac{\pi }{2}\right)\\ \sin \left(2\Omega t+\frac{\pi }{2}\right)=\frac{a^2+r_0^2-2r^2}{a^2-r_0^2}\\ r^2=\frac{a^2+r_0^2}{2}+\frac{r_0^2-a^2}{2}\cos \left(2\Omega t\right)\end{array}}$

Expresamos la posición angular θ en función del tiempo t. El cociente

${\displaystyle \frac{r_0^2-r^2}{r^2-a^2}=\frac{1-\cos \left(2\Omega t\right)}{1+\cos \left(2\Omega t\right)}=\frac{2{\sin }^2\left(\Omega t\right)}{2{\cos }^2\left(\Omega t\right)}={\tan }^2\left(\Omega t\right)}$

El resultado es

${\displaystyle \begin{array}{l}\theta =-{\tan }^{-1}\left(\frac{a}{r_0}\sqrt{\frac{r_0^2-r^2}{r^2-a^2}}\right)+\frac{r_0}{a}{\tan }^{-1}\left(\sqrt{\frac{r_0^2-r^2}{r^2-a^2}}\right)\\ \theta =-{\tan }^{-1}\left(\frac{a}{r_0}\tan \left(\Omega t\right)\right)+\frac{r_0}{a}\Omega t\end{array}}$

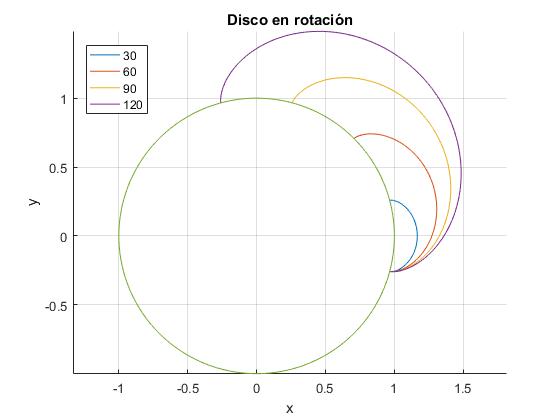
Conocidos r y θ en función del tiempo t dibujamos la trayectoria. Hacemos que la partícula parta de la misma posición. Las posiciones finales distan, 30, 60, 90, 120°

a=1;
w=1;
hold on
delta=0;
for ang=(30:30:120)*pi/180
    r0=(1+ang/pi)*a;
    T=pi*sqrt(r0^2-a^2)/(a*w);
    r2=@(t) (a^2+r0^2)/2+(r0^2-a^2)*cos(2*pi*t/T)/2;
    th=@(t) -atan(a*tan(pi*t/T)/r0)+r0*pi*t/(T*a);
    x=@(t) sqrt(r2(t)).*cos(th(t)+delta);
    y=@(t) sqrt(r2(t)).*sin(th(t)+delta);
    fplot(x,y,[-T/2,T/2], 'displayName',num2str(ang*180/pi))
    delta=ang/2;
end
legend('-DynamicLegend','location','northwest')
fplot(@(t) a*cos(t),@(t) a*sin(t),[0,2*pi])
hold off
axis equal
grid on
xlabel('x');
ylabel('y')
title('Disco en rotación')

Curvas cicloidales

La trayectoria es un arco de una curva denominada epitrocoide

${\displaystyle \{\begin{array}{l}x=\frac{a}{n}\left\{\left(n+1\right)\cos \phi -\cos \left((n+1)\phi \right)\right\}\\ y=\frac{a}{n}\left\{\left(n+1\right)\sin \phi +\sin \left((n+1)\phi \right)\right\}\end{array}}$

a=1;
n=5;
x=@(t) a*((n+1)*cos(t)-cos((n+1)*t))/n;
y=@(t) a*((n+1)*sin(t)-sin((n+1)*t))/n;
hold on
fplot(x,y,[0,2*pi])
fplot(@(t) a*cos(t),@(t) a*sin(t),[0,2*pi])
grid on
axis equal
xlabel('x')
ylabel('y')
title('Epitrocoide')

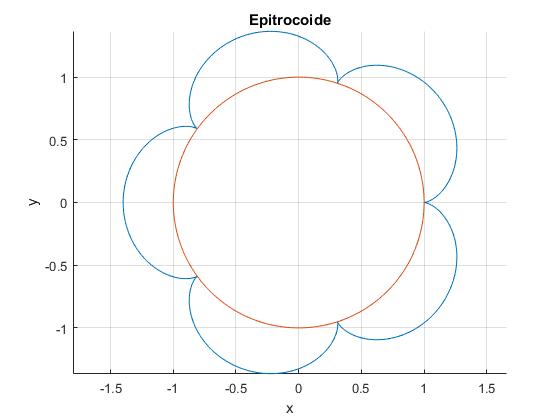
Se sugiere al lector cambiar el valor de n por ejemplo 2,3,4 (número entero), 5/3, 7/3, 8/3, 9/4 (número racional), π $\sqrt{2}$, véase la página Hypocycloid

En el programa interactivo de la página titulada Curvas cicloidales se generan curvas denominadas epicicloidales. Se trata de curvas engendradas por un punto ligado a una círculo móvil que rueda sin deslizar sobre una circunferencia fija. Cuando el círculo móvil es exterior a la circunfereencia fija, la curva engendrada recibe el nombre de epicicloide.

Referencias

John M. McKinley. Brachistochrones, tautochrones, evolutes and tesselations. Am. J. Phys. 47(1) January 1979, pp. 81-86