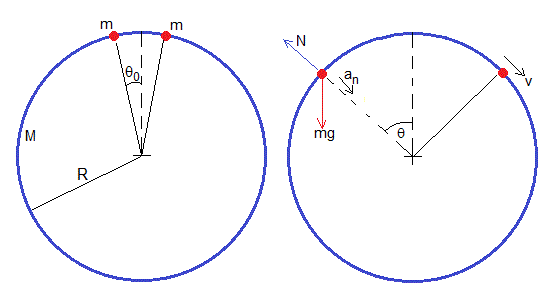
Dos partículas deslizan sin rozamiento a lo largo de un anillo en posición vertical
Un anillo de masa M y radio R permanece en posición vertical. Dos partículas iguales de masa m pueden deslizar sin rozamiento a lo largo del anillo, partiendo desde la posición inicial θ0 en reposo.
Supondremos que el anillo cuelga de una balanza. Vamos a calcular la fuerza T que mide en función de la posición angular θ de las partículas
Conservación de la energía
Cuando las partículas están en la posición θ, su velocidad es v.
Aplicamos el principio de conservación de la energía a cada una de las partículas, tomando el nivel cero de energía potencial en la parte inferior del anillo, θ=π
Dinámica del movimiento circular
Las fuerzas sobre cada una de las partículas son
- El peso, mg
- La fuerza N que ejerce el anillo sobre la partícula
Aplicando la dinámica del movimiento circular
La reacción N se hace cero para el ángulo θ
Si la posición inicial θ0=0, entonces, cosθ=2/3
Véase la página titulada Movimiento sobre una cúpula semiesférica para un caso similar
Fuerza sobre el anillo
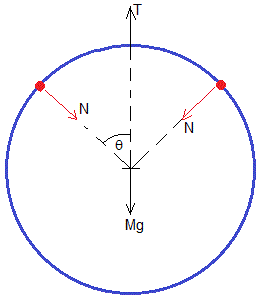
La fuerza T que ejerce el soporte que sujeta el anillo en posición vertical es
La fuerza T se anula para dos ángulos
Para que existan raíces reales, el discriminante tiene que ser positivo
Además, la resultante T presenta un mínimo para el ángulo θm
Ejemplo 1
Representamos la fuerza T en función del ángulo θ con los siguientes datos
- Radio del anillo, R=1 m
- Masa de las partículas, m=1 kg
- Masa del anillo, M=0.3 kg
- Posición inicial de las partículas, θ0= 5°
R=1; %radio anillo
th_0=5*pi/180; %angulo inicial
m=1; %masa partícula
M=0.3; %masa anillo
T=@(x) 2*m*9.8*(3*cos(x)-2*cos(th_0)).*cos(x)+M*9.8;
hold on
fplot(T,[th_0, pi])
if M/m<2*cos(th_0)^2/3
th_1=acos(cos(th_0)/3+sqrt(cos(th_0)^2/9-M/(6*m)));
th_2=acos(cos(th_0)/3-sqrt(cos(th_0)^2/9-M/(6*m)));
line([th_1, th_1],[0,-20], 'lineStyle','--')
line([th_2, th_2],[0,-20], 'lineStyle','--')
end
th_m=acos(cos(th_0)/3);
plot(th_m,T(th_m),'ro','markersize',3,'markerfacecolor','r')
line([0,pi],[M*9.8,M*9.8], 'color','r')
hold off
grid on
set(gca,'XTick',0:pi/6:pi)
set(gca,'XTickLabel',{'0','\pi/6','\pi/3','\pi/2','2\pi/3', '5\pi/6','\pi'})
xlabel('\theta')
ylabel('Fuerza (N)')
title('Fuerza sobre el anillo')
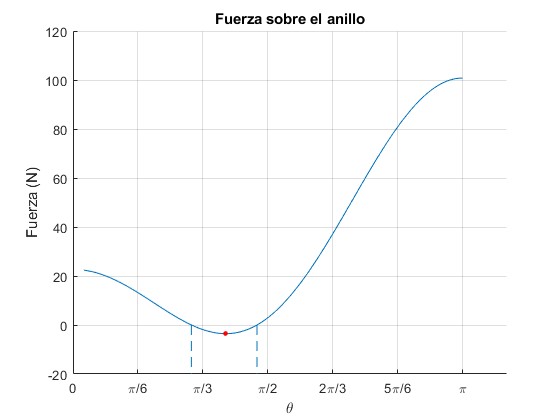
El discriminante de la ecuación de segundo grado en cosθ es positivo, hay dos ángulos θ1=54.7° y θ2=85.0° para los cuales la fuerza T se anula
>> [th_1,th_2]*180/pi ans = 54.7210 85.0336
Un punto de color rojo, señala el mínimo de la resultante T
La línea horizontal, señala el peso del aro. La fuerza T=Mg en dos posiciones: cuando N=0, para el ángulo cosθ=2cosθ0/3, y cuando θ=π/2, N es horizontal, su componente vertical es nula
>> th=acos(2*cos(th_0)/3); >> T(th)-M*9.8 ans = 0 >> T(pi/2)-M*9.8 ans = -2.2204e-15
Si cambiamos la masa M=2 kg del anillo, la fuerza T no se anula
Actividades
Se introduce
- La masa M del anillo en el control titulado Masa anillo
- El radio del anillo se ha fijado en R=1 m
- La masa de las partículas se ha fijado en, m=1 kg
- La posición inicial de las partículas, se ha fijado en θ0= 5°
Se pulsa el botón titulado Nuevo
Observamos las fuerzas sobre el anillo
- El peso Mg de anillo
- Las fuerzas N que ejercen las dos partículas sobre el anillo
En la parte superior izquierda, se proporcionan los datos de la posición de las partículas θ y de la fuerza resultante T
Movimiento de la partícula a lo largo del anillo
Analizamos el movimiento de la partícula a lo largo de la dirección tangencial, desde la posición inicial θ0 a la final θ=π.
La fuerza que actúa sobre la partícula es la componente mgsinθ del peso. La ecuación del movimiento es
Solución numérica
Se resuelve, mediante el procedimiento
Las condiciones iniciales son, en el instante t=0, θ=θ0, dθ/dt=0, parte del resposo
Solución analítica
La energía de la partícula en la posición inicial es
La energía de la partícula en la posición θ, es
A partir del principio de conservación de la energía, obtenemos la relación implícita entre la posición angular θ y el tiempo t
hemos utilizado la relación trigonométrica,
Integrando
Efectuamos el cambio de variable
El resultado es, véase la página titulada Integrales elípticas
El tiempo que tarda la partícula en desplazarse desde la posición inicial θ=θ0 a la final θ=π es
Comparamos las dos soluciones
function anillo_10
R=1; %radio
th_0=5*pi/180; %angulo inicial
k=cos(th_0/2);
tt=sqrt(1/9.8)*ellipke(k^2); %tiempo total
disp(tt)
xx=linspace(th_0,pi,100);
t=zeros(1,length(xx));
i=1;
for x=xx
t(i)=sqrt(R/9.8)*(ellipke(k^2)-ellipticF(asin(cos(x/2)/cos(th_0/2)),k^2));
i=i+1;
end
hold on
plot(t,xx)
%numérica
f=@(t,x) [x(2);9.8*sin(x(1))/R];
opts=odeset('events',@(t,x) stop_cupula(t,x));
[t,x]=ode45(f,[0,50],[th_0,0],opts);
plot(t,x(:,1))
disp(t(end)) %tiempo total
hold off
grid on
set(gca,'YTick',0:pi/6:pi)
set(gca,'YTickLabel',{'0','\pi/6','\pi/3','\pi/2','2\pi/3', '5\pi/6','\pi'})
legend('analítica','numérica','location','best')
xlabel('t')
ylabel('\theta')
title('Posición')
function [value,isterminal,direction]=stop_cupula(~,x)
value=x(1)-pi;
isterminal=1;
direction=1;
end
end
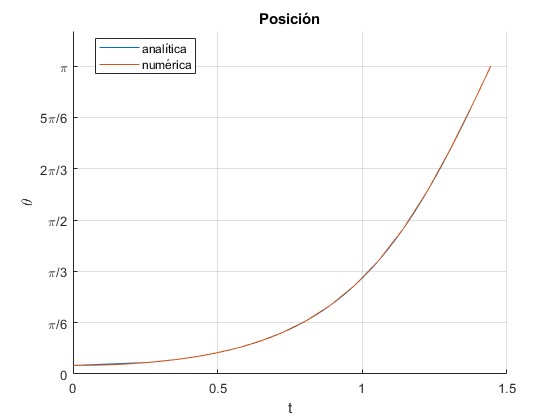
Ambas soluciones casi coinciden. Los tiempos de viaje calculados son
1.4439
1.4438
Las partículas tardan un tiempo tf=1.44 s en alcanzar la posición más baja, θ=π (180°), partiendo de la posición θ0=5°, en reposo.
Caso general
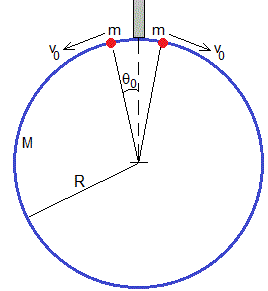
Un anillo de masa M y radio R permanece en posición vertical. Dos partículas iguales de masa m pueden deslizar sin rozamiento a lo largo del anillo, partiendo desde la posición inicial θ0 con velocidad v0.
Supondremos que el anillo cuelga de una balanza. Vamos a calcular la fuerza T que mide en función de la posición angular θ de las partículas
Cuando las partículas están en la posición θ, su velocidad es v.
Aplicamos el principio de conservación de la energía a cada una de las partículas, tomando el nivel cero de energía potencial en la parte inferior del anillo, θ=π
Las fuerzas sobre cada una de las partículas son
- El peso, mg
- La fuerza N que ejerce el anillo sobre la partícula
Aplicando la dinámica del movimiento circular
La reacción N se hace cero para el ángulo θ
Fuerza sobre el anillo
La fuerza T que ejerce el soporte que sujeta el anillo en posición vertical es
La fuerza T se anula para dos ángulos
Para que existan raíces reales, el discriminante tiene que ser positivo
Además, la resultante T presenta un mínimo para el ángulo θm
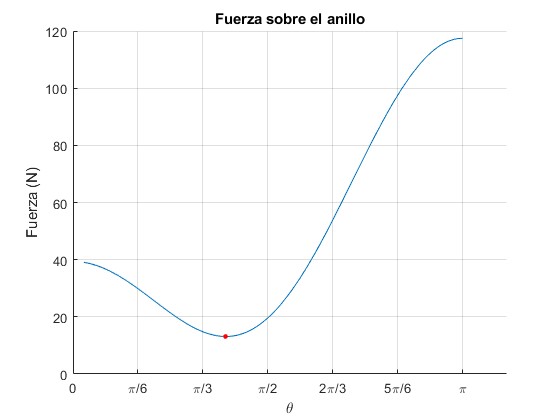
Ejemplo 1
Representamos la fuerza T en función del ángulo θ con los siguientes datos
- Radio del anillo, R=1 m
- Masa de las partículas, m=1 kg
- Masa del anillo, M=0.3 kg
- Posición inicial de las partículas, θ0= 5°
- Velocidad inicial de las partículas, v0= 1 m/s
R=1; %radio anillo
th_0=5*pi/180; %angulo inicial
v0=1; %velocidad inicial
m=1; %masa partícula
M=0.3; %masa anillo
T=@(x) 2*(m*9.8*(3*cos(x)-2*cos(th_0))-m*v0^2/R).*cos(x)+M*9.8;
hold on
fplot(T,[th_0, pi])
mu=cos(th_0)+v0^2/(2*9.8*R);
if M/m<2*mu^2/3
th_1=acos(mu/3+sqrt(mu^2/9-M/(6*m)));
th_2=acos(mu/3-sqrt(mu^2/9-M/(6*m)));
line([th_1, th_1],[0,-20], 'lineStyle','--')
line([th_2, th_2],[0,-20], 'lineStyle','--')
end
th_m=acos(cos(th_0)/3+v0^2/(2*9.8*R));
plot(th_m,T(th_m),'ro','markersize',3,'markerfacecolor','r')
hold off
grid on
set(gca,'XTick',0:pi/6:pi)
set(gca,'XTickLabel',{'0','\pi/6','\pi/3','\pi/2','2\pi/3', '5\pi/6','\pi'})
xlabel('\theta')
ylabel('Fuerza (N)')
title('Fuerza sobre el anillo')
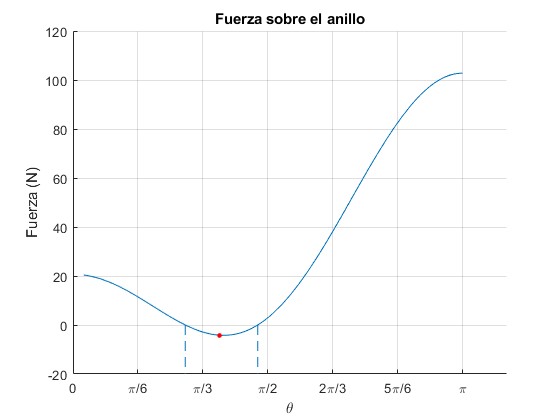
El discriminante de la ecuación de segundo grado en cosθ es positivo, hay dos ángulos θ1=51.9° y θ2=85.3° para los cuales la fuerza T se anula
>> [th_1,th_2]*180/pi ans = 51.8937 85.3527
Referencias
J Martínez-Torregrosa, P Sarriugarte, S Rosa-Cintas, J Guisasola. A circular motion problem to encourage deep understanding and use of scientific practices. Phys. Educ. 60 (2025) 045032
Marcella Kitzinger, João Octávio Oliveira-Cony, Gabriel Messias, Paulo Roberto Linhares, Carlos Farina de Souza. O problema do aro pulante e suas variações. Revista Brasileira de Ensino de Física, vol. 47, e20250432 (2025)

