El caso más simple, se da cuando la partícula está en reposo sobre la plataforma

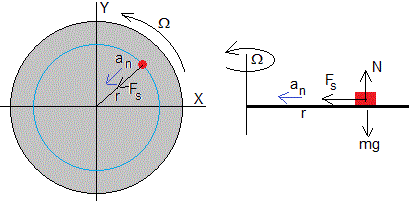
Cuando una partícula está en reposo sobre la plataforma en movimiento de rotación con velocidad angular constante Ω, la fuerza de rozamiento varía de 0 a su máximo valor μ_s·N=μ_s·mg, dependiendo de la distancia r de la partícula al origen.

Si una partícula describe una trayectoria circular de radio r, la fuerza de rozamiento que ejerce la plataforma sobre la partícula F_s, se obtiene aplicando la ecuación de la dinámica del movimiento circular uniforme

${\displaystyle m{\Omega }^{2}r=F_s}$

Sea R el radio para el cual la fuerza de rozamiento F_s adquiere su valor máximo μ_s·N=μ_s·mg. μ_s es el coeficiente estático

${\displaystyle \begin{array}{l}m{\Omega }^{2}R={\mu }_{s}mg\\ R=\frac{{\mu }_{s}g}{{\Omega }^2}\end{array}}$

R es la máxima distancia radial a la que puede estar la partícula sobre la plataforma en rotación, más allá de la cual no puede seguir en reposo. En otras palabras

• Si la partícula está en reposo dentro de la circunferencia de radio r<R, contuará en reposo
• Cuando se sitúa fuera de la circunferencia, r>R continúa deslizando hacia afuera
• Cuando se sitúa en la circunferencia, r=R estará en equilibrio inestable, cualquier perturbación le hará deslizar hacia fuera

Sistema de Referencia no inercial

El eje Z coincide con el eje de la plataforma $\overrightarrow{\Omega }=\Omega \widehat{k}$

Las fuerzas sobre la partícula serán

• La fuerza de rozamiento, de sentido contrario a la velocidad de la partícula

${\displaystyle {\overrightarrow{F}}_r=-{\mu }_{k}mg\frac{\overrightarrow{v}}{v}}$

μ_k es el coeficiente cinético

• La fuerza centrífuga

${\displaystyle {\overrightarrow{F}}_c=-m\overrightarrow{\Omega }\left(\overrightarrow{\Omega }\times \overrightarrow{r}\right)=m{\Omega }^2\overrightarrow{r}}$

• La fuerza de Coriolis

${\displaystyle {\overrightarrow{F}}_{co}=-2m\overrightarrow{\Omega }\times \overrightarrow{v}}$

La ecuación del movimiento es

${\displaystyle m\frac{d\overrightarrow{v}}{dt}=m{\Omega }^2\overrightarrow{r}-{\mu }_{k}mg\frac{\overrightarrow{v}}{v}-2m\overrightarrow{\Omega }\times \overrightarrow{v}}$

La posición, velocidad y aceleración de una partícula respecto de un observador situado en el centro de la plataforma

${\displaystyle \{\begin{array}{l}\overrightarrow{r}=x\widehat{i}+y\widehat{j}\\ \overrightarrow{v}=\frac{dx}{dt}\widehat{i}+\frac{dy}{dt}\\ \frac{d\overrightarrow{v}}{dt}=\frac{d^{2}x}{d{t}^2}\widehat{i}+\frac{d^{2}y}{d{t}^2}\end{array}}$

Tenemos que resolver el sistema de dos ecuaciones diferenciales

${\displaystyle \{\begin{array}{l}\frac{d^{2}x}{d{t}^2}={\Omega }^{2}x-\frac{{\mu }_{k}g}{\sqrt{{\left(\frac{dx}{dt}\right)}^2}+{\left(\frac{dy}{dt}\right)}^2}\frac{dx}{dt}+2\Omega \frac{dy}{dt}\\ \frac{d^{2}y}{d{t}^2}={\Omega }^{2}y-\frac{{\mu }_{k}g}{\sqrt{{\left(\frac{dx}{dt}\right)}^2}+{\left(\frac{dy}{dt}\right)}^2}\frac{dy}{dt}-2\Omega \frac{dx}{dt}\end{array}}$

Caso particular, cuando no hay rozamiento

${\displaystyle \{\begin{array}{l}\frac{d^{2}x}{d{t}^2}-2\Omega \frac{dy}{dt}-{\Omega }^{2}x=0\\ \frac{d^{2}y}{d{t}^2}+2\Omega \frac{dx}{dt}-{\Omega }^{2}y=0\end{array}}$

Utilizamos la notación compleja

${\displaystyle \begin{array}{l}\xi =x+iy\\ \frac{d^2\xi }{d{t}^2}-2\Omega \left(\frac{dy}{dt}-i\frac{dx}{dt}\right)-{\Omega }^2\xi =0\\ \frac{d^2\xi }{d{t}^2}+2\Omega i\left(\frac{dx}{dt}+i\frac{dy}{dt}\right)-{\Omega }^2\xi =0\\ \frac{d^2\xi }{d{t}^2}+2\Omega i\frac{d\xi }{dt}-{\Omega }^2\xi =0\end{array}}$

Las raíces de la ecuación característica son

${\displaystyle s^2+2\Omega is-{\Omega }^2={\left(s+i\Omega \right)}^2=\mathrm{0,}\{\begin{array}{l}{s}_1=-i\Omega \\ s_2=-i\Omega \end{array}}$

La solución de esta ecuación diferencial lineal con raíces repetidas es

${\displaystyle \begin{array}{l}\xi =C\exp \left(-i\Omega t\right)+Dt\exp \left(-i\Omega t\right)\\ \frac{d\xi }{dt}=-i\Omega C\exp \left(-i\Omega t\right)+D\exp \left(-i\Omega t\right)-i\Omega Dt\exp \left(-i\Omega t\right)\end{array}}$

Donde C y D son números complejos cuya parte real e imaginaria se determinan a partir de las condiciones iniciales:

${\displaystyle t=0\{\begin{array}{l}\frac{dx}{dt}=v_{0x},\frac{dy}{dt}=v_{0y}\\ x=x_0,y=y_0\end{array}}$

El caso más simple es el de una partícula que parte del origen con velocidad v_0x

${\displaystyle t=0\{\begin{array}{l}\frac{dx}{dt}=v_{0x},\frac{dy}{dt}=0\\ x=\mathrm{0,}y=0\end{array}}$

El resultado es

${\displaystyle \{\begin{array}{l}0=C\\ v_{0x}=D\end{array}}$

La posición de la partícula (x, y) en función del tiempo t es

${\displaystyle \zeta =v_{0x}t\exp (-i\Omega t),\{\begin{array}{l}x=v_{0x}t\cos (\Omega t)\\ y=-v_{0x}t\sin (\Omega t)\end{array}}$

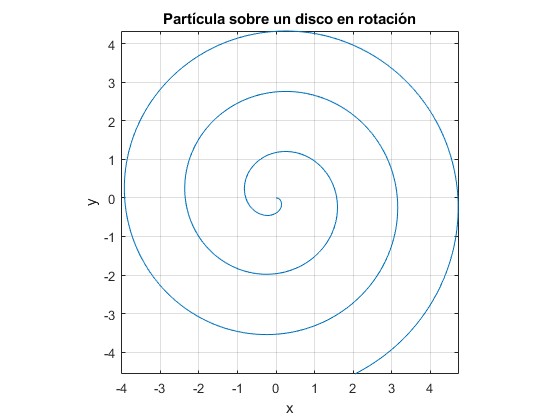
Representamos la trayectoria de la partícula que desliza sin rozamiento sobre disco que gira alrededor de su eje vertical con velocidad angular constante Ω= 1 rad/s. La partícula parte del origen con velocidad v_0x=0.25 m/s

w=1; %velocidad angular de rotación
v0=0.25; %velocidad inicial en X
fplot(@(t) v0*t.*cos(w*t), @(t) -v0*t.*sin(w*t), [0,20])
grid on
axis equal
xlabel('x')
ylabel('y');
title('Partícula sobre un disco en rotación')

Coordenadas polares

Es conveniente expresar las ecuaciones del movimiento en coordenadas polares. La posición, velocidad y aceleración son

${\displaystyle \{\begin{array}{l}\overrightarrow{r}=r\widehat{r}\\ \overrightarrow{v}=\frac{d\overrightarrow{r}}{dt}=\frac{dr}{dt}\widehat{r}+r\frac{d\theta }{dt}\widehat{\theta }\\ \frac{d^2\overrightarrow{r}}{d{t}^2}=\left(\frac{d^{2}r}{d{t}^2}-r{\left(\frac{d\theta }{dt}\right)}^2\right)\widehat{r}+\left(r\frac{d^2\theta }{d{t}^2}+2\frac{dr}{dt}\frac{d\theta }{dt}\right)\widehat{\theta }\end{array}}$

La ecuación del movimiento es

${\displaystyle \{\begin{array}{l}\frac{d^{2}r}{d{t}^2}-r{\left(\frac{d\theta }{dt}\right)}^2={\Omega }^{2}r-\frac{{\mu }_{k}g}{\sqrt{{\left(\frac{dr}{dt}\right)}^2+r^2{\left(\frac{d\theta }{dt}\right)}^2}}\frac{dr}{dt}+2\Omega r\frac{d\theta }{dt}\\ r\frac{d^2\theta }{d{t}^2}+2\frac{dr}{dt}\frac{d\theta }{dt}=-\frac{{\mu }_{k}g}{\sqrt{{\left(\frac{dr}{dt}\right)}^2+r^2{\left(\frac{d\theta }{dt}\right)}^2}}r\frac{d\theta }{dt}-2\Omega \frac{dr}{dt}\end{array}}$

Expresamos la ecuación del movimiento en términos de dos variables adimensionales τ y ξ

${\displaystyle \begin{array}{l}\tau =t\Omega \\ \xi =\frac{r}{R}=\frac{r{\Omega }^2}{{\mu }_{k}g}\\ \{\begin{array}{l}\frac{d^2\xi }{d{\tau }^2}-\xi {\left(\frac{d\theta }{d\tau }\right)}^2=\xi -\frac{1}{\sqrt{{\left(\frac{d\xi }{d\tau }\right)}^2+{\xi }^2{\left(\frac{d\theta }{dt}\right)}^2}}\frac{d\xi }{d\tau }+2\xi \frac{d\theta }{d\tau }\\ \xi \frac{d^2\theta }{d{\tau }^2}+2\frac{d\xi }{d\tau }\frac{d\theta }{d\tau }=-\frac{1}{\sqrt{{\left(\frac{d\xi }{d\tau }\right)}^2+{\xi }^2{\left(\frac{d\theta }{d\tau }\right)}^2}}\xi \frac{d\theta }{d\tau }-2\frac{d\xi }{d\tau }\end{array}\end{array}}$

La circunferencia crítica tiene un radio de ξ=1

Se resuelve el sistema de dos ecuaciones diferenciales por procedimientos numéricos

Examinamos los casos en los que la partícula parte de un punto dentro de la circunferencia crítica ξ<1 con velocidad no nula. A continuación, los casos en los que la partícula parte de puntos situados fuera de la circunferencia de radio unidad

• La partícula parte del origen, ξ=0, θ=0, con velocidad dξ/dτ=2, dθ/dτ=0. Observamos la trayectoria durante un tiempo τ=1

function disco
    ang=(0:360)*pi/180; %disco
    hold on
    fill(cos(ang),sin(ang),'c','FaceAlpha',.3)

    opts=odeset('events',@stop_particula);
    % x(1) es r, x(2) dr/dt, x(3) es th, x(4) dth/dt
    fg=@(t,x)[x(2); x(1)*x(4)^2+x(1)+2*x(1)*x(4)-x(2)/sqrt(x(2)^2+
x(1)^2*x(4)^2); x(4); -2*x(2)*x(4)/x(1)-2*x(2)/x(1)-x(4)/sqrt(x(2)^2+
x(1)^2*x(4)^2)];
    [t,x]=ode45(fg,[0,1],[eps, 2, 0, 0], opts);
    xx=x(:,1).*cos(x(:,3));
    yy=x(:,1).*sin(x(:,3));
    plot(xx,yy)
    plot(xx(1),yy(1),'ro','markersize',3,'markerfacecolor','r')
    plot(xx(end),yy(end),'bo','markersize',3,'markerfacecolor','b')
    hold off
    axis equal
    disp(t(end))
    grid on
    xlabel('x')
    ylabel('y');
    title('Partícula sobre un disco en rotación')

    function [value,isterminal,direction]=stop_particula(~,x)
        v2=10;
        if x(2)^2+x(1)^2*x(4)^2<1e-6 %detiene
            v2=0;
        end
        value=v2;
        isterminal=1;   
        direction=-1; 
    end

end



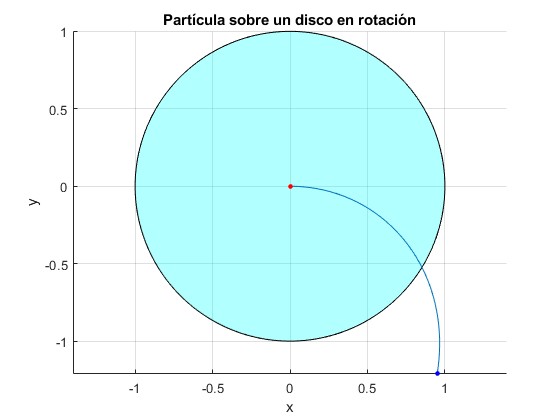
• La partícula parte del origen, ξ=0, θ=0, con velocidad dξ/dτ=1.15, dθ/dτ=0. Observamos la trayectoria hasta que se detiene en el instante τ=2.75



 2.7454

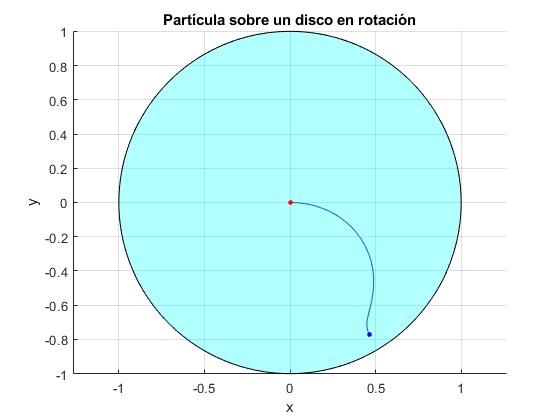
• La partícula parte de la posición, ξ=0.95 (en el interior de la circunferencia, cerca del borde), θ=0, con velocidad dξ/dτ=-1.6, dθ/dτ=-1. Observamos la trayectoria hasta que se detiene en el instante τ=1.86



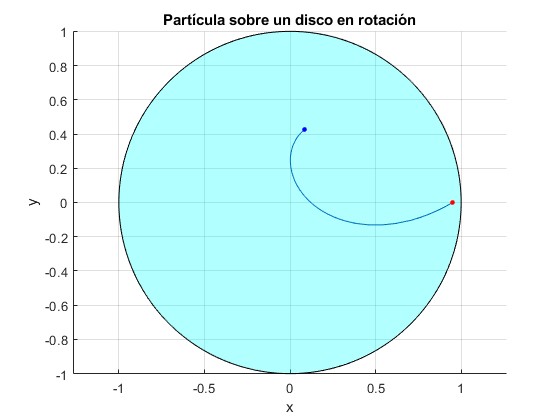
• La partícula parte de la posición, ξ=1.25 (fuera de la circunferencia), θ=0, con velocidad dξ/dτ=-1.5, dθ/dτ=-0.5. Observamos la trayectoria hasta que se detiene dentro de la circunferencia en el instante τ=1.62



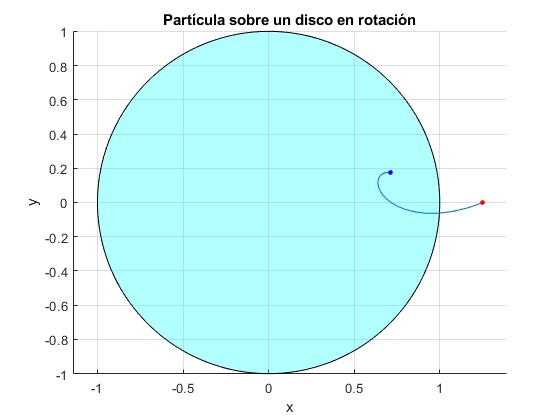
• La partícula parte de la posición, ξ=1.25 (fuera de la circunferencia), θ=0, con velocidad dξ/dτ=-2, dθ/dτ=-1. La partícula sale fuera del disco, observamos la trayectoria durante τ=3



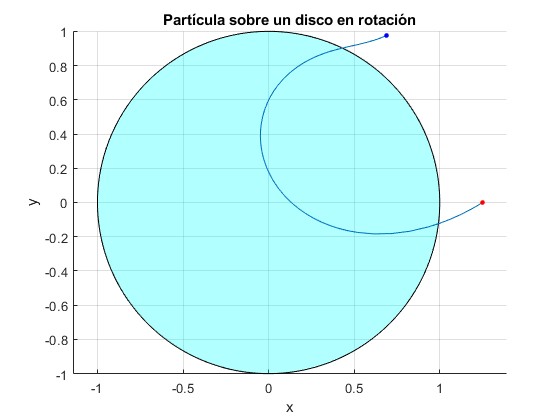
• La partícula parte de la posición, ξ=1.25 (fuera de la circunferencia), θ=0, con velocidad dξ/dτ=-1, dθ/dτ=-0.25. Se acerca a la circunferencia y luego, se aleja deslizando sobre el disco. Observamos la trayectoria durante τ=5

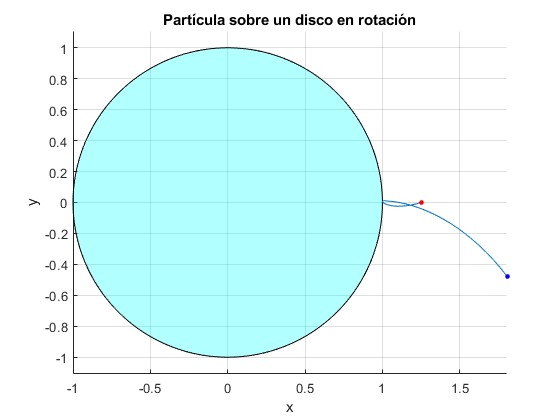
Observamos la trayectoria de la partícula deslizando en un disco de radio muy grande

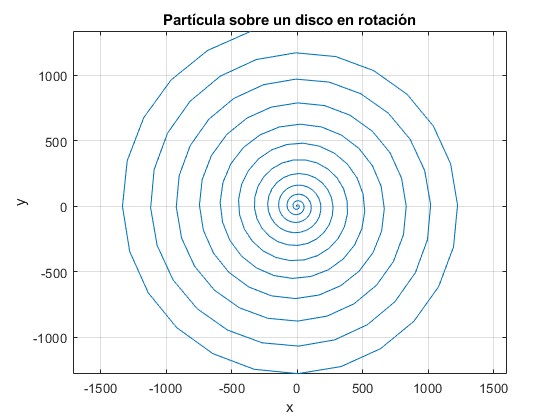
La partícula parte del origen, ξ=0, θ=0, con velocidad dξ/dτ=2, dθ/dτ=0. Observamos su movimiento en espiral durante τ=80

% x(1) es r, x(2) dr/dt, x(3) es th, x(4) dth/dt
fg=@(t,x)[x(2); x(1)*x(4)^2+x(1)+2*x(1)*x(4)-x(2)/sqrt(x(2)^2+x(1)^2*x(4)^2);
 x(4); -2*x(2)*x(4)/x(1)-2*x(2)/x(1)-x(4)/sqrt(x(2)^2+x(1)^2*x(4)^2)];
[~,x]=ode45(fg,linspace(0,80,300),[eps, 2, 0, 0]);
xx=x(:,1).*cos(x(:,3));
yy=x(:,1).*sin(x(:,3));
plot(xx,yy)
axis equal
grid on
xlabel('x')
ylabel('y');
title('Partícula sobre un disco en rotación')

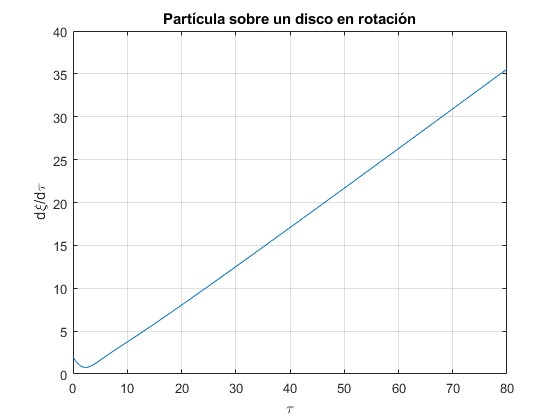
Representamos la velocidad radial dξ/dτ en función del tiempo τ. Después de un cierto tiempo, vemos que esta velocidad se incrementa linealmente con el tiempo. Las condiciones iniciales son ξ=0, θ=0, con velocidad dξ/dτ=2, dθ/dτ=0

 % x(1) es r, x(2) dr/dt, x(3) es th, x(4) dth/dt
fg=@(t,x)[x(2); x(1)*x(4)^2+x(1)+2*x(1)*x(4)-x(2)/sqrt(x(2)^2+x(1)^2*x(4)^2); 
x(4); -2*x(2)*x(4)/x(1)-2*x(2)/x(1)-x(4)/sqrt(x(2)^2+x(1)^2*x(4)^2)];
[t,x]=ode45(fg,linspace(0,80,300),[eps, 2, 0, 0]);
plot(t,x(:,2))
grid on
xlabel('\tau')
ylabel('d\xi/d\tau');
title('Partícula sobre un disco en rotación')

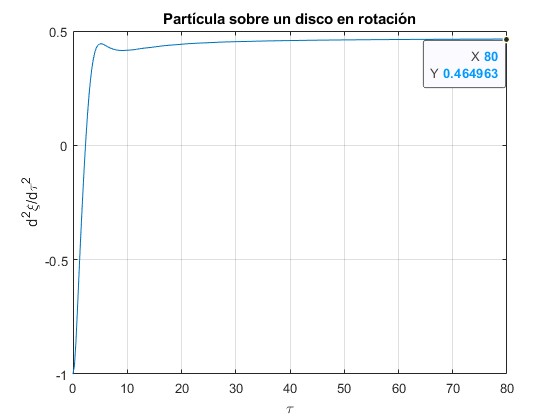
Representamos la aceleración radial d²ξ/dτ² en función del tiempo τ. Después de un cierto tiempo, vemos que tiende al valor constante que es independiente de las condiciones iniciales. Probar tambien con ξ=1, θ=0, con velocidad dξ/dτ=2, dθ/dτ=0

fg=@(t,x)[x(2); x(1)*x(4)^2+x(1)+2*x(1)*x(4)-x(2)/sqrt(x(2)^2+x(1)^2*x(4)^2); 
x(4); -2*x(2)*x(4)/x(1)-2*x(2)/x(1)-x(4)/sqrt(x(2)^2+x(1)^2*x(4)^2)];
[t,x]=ode45(fg,linspace(0,80,300),[eps, 2, 0, 0]);
acel=x(:,1).*x(:,4).^2+x(:,1)+2*x(:,1).*x(:,4)-x(:,2)./sqrt(x(:,2).^2+
x(:,1).^2.*x(:,4).^2);
plot(t,acel)
grid on
xlabel('\tau')
ylabel('d^2\xi/d\tau^2');
title('Partícula sobre un disco en rotación')

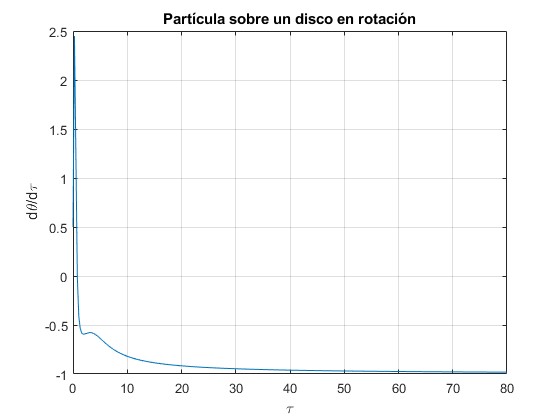
Representamos la velocidad angular dθ/dτ en función del tiempo τ. Después de un cierto tiempo, vemos que esta velocidad se mantiene constante e igual a -1. Las condiciones iniciales son ξ=1, θ=0, con velocidad dξ/dτ=-2, dθ/dτ=0.5

 % x(1) es r, x(2) dr/dt, x(3) es th, x(4) dth/dt
fg=@(t,x)[x(2); x(1)*x(4)^2+x(1)+2*x(1)*x(4)-x(2)/sqrt(x(2)^2+x(1)^2*x(4)^2);
 x(4); -2*x(2)*x(4)/x(1)-2*x(2)/x(1)-x(4)/sqrt(x(2)^2+x(1)^2*x(4)^2)];
[t,x]=ode45(fg,linspace(0,80,300),[1, -2, 0, 0.5]);
plot(t,x(:,4))
grid on
xlabel('\tau')
ylabel('d\theta/d\tau');
title('Partícula sobre un disco en rotación')

Sistema de Referencia inercial

Como hemos apreciado, una partícula en reposo sobre la plataforma en rotación describe una trayectoria circular de radio r respecto al Sistema de Referencia Inercial o Sistema de Laboratorio. En este apartado, vamos a describir el movimiento de la partícula en este Sistema de Referencia

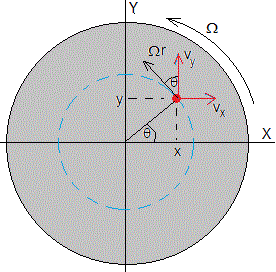
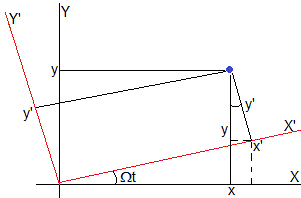
Sea una partícula de masa m que está situada sobre una plataforma en rotación con velocidad angular constante Ω. En un instante dado t, la posición de la partícula es (x, y) y su velocidad (v_x, v_y) referidas a Sistema de Referencia Inercial OXY. El vector velocidad relativa de la partícula respecto a la plataforma es

${\displaystyle \begin{array}{l}\overrightarrow{v_r}=\left(v_x+\Omega r\sin \theta \right)\widehat{i}+\left(v_y-\Omega r\cos \theta \right)\widehat{j}=\\ \left(v_x+\Omega y\right)\widehat{i}+\left(v_y-\Omega x\right)\widehat{j}\end{array}}$

La fuerza de rozamiento que ejerce la plataforma sobre la partícula cuando desliza, es constante en módulo, μ_k·N=μ_k·mg y de sentido contrario a la dirección de la velocidad relativa. μ_k es el coeficiente cinético

${\displaystyle \overrightarrow{F_r}=-{\mu }_{k}mg\frac{\left(v_x+\Omega y\right)\widehat{i}+\left(v_y-\Omega x\right)\widehat{j}}{\sqrt{{\left(v_x+\Omega y\right)}^2+{\left(v_y-\Omega x\right)}^2}}}$

Las ecuaciones del movimiento cuando el cuerpo desliza son:

${\displaystyle \begin{array}{l}\frac{d^{2}x}{d{t}^2}=-{\mu }_{k}g\frac{v_x+\Omega y}{\sqrt{{\left(v_x+\Omega y\right)}^2+{\left(v_y-\Omega x\right)}^2}}\\ \frac{d^{2}y}{d{t}^2}=-{\mu }_{k}g\frac{v_y-\Omega x}{\sqrt{{\left(v_x+\Omega y\right)}^2+{\left(v_y-\Omega x\right)}^2}}\end{array}}$

Ecuaciones del movimiento

Las ecuaciones del movimiento en coordendas polares son

${\displaystyle m\overrightarrow{a}=\overrightarrow{F_r}\{\begin{array}{l}\frac{d^{2}r}{d{t}^2}-r{\left(\frac{d\theta }{dt}\right)}^2=-{\mu }_{k}g\frac{\frac{dr}{dt}}{\sqrt{{\left(\frac{dr}{dt}\right)}^2+r^2{\left(\frac{d\theta }{dt}-\Omega \right)}^2}}\\ r\frac{d^2\theta }{d{t}^2}+2\frac{dr}{dt}\frac{d\theta }{dt}=-{\mu }_{k}gr\frac{\frac{d\theta }{dt}-\Omega }{\sqrt{{\left(\frac{dr}{dt}\right)}^2+r^2{\left(\frac{d\theta }{dt}-\Omega \right)}^2}}\end{array}}$

Simplificamos las ecuaciones definiendo las variables adimensiones τ=t·Ω y ξ=r/R=rΩ²/(μ_k·mg).

${\displaystyle \{\begin{array}{l}\frac{d^2\xi }{d{\tau }^2}-\xi {\left(\frac{d\theta }{d\tau }\right)}^2=-\frac{\frac{d\xi }{d\tau }}{\sqrt{{\left(\frac{d\xi }{d\tau }\right)}^2+{\xi }^2{\left(1-\frac{d\theta }{d\tau }\right)}^2}}\\ \xi \frac{d^2\theta }{d{\tau }^2}+2\frac{d\xi }{d\tau }\frac{d\theta }{d\tau }=\xi \frac{1-\frac{d\theta }{d\tau }}{\sqrt{{\left(\frac{d\xi }{d\tau }\right)}^2+{\xi }^2{\left(1-\frac{d\theta }{d\tau }\right)}^2}}\end{array}}$

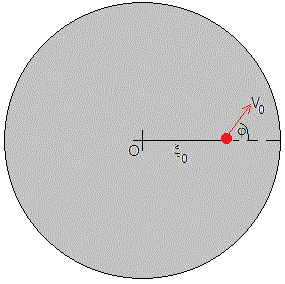
Las condiciones iniciales son las siguientes:

Se lanza la partícula en el instante τ=0, desde la posición ξ₀, con velocidad V₀ haciendo un ángulo φ en el sistema de referencia de la plataforma

Las componentes de la velocidad inicial de la partícula medida en el Sistema de Referencia Inercial respecto del cual la plataforma gira con velocidad angular de una unidad (en el sistema de unidades establecido) es

${\displaystyle \begin{array}{l}{\left(\frac{d\xi }{d\tau }\right)}_0=V_0\cos \phi \\ {\xi }_{{}_0}{\left(\frac{d\theta }{d\tau }\right)}_0=V_0\sin \phi +{\xi }_0·1=V_0\sin \phi +{\xi }_0\\ {\left(\frac{d\theta }{d\tau }\right)}_0=\frac{V_0\sin \phi }{{\xi }_0}+1\end{array}}$

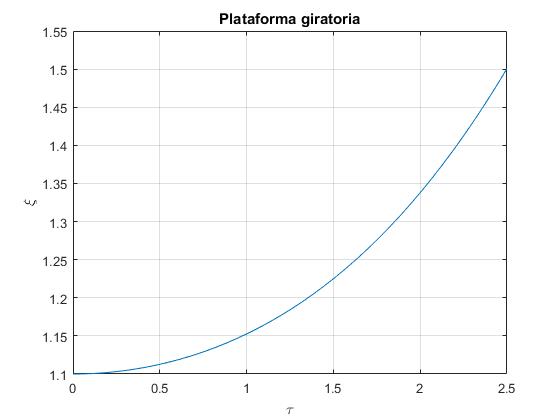
Partícula en reposo

Si la partícula parte del reposo, V₀=0, con respecto a la plataforma desde una posición ξ₀<1 (r<R) la partícula continuará en reposo sobre la plataforma en dicha posición. Consideremos que la posición inicial de la partícula en reposo sobre la plataforma es ξ₀>1

x0=[1.1,eps,0,1]; %eps evita la división 0/0
%x(1) x, x(2) dx/dt, x(3) dth
fg=@(t,x)[x(2); x(4)^2*x(1)-x(2)/sqrt(x(1)^2*(1-x(4))^2+x(2)^2); x(4); 
-2*x(2)*x(4)/x(1)+(1-x(4))/sqrt(x(1)^2*(1-x(4))^2+x(2)^2)];
[t,x]=ode45(fg,[0,2.5],x0);
plot(t,x(:,1))
grid on
xlabel('\tau')
ylabel('\xi');
title('Plataforma giratoria')

Partícula en movimiento relativo

Dibujamos las trayectorias de partículas vistas por el observador inercial para tres condiciones iniciales diferentes:

• La trayectoria '1' corresponde a las condiciones iniciales: ξ₀=0.5, V₀=1 y φ=π.
• La trayectoria '2' corresponde a las condiciones iniciales: ξ₀=0.5, V₀=0.6 y φ=0.
• La trayectoria '3' corresponde a las condiciones iniciales: ξ₀=1.1, V₀=1.3 y φ=1.2π.

%x(1) x, x(2) dx/dt, x(3) dth
fg=@(t,x)[x(2); x(4)^2*x(1)-x(2)/sqrt(x(1)^2*(1-x(4))^2+x(2)^2); x(4); 
-2*x(2)*x(4)/x(1)+(1-x(4))/sqrt(x(1)^2*(1-x(4))^2+x(2)^2)];

hold on
x0=[0.5,-1,0,1];
[t,x]=ode45(fg,[0,10],x0);
plot(x(:,1).*cos(x(:,3)), x(:,1).*sin(x(:,3))) 
x0=[0.5,0.6,0,1];
[t,x]=ode45(fg,[0,10],x0);
plot(x(:,1).*cos(x(:,3)), x(:,1).*sin(x(:,3))) 
x0=[1.1,1.3*cos(1.2*pi),0,1+1.3*sin(1.2*pi)/1.1];
[t,x]=ode45(fg,[0,10],x0);
plot(x(:,1).*cos(x(:,3)), x(:,1).*sin(x(:,3))) 
hold off
grid on
legend('1','2','3')
axis equal
xlabel('\xi·cos\theta')
ylabel('\xi·sin\theta');
title('Plataforma giratoria')

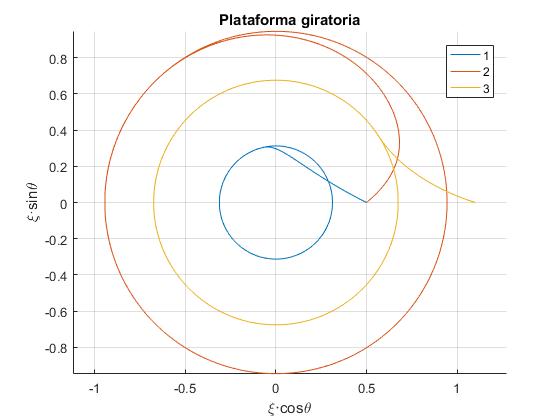
Lo curioso de la última trayectoria, es que una partícula con ξ₀>1, acaba en reposo sobre la plataforma en la región ξ<1

Dibujamos las trayectorias de partículas vistas por el observador inercial para dos condiciones iniciales diferentes muy próximas:

• La trayectoria azul corresponde a las condiciones iniciales: ξ₀=0.2, V₀=0.97 y φ=0.
• La trayectoria rosa corresponde a las condiciones iniciales: ξ₀=0.2, V₀=0.971 y φ=0.

d=0.2; %distancia al origen
fg=@(t,x)[x(2); x(4)^2*x(1)-x(2)/sqrt(x(1)^2*(1-x(4))^2+x(2)^2); x(4);
 -2*x(2)*x(4)/x(1)+(1-x(4))/sqrt(x(1)^2*(1-x(4))^2+x(2)^2)];

hold on
V0=0.97; %velocidad inicial (referido a la plataforma)
angulo=0; %ángulo (grados)
x0=[d,V0*cos(angulo*pi/180),0,1+V0*sin(angulo*pi/180)/d];
[t,x]=ode45(fg,[0,10],x0);
plot(x(:,1).*cos(x(:,3)), x(:,1).*sin(x(:,3))) 

V0=0.971;
angulo=0;
x0=[d,V0*cos(angulo*pi/180),0,1+V0*sin(angulo*pi/180)/d];
[t,x]=ode45(fg,[0,10],x0);
plot(x(:,1).*cos(x(:,3)), x(:,1).*sin(x(:,3))) 
hold off
grid on
axis equal
xlabel('\xi·cos\theta')
ylabel('\xi·sin\theta');
title('Plataforma giratoria')

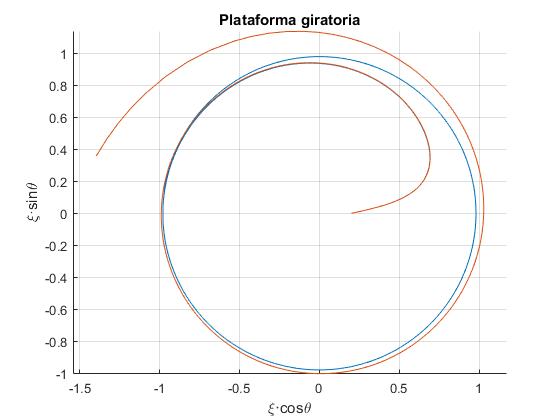
La primera partícula acaba en reposo sobre la plataforma a una distancia ξ<1 del origen. Mientras que la otra se va al infinito ξ→∞

Fijada una distancia ξ₀<1, podríamos investigar, para qué velocidades V₀ y ángulos φ la partícula escapa al infinito

Comprobación

• Hemos descrito el movimiento de la partícula en el Sistema de Referencia inercial

${\displaystyle \{\begin{array}{l}\frac{d^2\xi }{d{\tau }^2}-\xi {\left(\frac{d\theta }{d\tau }\right)}^2=-\frac{\frac{d\xi }{d\tau }}{\sqrt{{\left(\frac{d\xi }{d\tau }\right)}^2+{\xi }^2{\left(1-\frac{d\theta }{d\tau }\right)}^2}}\\ \xi \frac{d^2\theta }{d{\tau }^2}+2\frac{d\xi }{d\tau }\frac{d\theta }{d\tau }=\xi \frac{1-\frac{d\theta }{d\tau }}{\sqrt{{\left(\frac{d\xi }{d\tau }\right)}^2+{\xi }^2{\left(1-\frac{d\theta }{d\tau }\right)}^2}}\end{array}}$

Resolvemos el sistema de ecuaciones diferenciales para las condiciones iniciales: la partícula parte del origen (ξ=0, θ=0) con velocidad dξ/dτ=2, dθ/dτ=0

• Hemos descrito el movimiento de la partícula en el Sistema de Referencia no inercial

${\displaystyle \{\begin{array}{l}\frac{d^2\xi }{d{\tau }^2}-\xi {\left(\frac{d\theta }{d\tau }\right)}^2=\xi -\frac{1}{\sqrt{{\left(\frac{d\xi }{d\tau }\right)}^2+{\xi }^2{\left(\frac{d\theta }{dt}\right)}^2}}\frac{d\xi }{d\tau }+2\xi \frac{d\theta }{d\tau }\\ \xi \frac{d^2\theta }{d{\tau }^2}+2\frac{d\xi }{d\tau }\frac{d\theta }{d\tau }=-\frac{1}{\sqrt{{\left(\frac{d\xi }{d\tau }\right)}^2+{\xi }^2{\left(\frac{d\theta }{d\tau }\right)}^2}}\xi \frac{d\theta }{d\tau }-2\frac{d\xi }{d\xi }\end{array}}$

Resolvemos el sistema de ecuaciones diferenciales con las mismas condiciones iniciales: la partícula parte del origen (ξ=0, θ=0) con velocidad dξ/dτ=2, dθ/dτ=0

Relacionamos los dos sistemas mediante una simple transformación

${\displaystyle \{\begin{array}{l}x=x\text{'}\cos \left(\Omega t\right)-y\text{'}\sin \left(\Omega t\right)\\ y=x\text{'}\sin \left(\Omega t\right)+y\text{'}\cos \left(\Omega t\right)\end{array}}$

hold on
%Sistema de Referencia inercial
f=@(t,x)[x(2); x(4)^2*x(1)-x(2)/sqrt(x(1)^2*(1-x(4))^2+x(2)^2); x(4);
 -2*x(2)*x(4)/x(1)+(1-x(4))/sqrt(x(1)^2*(1-x(4))^2+x(2)^2)];
[~,x]=ode45(f,[0,10],[eps, 2, 0, 0]);
plot(x(:,1).*cos(x(:,3)),x(:,1).*sin(x(:,3)),'b') 
%Sistema de Referencia no inercial
g=@(t,x)[x(2); x(1)*x(4)^2+x(1)+2*x(1)*x(4)-x(2)/sqrt(x(2)^2+x(1)^2*x(4)^2);
 x(4); -2*x(2)*x(4)/x(1)-2*x(2)/x(1)-x(4)/sqrt(x(2)^2+x(1)^2*x(4)^2)];
[t,x]=ode45(g,[0,10],[eps, 2, 0, 0]);
x1=x(:,1).*cos(x(:,3));
y1=x(:,1).*sin(x(:,3));
plot(x1,y1,'r')
%relación
xx=x1.*cos(t)-y1.*sin(t);
yy=x1.*sin(t)+y1.*cos(t);
plot(xx,yy,'k')

hold off
axis equal
grid on
xlabel('x')
ylabel('y');
title('Partícula sobre un disco en rotación')

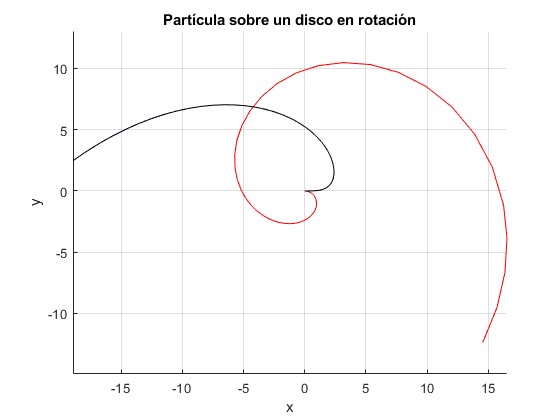
• En color rojo, la trayectoria en el Sistema de Referencia no inercial, que se obtiene resolviendo el segundo sistema de dos ecuaciones diferenciales
• En color azul, la trayectoria en el Sistema de Referencia inercial, que se obtiene resolviendo el primer sistema de dos ecuaciones diferenciales
• En color negro, la trayectoria en el Sistema de Referencia inercial obtenida a partir de la trayectoria en el Sistema de Referencia no inercial mediante la transformación

Referencias

YU Feng-jun. The motion of a particle on a non - smooth rotating disk. Volume 37, n° 2, 2018

Akshat Agha, Sahil Gupta, Toby Joseph. Particle sliding on a turntable in the presence of friction. Am. J. Phys. 83 (2) February 2015 pp 126-132