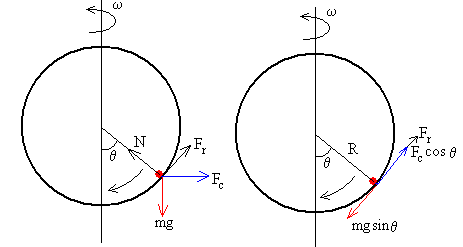
Consideremos un aro de radio R que puede girar alrededor de su diámetro vertical con velocidad angular ω. Un punto material de masa m se mueve a lo largo de la circunferencia sin rozamiento. Su posición está dada por el ángulo θ tal como se señala en la figura.

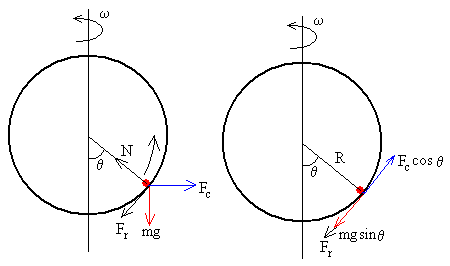
Las fuerzas que actúan sobre la partícula, cuando estamos situados en el Sistema de Referencia en rotación son:

• El peso, mg
• La fuerza centrífuga, F_c=mω²Rsinθ
• La reacción N de la superficie circular.

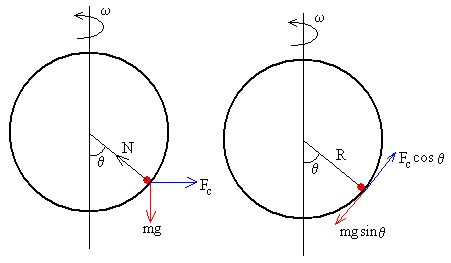
Descomponemos las fuerzas en la dirección vertical y horizontal. En la situación de equilibrio, se cumplirá que

N·cosθ =mg
N·sinθ =F_c

N=mgcosθ+F_csinθ=mgcosθ+mω²Rsin²θ

Energía potencial. Posiciones de equilibrio

Si descomponemos las fuerzas en la dirección tangencial y normal a la circunferencia, tendremos que en la situación de equilibrio

mg·sinθ =F_c·cosθ  

La partícula está en equilibrio en la dirección normal. Si no está en equilibrio en la dirección tangencial, la fuerza neta en esta dirección es

F= -mg·sinθ +F_c·cosθ= -mg·sinθ +mω²·R·sinθ ·cosθ

Esta fuerza depende solamente de la posición θ  y es conservativa. La energía potencial correspondiente a la fuerza F(θ) es

${\displaystyle {\displaystyle \underset{0}{\overset{\theta }{\int }}F(\theta )R·d\theta }=E_p(0)-E_P(\theta )}$

Tomando como nivel cero de energía potencial E_p(0)=0 para θ=0, integramos y haciendo algunas operaciones, se obtiene

${\displaystyle E_p(\theta )=mgR(1-\cos \theta )-\frac{1}{2}m{\omega }^2{R}^2{\sin }^2\theta }$

• Para ω²<g/R, la curva de la energía potencial E_p(θ) presenta un mínimo en θ_e=0 o posición de equilibrio estable.

Supongamos que la partícula de masa m parte de la posición θ₀ en reposo. Su energía es E=E_p(θ₀). Como la energía potencial es una función simétrica, la partícula se mueve entre las posiciones angulares (-θ₀, θ₀)



• Para ω²>g/R, la curva de la energía potencial E_p(θ) presenta un mínimo para

${\displaystyle \frac{d{E}_p(\theta )}{d\theta }=\left(mgR-m{\omega }^2{R}^2\cos \theta \right)\sin \theta =\mathrm{0,}\{\begin{array}{l}\sin {\theta }_m=\mathrm{0,}{\theta }_m=0\\ \cos {\theta }_e=\frac{g}{{\omega }^{2}R}\end{array}}$

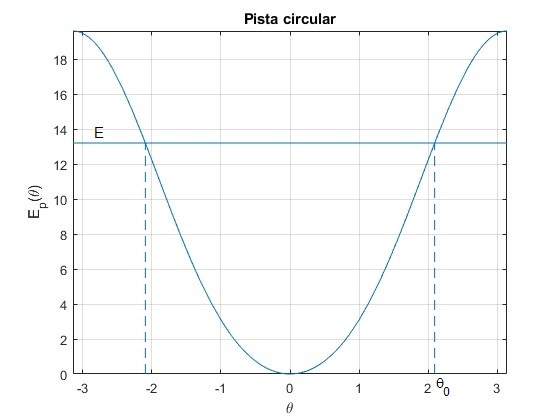
posición de equilibrio estable θ_e y un máximo local para θ_m=0, posición de equilibrio inestable. La energía potencial mínima para θ_e vale

${\displaystyle E_m=mgR-\frac{1}{2}m\frac{g^2}{{\omega }^2}-\frac{1}{2}m{\omega }^2{R}^2}$

Hay dos posibles casos

• Cuando la la energía de la partícula E>0

Supongamos que la partícula de masa m parte de la posición θ₀ en reposo. Su energía es E=E_p(θ₀). Como la energía potencial es una función simétrica, la partícula se mueve entre las posiciones angulares (-θ₀, θ₀)



• Cuando la la energía de la partícula E_m<E<0

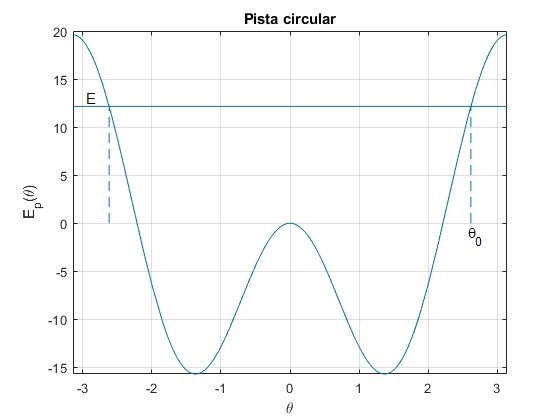
Si la energía de la partícula es negativa E<0, y mayor que la mínima E_m, la partícula se moverá entre θ₀ y θ₁ (figura más abajo)

${\displaystyle \begin{array}{l}E=mgR\left(1-\cos \theta \right)-\frac{1}{2}m{\omega }^2{R}^2{\sin }^2\theta \\ \frac{2\left(E-mgR\right)}{m{R}^2}+{\omega }^2{\sin }^2\theta +2\frac{g}{R}\cos \theta =0\\ {\cos }^2\theta -2\frac{g/R}{{\omega }^2}\cos \theta -\frac{2\left(E-mgR\right)}{m{R}^2{\omega }^2}-1=0\\ \cos {\theta }_{\mathrm{0,1}}=\lambda \pm \sqrt{{\lambda }^2+C},\{\begin{array}{l}C=\frac{2\left(E-mgR\right)}{m{R}^2{\omega }^2}+1\\ \lambda =\frac{g}{R{\omega }^2}\end{array}\end{array}}$

Una de las raíces de la ecuación de segundo grado es cosθ₀ y la otra cosθ₁

w=7; %velocidad angular de rotación
R=1; %radio de la pista circular
Ep=@(x) 9.8*R*(1-cos(x))-w^2*R^2*sin(x).^2/2;
fplot(Ep,[-pi,pi])
th_0=2*pi/3; %ángulo inicial, 120º, parte del reposo
E=Ep(th_0); %energía constante
line([-pi,pi],[E,E])
C=2*(E-9.8*R)/(R*w)^2+1; %constantes
lambda=9.8/(R*w^2); 
if (lambda<1 && E<0)
    th_1=acos(lambda+sqrt(lambda^2+C));
    th_2=acos(lambda-sqrt(lambda^2+C));
else
    th_1=th_0;
    th_2=-th_0;
end
line([th_1,th_1],[0, E], 'lineStyle', '--')
line([th_2,th_2],[0, E], 'lineStyle', '--')
Emin=9.8*R-9.8^2/(2*w^2)-w^2*R^2/2;
grid on
xlabel('\theta')
ylabel('E_p(\theta)')
title('Pista circular')



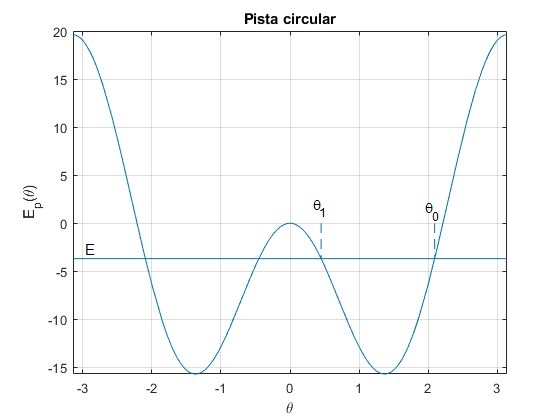
La partícula se puede mover en el intervalo angular (θ₁, θ₀) o bien, en el intervalo simétrico (-θ₁, -θ₀)

Ejemplo.

• Velocidad angular de rotación, ω=7.0 rad/s
• Radio de la pista circular, R=1.0 m
• Posición angular inicial, θ₀=120º

Calculamos la energía total E de la partícula y los ángulos θ₁=25.8° y θ₀=120° (posición de partida)

>> E
E =   -3.6750
>> [th_1,th_2]*180/p
ans =   25.8419  120.0000

Descripción cualitativa del movimiento de la partícula

La partícula parte del reposo en la posición θ₀. Su energía total E es

${\displaystyle E=E_p({\theta }_0)=mgR(1-\cos {\theta }_0)-\frac{1}{2}m{\omega }^2{R}^2{\sin }^2{\theta }_0}$

• Cuando ω²<g/R

La curva de energía potencial E_p(θ) se muestra en la figura en color azul.



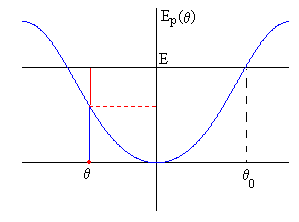
La partícula se desplaza desde la posición inicial θ₀ hacia la posición de equilibrio θ=0. En dicha posición, la energía potencial es mínima E_p(0)=0 y la energía cinética de la partícula es máxima, a continuación, se desplaza hasta la posición simétrica θ=-θ₀ donde su velocidad vuelve a ser cero, retornando posteriormente a la posición de equilibrio.

En la posición θ de la figura, el segmento de color azul mide la energía potencial y el segmento de color rojo, la energía cinética.

La partícula oscila alrededor de la posición de equilibrio estable θ=0 con un determinado periodo.

• Cuando ω²>g/R, hay dos posiblidades

La curva de energía potencial E_p(θ) se muestra en las figuras en color azul.

• cuando la energía E<0, a la izquierda en la figura
• cuando E>0, a la derecha



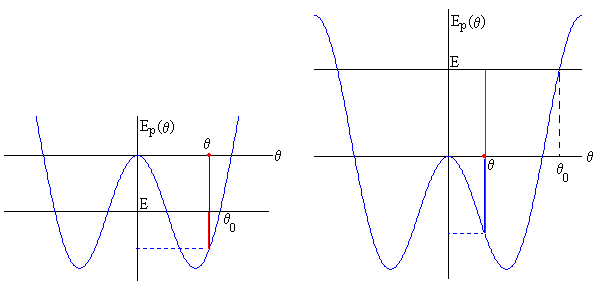
La partícula se desplaza desde la posición inicial θ₀ hacia la posición de equilibrio

${\displaystyle {\theta }_e=\arccos \left(\frac{g}{{\omega }^{2}R}\right)}$

En la figura de la izquierda, la energía total E<0 y la partícula oscila alrededor de la posición de equilibrio estable θ_e.

En la posición θ de la figura, el segmento de color azul mide la energía potencial y el segmento de color rojo, la energía cinética. La energía potencial es mínima en la posición de equilibrio y la energía cinética es máxima.

Los puntos de retorno, aquellos en los que la velocidad es nula y por tanto, la partícula inicia el movimiento en sentido contrario,.

Sin rozamiento

La ecuación del movimiento es, fuerza neta F igual a la masa por aceleración tangencial

${\displaystyle \begin{array}{l}mR\frac{d^2\theta }{d{t}^2}=F_c\cos \theta -mg\sin \theta \\ mR\frac{d^2\theta }{d{t}^2}=m{\omega }^{2}R\sin \theta \cos \theta -mg\sin \theta \\ \frac{d^2\theta }{d{t}^2}=\left({\omega }^2\cos \theta -\frac{g}{R}\right)\sin \theta \end{array}}$

Se resuelve esta ecuación diferencial por procedimientos numéricos, con las siguientes condiciones iniciales, en el instante t=0, θ=θ₀, dθ/dt=0.

Solución analítica

La energía de la partícula es la suma de la energía cinética y potencial. La partícula se mueve con velocidad R·dθ/dt a lo largo de la pista circular

${\displaystyle E=\frac{1}{2}m{R}^2{\left(\frac{d\theta }{dt}\right)}^2-\frac{1}{2}m{\omega }^2{R}^2{\sin }^2\theta +mgR\left(1-\cos \theta \right)}$

Despejamos la velocidad angular dθ/dt e integramos para obtener la posición angular θ en función del tiempo t

${\displaystyle \begin{array}{l}{\left(\frac{d\theta }{dt}\right)}^2={\omega }^2\left\{\frac{2\left(E-mgR\right)}{m{R}^2{\omega }^2}+1-{\cos }^2\theta +2\frac{g/R}{{\omega }^2}\cos \theta \right\}\\ \omega t={\displaystyle \underset{{\theta }_0}{\overset{\theta }{\int }}\frac{d\theta }{\sqrt{C-{\cos }^2\theta +2\lambda \cos \theta }},\{\begin{array}{l}C=\frac{2\left(E-mgR\right)}{m{R}^2{\omega }^2}+1\\ \lambda =\frac{g}{R{\omega }^2}\end{array}}\end{array}}$

Teniendo en cuenta las relaciones trigonométricas

${\displaystyle \{\begin{array}{l}1+\cos \theta =2{\cos }^2\frac{\theta }{2}\\ 1-\cos \theta =2{\sin }^2\frac{\theta }{2}\end{array}}$

Hacemos el cambio de variable

${\displaystyle \begin{array}{l}x=\tan \frac{\theta }{2}=\sqrt{\frac{1-\cos \theta }{1+\cos \theta }}\\ \cos \theta =\frac{1-x^2}{1+x^2}\\ -\sin \theta ·d\theta =-\frac{4x}{{\left(1+x^2\right)}^2}dx\\ d\theta =\frac{2}{1+x^2}dx\end{array}}$

La integral se expresa en términos de la variable x

${\displaystyle \begin{array}{l}{\displaystyle \int \frac{d\theta }{\sqrt{C-{\cos }^2\theta +2\lambda \cos \theta }}={\displaystyle \int \frac{2dx}{\sqrt{C{\left(1+x^2\right)}^2-{\left(1-x^2\right)}^2+2\lambda \left(1-x^2\right)\left(1+x^2\right)}}}}\\ ={\displaystyle \int \frac{2dx}{\sqrt{a{x}^4+b{x}^2+c}},}\{\begin{array}{l}a=C-1-2\lambda \\ b=2C+2\\ c=C-1+2\lambda \end{array}\end{array}}$

Buscamos en una tabla de integrales (véase la referencias) la solución para cada uno de los dos posibles casos:

1. Cuando la energía total es negativa, E_m<E<0 y mayor que la mínima, para ω²>g/R (λ<1). La partícula se mueve en el intervalo (θ₁, θ₀)

Comprobamos que el coeficiente a es negativo. Expresamos el polinomio como producto de factores

${\displaystyle \begin{array}{l}a{x}^4+b{x}^2+c=(-a)\left(x_0^2-x^2\right)\left(x^2-x_1^2\right)\\ x_{\mathrm{0,1}}^2=\frac{-1-C\pm 2\sqrt{{\lambda }^2+C}}{C-1-2\lambda }=\frac{1+C\pm 2\sqrt{{\lambda }^2+C}}{1+2\lambda -C}\end{array}}$

Comprobamos que x_0,1 se corresponden con las posiciones de retorno θ_0,1

${\displaystyle \begin{array}{l}\cos {\theta }_1=\lambda +\sqrt{{\lambda }^2+C}\\ x_1^2=\frac{1-\cos {\theta }_1}{1+\cos {\theta }_1}\\ x_1^2=\frac{1-\lambda -\sqrt{{\lambda }^2+C}}{1+\lambda +\sqrt{{\lambda }^2+C}}=\frac{\left(1-\lambda -\sqrt{{\lambda }^2+C}\right)\left(1+\lambda -\sqrt{{\lambda }^2+C}\right)}{\left(1+\lambda +\sqrt{{\lambda }^2+C}\right)\left(1+\lambda -\sqrt{{\lambda }^2+C}\right)}=\frac{1+C-2\sqrt{{\lambda }^2+C}}{1+2\lambda -C}\\ \cos {\theta }_0=\lambda -\sqrt{{\lambda }^2+C}\\ x_0^2=\frac{1-\lambda +\sqrt{{\lambda }^2+C}}{1+\lambda -\sqrt{{\lambda }^2-C}}=\frac{\left(1-\lambda +\sqrt{{\lambda }^2+C}\right)\left(1+\lambda +\sqrt{{\lambda }^2+C}\right)}{\left(1+\lambda -\sqrt{{\lambda }^2+C}\right)\left(1+\lambda +\sqrt{{\lambda }^2+C}\right)}=\frac{1+C+2\sqrt{{\lambda }^2+C}}{1+2\lambda -C}\end{array}}$

Buscamos la integral en la Tabla, página 282, 3.152, n° 9

${\displaystyle \begin{array}{l}{\displaystyle \underset{a}{\overset{u}{\int }}\frac{dx}{\sqrt{\left(a^2-x^2\right)\left(x^2-b^2\right)}}}=\frac{1}{a}F\left(\kappa ,q\right),\{\begin{array}{l}\kappa =\arcsin \frac{a}{u}\sqrt{\frac{u^2-b^2}{a^2-b^2}}\\ t=\frac{\sqrt{a^2-b^2}}{a}\end{array},\\ a\ge u>b>0\end{array}}$

El resultado de la integral es

${\displaystyle \begin{array}{l}\omega t=\frac{2}{\sqrt{-a}}{\displaystyle \underset{x_0}{\overset{x}{\int }}\frac{dx}{\sqrt{\left(x_0^2-x^2\right)\left(x^2-x_1^2\right)}}}\\ \omega t=\frac{2}{x_0\sqrt{-a}}F\left(\arcsin \left(\frac{x_0}{x}\sqrt{\frac{x^2-x_1^2}{x_0^2-x_1^2}}\right),\frac{\sqrt{x_0^2-x_1^2}}{x_0}\right)\end{array}}$

Despejamos la variable x, véase la página Integrales elípticas

${\displaystyle \begin{array}{l}\text{sn}\left(\frac{x_0\sqrt{-a}}{2}\omega t,\frac{\sqrt{x_0^2-x_1^2}}{x_0}\right)=\sin \left(\arcsin \left(\frac{x_0}{x}\sqrt{\frac{x^2-x_1^2}{x_0^2-x_1^2}}\right)\right)\\ x=\frac{x_2}{\sqrt{1-\left(1-\frac{x_1^2}{x_0^2}\right){\text{sn}}^2\left(\frac{x_0\sqrt{-a}}{2}\omega t,\frac{\sqrt{x_0^2-x_1^2}}{x_0}\right)}}\end{array}}$

Dehacemos el cambio de variable x=tan(θ/2)

${\displaystyle \theta (t)=2\arctan \frac{x_1}{\sqrt{1-\left(1-\frac{x_1^2}{x_0^2}\right){\text{sn}}^2\left(\frac{x_0\sqrt{-a}}{2}\omega t,\frac{\sqrt{x_0^2-x_1^2}}{x_0}\right)}}}$

Ejemplo.

• Velocidad angular de rotación, ω=7.0 rad/s
• Radio de la pista circular, R=1.0 m
• Posición angular inicial, θ₀=120º

La partícula se mueve entre las posciones angulares θ₀=120° (de partida) y θ₁=25.84°

w=7; %velocidad angular de rotación
R=1; %radio de la pista circular
th_0=2*pi/3; %ángulo inicial, 120º, parte del reposo
E=9.8*R*(1-cos(th_0))-w^2*R^2*sin(th_0).^2/2; %energía constante
C=2*(E-9.8*R)/(R*w)^2+1; %constantes
lambda=9.8/(R*w^2); 
th_1=acos(lambda+sqrt(lambda^2+C)); %posiciones extremas
th_0=acos(lambda-sqrt(lambda^2+C)); 
x0=(1+C+2*sqrt(lambda^2+C))/(1+2*lambda-C); %cuadrado de x_0
x1=(1+C-2*sqrt(lambda^2+C))/(1+2*lambda-C); %cuadrado de x_1
a=C-1-2*lambda; %coeficiente
th=@(t) 2*atan(sqrt(x1)./sqrt(1-(1-x1/x0)*ellipj(sqrt(x0)
*sqrt(-a)*w*t/2,1-x1/x0).^2));
hold on
fplot(th,[0,5])

%solución numérica
f=@(t,x) [x(2); (w^2*cos(x(1))-9.8/R)*sin(x(1))]; 
[t,x]=ode45(f,[0,5],[th_1,0]);
plot(t,x(:,1))
hold off
grid on
xlabel('t')
ylabel('\theta')
set(gca,'YTick',0:pi/6:pi)
set(gca,'YTickLabel',{'0','\pi/6','\pi/3','\pi/2','2\pi/3', '5\pi/6', '\pi'})
legend('analítica','numérica','Location', 'best')
title('Pista circular que gira')



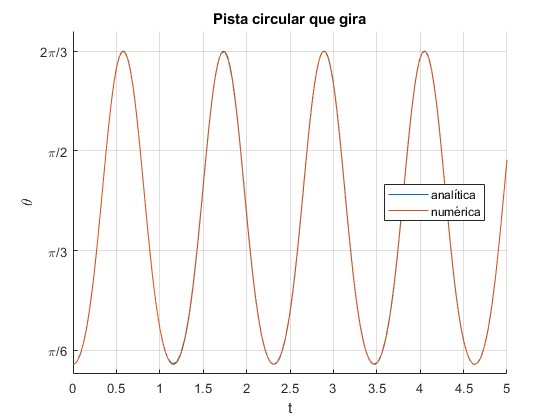
Vemos que la soluciones analítica y numérica, utilizando el procedimiento ode45 de MATLAB, prácticamente coinciden

Comprobamos que en el procedimiento numérico, la energía se mantiene aproximadamente constante

>> Energia=x(:,2).^2*R^2/2-w^2*R^2*sin(x(:,1)).^2/2+9.8*R*(1-cos(x(:,1)))
Energia =
   -3.6750
   -3.6750
....
   -3.6414
   -3.6403

2. Cuando la energía total es positiva, E>0, para ω²>g/R (λ<1) y para ω²<g/R (λ>1). La partícula se mueve en el intervalo (-θ₀, θ₀)

El coeficiente a es negativo, el cuadrado de x₁ es negativo

${\displaystyle a{x}^4+b{x}^2+c=(-a)\left(x_0^2-x^2\right)\left(x^2+x_1^2\right),x_1^2>0}$

Buscamos la integral en la Tabla, página 282, 3.152, n° 4

${\displaystyle \begin{array}{l}{\displaystyle \underset{u}{\overset{b}{\int }}\frac{dx}{\sqrt{\left(b^2-x^2\right)\left(x^2+a^2\right)}}}=\frac{1}{\sqrt{a^2+b^2}}F\left(\delta ,r\right),\{\begin{array}{l}\delta =\arccos \frac{u}{b}\\ r=\frac{b}{\sqrt{a^2+b^2}}\end{array}\\ b>u\ge 0\end{array}}$

El resultado de la integral es

${\displaystyle \begin{array}{l}\omega t=\frac{2}{\sqrt{-a}}{\displaystyle \underset{x_0}{\overset{x}{\int }}\frac{dx}{\sqrt{\left(x_0^2-x^2\right)\left(x^2+x_1^2\right)}}}\\ \omega t=\frac{2}{\sqrt{-a}\sqrt{x_0^2+x_1^2}}F\left(\arccos \left(\frac{x}{x_0}\right),\frac{x_0}{\sqrt{x_0^2+x_1^2}}\right)\end{array}}$

Despejamos la variable x, véase la página Integrales elípticas

${\displaystyle \begin{array}{l}\text{sn}\left(\frac{\sqrt{x_0^2+x_1^2}\sqrt{-a}}{2}\omega t,\frac{x_0}{\sqrt{x_0^2+x_1^2}}\right)=\sin \left(\arccos \left(\frac{x}{x_0}\right)\right)\\ \text{sn}\left(\frac{\sqrt{x_0^2+x_1^2}\sqrt{-a}}{2}\omega t,\frac{x_0}{\sqrt{x_0^2+x_1^2}}\right)=\sqrt{1-{\left(\frac{x}{x_0}\right)}^2}\\ x=x_0\sqrt{1-{\text{sn}}^2\left(\frac{\sqrt{x_0^2+x_1^2}\sqrt{-a}}{2}\omega t,\frac{x_1}{\sqrt{x_0^2+x_1^2}}\right)}=x_0\text{cn}\left(\frac{\sqrt{x_0^2+x_1^2}\sqrt{-a}}{2}\omega t,\frac{x_1}{\sqrt{x_0^2+x_1^2}}\right)\end{array}}$

Hemos utilizado la propiedad, sn²(x|k)+cn²(x|k)=1. Dehacemos el cambio de variable x=tan(θ/2)

${\displaystyle \theta (t)=2\arctan \left(x_0\text{cn}\left(\frac{\sqrt{x_0^2+x_1^2}\sqrt{-a}}{2}\omega t,\frac{x_1}{\sqrt{x_0^2+x_1^2}}\right)\right)}$

Ejemplo: λ<1, E>0

• Velocidad angular de rotación, ω=7.0 rad/s
• Radio de la pista circular, R=1.0 m
• Posición angular inicial, θ₀=150º

La partícula se mueve entre las posciones angulares θ₀=150° (de partida) y θ₁=-150°

w=7; %velocidad angular de rotación
R=1; %radio de la pista circular
th_0=5*pi/6; %ángulo inicial, 150º, parte del reposo
E=9.8*R*(1-cos(th_0))-w^2*R^2*sin(th_0).^2/2; %energía constante
C=2*(E-9.8*R)/(R*w)^2+1; %constantes
lambda=9.8/(R*w^2); 
a=C-1-2*lambda;
%th_1=acos(lambda+sqrt(lambda^2+C));
%th_0=acos(lambda-sqrt(lambda^2+C));
x0=(1+C+2*sqrt(lambda^2+C))/(1+2*lambda-C); %cuadrado de x_0
x1=(1+C-2*sqrt(lambda^2+C))/(1+2*lambda-C); %cuadrado de x_1
x1=abs(x1);
hold on
t=linspace(0,5,200);
[~,cn,~]=ellipj(sqrt(x0+x1)*sqrt(-a)*w*t/2,x0/(x0+x1));
th=2*atan(sqrt(x0)*cn);
plot(t,th)

%solución numérica
f=@(t,x) [x(2); (w^2*cos(x(1))-9.8/R)*sin(x(1))]; 
[t,x]=ode45(f,[0,5],[th_0,0]);
plot(t,x(:,1))
hold off
grid on
xlabel('t')
ylabel('\theta')
legend('analítica','numérica','Location', 'best')
set(gca,'YTick',-pi:pi/6:pi)
set(gca,'YTickLabel',{'-\pi', '-5\pi/6', '-2\pi/3', '-\pi/2', '-\pi/3',
 '-\pi/6', '0','\pi/6','\pi/3','\pi/2','2\pi/3', '5\pi/6', '\pi'})
title('Pista circular que gira')



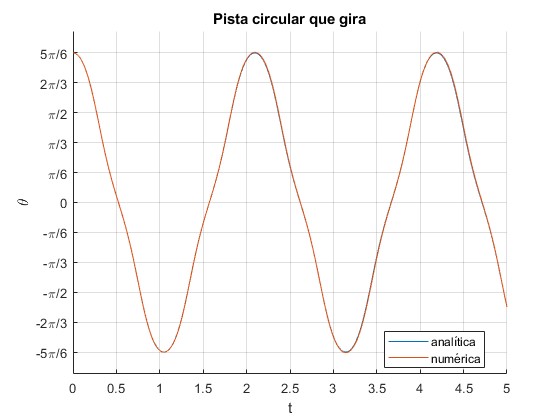
Vemos que la soluciones analítica y numérica, utilizando el procedimiento ode45 de MATLAB, prácticamente coinciden

Comprobamos que en el procedimiento numérico, la energía se mantiene aproximadamente constante

>> Energia=x(:,2).^2*R^2/2-w^2*R^2*sin(x(:,1)).^2/2+9.8*R*(1-cos(x(:,1)))
Energia =
   12.1620
   12.1620
....
   12.5429
   12.5406

Ejemplo: λ>1

• Velocidad angular de rotación, ω=2.0 rad/s
• Radio de la pista circular, R=1.0 m
• Posición angular inicial, θ₀=120º

La partícula se mueve entre las posciones angulares θ₀=120° (de partida) y θ₁=-120°



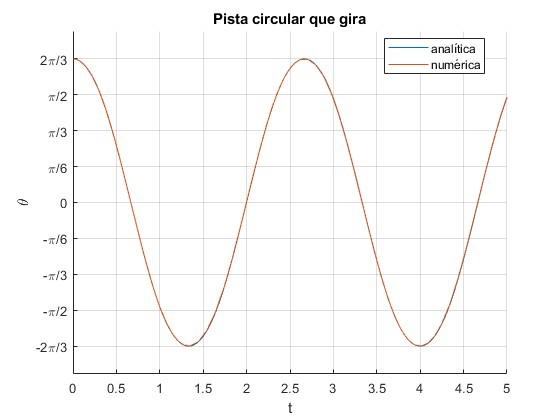
Vemos que la soluciones analítica y numérica, utilizando el procedimiento ode45 de MATLAB, prácticamente coinciden

Caso particular, E=0, ω²>g/R (λ<1)

Un caso particular importante se produce cuando la energía E de la partícula es nula, en el caso ω²>g/R (λ<1)

${\displaystyle \begin{array}{l}E=mgR\left(1-\cos \theta \right)-\frac{1}{2}m{\omega }^2{R}^2{\sin }^2\theta ,E=0\\ {\cos }^2\theta -2\lambda \cos \theta -C=0\\ \cos {\theta }_{\mathrm{0,1}}=\lambda \pm \sqrt{{\lambda }^2+C},\{\begin{array}{l}\lambda =\frac{g}{R{\omega }^2}\\ C=\frac{2\left(0-mgR\right)}{m{R}^2{\omega }^2}+1=-2\lambda +1\end{array}\\ \cos {\theta }_0=\lambda -\sqrt{{\lambda }^2+C}=2\lambda -1\\ \cos {\theta }_1=\lambda +\sqrt{{\lambda }^2+C}=\mathrm{1,}{\theta }_1=0\\ x_0^2=\frac{1-\cos {\theta }_0}{1+\cos {\theta }_0}=\frac{1-\lambda }{\lambda }\end{array}}$

w=7; %velocidad angular de rotación
R=1; %radio de la pista circular
Ep=@(x) 9.8*R*(1-cos(x))-w^2*R^2*sin(x).^2/2;
fplot(Ep,[-pi,pi])
E=0;  %energía constante
line([-pi,pi],[E,E])
lambda=9.8/(R*w^2); 
th_0=acos(2*lambda-1);
Emin=9.8*R-9.8^2/(2*w^2)-w^2*R^2/2;
line([0,0],[Emin, E], 'lineStyle', '--')
line([th_0,th_0],[Emin, E], 'lineStyle', '--')
grid on
xlabel('\theta')
ylabel('E_p(\theta)')
title('Pista circular')

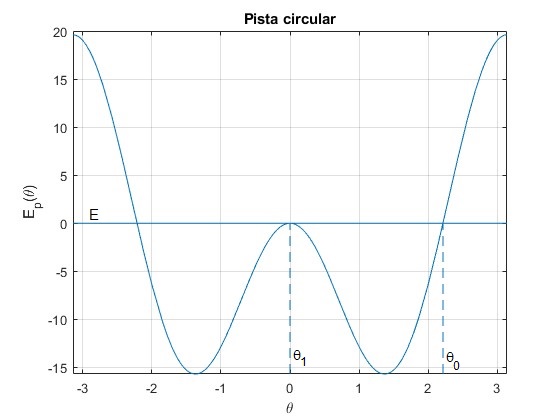
Para la energía E=0, el ángulo inicial θ₀=127°

>> th_0*180/pi
ans =
  126.8699

Resolvemos la integral, haciendo el cambio devariable x=tan(θ/2)

${\displaystyle \begin{array}{l}{\displaystyle \int \frac{d\theta }{\sqrt{C-{\cos }^2\theta +2\lambda \cos \theta }}=}{\displaystyle \int \frac{2dx}{\sqrt{a{x}^4+b{x}^2+c}}=,}\{\begin{array}{l}a=C-1-2\lambda =-4\lambda \\ b=2C+2=4-4\lambda \\ c=C-1+2\lambda =0\end{array}\\ {\displaystyle \int \frac{dx}{x\sqrt{-\lambda x^2+1-\lambda }},\lambda <1}\end{array}}$

Buscamos la integral en la Tabla, página 97, 2.266, caso (a>0, Δ<0)

${\displaystyle \begin{array}{l}{\displaystyle \int \frac{dx}{x\sqrt{c{x}^2+bx+a}}},\{\begin{array}{l}c=-\lambda <0\\ b=0\\ a=1-\lambda >0\\ \Delta =4ac-b^2=-4\lambda \left(1-\lambda \right)<0\end{array}\\ \frac{1}{\sqrt{a}}\text{arccosh}\left(\frac{2a+bx}{x\sqrt{-\Delta }}\right)=\frac{1}{\sqrt{1-\lambda }}\text{arccosh}\left(\frac{1}{x}\sqrt{\frac{1-\lambda }{\lambda }}\right)\end{array}}$

Desahaciendo el cambio de variable

${\displaystyle \begin{array}{l}\omega t=\frac{1}{\sqrt{1-\lambda }}\text{arccosh}\left(\frac{1}{x}\sqrt{\frac{1-\lambda }{\lambda }}\right)-\frac{1}{\sqrt{1-\lambda }}\text{arccosh}\left(\frac{1}{x_0}\sqrt{\frac{1-\lambda }{\lambda }}\right)\\ \omega t=\frac{1}{\sqrt{1-\lambda }}\text{arccosh}\left(\frac{1}{x}\sqrt{\frac{1-\lambda }{\lambda }}\right)\\ \cosh \left(\omega t\sqrt{1-\lambda }\right)=\frac{1}{x}\sqrt{\frac{1-\lambda }{\lambda }}\\ x=\sqrt{\frac{1-\lambda }{\lambda }}\frac{1}{\cosh \left(\omega t\sqrt{1-\lambda }\right)}\\ \theta (t)=2\arctan \left(\sqrt{\frac{1-\lambda }{\lambda }}\frac{1}{\cosh \left(\omega t\sqrt{1-\lambda }\right)}\right)\end{array}}$

Ejemplo.

• Velocidad angular de rotación, ω=7.0 rad/s
• Radio de la pista circular, R=1.0 m
• Energía E=0. Posición angular inicial, θ₀=127º

w=7; %velocidad angular de rotación
R=1; %radio de la pista circular
E=0; %energía constante
%solución numérica
f=@(t,x) [x(2); (w^2*cos(x(1))-9.8/R)*sin(x(1))]; 
[t,x]=ode45(f,[0,5],[th_0,0]);
hold on
plot(t,x(:,1))
%solución analítica
C=2*(E-9.8*R)/(R*w)^2+1; %constantes
lambda=9.8/(R*w^2); 
th_0=acos(lambda-sqrt(lambda^2+C));
x0=(1+C+2*sqrt(lambda^2+C))/(1+2*lambda-C); %cuadrado de x_0
th=@(t) 2*atan(sqrt((1-lambda)/lambda)./cosh(sqrt(1-lambda)*(w*t)));
fplot(th,[0,5])
hold off
grid on
xlabel('t')
ylabel('\theta')
legend('numérica', 'analítica','Location', 'best')
set(gca,'YTick',0:pi/6:pi)
set(gca,'YTickLabel',{'0','\pi/6','\pi/3','\pi/2','2\pi/3', '5\pi/6', '\pi'})
title('Pista circular que gira')

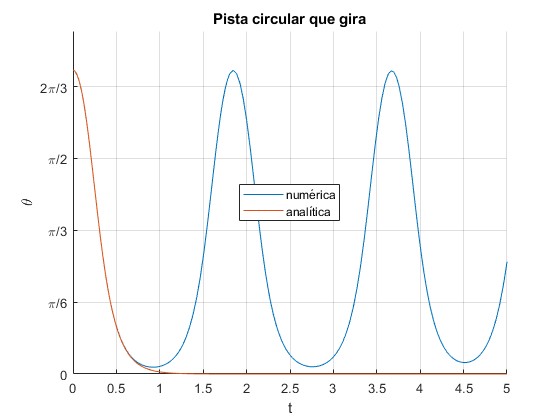
En la solución analítica, la partícula parte de la posición θ₀=127° y tiende a la posición θ₁=0, que alcanza después de un tiempo infinito. Esta posición es de equilibrio inestable, cualquier perturbación, por pequeña que sea, hace que la partícula regrese a la posición de partida.

Comprobamos que en el procedimiento numérico, la energía se mantiene aproximadamente constante

>> Energia=x(:,2).^2*R^2/2-w^2*R^2*sin(x(:,1)).^2/2+9.8*R*(1-cos(x(:,1)))
Energia =
    0.0000
    0.0000
    ....
    -0.1305
    -0.1304

Resumen: ω²>g/R (λ<1)

La situación más importante se produce para ω²>g/R (λ<1). Por ejemplo: la velocidad angular de rotación, ω=7.0 rad/s, radio de la pista circular, R=1.0 m

Representamos en el mismo script, la posición angular θ(t) de la partícula para tres valores de la energía

• E<0
• E=0
• E>0

w=7; %velocidad angular de rotación
R=1; %radio de la pista circular
hold on
for E=[-5,0,5]
    C=2*(E-9.8*R)/(R*w)^2+1; %constantes
    lambda=9.8/(R*w^2); 
%     th_1=acos(lambda+sqrt(lambda^2+C)); %ángulos extremos
%     th_0=acos(lambda-sqrt(lambda^2+C));
    x0=(1+C+2*sqrt(lambda^2+C))/(1+2*lambda-C); %cuadrado de x_0
    x1=(1+C-2*sqrt(lambda^2+C))/(1+2*lambda-C); %cuadrado de x_1
    if E<0
        a=C-1-2*lambda; %coeficiente
        th=@(t) 2*atan(sqrt(x1)./sqrt(1-(1-x1/x0)*ellipj(sqrt(x0)*
sqrt(-a)*w*t/2,1-x1/x0).^2));
        fplot(th,[0,5],'displayName',num2str(E))
    elseif E>0
        x1=abs(x1);
        t=linspace(0,5,200);
        [~,cn,~]=ellipj(sqrt(x0+x1)*sqrt(-a)*w*t/2,x0/(x0+x1));
        th=2*atan(sqrt(x0)*cn);
        plot(t, th, 'displayName',num2str(E))
    else
        th=@(t) 2*atan(sqrt((1-lambda)/lambda)./cosh(sqrt(1-lambda)*(w*t)));
        fplot(th,[0,5],'displayName',num2str(E))
    end
end
hold off
grid on
xlabel('t')
legend('-DynamicLegend','location','northeast')
ylabel('\theta')
set(gca,'YTick',-pi:pi/6:pi)
set(gca,'YTickLabel',{'-\pi', '-5\pi/6', '-2\pi/3', '-\pi/2', '-\pi/3', 
'-\pi/6', '0','\pi/6','\pi/3','\pi/2','2\pi/3', '5\pi/6', '\pi'})
title('Pista circular que gira')

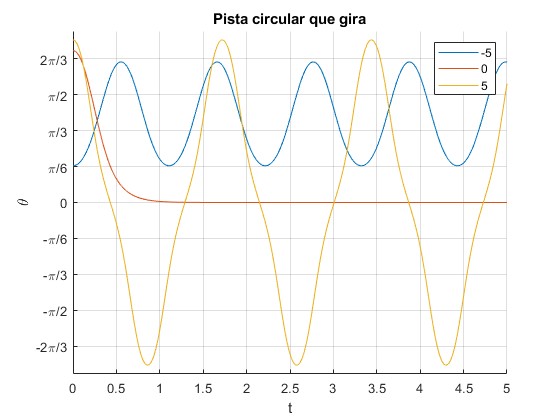
Con rozamiento

Supongamos que el coeficiente de rozamiento entre la partícula y la superficie circular sobre la que desliza es μ_s. La partícula permanecerá en reposo si F_r/N<μ_s

La reacción N de la superficie circular es

N=mgcosθ+F_csinθ=mgcosθ+mω²R·sin²θ

La reacción N se anula para el ángulo

${\displaystyle \begin{array}{l}g\cos \theta +{\omega }^{2}R\left(1-{\cos }^2\theta \right)=0\\ {\cos }^2\theta -\frac{g}{{\omega }^{2}R}\cos \theta -1=0\\ \cos \theta =\frac{1}{2}\left(\frac{g}{{\omega }^{2}R}-\sqrt{{\left(\frac{g}{{\omega }^{2}R}\right)}^2+4}\right)\end{array}}$

Representamos N/mg en función de θ para dos velocidades angulares de rotación ω=2, 7 rad/s

R=1; %radio
hold on
for w=[2,7] %velocidad angular de rotación
    f=@(x) cos(x)+w^2*R*sin(x).^2/9.8;
    th=acos((9.8/(w^2*R)-sqrt((9.8/(w^2*R))^2+4))/2);
    fplot(f,[0,th],'displayName',num2str(w))
    disp(th*180/pi)
end
hold off
grid on
set(gca,'XTick',0:pi/6:pi)
set(gca,'XTickLabel',{'0','\pi/6','\pi/3','\pi/2','\pi/3',
'2\pi/3','5\pi/6','\pi'})
legend('-DynamicLegend','location','best')
xlabel('\theta')
ylabel('N/mg')
title('Pista con rozamiento'

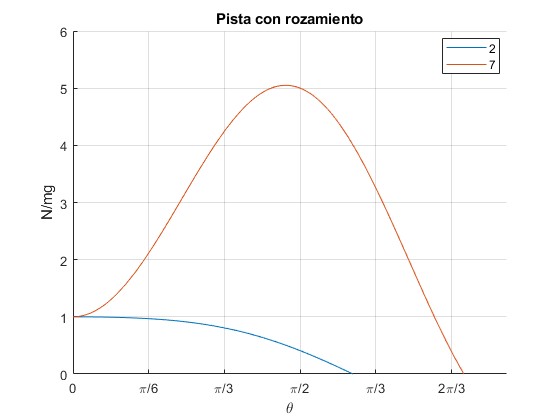
Los posiciones angulares para las cuales la reacción N de la pista se anula son, 110.9° y 154.8°, respectivamente

  110.8754
  154.8216

ω²<g/R

La posición de equilibrio estable es θ_e=0

Para θ>0, la componente tangencial del peso mgsinθ es mayor que la componente tangencial de la fuerza centrífuga, F_ccosθ=mω²Rsinθ·cosθ. La fuerza de rozamiento es la diferencia F_r= mgsinθ-F_ccosθ

Representamos F_r/N en función de θ para ω=2 rad/s, con R=1.0 m.

${\displaystyle \frac{F_r}{N}=\frac{g\sin \theta -{\omega }^{2}R\sin \theta ·\cos \theta }{g\cos \theta +{\omega }^{2}R{\sin }^2\theta }=\frac{\left(g-{\omega }^{2}R\cos \theta \right)\sin \theta }{g\cos \theta +{\omega }^{2}R{\sin }^2\theta }}$

R=1; %radio
w=2; %velocidad angular de rotación
f=@(x) (9.8*sin(x)-w^2*R*sin(x).*cos(x))./(9.8*cos(x)+w^2*R*sin(x).^2);
fplot(f,[0,pi/3])
mu=0.4; %coeficiente estático
g=@(x) 9.8*sin(x)-w^2*R*sin(x)*cos(x)-mu*(9.8*cos(x)+w^2*R*sin(x)^2);
th_1=fzero(g,[0,pi/3]);
line([th_1,th_1],[0,mu],'lineStyle','--')
line([0,th_1],[mu,mu],'lineStyle','--')
grid on
set(gca,'XTick',0:pi/12:pi/3)
set(gca,'XTickLabel',{'0','\pi/12','\pi/6','\pi/4','\pi/3'})
xlabel('\theta')
ylabel('F_r/N')
title('Pista con rozamiento')

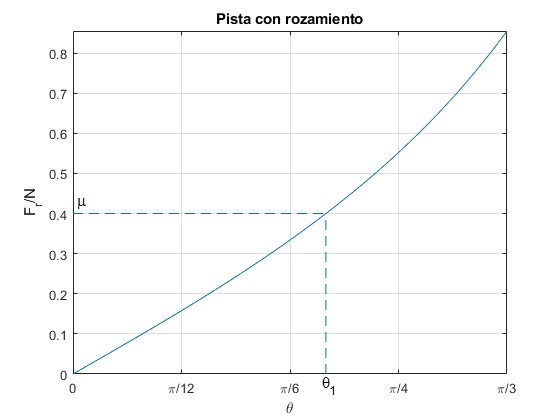
Dado el coeficiente de rozamiento μ_s, las posiciones θ en las que la partícula está en equilibrio serán aquellas para las que F_r/N<μ_s, es decir θ<θ₁

El ángulo θ₁ se calcula resolviendo la ecuación trascendente, F_r=μ_sN, utilizando la función fzero de MATLAB

${\displaystyle g\sin \theta -{\omega }^{2}R\sin \theta ·\cos \theta =\mu \left(g\cos \theta +{\omega }^{2}R{\sin }^2\theta \right)}$

El ángulo θ₁ en grados es

>> th_1*180/pi
ans =   34.9675

Si la posición inicial de la partícula θ₀>θ₁ la partícula desliza hacia abajo, la velocidad angular es negativa dθ/dt<0. Las fuerzas sobre la partícula se han mostrado en la figura más arriba. La ecuación del movimiento es

${\displaystyle \begin{array}{l}mR\frac{d^2\theta }{d{t}^2}=F_c\cos \theta -mg\sin \theta +F_r\\ F_r=\mu N=\mu (F_c\sin \theta +mg\cos \theta )\\ \frac{d^2\theta }{d{t}^2}=\left({\omega }^2\cos \theta -\frac{g}{R}\right)\sin \theta +\mu \left({\omega }^2{\sin }^2\theta +\frac{g}{R}\cos \theta \right)\end{array}}$

Se resuelve esta ecuación diferencial por procedimientos numéricos, con las siguientes condiciones iniciales, en el instante t=0, θ=θ₀, dθ/dt=0.

Supongamos que el coeficiente cinético de la pista es μ_s=μ_k=0.4 y la partícula parte en reposo desde la posición θ₀=π/3 (60°) que es mayor que θ₁

function pista_1
    R=1; %radio
    w=2; %velocidad angular de rotación
    mu=0.4; %coeficiente estático y cinético
    f=@(t,x) [x(2); (w^2*cos(x(1))-9.8/R)*sin(x(1))+mu*(w^2*sin(x(1))^2
+9.8*cos(x(1))/R)]; 
    opts=odeset('events',@stop_pista);
    [t,x]=ode45(f,[0,10],[pi/3,0], opts);
    plot(t,x(:,1)) %tiempo, posición
    grid on
    set(gca,'YTick',0:pi/12:pi/2)
    set(gca,'YTickLabel',{'0','\pi/12','\pi/6','\pi/4','\pi/3', '5\pi/12',
'\pi/2'})
    xlabel('t')
    ylabel('\theta');
    title('Pista con rozamiento')
 
    th=x(end,1);
    disp([t(end), th*180/pi])
    N=w^2*R*sin(th)^2+9.8*cos(th);
    Fr=9.8*sin(th)-w^2*R*sin(th)*cos(th);
    disp([Fr, mu*N])

    function [value,isterminal,direction]=stop_pista(~,x)
        value=x(2);
        isterminal=1; %1 detiene cuando la velocidad se hace cero   
        direction=1; 
    end
end

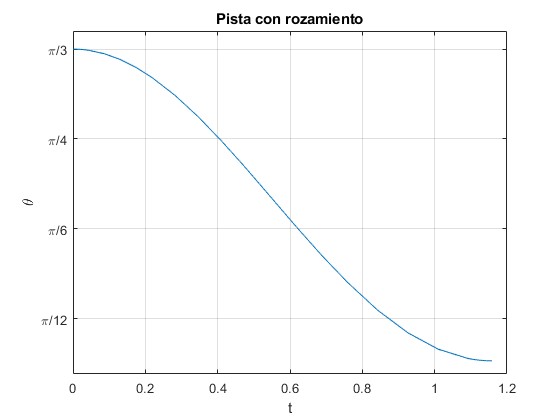
Cuando la partícula se detiene, se verifica si |F_r/N|<μ_s en cuyo caso la partícula permanece en reposo, en caso contrario, continua su movimiento hasta la próxima posición de parada.

    1.1585    7.9277
    0.8052    3.9130

La partícula se detiene en la posición θ=7.93° empleando un tiempo de t=1.16 s.

En la posición en la que se detiene, la fuerza de rozamiento vale F_r=0.8052 que es menor que la máxima μ_sN=3.9130 N

ω²>g/R

Representamos F_r/N en función de θ para ω=7 rad/s, con R=1.0 m.

R=1; %radio
w=7; %velocidad angular de rotación
f=@(x) (9.8*sin(x)-w^2*R*sin(x).*cos(x))./(9.8*cos(x)+w^2*R*sin(x).^2);
hold on
fplot(f,[0,2*pi/3])
mu=0.4; %coeficiente estático
g=@(x) 9.8*sin(x)-w^2*R*sin(x)*cos(x)-mu*(9.8*cos(x)+w^2*R*sin(x)^2);
th_3=fzero(g,[0,2*pi/3]);
line([th_3,th_3],[0,mu],'lineStyle','--')
line([0,th_3],[mu,mu],'lineStyle','--')
%equilibrio
th_e=acos(9.8/(w^2*R));
plot(th_e,0,'ro','markersize',4,'markerfacecolor','r')
%mínimo
th_m=acos((-9.8+sqrt(9.8^2+4*(9.8^2+w^4*R^2)))/(2*w^2*R));
mu=-0.4; %coeficiente estático
g=@(x) 9.8*sin(x)-w^2*R*sin(x)*cos(x)-mu*(9.8*cos(x)+w^2*R*sin(x)^2);
th_1=fzero(g,[0,th_m]);
line([th_1,th_1],[0,mu],'lineStyle','--')
line([0,th_1],[mu,mu],'lineStyle','--')
th_2=fzero(g,[th_m, th_e]);
line([th_2,th_2],[0,mu],'lineStyle','--')
line([0,th_2],[mu,mu],'lineStyle','--')
hold off
disp([th_1, th_2, th_e, th_3]*180/pi)
grid on
xlim([0,2*pi/3])
set(gca,'XTick',0:pi/12:2*pi/3)
set(gca,'XTickLabel',{'0','\pi/12','\pi/6','\pi/4','\pi/3', '5\pi/12',
 '\pi/2', '7\pi/12','2\pi/3'})
xlabel('\theta')
ylabel('F_r/N')
title('Pista con rozamiento')

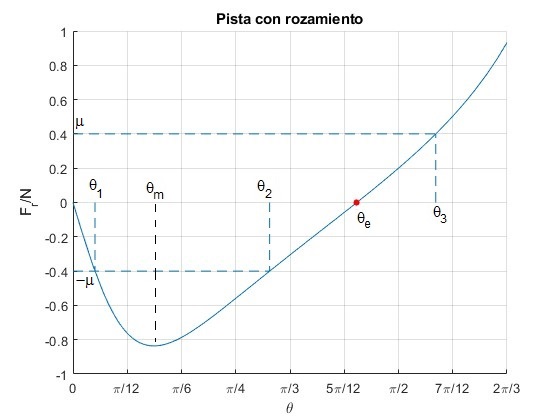
La fuerza de rozamiento es nula en la posición de equilibrio estable ${\theta }_e=\arccos \left(\frac{g}{{\omega }^{2}R}\right)$, se señala mediante un punto de color rojo en la figura, θ_e=78.46°

Observamos en la representación gráfica un mínimo en la posición θ_m, que se calcula derivando F_r/N respecto de θ e igualando a cero

${\displaystyle \begin{array}{l}\frac{d}{d\theta }\left(\frac{F_r}{N}\right)=\frac{\left(\left(g-{\omega }^{2}R\cos \theta \right)\cos \theta +{\omega }^{2}R{\sin }^2\theta \right)\left(g\cos \theta +{\omega }^{2}R{\sin }^2\theta \right)-\left(-g\sin \theta +2{\omega }^{2}R\sin \theta \cos \theta \right)\left(g-{\omega }^{2}R\cos \theta \right)\sin \theta }{{\left(g\cos \theta +{\omega }^{2}R{\sin }^2\theta \right)}^2}=\\ \frac{g^2+{\omega }^4{R}^2{\sin }^2\theta -g{\omega }^{2}R\cos \theta }{{\left(g\cos \theta +{\omega }^{2}R{\sin }^2\theta \right)}^2}=0\\ {\omega }^4{R}^2{\cos }^2\theta +g{\omega }^{2}R\cos \theta -\left(g^2+{\omega }^4{R}^2\right)=0\\ {\theta }_m=\arccos \left(\frac{-g+\sqrt{g^2+4\left(g^2+{\omega }^4{R}^2\right)}}{2{\omega }^{2}R}\right)\end{array}}$

Los ángulos límites θ₁ y θ₂ o θ₃ para un valor dado del coeficiente de rozamiento μ_s y una determinada velocidad angular ω se calculan utilizando la función fzero de MATLAB para resolver la ecuación trascendente, F_r=μ_sN

|gsinθ-ω²Rsinθcosθ|=μ(gcosθ+ω²Rsin²θ)

   6.0718   54.3757   78.4630  100.3107

• Para θ>θ_e

La componente tangencial del peso mgsinθ es mayor que la componente tangencial de la fuerza centrífuga, F_ccosθ. La fuerza de rozamiento es la diferencia F_r= mgsinθ-F_ccosθ

Dado el coeficiente de rozamiento μ_s=0.4, las posiciones θ para las cuales la partícula está en equilibrio serán aquellas para las que F_r/N<μ, es decir θ_e≤θ<θ₃.

Si la posición inicial de la partícula θ₀>θ₃, (θ₃=100.31°), la partícula desliza hacia abajo, la velocidad angular es negativa dθ/dt<0. Las fuerzas sobre la partícula se muestran en la figura más arriba en el caso anterior. La ecuación del movimiento es la misma

${\displaystyle \frac{d^2\theta }{d{t}^2}=\left({\omega }^2\cos \theta -\frac{g}{R}\right)\sin \theta +\mu \left({\omega }^2{\sin }^2\theta +\frac{g}{R}\cos \theta \right)}$

Supongamos que el coeficiente cinético de la pista es μ_s=μ_k=0.4 y la partícula parte en reposo desde la posición θ₀=2π/3 (120°) que es mayor que θ₃

function pista_2
    R=1; %radio
    w=7; %velocidad angular de rotación
    mu=0.4; %coeficiente estático y cinético
    f=@(t,x) [x(2); (w^2*cos(x(1))-9.8/R)*sin(x(1))+
mu*(w^2*sin(x(1))^2+9.8*cos(x(1))/R)]; 
    opts=odeset('events',@stop_pista);
    [t,x]=ode45(f,[0,10],[2*pi/3,0], opts);
    plot(t,x(:,1)) %tiempo, posición
    set(gca,'YTick',0:pi/12:2*pi/3)
    set(gca,'YTickLabel',{'0','\pi/12','\pi/6','\pi/4','\pi/3', 
'5\pi/12','\pi/2', '7\pi/12','2\pi/3'})
    xlabel('t')
    ylabel('\theta');
    title('Pista con rozamiento')
    grid on

    th=x(end,1);
    disp([t(end), th*180/pi])
    N=w^2*R*sin(th)^2+9.8*cos(th);
    Fr=9.8*sin(th)-w^2*R*sin(th)*cos(th);
    disp([Fr, mu*N])


    function [value,isterminal,direction]=stop_pista(~,x)
       %x(1) es  x, x(3) es y
        value=x(2);
        isterminal=1; %1 detiene cuando la velocidad se hace cero   
        direction=1; 
    end
end

    0.4364   80.9782
    2.0901   19.7327

La partícula se detiene en la posición θ=81.0° empleando un tiempo de t=0.44 s.

En la posición en la que se detiene, la fuerza de rozamiento vale F_r=2.0901 que es menor que la máxima μ_sN=19.7327 N

• Para θ<θ_e

La componente tangencial del peso mgsinθ es menor que la componente tangencial de la fuerza centrífuga, F_ccosθ. La fuerza de rozamiento es la diferencia

F_r= F_ccosθ- mgsinθ

En la figura anterior F_r/N en función de θ para θ<θ_e aparece cambiada de signo.

Dado el coeficiente de rozamiento μ_s=0.4, las posiciones θ para las cuales la partícula está en equilibrio serán aquellas para las que |F_r/N|<μ_s, es decir 0≤θ<θ₁ (θ₁=6.07°) y θ₂<θ≤θ_e (θ₂=54.38° y θ_e=78.46°)

Si la posición inicial de la partícula está en el intervalo θ₁≤θ₀≤ θ₂ la partícula desliza hacia arriba, la velocidad angular es positiva dθ/dt>0. Las fuerzas sobre la partícula se muestran en la figura.

La ecuación del movimiento es

${\displaystyle \begin{array}{l}mR\frac{d^2\theta }{d{t}^2}=F_c\cos \theta -mg\sin \theta -F_r\\ \frac{d^2\theta }{d{t}^2}=\left({\omega }^2\cos \theta -\frac{g}{R}\right)\sin \theta -\mu \left({\omega }^2{\sin }^2\theta +\frac{g}{R}\cos \theta \right)\end{array}}$

Supongamos que el coeficiente cinético de la pista es μ_s=μ_k=0.4 y la partícula parte en reposo desde la posición θ₀=π/6 (30°) que es mayor que θ₁ y menor que θ₂

function pista_4
    R=1; %radio
    w=7; %velocidad angular de rotación
    mu=0.4; %coeficiente estático y cinético
    f=@(t,x) [x(2); (w^2*cos(x(1))-9.8/R)*sin(x(1))-mu*(w^2*sin(x(1))^2+
9.8*cos(x(1))/R)]; 
    opts=odeset('events',@stop_pista);
    [t,x]=ode45(f,[0,10],[pi/6,0], opts);
    plot(t,x(:,1)) %tiempo, posición
    set(gca,'YTick',0:pi/12:pi/2)
    set(gca,'YTickLabel',{'0','\pi/12','\pi/6','\pi/4','\pi/3',
 '5\pi/12','\pi/2'})
    xlabel('t')
    ylabel('\theta');
    title('Pista con rozamiento')
    grid on

    th=x(end,1);
    disp([t(end), th*180/pi])
    N=w^2*R*sin(th)^2+9.8*cos(th);
    Fr=9.8*sin(th)-w^2*R*sin(th)*cos(th);
    disp([Fr, mu*N])


    function [value,isterminal,direction]=stop_pista(~,x)
       %x(1) es  x, x(3) es y
        value=x(2);
        isterminal=1; %1 detiene cuando la velocidad se hace cero   
        direction=-1; 
    end
end

    0.5736   73.0992
   -4.2531   19.0831

La partícula se detiene en la posición θ=73.1° empleando un tiempo de t=0.57 s.

En la posición en la que se detiene, la fuerza de rozamiento vale F_r=4.25 que es menor que la máxima μ_sN=19.08 N

Actividades

Se introduce

• La posición angular inicial θ₀, en el control titulado Posición angular inicial.
• La velocidad angular de rotación ω, en el control titulado Velocidad angular.
• El coeficiente de rozamiento μ, en el control titulado Coeficiente rozamiento.
• El radio de la pista circular se ha fijado en R=1.0 m

Se pulsa el botón titulado Nuevo

Observamos el movimiento de la partícula en equlibrio o deslizando a lo largo de la pista circular, tal como lo vería un observador no inercial que girase con la pista circular. Se marca la posición angular de equilibrio estable θ_e.

En la parte derecha, se representa la curva de energía potencial E_p(θ) en color azul, la energía total E (un segmento de color negro). La partícula oscila alrededor de las posiciones de equilibrio θ_e entre las posiciones de retorno, una es la posición inicial θ₀ y la otra la raíz de la ecuación E_p(θ)=E_p(θ₀).

Referencias

Thomas E. Baker, Andreas Bill. Jacobi elliptic functions and the complete solution to the bead on the hoop problem. Am. J. Phys. 80 (6), June 2012. pp. 506-514

I. S. Gradshteyn, I. M. Ryzhik. Table of Integrals, Series, and Products. Seventh Edition. Elsevier (2007). Integrales: (primera solución) pág. 282, 3.152, n° 9, (segunda solución) pág. 282, 3.152, n° 4, (tercera solución) pág. 97, 2.266, caso (a>0, Δ<0)