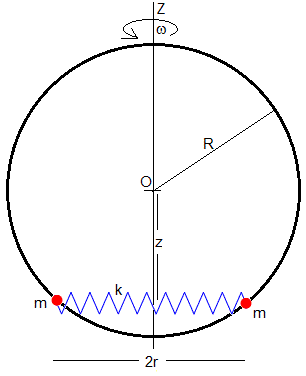
En la figura, se muestra un sistema formado por dos partículas de masa m unidas por un muelle elástico de constante k que pueden deslizar a lo largo de un aro de radio R cuyo eje horizontal de giro Z pasa por un diámetro.

La velocidad angular de rotación ω es constante.

En la página titulada Vibración de una molécula diatómica. El potencial de Lennard-Jones, calculamos la frecuencia angular de vibración de dos partículas de masas m₁ y m₂ unidas por un muelle elástico de constante k

${\displaystyle \omega =\sqrt{\frac{k}{\mu }},\mu =\frac{m_1{m}_2}{m_1+m_2}}$

Donde μ=m/2 es la masa reducida

${\displaystyle {\omega }_0=\sqrt{2\frac{k}{m}}}$

Como el eje de giro Z es horizontal, el centro de masa de las dos partículas está en dicho eje por tanto, no hay cambio en la energía potencial gravitatoria. La energía potencial se debe únicamente a la deformación del muelle elástico

${\displaystyle E_p=\frac{1}{2}k{\left(2r-2r_0\right)}^2=2k{\left(r-r_0\right)}^2}$

2r₀ (r₀<R) es la longitud del muelle sin deformar. La energía cinética es

${\displaystyle E_k=2\frac{1}{2}m\left({\left(\frac{dr}{dt}\right)}^2+r^2{\omega }^2+{\left(\frac{dz}{dt}\right)}^2\right)=m\left({\left(\frac{dr}{dt}\right)}^2+r^2{\omega }^2+{\left(\frac{dz}{dt}\right)}^2\right)}$

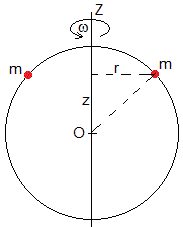
Siendo r la distancia de la partícula al eje de rotación Z y z es la distancia al origen de la recta que une a las dos partículas. La expresión anterior es la energía cinética de una partícula en coordenadas cilíndricas, con ρ=r y dφ/dt=ω

Como las partículas deslizan a lo largo del aro, r y z están relacionados

${\displaystyle \begin{array}{l}{r}^2=R^2-z^2\\ r\frac{dr}{dt}=-z\frac{dz}{dt}\\ \frac{dr}{dt}=-\frac{z}{\sqrt{R^2-z^2}}\frac{dz}{dt}\end{array}}$

La energía cinética se expresa en términos de la variable z

${\displaystyle E_k=m\left(\frac{z^2}{R^2-z^2}{\left(\frac{dz}{dt}\right)}^2+\left(R^2-z^2\right){\omega }^2+{\left(\frac{dz}{dt}\right)}^2\right)=m\left(\frac{R^2}{R^2-z^2}{\left(\frac{dz}{dt}\right)}^2+\left(R^2-z^2\right){\omega }^2\right)}$

La lagrangiana L=E_k-E_p es

${\displaystyle \begin{array}{l}L=m\left(\frac{R^2}{R^2-z^2}{\left(\frac{dz}{dt}\right)}^2+\left(R^2-z^2\right){\omega }^2\right)-2k{\left(\sqrt{R^2-z^2}-r_0\right)}^2\\ L=m\frac{R^2}{R^2-z^2}{\left(\frac{dz}{dt}\right)}^2+m\left(R^2-z^2\right){\omega }^2-2k{\left(\sqrt{R^2-z^2}-r_0\right)}^2\\ L=\frac{1}{2}\mu {\left(\frac{dz}{dt}\right)}^2-V_e(z)\end{array}}$

Hemos definido una masa y un potencial efectivos

${\displaystyle \begin{array}{l}\mu =2m\frac{R^2}{R^2-z^2}\\ V_e(z)=2k{\left(\sqrt{R^2-z^2}-r_0\right)}^2-m{\omega }^2\left(R^2-z^2\right)\end{array}}$

El potencial efectivo es la suma de la energía potencial del muelle deformado y del potencial centrífugo

Posiciones de equilibrio

Las posiciones de equilibrio se determinan igualando la derivada primera respecto de z del potencial efectivo a cero.

${\displaystyle \begin{array}{l}\frac{d{V}_e(z)}{dz}=-4k\left(\sqrt{R^2-z^2}-r_0\right)\frac{z}{\sqrt{R^2-z^2}}+2m{\omega }^{2}z=2z\left(\frac{2k{r}_0}{\sqrt{R^2-z^2}}-2k+m{\omega }^2\right)\\ \frac{d{V}_e(z)}{dz}=4k{r}_{0}z\left(\frac{1}{\sqrt{R^2-z^2}}-\frac{1}{\xi }\right),\xi =\frac{2k{r}_0}{2k-m{\omega }^2}\end{array}}$

Existen tres posiciones de equilibrio. La primera es z=0, y las otras dos

${\displaystyle \begin{array}{l}\frac{1}{\sqrt{R^2-z^2}}=\frac{1}{\xi }\\ z=\pm \sqrt{R^2-{\xi }^2}\end{array}}$

dV_e/dz=0, tiene tres raíces reales si ξ<R y una raíz real z=0, si ξ>R.

Se denomina velocidad angular crítica ω_c a aquella que hace que ξ=R

${\displaystyle \begin{array}{l}\frac{2k{r}_0}{2k-m{\omega }^2}=R\\ {\omega }_c^2=2\frac{k}{m}\frac{R-r_0}{R}={\omega }_0^2\left(1-\epsilon \right)\end{array}}$

Hemos definido el parámetro adimensional ε=r₀/R

Si ω<ω_c, entonces ξ<R, hay tres raíces reales, y si ω>ω_c entonces ξ>R, solamente hay una raíz real z=0.

Para determinar si la posición de equilibrio es estable o inestable, evaluamos la derivada segunda

${\displaystyle \frac{d^2{V}_e(z)}{d{z}^2}=4k{r}_0\left(\frac{1}{\sqrt{R^2-z^2}}-\frac{1}{\xi }\right)+4k{r}_0\frac{z^2}{{\left(R^2-z^2\right)}^{3/2}}=4k{r}_0\left(\frac{R^2}{{\left(R^2-z^2\right)}^{3/2}}-\frac{1}{\xi }\right)}$

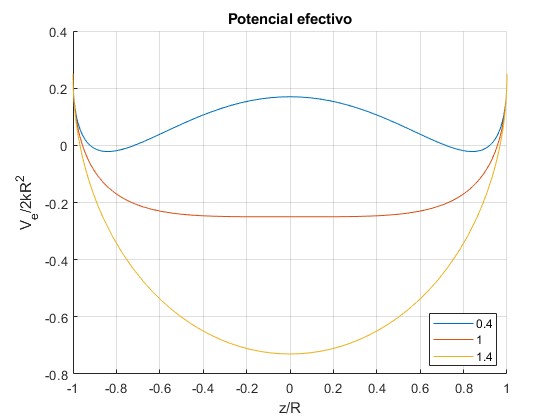
Representamos el potencial efectivo V_e(z), en términos de magnitudes adimensionales, x=z/R, ω/ω_c y ε=r₀/R

${\displaystyle \begin{array}{l}\frac{V_e(z)}{2k{R}^2}={\left(\sqrt{1-\frac{z^2}{R^2}}-\frac{r_0}{R}\right)}^2-\frac{m{\omega }^2}{2k}\left(1-\frac{z^2}{R^2}\right)\\ \frac{V_e(z)}{2k{R}^2}={\left(\sqrt{1-\frac{z^2}{R^2}}-\frac{r_0}{R}\right)}^2-\frac{{\omega }^2}{{\omega }_0^2}\left(1-\frac{z^2}{R^2}\right)\\ \frac{V_e(x)}{2k{R}^2}={\left(\sqrt{1-x^2}-\epsilon \right)}^2-\left(1-\epsilon \right)\frac{{\omega }^2}{{\omega }_c^2}\left(1-x^2\right)\end{array}}$

ex=0.5; %cociente r0/R
hold on
for W=[0.4,1,1.4]
    f=@(x) (sqrt(1-x.^2)-ex).^2-(1-ex)*W^2*(1-x.^2); %x=z/R, W=w/w_c
    fplot(f,[-1,1],'displayName',num2str(W))
end
hold off
grid on
legend('-DynamicLegend','location','best')
xlabel('z/R')
ylabel('V_e/2kR^2')
title('Potencial efectivo')

Teniendo en cuenta

${\displaystyle \begin{array}{l}{\omega }_0^2=2\frac{k}{m}\\ {\omega }_c^2={\omega }_0^2\left(1-\epsilon \right)\\ \frac{1}{\xi }=\frac{2k-m{\omega }^2}{2k{r}_0}=\frac{1}{r_0}\left(1-\frac{{\omega }^2}{{\omega }_0^2}\right)=\frac{1}{r_0}\left(1-\left(1-\epsilon \right)\frac{{\omega }^2}{{\omega }_c^2}\right)\end{array}}$

La posición de equilibrio estable x_e para ω<ω_c se expresa en términos de dichas magnitudes adimensionales

${\displaystyle \begin{array}{l}{x}_e=\frac{z_e}{R}=\pm \sqrt{1-\frac{{\xi }^2}{R^2}}\\ x_e=\pm \sqrt{1-\frac{{\epsilon }^2}{{\left(1-\left(1-\epsilon \right)\frac{{\omega }^2}{{\omega }_c^2}\right)}^2}}=\pm \frac{\sqrt{\left(1-\epsilon \right)\left(1+\epsilon +\left(1-\epsilon \right)\frac{{\omega }^4}{{\omega }_c^4}-2\frac{{\omega }^2}{{\omega }_c^2}\right)}}{\left(1-\left(1-\epsilon \right)\frac{{\omega }^2}{{\omega }_c^2}\right)}\end{array}}$

Para ε=0.5 y para ω/ω_c=0.4, la posición de equilibrio estable (mínimo) es x_e=±0.8394. Véase la sección 'Ecuación del movimiento'

Oscilaciones de pequeña amplitud

Alrededor de las posiciones de equilibrio estable las partículas oscilan. Si la amplitud es pequeña, las oscilaciones son aproximadamente armónicas. La constante efectiva del muelle es el valor de la derivada segunda del potencial efectivo evaluada en la posición de equilibrio estable z_e

Desarrollamos en serie V_e(z) alrededor de la posición de equilibrio z_e

${\displaystyle \begin{array}{l}{V}_e(z)=V_e(z_e)+{\frac{d{V}_e(z)}{dz}|}_{z_e}\left(z-z_e\right)+\frac{1}{2}{\frac{d^2{V}_e(z)}{d{z}^2}|}_{z_e}{\left(z-z_e\right)}^2+\mathrm{...}\\ V_e(z)=V_e(z_e)+\frac{1}{2}{k}_e{\left(z-z_e\right)}^2+\mathrm{...}\end{array}}$

Hay tres posibles posiciones de equilibrio estable z_e=0, y $z_e=\pm \sqrt{R^2-{\xi }^2}$, de las cuales consideramos dos, al ser una simétrica de la otra

• Para ω>ω_c, z_e=0, es la posición de equilibrio estable

La derivada segunda del potencial efectivo en la posición de equilibrio vale

${\displaystyle k_e=4k{r}_0\left(\frac{1}{R}-\frac{1}{\xi }\right)}$

La energía potencial V_e(z) efectiva en las proximidades de z_e=0 se puede aproximar y expresar en términos de magnitudes adimensionales ω/ω_c y ε=r₀/R

${\displaystyle \begin{array}{l}{V}_e(z)\approx V_e(0)+\frac{1}{2}4k{r}_0\left(\frac{1}{R}-\frac{1}{\xi }\right)z^2\\ V_e(z)\approx 2k{\left(R-r_0\right)}^2-m{\omega }^2{R}^2+2k{r}_0\left(\frac{1}{R}-\frac{1}{\xi }\right)z^2\\ \frac{V_e(z)}{2k{R}^2}\approx {\left(1-\frac{r_0}{R}\right)}^2-\frac{m}{2k}{\omega }^2+\left(\frac{r_0}{R}-\frac{r_0}{\xi }\right)\frac{z^2}{R^2}\\ \frac{V_e(z)}{2k{R}^2}\approx {\left(1-\epsilon \right)}^2-\frac{{\omega }^2}{{\omega }_0^2}+\left(\epsilon -\left(1-\frac{{\omega }^2}{{\omega }_0^2}\right)\right)\frac{z^2}{R^2}\\ \zeta =1-\frac{{\omega }^2}{{\omega }_0^2}=1-\left(1-\epsilon \right)\frac{{\omega }^2}{{\omega }_c^2}\\ \frac{V_e(x)}{2k{R}^2}\approx {\left(1-\epsilon \right)}^2-\left(1-\zeta \right)+\left(\epsilon -\zeta \right)x^2\end{array}}$

Representamos la energía potencial efectiva exacta y aproximada tomando el término constante y el primer término del desarrollo en serie, para ε=0.5 y para ω/ω_c=1.4

ex=0.5; %cociente r0/R
hold on
W=1.4; %w/w_c
f=@(x) (sqrt(1-x.^2)-ex).^2-(1-ex)*W^2*(1-x.^2); %exacto
xe=0; %equilibrio
Z=1-(1-ex)*W^2;
g=@(x) (1-ex)^2-(1-Z)+(ex-Z)*x.^2; %aproximado
fplot(f,[xe-0.1,xe+0.1])
fplot(g,[xe-0.1,xe+0.1])
hold off
grid on
xlabel('x')
legend('potencial','aproximación','location','best')
ylabel('V_e(x)')
title('Potencial efectivo y aproximación')



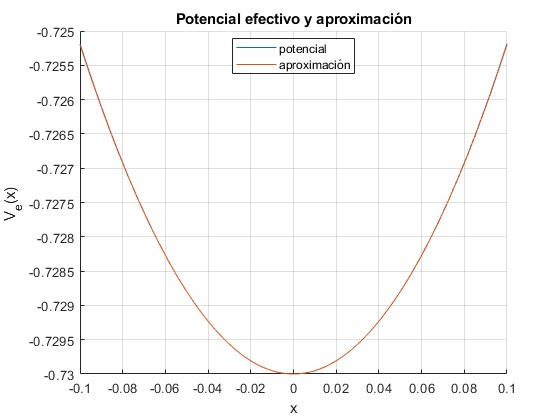
Apenas se distingue entre el potencial efectivo exacto y el aproximado en las proximidades de z_e=0. Las oscilaciones de las dos partículas unidas al muelle elástico son casi armónicas

La masa efectiva es, μ=2m

La frecuencia angular de las oscilaciones es

${\displaystyle {\omega }_{>}^2=\frac{4k{r}_0\left(\frac{1}{R}-\frac{1}{\xi }\right)}{2m}=2\frac{k{r}_0}{m}\left(\frac{1}{R}-\frac{1}{\xi }\right),\omega >{\omega }_c}$

Se puede expresar ω_> en términos de magnitudes adimensionales ω/ω_c y ε=r₀/R

${\displaystyle \frac{{\omega }_{>}^2}{{\omega }_0^2}=\left(1-\epsilon \right)\left(\frac{{\omega }^2}{{\omega }_c^2}-1\right),\omega >{\omega }_c}$

• Para ω<ω_c, la posición de equilibrio estable es $z_e=\sqrt{R^2-{\xi }^2}$ , la otra es simétrica

La derivada segunda del potencial efectivo en la posición de equilibrio vale

${\displaystyle k_e=\frac{4k{r}_0}{\xi }\left(\frac{R^2}{{\xi }^2}-1\right)}$

La energía potencial V_e(z) efectiva en las proximidades de z_e se puede aproximar y expresar en términos de magnitudes adimensionales ω/ω_c y ε=r₀/R

${\displaystyle \begin{array}{l}{V}_e(z)\approx V_e(z_e)+\frac{1}{2}\frac{4k{r}_0}{\xi }\left(\frac{R^2}{{\xi }^2}-1\right){\left(z-z_e\right)}^2\\ V_e(z)\approx 2k{\left(\xi -r_0\right)}^2-m{\omega }^2{\xi }^2+\frac{2k{r}_0}{\xi }\left(\frac{R^2}{{\xi }^2}-1\right){\left(z-\sqrt{R^2-{\xi }^2}\right)}^2\\ \frac{V_e(z)}{2k{R}^2}\approx {\left(\frac{\epsilon }{\left(1-\frac{{\omega }^2}{{\omega }_0^2}\right)}-\epsilon \right)}^2-\frac{{\omega }^2}{{\omega }_0^2}\frac{{\epsilon }^2}{{\left(1-\frac{{\omega }^2}{{\omega }_0^2}\right)}^2}+\left(1-\frac{{\omega }^2}{{\omega }_0^2}\right)\left(\frac{{\left(1-\frac{{\omega }^2}{{\omega }_0^2}\right)}^2}{{\epsilon }^2}-1\right){\left(\frac{z}{R}-\sqrt{1-\frac{{\epsilon }^2}{{\left(1-\frac{{\omega }^2}{{\omega }_0^2}\right)}^2}}\right)}^2\\ \zeta =1-\frac{{\omega }^2}{{\omega }_0^2}=1-\left(1-\epsilon \right)\frac{{\omega }^2}{{\omega }_c^2}\\ \frac{V_e(x)}{2k{R}^2}\approx {\epsilon }^2{\left(\frac{1}{\zeta }-1\right)}^2-\left(1-\zeta \right)\frac{{\epsilon }^2}{{\zeta }^2}+\zeta \left(\frac{{\zeta }^2}{{\epsilon }^2}-1\right){\left(x-\sqrt{1-\frac{{\epsilon }^2}{{\zeta }^2}}\right)}^2\end{array}}$

Representamos la energía potencial exacta y aproximada tomando el término constante y el primer término del desarrollo en serie, para ε=0.5 y para ω/ω_c=1.4

ex=0.5; %cociente r0/R
hold on
W=0.4; %w/W-c
f=@(x) (sqrt(1-x.^2)-ex).^2-(1-ex)*W^2*(1-x.^2); %exacto
xe=sqrt(1-ex^2/(1-(1-ex)*W^2)^2); %equilibrio
%aproximado
Z=1-(1-ex)*W^2;
g=@(x) ex^2*(1/Z-1)^2-(1-Z)*ex^2/Z^2+Z*(Z^2/ex^2-1)*(x-sqrt(1-ex^2/Z^2)).^2;
fplot(f,[xe-0.1,xe+0.1])
fplot(g,[xe-0.1,xe+0.1])
line([xe,xe],[0,f(xe)],'lineStyle','--')
hold off
grid on
xlabel('x')
legend('potencial','aproximación','location','best')
ylabel('V_e(x)')
title('Potencial efectivo y aproximación')



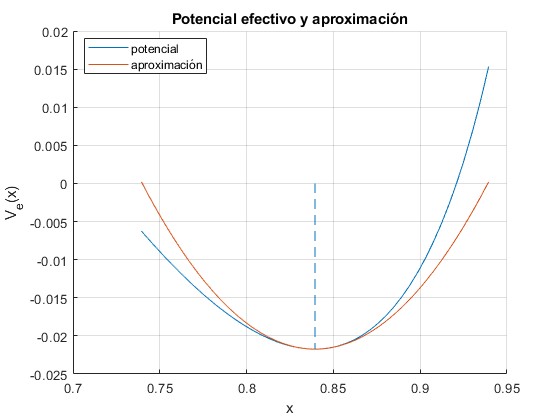
Se aprecian diferencias entre el potencial efectivo exacto y el aproximado en las proximidades de $z_e=\sqrt{R^2-{\xi }^2}$. Las oscilaciones de las dos partículas unidas al muelle elástico no son armónicas

La masa efectiva es $\mu =2m\frac{R^2}{{\xi }^2}$

La frecuencia angular de las oscilaciones es

${\displaystyle {\omega }_{<}^2=\frac{\frac{4k{r}_0}{\xi }\left(\frac{R^2}{{\xi }^2}-1\right)}{2m\frac{R^2}{{\xi }^2}}=2\frac{k}{m}\frac{r_0}{R}\frac{\xi }{R}\left(\frac{R^2}{{\xi }^2}-1\right),\omega <{\omega }_c}$

Se puede expresar ω_> en términos de magnitudes adimensionales ω/ω_c y ε=r₀/R

${\displaystyle \begin{array}{l}\frac{{\omega }_{<}^2}{{\omega }_0^2}={\epsilon }^2\frac{1}{1-\left(1-\epsilon \right)\frac{{\omega }^2}{{\omega }_c^2}}\left(\frac{1}{{\epsilon }^2}\left(1-\left(1-\epsilon \right)\frac{{\omega }^2}{{\omega }_c^2}\right)-1\right)\\ \frac{{\omega }_{<}^2}{{\omega }_0^2}=\left(1-\epsilon \right)\frac{\left(1+\epsilon +\left(1-\epsilon \right)\frac{{\omega }^4}{{\omega }_c^4}-2\frac{{\omega }^2}{{\omega }_c^2}\right)}{1-\left(1-\epsilon \right)\frac{{\omega }^2}{{\omega }_c^2}},\omega <{\omega }_c\end{array}}$

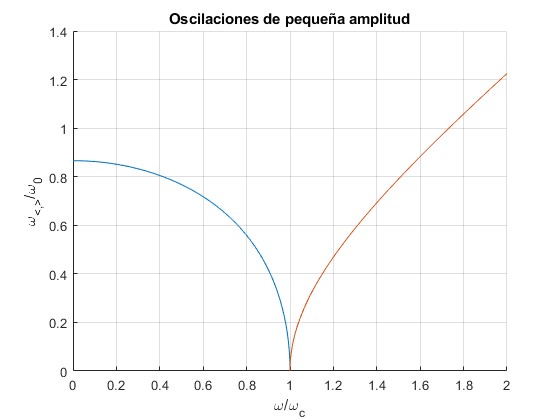
Representamos ω_</ω₀ y ω_>/ω₀ en función de ω/ω_c para ε=0.5. Cuando ω→ω_c, el equilibrio es indiferente, no hay oscilaciones, ω=0.

ex=0.5; %cociente r0/R
hold on
f=@(x) sqrt((1-ex)*(x.^2-1)); %w>w_c
g=@(x) sqrt((1-ex)*(1+ex+(1-ex)*x.^4-2*x.^2)./(1-(1-ex)*x.^2)); %w<w_c
fplot(g,[0,1])
fplot(f,[1,2])
hold off
grid on
xlabel('\omega/\omega_c')
ylabel('\omega_{<,>}/\omega_0')
title('Oscilaciones de pequeña amplitud')

Ecuación del movimiento

Hemos calculado la lagrangiana L=E_k-E_p que depende de z y dz/dt, la ecuación del movimiento es

${\displaystyle \begin{array}{l}L=m\frac{R^2}{R^2-z^2}{\left(\frac{dz}{dt}\right)}^2+m\left(R^2-z^2\right){\omega }^2-2k{\left(\sqrt{R^2-z^2}-r_0\right)}^2\\ \frac{d}{dt}\frac{\partial L}{\partial \dot{z}}-\frac{\partial L}{\partial z}=0\\ 2m\frac{R^2}{R^2-z^2}\frac{d^{2}z}{d{t}^2}+2m{R}^2\frac{dz}{dt}\frac{2z\frac{dz}{dt}}{{\left(R^2-z^2\right)}^2}-2m{R}^{2}z{\left(\frac{dz}{dt}\right)}^2\frac{1}{{\left(R^2-z^2\right)}^2}+2m{\omega }^{2}z-4k\left(\sqrt{R^2-z^2}-r_0\right)\frac{z}{\sqrt{R^2-z^2}}=0\\ \frac{d^{2}z}{d{t}^2}+\frac{z}{R^2-z^2}{\left(\frac{dz}{dt}\right)}^2+\frac{1}{R^2}\left({\omega }^2-2\frac{k}{m}\right)z\left(R^2-z^2\right)+2\frac{k}{m}\frac{r_0}{R^2}z\sqrt{R^2-z^2}=0\\ \frac{d^{2}z}{d{t}^2}+\frac{z}{R^2-z^2}{\left(\frac{dz}{dt}\right)}^2+\frac{1}{R^2}\left({\omega }^2-{\omega }_0^2\right)z\left(R^2-z^2\right)+{\omega }_0^2\frac{r_0}{R^2}z\sqrt{R^2-z^2}=0\end{array}}$

Para resolver numéricamente, es mejor expresar la ecuación diferencial en términos de variables adimensionales, x=z/R, τ=ω₀t/(2π), ω/ω_c y ε

${\displaystyle \begin{array}{l}\frac{{\omega }_0^2}{4{\pi }^2}\frac{d^{2}x}{d{\tau }^2}+\frac{x}{1-x^2}\frac{{\omega }_0^2}{4{\pi }^2}{\left(\frac{dx}{d\tau }\right)}^2+\left({\omega }^2-{\omega }_0^2\right)x\left(1-x^2\right)+{\omega }_0^2\epsilon x\sqrt{1-x^2}=0\\ \frac{d^{2}x}{d{\tau }^2}+\frac{x}{1-x^2}{\left(\frac{dZ}{d\tau }\right)}^2+\frac{4{\pi }^2}{{\omega }_0^2}\left({\omega }^2-{\omega }_0^2\right)x\left(1-x^2\right)+4{\pi }^2\epsilon x\sqrt{1-x^2}=0\\ \frac{d^{2}x}{d{\tau }^2}+\frac{x}{1-x^2}{\left(\frac{dx}{d\tau }\right)}^2+4{\pi }^2\frac{1-\epsilon }{{\omega }_c^2}\left({\omega }^2-\frac{{\omega }_c^2}{1-\epsilon }\right)x\left(1-x^2\right)+4{\pi }^2\epsilon x\sqrt{1-x^2}=0\\ \frac{d^{2}x}{d{\tau }^2}+\frac{x}{1-x^2}{\left(\frac{dx}{d\tau }\right)}^2+4{\pi }^2\left(\left(1-\epsilon \right)\frac{{\omega }^2}{{\omega }_c^2}-1\right)x\left(1-x^2\right)+4{\pi }^2\epsilon x\sqrt{1-x^2}=0\end{array}}$

donde -1≤x≤1

Para resolver la ecuación diferencial consideramos los dos casos ω>ω_c y ω<ω_c separadamente

• ω>ω_c

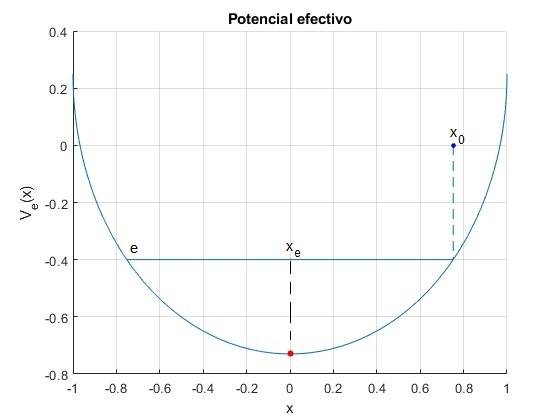
Sea ε=0.5 y ω/ω_c=1.4

Representamos el potencial efectivo V_e(x), tiene un mínimo (punto de color rojo) en x_e=z_e/R=0, cuyo valor es V_e(0)=-0.73. El valor en el extremo del intervalo x=1 es V_e(1)=0.25

Tomamos un valor de la energía, por ejemplo, e=-0.4 comprendido entre el mínimo y V_e(1). Los puntos de retorno, aquellos en los que la velocidad es cero, V_e(x)=e, se obtienen resolviendo la ecuación trascendente utilizando la función fzero de MATLAB

${\displaystyle {\left(\sqrt{1-x^2}-\epsilon \right)}^2-\left(1-\epsilon \right)\frac{{\omega }^2}{{\omega }_c^2}\left(1-x^2\right)=e}$

El resultado es, x₀=0.7524

ex=0.5; %cociente r0/R
hold on
W=1.4; %cociente w/w_c
f=@(x) (sqrt(1-x.^2)-ex).^2-(1-ex)*W^2*(1-x.^2); %x=z/R, 
fplot(f,[-1,1])
plot(0,f(0),'ro','markersize',4,'markerfacecolor','r') %mínimo
e=-0.4; %energía
g=@(x) f(x)-e;
x0=fzero(g,[0,1]); %retorno
line([-x0,x0],[e,e])
line([x0,x0],[0,e], 'lineStyle','--')
plot(x0,0,'bo','markersize',3,'markerfacecolor','b') %retorno
hold off
grid on
xlabel('x')
ylabel('V_e(x)')
title('Potencial efectivo')



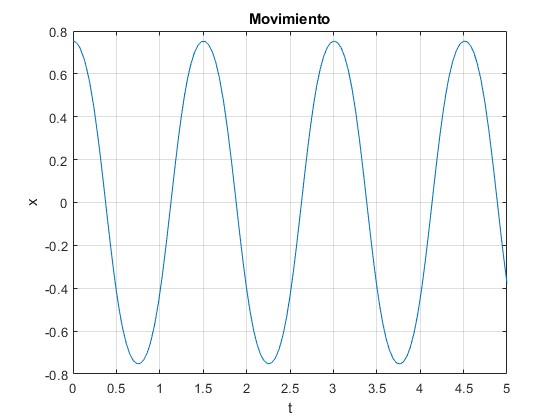
Supongamos que la partícula parte de la posición x₀ con velocidad nula. Resolvemos la ecuación del movimiento utilizando el procedimiento ode45 de MATLAB

ex=0.5;  %cociente r0/R
W=1.4;  %cociente w/w_c
e=-0.4; %energía
g=@(x) (sqrt(1-x^2)-ex)^2-(1-ex)*W^2*(1-x^2)-e;
x0=fzero(g,[0,1]); %retorno
f=@(t,x) [x(2); -x(1)*x(2)^2/(1-x(1)^2)-4*pi^2*((1-ex)*W^2-1)*x(1)*
(1-x(1)^2)-4*pi^2*ex*x(1)*sqrt(1-x(1)^2)]; 
[t,x]=ode45(f,[0,5],[x0,0]);
plot(t,x(:,1)) % tiempo, posición
grid on
xlabel('t')
ylabel('x')
title('Movimiento')

La energía potencial efectiva V_e(x) es simétrica por lo que la partícula oscila entre x₀ y -x₀ tal como vemos en la figura



Representamos las trayectorias en el espacio de las fases, en el eje horizontal x, en el eje vertical la velocidad dx/dτ, para diversos valores de la energía

Como la energía potencial efectiva es simétrica, basta resolver la ecuación difrencial desde x₀ a x=0

function pista_8 
     ex=0.5;  %cociente r0/R
     W=1.4;  %cociente w/w_c
     hold on
     %equilibrio x=0
     for e=-0.6:0.2:0.1
        g=@(x) (sqrt(1-x^2)-ex)^2-(1-ex)*W^2*(1-x^2)-e;
        x0=fzero(g,[0,1]); %retorno
        f=@(t,x) [x(2); -x(1)*x(2)^2/(1-x(1)^2)-4*pi^2*((1-ex)*W^2-1)*
x(1)*(1-x(1)^2)-4*pi^2*ex*x(1)*sqrt(1-x(1)^2)]; 
        opts=odeset('events',@stop_pista);
        [~,x]=ode45(f,[0,10],[x0,0], opts);
        xx=x(:,1);
        yy=x(:,2);
        plot([-fliplr(xx),xx],[yy,yy],'r') % posición, velocidad
        plot([-fliplr(xx),xx],[-yy,-yy],'r') 
     end
     hold off
     grid on
     xlabel('x')
     ylabel('dx/d\tau')
     title('Espacio de las fases')

     function [value,isterminal,direction]=stop_pista(~,x)
        value=x(1);
        isterminal=1;    
        direction=-1; 
     end
end



• ω<ω_c

Sea ε=0.5 y ω/ω_c=0.4

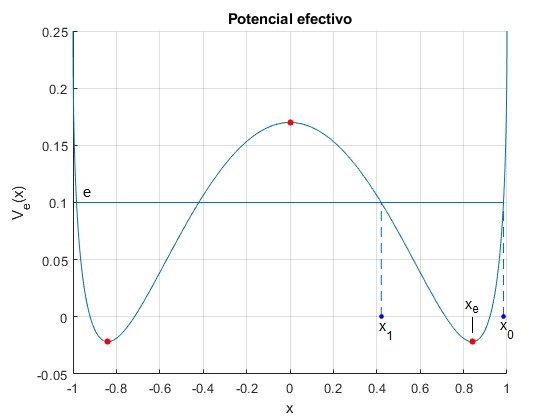
Representamos el potencial efectivo V_e(x), tiene un mínimo (punto de color rojo) en x_e=z_e/R=0.8394, cuyo valor es V_e(x_e)=-0.0217 y un máximo en x=0, cuyo valor es V_e(0)=0.1700. El valor en el extremo del intervalo x=1 es V_e(1)=0.25

Se presentan dos posibles casos:

• Energía, V_e(x_e)<e<V_e(0)

Tomamos un valor de la energía comprendido entre el mínimo y el máximo, por ejemplo, e=0.1. Los puntos de retorno, aquellos en los que la velocidad es cero, V_e(x)=e, se obtienen resolviendo la ecuación trascendente utilizando la función fzero de MATLAB como en el caso anterior

El punto de retorno comprendido entre x_e y x=1 es x₀=0.9837 y el comprendido entre x=0 y x_e es x₁=0.4206

ex=0.5; %cociente r0/R
hold on
W=0.4;%w/w_c
f=@(x) (sqrt(1-x.^2)-ex).^2-(1-ex)*W^2*(1-x.^2); %x=z/R
fplot(f,[-1,1])
xe=sqrt((1-ex)*(1+ex+(1-ex)*W^4-2*W^2))/(1-(1-ex)*W^2); %equilibrio
plot(xe,f(xe),'ro','markersize',4,'markerfacecolor','r') %mínimo
plot(-xe,f(xe),'ro','markersize',4,'markerfacecolor','r') %mínimo
plot(0,f(0),'ro','markersize',4,'markerfacecolor','r') %máximo
e=0.1; %energía
g=@(x) f(x)-e;
x0=fzero(g,[xe,1]);
x1=fzero(g,[0,xe]);
line([-x0,x0],[e,e])
line([x0,x0],[0,e], 'lineStyle','--')
line([x1,x1],[0,e], 'lineStyle','--')
plot(x0,0,'bo','markersize',3,'markerfacecolor','b') %retorno
plot(x1,0,'bo','markersize',3,'markerfacecolor','b') %retorno
hold off
grid on
xlabel('x')
ylabel('V_e(x)')
title('Potencial efectivo'



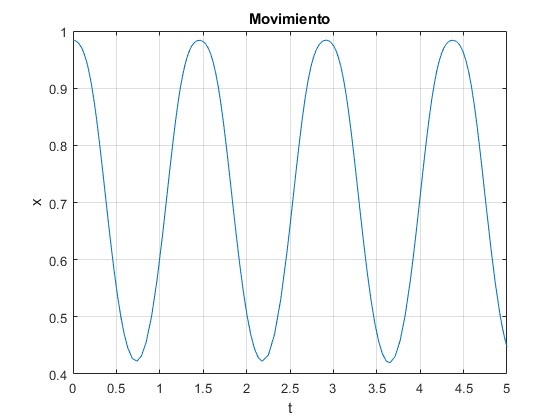
Supongamos que la partícula parte de la posición x₀ con velocidad nula. Resolvemos la ecuación del movimiento utilizando el procedimiento ode45 de MATLAB

ex=0.5;  %cociente r0/R
W=0.4;  %cociente w/w_c
e=0.1; %energía
g=@(x) (sqrt(1-x^2)-ex)^2-(1-ex)*W^2*(1-x^2)-e;
xe=sqrt((1-ex)*(1+ex+(1-ex)*W^4-2*W^2))/(1-(1-ex)*W^2); %equilibrio
x0=fzero(g,[xe,1]); %retorno
f=@(t,x) [x(2); -x(1)*x(2)^2/(1-x(1)^2)-4*pi^2*((1-ex)*W^2-1)*x(1)*
(1-x(1)^2)-4*pi^2*ex*x(1)*sqrt(1-x(1)^2)]; 
[t,x]=ode45(f,[0,5],[x0,0]);
plot(t,x(:,1)) % tiempo, posición
grid on
xlabel('t')
ylabel('x')
title('Movimiento')

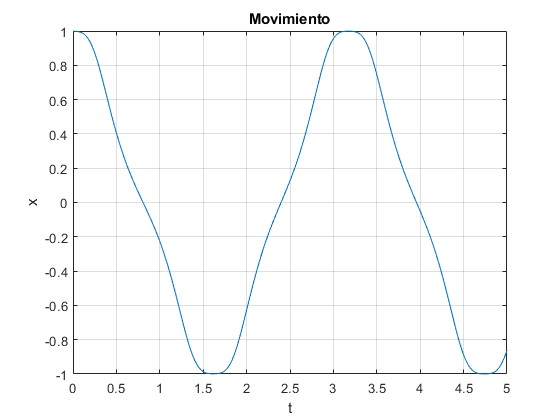
La partícula oscila entre x₀ y x₁



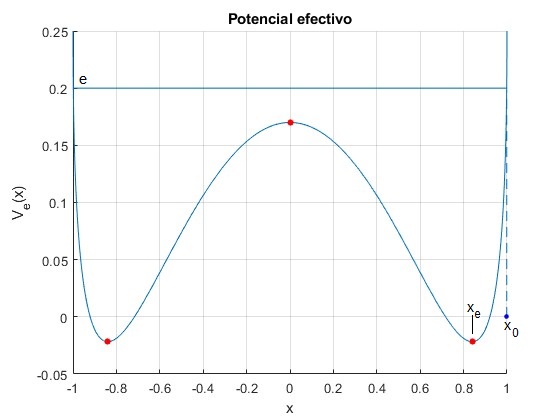
• Energía, V_e(0)<e<V_e(1)

Tomamos un valor de la energía comprendido entre el máximo V_e(0)=0.17 y V_e(1)=0.25, por ejemplo, e=0.2. Los puntos de retorno, aquellos en los que la velocidad es cero, V_e(x)=e, se obtienen resolviendo la ecuación trascendente utilizando la función fzero de MATLAB como en el caso anterior

El punto de retorno está comprendido entre x_e y x=1 es x₀=0.9986

ex=0.5; %cociente r0/R
hold on
W=0.4;%w/w_c
f=@(x) (sqrt(1-x.^2)-ex).^2-(1-ex)*W^2*(1-x.^2); %x=z/R
fplot(f,[-1,1])
xe=sqrt((1-ex)*(1+ex+(1-ex)*W^4-2*W^2))/(1-(1-ex)*W^2); %equilibrio
plot(xe,f(xe),'ro','markersize',4,'markerfacecolor','r') %mínimo
plot(-xe,f(xe),'ro','markersize',4,'markerfacecolor','r') %mínimo
plot(0,f(0),'ro','markersize',4,'markerfacecolor','r') %máximo
e=0.2; %energía
g=@(x) f(x)-e;
x0=fzero(g,[xe,1]); %retorno
line([-x0,x0],[e,e])
line([x0,x0],[0,e], 'lineStyle','--')
plot(x0,0,'bo','markersize',3,'markerfacecolor','b') %retorno
hold off
grid on
xlabel('x')
ylabel('V_e(x)')
title('Potencial efectivo')



Supongamos que la partícula parte de la posición x₀ con velocidad nula. Resolvemos la ecuación del movimiento utilizando el procedimiento ode45 de MATLAB

ex=0.5;  %cociente r0/R
W=0.4;  %cociente w/w_c
e=0.2; %energía
g=@(x) (sqrt(1-x^2)-ex)^2-(1-ex)*W^2*(1-x^2)-e;
xe=sqrt((1-ex)*(1+ex+(1-ex)*W^4-2*W^2))/(1-(1-ex)*W^2); %equilibrio
x0=fzero(g,[xe,1]); %retorno
f=@(t,x) [x(2); -x(1)*x(2)^2/(1-x(1)^2)-4*pi^2*((1-ex)*W^2-1)*
x(1)*(1-x(1)^2)
-4*pi^2*ex*x(1)*sqrt(1-x(1)^2)]; 
[t,x]=ode45(f,[0,5],[x0,0]);
plot(t,x(:,1)) % tiempo, posición
grid on
xlabel('t')
ylabel('x')
title('Movimiento')

La energía potencial efectiva V_e(x) es simétrica por lo que la partícula oscila entre x₀ y -x₀ tal como vemos en la figura



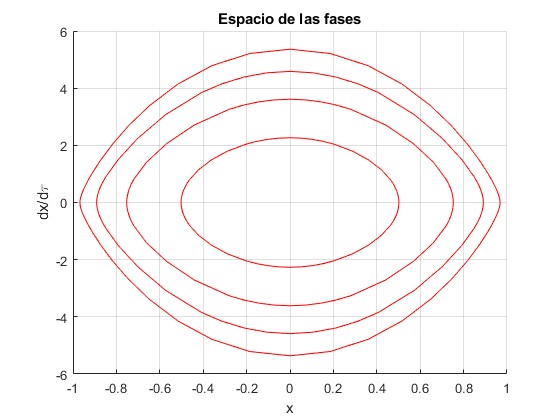
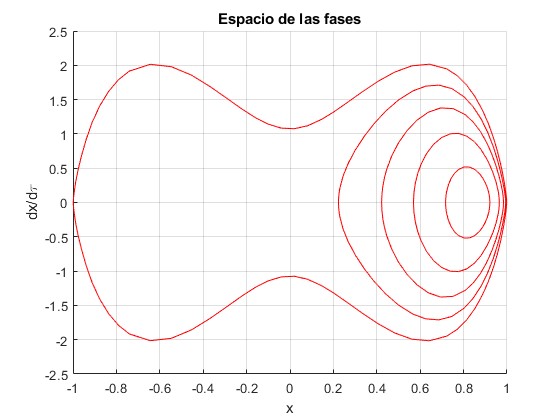
Representamos las trayectorias en el espacio de las fases, en el eje horizontal x, en el eje vertical la velocidad dx/dτ, para diversos valores de la energía

Como la energía potencial efectiva no es simétrica,resolvemos la ecuación diferencial desde x₀ a -x₀ donde la velocidad dx/dτ vuelve a ser cero

function pista_9 
    ex=0.5;  %cociente r0/R
    W=0.4;  %cociente w/w_c
    hold on
    for e=0:0.05:0.2
        g=@(x) (sqrt(1-x^2)-ex)^2-(1-ex)*W^2*(1-x^2)-e;
        ze=sqrt((1-ex)*(1+ex+(1-ex)*W^4-2*W^2))/(1-(1-ex)*W^2);
        x0=fzero(g,[ze,1]); %retorno
        f=@(t,x) [x(2); -x(1)*x(2)^2/(1-x(1)^2)-4*pi^2*((1-ex)*W^2-1)*x(1)
*(1-x(1)^2)-4*pi^2*ex*x(1)*sqrt(1-x(1)^2)]; 
        opts=odeset('events',@stop_pista);
        [~,x]=ode45(f,[0,10],[x0,0], opts);
        xx=x(:,1);
        yy=x(:,2);
        plot(xx,yy,'r') % posición, velocidad
        plot(xx,-yy,'r') 
    end
    hold off
    grid on
    xlabel('z/R')
    ylabel('v')
    title('Espacio de las fases')

    function [value,isterminal,direction]=stop_pista(~,x)
        value=x(2);
        isterminal=1;    
        direction=0; 
    end  
end

Referencias

Fredy Ochoa, Jorge Clavijo. Bead, hoop and spring as a classical spontaneous symmetry breaking problem. Eur. J. Phys. 27 (2006) pp. 1277–1288

O.L. de Lange, J. Pierrus. Solved Problems in Classical Mechanics. Analytical and numerical solutions with comments. Oxford University Press. Secciones 10.14, 10.15, 13.16