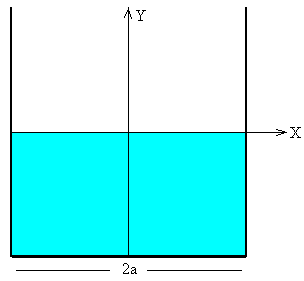
El líquido se coloca en una celda de material plástico transparente de forma paralepipédica de dimensiones 138×5×265 cm. En la experiencia simulada, estudiaremos una lámina de líquido contenida en un recipiente de forma rectangular que gira alrededor del eje de simetría paralelo al lado mayor. Consideramos despreciables los efectos debidos a tensión superficial.

En la figura de la izquierda, el recipiente de anchura 2a está en reposo ω=0, por lo que la superficie del líquido es horizontal. Establecemos un sistema de referencia NO inercial (vinculado al observador en rotación) de modo que el eje de rotación es el eje Y y la superficie del líquido en reposo es el eje X.

Cuando el eje del recipiente se conecta a un motor de velocidad angular variable, la superficie del líquido cambia de forma. Vamos a determinar la ecuación que describe la forma de la superficie a partir de las fuerzas que se ejercen sobre las moléculas de fluido.

Desde el punto de vista del observador en rotación, las fuerzas que actúan sobre una partícula de masa m situada en su superficie, a una distancia x del eje de rotación, son

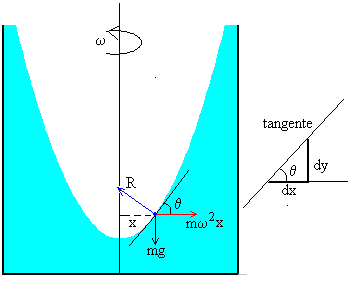
• El peso, $-mg\widehat{j}$
• La fuerza centrífuga, $m{\omega }^{2}x\widehat{i}$
• La fuerza $\overrightarrow{R}$ que ejercen las otras partículas de fluido sobre la partícula considerada

Desde el punto de vista del observador no inercial, la partícula está en equilibrio, de modo que la resultante de las fuerzas que actúan sobre la partícula debe ser cero

${\displaystyle \overrightarrow{R}-mg\widehat{j}+m{\omega }^{2}x\widehat{i}=0}$

La forma de la superficie del líquido en equilibrio será tal que $\overrightarrow{R}$ es perpendicular a la tangente a la curva en cada punto x. Como vemos en la figura

${\displaystyle \tan \theta =\frac{dy}{dx}=\frac{m{\omega }^{2}x}{mg}}$

Integrando tenemos

${\displaystyle y=\frac{1}{2}\frac{{\omega }^2}{g}{x}^2+c}$

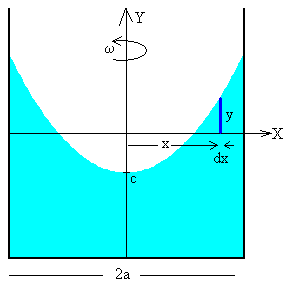
que es la ecuación de una parábola simétrica respecto del eje Y.

Para determinar la constante de integración c o el punto más bajo de la parábola, supondremos que el líquido es incompresible. Comparando la situación inicial cuando la superficie del fluido es horizontal con la situación final, cuando la velocidad angular de rotación es ω.

En la situación inicial, la forma de la superficie es el segmento de la recta y=0 comprendido entre -a y a.

Observaremos, que el líquido se hunde por la parte cercana al eje de rotación y se eleva en la parte colindante con las paredes del recipiente. El área total debe ser cero como al principio, cuando la lámina está en reposo.

${\displaystyle {\displaystyle \underset{0}{\overset{a}{\int }}y·dx=0}}$

La ordenada c del punto más bajo de la parábola valdrá, entonces

${\displaystyle c=-\frac{1}{6}\frac{{\omega }^2{a}^2}{g}}$

La ecuación de la parábola será, finalmente

${\displaystyle y=\frac{{\omega }^2}{2g}\left(x^2-\frac{a^2}{3}\right)}$

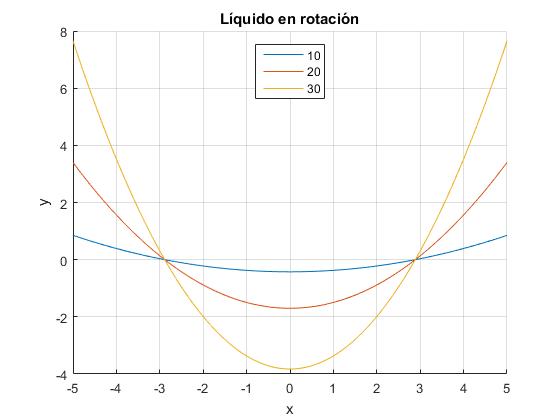
Cualquiera que sea la velocidad angular de rotación ω, las parábolas pasan por el punto $\left(\frac{a}{\sqrt{3}},0\right)$ Una molécula situada en este punto, no cambia de posición.

x=linspace(-5,5,100);
a=5;
hold on
for w=[10,20,30]
    y=w^2*(x.^2-a^2/3)/(2*9.8*100);
    plot(x,y,'displayName',num2str(w))
end
legend('-DynamicLegend','location','north')
grid on
xlabel('x')
ylabel('y')
title('Líquido en rotación')

Actividades

Se introduce

• La velocidad angular de rotación ω, en el control titulado Velocidad angular
• La anchura de la lámina de fluido se ha fijado en el valor 2a=10 cm.

Se pulsa el botón titulado Nuevo

Observamos, en la parte inferior izquierda, la lámina de fluido en rotación sobre una plataforma giratoria.

Observamos las fuerzas que actúan sobre una partícula de fluido situada en su superficie a una distancia x del eje de rotación. La abscisa x se establece en el control titulado Fuerzas en x:.

• El peso de la partícula (flecha de color negro)
• la fuerza centrífuga (en color rojo) aumenta con la distancia x al eje de rotación.
• La resultante (en color azul) es siempre perpendicular a la superficie.

Energías

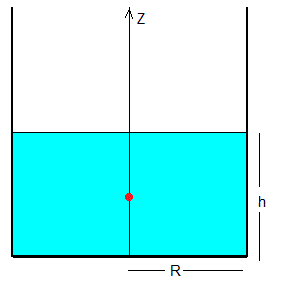
Consideremos un cubo de radio R, que está lleno de líquido hasta una altura h. Si el líquido con el cubo gira con velocidad angular constante ω alrededor de su eje, la superficie del líquido será la de un paraboloide de revolución cuyo eje es el eje del cilindro.

La ecuación de la parábola simétrica respecto del eje Z es

${\displaystyle z=\frac{1}{2}\frac{{\omega }^2}{g}{r}^2+z_0}$

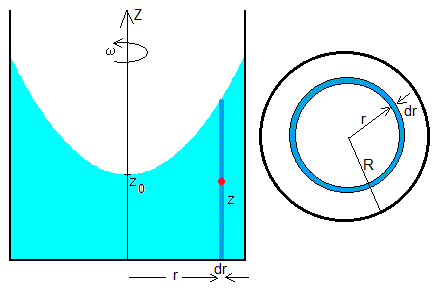
Para determinar la constante de integración z₀ o el punto más bajo de la parábola, supondremos que el líquido es incompresible. Comparamos la situación inicial cuando la superficie del fluido es horizontal con la situación final, cuando la velocidad angular de rotación es ω.

En la situación inicial, el volumen de fluido contenido en un cilindro de radio R y altura h es πR²h

Cuando el cubo gira con velocidad angular ω, la misma masa de agua se obtiene sumando las masas de agua contenidas en las capas cilíndricas de radio r, espesor dr y altura z.

${\displaystyle \begin{array}{l}V={\displaystyle \underset{0}{\overset{R}{\int }}2\pi r·z·dr}=2\pi {\displaystyle \underset{0}{\overset{R}{\int }}\left(\frac{1}{2}\frac{{\omega }^2}{g}{r}^2+z_0\right)}r·dr\\ \pi R^{2}h=2\pi \left(\frac{1}{8}\frac{{\omega }^2}{g}{R}^4+\frac{1}{2}{z}_0{R}^2\right)\\ z_0=h-\frac{{\omega }^2}{4g}{R}^2\end{array}}$

La ecuación de la parábola es

${\displaystyle z=\frac{{\omega }^2}{2g}{r}^2+h-\frac{{\omega }^2{R}^2}{4g}}$

z₀ se hace cero para una velocidad angular máxima, ω_m

${\displaystyle \frac{{\omega }_m^2}{4g}{R}^2=h}$

Para esta velocidad la altura z de la capa de fluido más externa, en contacto con las paredes del recipiente, r=R, vale z=2h. El agua empieza a derramarse por el borde del cubo medio lleno de agua.

Energía potencial

El centro de masas se encuentra a una altura h/2. La energía potencial inicial es mgh/2, la masa de agua es m=ρ(πR²h)

En la situación final, el centro de masa de una capa cilíndrica concéntrica de radio r, espesor, dr y altura z, se encuentra a z/2 de altura.

${\displaystyle \begin{array}{l}{E}_p={\displaystyle \underset{0}{\overset{R}{\int }}\rho \left(2\pi r·dr·z\right)}g\frac{z}{2}=\pi \rho g{{\displaystyle \underset{0}{\overset{R}{\int }}r\left(\frac{1}{2}\frac{{\omega }^2}{g}{r}^2+z_0\right)}}^{2}dr=\\ \pi \rho g\left(\frac{R^6}{24}\frac{{\omega }^4}{g^2}+\frac{R^2}{2}{z}_0^2+\frac{R^4}{4}{z}_0\frac{{\omega }^2}{g}\right)=\rho \pi R^{2}hg\left(\frac{h}{2}+\frac{{\omega }^4{R}^4}{96g^{2}h}\right)=mg\left(\frac{h}{2}+\frac{{\omega }^4{R}^4}{96g^{2}h}\right)\end{array}}$

Cuando el cubo está en rotación, el centro de masas del agua asciende y la energía potencial se incrementa

${\displaystyle \Delta E_p=m\frac{{\omega }^4{R}^4}{96gh}}$

Energía cinética

La energía cinética de rotación es

${\displaystyle E_k=\frac{1}{2}I{\omega }^2}$

Calculamos el momento de inercia de la masa contenida en la capa cilíndrica de radio r, espesor dr y altura z.

${\displaystyle \begin{array}{l}I={\displaystyle \underset{0}{\overset{R}{\int }}{r}^2\rho \left(2\pi r·dr·z\right)}=2\pi \rho {\displaystyle \underset{0}{\overset{R}{\int }}\left(\frac{1}{2}\frac{{\omega }^2}{g}{r}^5+z_0{r}^3\right)}dr=\\ 2\pi \rho \left(\frac{1}{12}\frac{{\omega }^2}{g}{R}^6+\frac{1}{4}{z}_0{R}^4\right)=\frac{\rho \pi R^4}{2}\left(\frac{{\omega }^2{R}^2}{12g}+h\right)=\frac{m{R}^2}{2}\left(\frac{{\omega }^2{R}^2}{12gh}+1\right)\end{array}}$

La expresión de la energía cinética de rotación es

${\displaystyle E_k=\frac{m{R}^2}{4}{\omega }^2\left(\frac{{\omega }^2{R}^2}{12gh}+1\right)}$

La suma de la energía cinética y la variación de energía potencial es

${\displaystyle \Delta E_p+E_k=m\frac{{\omega }^4{R}^4}{96gh}+\frac{m{R}^2}{4}{\omega }^2\left(\frac{{\omega }^2{R}^2}{12gh}+1\right)=\frac{m{R}^2}{4}{\omega }^2\left(1+\frac{{\omega }^2{R}^2}{8gh}\right)}$

Trabajo del momento aplicado al cubo que contiene agua

Para que la velocidad del cubo que contiene el agua se incremente de 0 a ω, hay que aplicar un momento que lo haga girar. El trabajo realizado en el movimiento de rotación es

${\displaystyle W={\displaystyle \underset{0}{\overset{\theta }{\int }}M·d\theta }}$

La ecuación de la dinámica de rotación, cuando el momento de inercia I no es constante

${\displaystyle M=\frac{d(I\omega )}{dt}=I\frac{d\omega }{dt}+\omega \frac{dI}{dt}}$

El trabajo realizado es

${\displaystyle \begin{array}{l}W={\displaystyle \underset{0}{\overset{\theta }{\int }}M·d\theta =}{\displaystyle \underset{0}{\overset{\theta }{\int }}\frac{d(I\omega )}{dt}·d\theta =}{\displaystyle \underset{0}{\overset{\omega }{\int }}\omega \left(\omega dI+Id\omega \right)}\\ W={\displaystyle \underset{0}{\overset{\omega }{\int }}\left(\frac{m{\omega }^3{R}^4}{12gh}+\frac{m{R}^2}{2}\omega \left(\frac{{\omega }^2{R}^2}{12gh}+1\right)\right)}d\omega ={\displaystyle \underset{0}{\overset{\omega }{\int }}\left(\frac{m{R}^4}{8gh}{\omega }^3+\frac{m{R}^2}{2}\omega \right)}d\omega \\ W=\frac{m{R}^2}{4}{\omega }^2\left(1+\frac{{\omega }^2{R}^2}{8gh}\right)\end{array}}$

Que coincide con la variación de energía

Oscilaciones de un cubo medio lleno de agua

Consideremos un cubo cilíndrico de radio R y altura 2h, medio lleno de agua (véase la figura del apartado anterior). El cubo se encuentra suspendido de un cable que cuelga del techo. Se gira el cubo un cierto ángulo θ₀ y se suelta, el cubo empieza a oscilar.

Vamos a calcular el periodo de la oscilación, suponiendo que el agua es un líquido con la suficiente viscosidad para que gire solidariamente con el cubo con la misma velocidad angular y por otra parte, la superficie del agua adopte el perfil parabólico que corresponde al equilibrio del líquido estudiado en el apartado anterior. Estas dos condiciones no son fáciles de cumplir si la velocidad angular de rotación es elevada, pues distintas capas cilíndricas concéntricas de agua tendrían diferentes velocidades angulares.

Supongamos que el cubo está colgado de un cable de constante K de torsión y se gira un ángulo θ₀. La energía inicial del sistema es la suma de la energía elástica de torsión del cable y la energía potencial gravitatoria del agua (el centro de masa del agua está a una altura h/2).

${\displaystyle \frac{1}{2}K{\theta }_0^2+\frac{1}{2}mgh}$

Cuando se suelta el cubo, el desplazamiento angular θ disminuye y aumenta la velocidad angular de rotación ω. Como consecuencia, cambia la distribución de masa, la energía potencial E_g se modifica y el momento de inercia respecto del eje Z de rotación se incrementa al alejarse el agua del eje. La energía del sistema será

${\displaystyle \frac{1}{2}I{\omega }^2+\frac{1}{2}K{\theta }^2+E_g}$

El momento de inercia inicial de un cilindro de radio R y altura h es

${\displaystyle I_0=\frac{1}{2}m{R}^2=\frac{1}{2}\rho h\pi R^4}$

Interpretamos ω_m, la velocidad angular máxima como el cociente

${\displaystyle {\omega }_m^2=\frac{4gh}{R^2}=\frac{2mgh}{I_0}}$

Calculamos el momento de inercia de la masa contenida en la capa cilíndrica de radio r, espesor dr y altura z, y sumamos para todas las capas

${\displaystyle \begin{array}{l}I={\displaystyle \underset{0}{\overset{R}{\int }}{r}^2\rho \left(2\pi r·dr·z\right)}=2\pi \rho {\displaystyle \underset{0}{\overset{R}{\int }}\left(\frac{1}{2}\frac{{\omega }^2}{g}{r}^5+z_0{r}^3\right)}dr=\\ 2\pi \rho \left(\frac{1}{12}\frac{{\omega }^2}{g}{R}^6+\frac{1}{4}{z}_0{R}^4\right)=\frac{\rho \pi R^4}{2}\left(\frac{{\omega }^2{R}^2}{12g}+h\right)=I_0+\rho \pi \frac{{\omega }^2{R}^6}{24g}=I_0\left(1+\frac{{\omega }^2}{3{\omega }_m^2}\right)\end{array}}$

El centro de masa de una capa cilíndrica concéntrica de radio r, espesor dr y altura z, se encuentra a z/2 de altura.

${\displaystyle \begin{array}{l}{E}_p={\displaystyle \underset{0}{\overset{R}{\int }}\rho \left(2\pi r·dr·z\right)}g\frac{z}{2}=\pi \rho g{{\displaystyle \underset{0}{\overset{R}{\int }}r\left(\frac{1}{2}\frac{{\omega }^2}{g}{r}^2+z_0\right)}}^{2}dr=\\ \pi \rho g\left(\frac{R^6}{24}\frac{{\omega }^4}{g^2}+\frac{R^2}{2}{z}_0^2+\frac{R^4}{4}{z}_0\frac{{\omega }^2}{g}\right)=\rho \pi R^{2}hg\left(\frac{h}{2}+\frac{{\omega }^4{R}^4}{96g^{2}h}\right)=\frac{1}{2}mgh\left(1+\frac{{\omega }^4}{3{\omega }_m^4}\right)\end{array}}$

El principio de conservación de la energía se escribe

${\displaystyle \frac{1}{2}K{\theta }_0^2+\frac{1}{2}mgh=\frac{1}{2}{I}_0\left(1+\frac{{\omega }^2}{3{\omega }_m^2}\right){\omega }^2+\frac{1}{2}K{\theta }^2+\frac{1}{2}mgh\left(1+\frac{{\omega }^4}{3{\omega }_m^4}\right)}$

Teniendo en cuenta, $I_0{\omega }_m^2=2mgh$, despejamos la velocidad angular de rotación ω

${\displaystyle \begin{array}{l}\frac{1}{3}\left(I_0{\omega }_m^2+mgh\right){\left(\frac{\omega }{{\omega }_m}\right)}^4+I_0{\omega }_m^2{\left(\frac{\omega }{{\omega }_m}\right)}^2-K\left({\theta }_0^2-{\theta }^2\right)=0\\ {\left(\frac{\omega }{{\omega }_m}\right)}^4+2{\left(\frac{\omega }{{\omega }_m}\right)}^2-\frac{K{\theta }_0^2}{mgh}\left(1-{\left(\frac{\theta }{{\theta }_0}\right)}^2\right)=0\\ {\left(\frac{\omega }{{\omega }_m}\right)}^2=\sqrt{\beta \left(1-{\left(\frac{\theta }{{\theta }_0}\right)}^2\right)+1}-1\end{array}}$

La velocidad angular de rotación ω=dθ/dt

${\displaystyle \begin{array}{l}\frac{d\theta }{dt}={\omega }_m\sqrt{\left\{\sqrt{\beta \left(1-{\left(\frac{\theta }{{\theta }_0}\right)}^2\right)+1}-1\right\}}\\ {\omega }_m{\displaystyle \underset{0}{\overset{P/4}{\int }}dt}={\displaystyle \underset{0}{\overset{{\theta }_0}{\int }}\frac{d\theta }{\sqrt{\left\{\sqrt{\beta \left(1-{\left(\frac{\theta }{{\theta }_0}\right)}^2\right)+1}-1\right\}}}}\\ P=4\frac{f\left({\theta }_0\right)}{{\omega }_m}\end{array}}$

El periodo P depende de la amplitud θ₀ de una forma similar a un péndulo simple, pero por razones completamente distintas. En el péndulo simple por que se deja de cumplir la aproximación sinθ≈θ, y en el cubo por que el momento de inercia y la energía potencial gravitatoria se modifican al cambiar la distribución de masa con la velocidad angular ω de rotación.

La función integrando tiende a ∞ en el límite superior, cuando θ→θ₀, lo que complica la aplicación de procedimientos numéricos para calcular la integral definida

Los periodos de oscilación del líquido contenido en el cubo son proporcionales a f(θ₀). Utilizamos el procedimiento integral de MATLAB para calcular la integral definida f(θ₀), para el valor del parámetro β=2 y para amplitudes de la oscilación θ₀ comprendidas entre 1° y 90°

beta=2;
theta_0=pi/180:pi/180:pi/2; %amplitudes
P=zeros(1,length(theta_0));
i=1;
for  x0=theta_0
    f=@(x) 1./sqrt(sqrt(beta*(1-x.^2/x0^2)+1)-1);
    P(i)=integral(f,0,x0);
    i=i+1;
end
plot(theta_0,P)
grid on
xlabel('\theta_0')
ylabel('f(\theta_0)')
title('Periodo de oscilación del cubo')

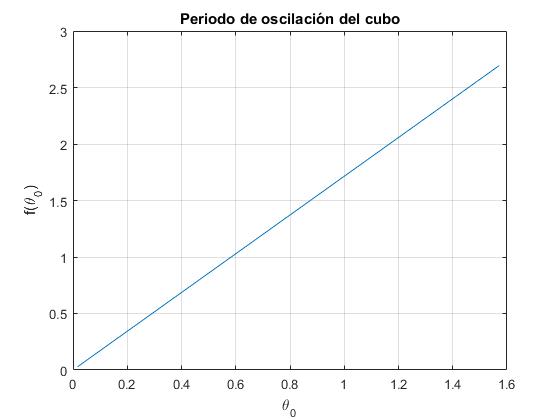
Observamos un comportamiento 'lineal' del periodo P respecto de la amplitud θ₀

Referencias

Carl E. Mungan. Trevor C. Lipscombe Newton's Rotating Water Bucket: A Simple Model Washington Academy of Sciences. Summmer 2013

Este artículo está disponible en la dirección: https://www.usna.edu/Users/physics/mungan/_files/documents/Publications/EJP17.pdf

Ranko Martin Artuković, Mirko Marušić. Water Leakage from a Rotating Cylindrical Tank. The Physics Teacher, Vol. 59, May 2021, pp. 360-362