El péndulo cónico

Supongamos una partícula de masa m que está conectada mediante una varilla de longitud l y de masa despreciable al eje vertical de un motor. La varilla se desvía del eje vertical un ángulo θ cuando la velocidad angular del motor es mayor que un cierto valor mínimo ω_c. La partícula describe entonces una circunferencia horizontal de radio l·sinθ. A este sistema se le denomina péndulo cónico.

Sistema de referencia inercial

Consideremos primero la situación más simple. Sustituyamos la varilla por un hilo inextensible y sin peso.

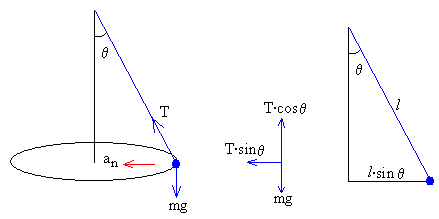
Como podemos apreciar en la figura, si la partícula de masa m describe una circunferencia de radio l·sinθ, las fuerzas que actúan sobre la partícula son:

El peso mg
La tensión del hilo T.

Sustituimos la tensión T por la acción simultánea de sus componentes rectangulares.

La partícula está en equilibrio a lo largo de eje vertical.

T·cosθ =mg

La partícula describe un movimiento circular uniforme en el plano horizontal, su aceleración es $a_{n} = ω^{2} l \sin θ$ y tiene la dirección radial y sentido hacia el centro de la circunferencia que describe. Aplicando la segunda ley de Newton

T·sinθ =mω ²·l·sinθ

Despejando T en la primera ecuación y sustituyéndola en la segunda, tenemos dos posibles soluciones

sinθ =0
ω ²·l·cosθ =g

Despejando cosθ en la segunda

$\cos θ = \frac{g}{l ω^{2}}$

Como cosθ ≤1, esta la solución existe solamente para ω²≥g/l. Es decir, el péndulo abandona su posición vertical solamente si se cumple dicha desigualdad.

Sistema de referencia no inercial

Para hacer funcionar al péndulo cónico deberemos sustituir el hilo por una varilla rígida de la misma longitud l que supondremos de masa despreciable. El extremo superior de la varilla estará fijado a un gozne en el eje de un motor que gira con velocidad angular ω . En el sistema de referencia que gira con la varilla, tenemos un sólido rígido (la varilla) con un punto fijo O y un sólo grado de libertad, el ángulo θ .

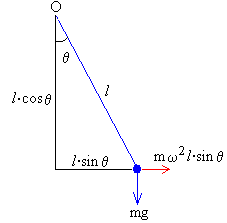
Debido a la fuerza centrífuga sobre la partícula, la varilla se desviará de su posición vertical un ángulo θ cuando la velocidad angular ω del motor sea lo suficientemente grande.

En el sistema de referencia en rotación con el eje del motor, la varilla se encontrará en equilibrio si el momento total del peso y de la fuerza centrífuga respecto del eje O es cero.

El momento del peso es

mg·l·sinθ .

El momento de la fuerza centrífuga es

mω²·l·sinθ ·l·cosθ

Ambos momentos tienen la misma dirección (perpendicular al plano formado por la fuerza y el punto O) pero sentidos opuestos. Igualando el momento total a cero

ml·sinθ (ω²l·cosθ -g)=0

Tenemos de nuevo, dos soluciones

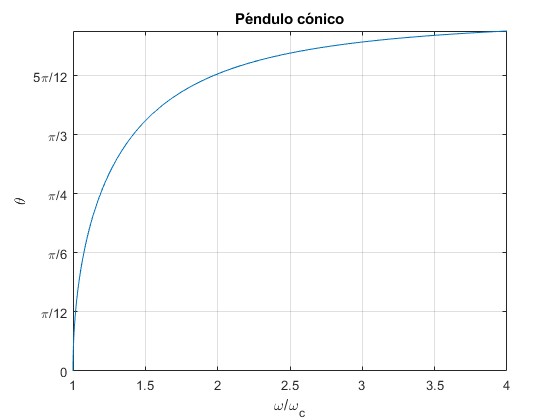
${\begin{cases} \sin θ = 0 \\ \cos θ = \frac{g}{ω^{2} l} \end{cases}$

Representamos el ángulo θ que hace el péndulo con la vertical en función del cociente ω/ω_c, donde ω_c²=g/l

fplot(@(x) acos(1./x.^2),[1,4])
set(gca,'YTick',0:pi/12:pi/2)
set(gca,'YTickLabel',{'0','\pi/12','\pi/6','\pi/4','\pi/3','5\pi/12','\pi/2'})
grid on
xlabel('\omega/\omega_c')
ylabel('\theta')
title('Péndulo cónico')

Equilibrio y estabilidad

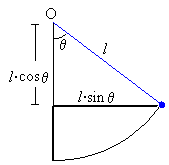
El peso es una fuerza conservativa. La energía potencial aumenta cuando la partícula se desvía un ángulo θ

E_g= mg(l-l·cosθ )

La fuerza centrífuga depende solamente de la distancia x al eje de rotación, es una fuerza conservativa similar a la que ejerce de un muelle elástico.

La fuerza que ejerce un muelle elástico es de sentido contrario al desplazamiento F=-kx, su energía potencial es positiva E_p=kx²/2

La fuerza centrífuga tiene el mismo sentido que el desplazamiento F=mω ²·x

$\int_{0}^{x} m ω^{2} x \cdot d x = 0 - E_{p}$

y su energía potencial será por tanto negativa $E_{c} = - \frac{1}{2} m ω^{2} x^{2}$ . La energía potencial inicial para x=0, se toma como E_c=0.

Cuando el péndulo se ha desviado un ángulo θ , el desplazamiento horizontal es x= l·sinθ . La energía potencial total de la partícula será la suma de ambas contribuciones E_p=E_g+E_c.

$E_{p} (θ) = m g l (1 - \cos θ) - \frac{1}{2} m ω^{2} l^{2} \sin^{2} θ$

Definimos el parámetro α=ω²l/g y representamos

$\frac{E_{p} (θ)}{m g l} = 1 - \cos θ - \frac{1}{2} α \sin^{2} θ$

hold on
for alfa=[0.5,2]
    f=@(x) 1-cos(x)-alfa*sin(x).^2/2;
    fplot(f,[-pi/6,pi])
end
th_e=acos(1/alfa); %mínimo para alfa=2
line([th_e,th_e],[-0.5,f(th_e)],'lineStyle','--','color','r')
hold off
grid on
set(gca,'XTick',-pi/6:pi/6:pi)
set(gca,'XTickLabel',{'-\pi/6', '0','\pi/6','\pi/3','\pi/2','2\pi/3','5\pi/6',
'\pi'})
xlim([-pi/6,pi])
legend('0.5','2','location','southeast')
xlabel('\theta')
ylabel('E_p(\theta)/(mgl)')
title('Energía potencial')

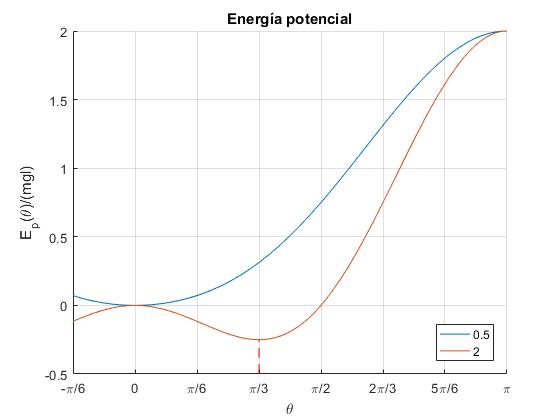
Observamos que para α>1, la energía potencial presenta un mínimo en θ=acos(1/α)

La condición de equilibrio se establece cuando E_p sea un extremo (máximo o mínimo)

$\frac{d E_{p}}{d θ} = m g l \cdot \sin θ - m l^{2} ω^{2} \sin θ \cdot \cos θ = 0$

Que proporciona dos soluciones

$\begin{array}{l} θ = 0, π \\ θ = \arccos \frac{g}{l ω^{2}} \end{array}$

Estabilidad

La estabilidad de la solución depende de la derivada segunda.

$\frac{d^{2} E_{p}}{d θ^{2}} = m g l \cdot cos θ - m l^{2} ω^{2} (\cos^{2} θ - \sin^{2} θ)$

Para la primera solución θ =0

$\frac{d^{2} E_{p}}{d θ^{2}} = m g l - m l^{2} ω^{2}$

Siempre que ω²<g/l, la derivada segunda es positiva y el equilibrio es estable, véase la figura de la izquierda
Si ω²>g/l, la derivada segunda es negativa y el equilibrio es inestable, véase la figura de la derecha

Para θ =π la derivada segunda es siempre negativa y el equilibrio es inestable, en ambas figuras
Para θ =arccos(g/lω²)

$\frac{d^{2} E_{p}}{d θ^{2}} = - \frac{m g^{2}}{ω^{2}} + m l^{2} ω^{2}$

Si ω²>g/l, la solución es estable, figura de la derecha

El péndulo cónico está por tanto, caracterizado por una velocidad angular crítica

$ω_{c} = \sqrt{\frac{g}{l}}$

por encima de la cual el péndulo se desvía de la vertical. Por debajo de esta velocidad angular crítica, el péndulo permanece en la posición vertical θ =0.

Actividades

Vamos a estudiar el comportamiento de un péndulo cónico que tiene una longitud l=1 m fijada en el programa interactivo.

Podemos cambiar la velocidad angular ω de rotación del motor, en el control titulado Velocidad angular.

Se pulsa el botón titulado Nuevo.

Si la velocidad angular de rotación ω es menor que el valor crítico $ω_{c} = \sqrt{9.8} rad/s$ el péndulo permanece en la posición vertical θ =0.
Si la velocidad angular de rotación ω es mayor que el valor crítico, el péndulo se desvía de la posición vertical un ángulo

$\cos θ = \frac{9.8}{ω^{2}}$

A la derecha, se representa la energía potencia E_p en función del ángulo θ en unidades mgl. Podemos observar que los mínimos y los máximos de la energía potencial, es decir, las posiciones de equilibrio estable e inestable.

Velocidad angular

Movimiento de rotación de una varilla delgada

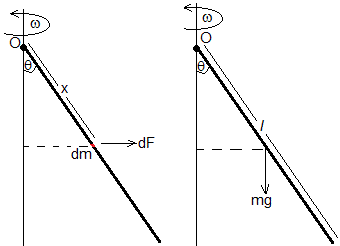
Cambiamos la varilla rígida de longitud l y de masa despreciable, unida a una masa puntual m por una varilla delgada de masa m y longitud l.

Cuando la varilla se desplaza un ángulo θ con la vertical y gira con velocidad angular ω, la fuerza centrífuga sobre un elemento diferencial de varilla de masa dm es

$d m \cdot ω^{2} x \sin θ = λ d x \cdot ω^{2} x \sin θ$

siendo λ=m/l la densidad lineal

El momento de esta fuerza respecto del eje de rotación en O, es

$\begin{array}{l} d M_{1} = (d m \cdot ω^{2} x \sin θ) x \cos θ = λ ω^{2} x^{2} \sin θ \cos θ \cdot d x \\ M_{1} = λ ω^{2} \sin θ \cos θ \int_{0}^{l} x^{2} d x = λ ω^{2} \sin θ \cos θ \cdot \frac{l^{3}}{3} = \frac{1}{3} m ω^{2} l^{2} \sin θ \cos θ \end{array}$

El peso mg actúa en el centro de la varilla y su momento respecto de O es

$M_{2} = - m g \frac{l}{2} \sin θ$

En el equilibrio, el momento total M₁+M₂=0, es nulo

$\begin{array}{l} \frac{1}{3} m ω^{2} l^{2} \sin θ \cos θ - m g \frac{l}{2} \sin θ = 0 \\ \sin θ (\frac{1}{3} ω^{2} l \cos θ - \frac{1}{2} g) = 0 \end{array}$

Las soluciones de esta ecuación son

${\begin{cases} \sin θ = 0 \\ \cos θ = \frac{3}{2} \frac{g}{ω^{2} l} \end{cases}$

Referencias

Dupré A., Janssen P.. An accurate determination of the acceleration of gravity g in the undergarduate laboratory. Am. J. Phys. 68 (8) August 2000, pp. 704-711.