Consideremos una varilla que puede girar en el plano horizontal con velocidad angular Ω constante alrededor de un eje perpendicular a la varilla. El anillo de masa m, que puede desplazarse a lo largo de la varilla sin rozamiento, se sujeta al eje mediante un muelle de constante k.

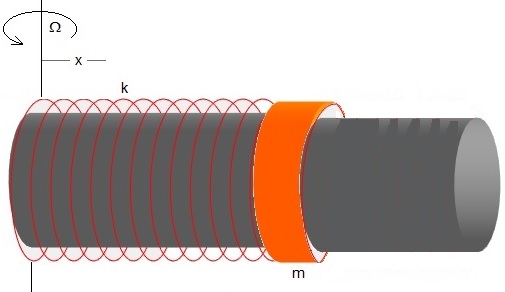
Representamos las fuerzas sobre el anillo de masa m en el instante t, cuando se ha desplazado x del eje de rotación y lleva una velocidad dx/dt

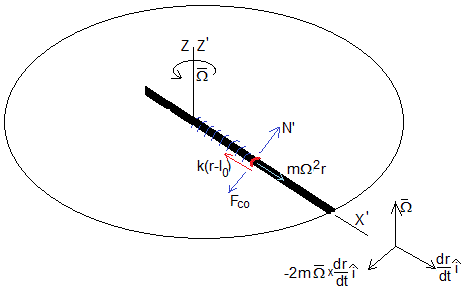
• La fuerza que ejerce el muelle elásticos, k(r-l₀). Siendo l₀ la longitud del muelle sin deformar

• La fuerza centrífuga, $-m\Omega \widehat{k}\times \left(\Omega \widehat{k}\times r\widehat{i}\right)$, de módulo mΩ²r, ambas en la dirección radial

• La fuerza de Coriolis, $\overrightarrow{F_{co}}=-2m\left(\Omega \widehat{k}\times \frac{dx}{dt}\widehat{i}\right)$ es perpendicular a la varilla y su sentido se indica en la figura. La reacción N' o fuerza que ejerce la varilla sobre el anillo es de sentido contrario. $N\text{'}=2m\Omega \frac{dx}{dt}$

• El peso mg del anillo y la reacción N de la varilla, no se han representado por que no influyen en el movimiento del anillo

La ecuación del movimiento en el Sistema de Referencia No Inercial (en rotación) de la varilla es

${\displaystyle \begin{array}{l}m\frac{d^{2}r}{d{t}^2}=m{\Omega }^{2}r-k\left(r-l_0\right)\\ \frac{d^{2}r}{d{t}^2}+\left({\omega }_0^2-{\Omega }^2\right)r={\omega }_0^2{l}_0\\ \frac{d^{2}r}{d{t}^2}+{\omega }^{2}r={\omega }_0^2{l}_0\end{array}}$

La solución particular es una constante C, introduciendo en la ecuación diferencial

${\displaystyle \begin{array}{l}{\omega }^{2}C={\omega }_0^2{l}_0\\ C=\frac{{\omega }_0^2}{{\omega }^2}{l}_0\end{array}}$

La solución completa (homogénea+particular) de la ecuación diferencial es

• Si Ω<ω₀

${\displaystyle r=A\cos \left(\omega t\right)+B\sin \left(\omega t\right)+\frac{{\omega }_0^2}{{\omega }^2}{l}_0}$

donde los coeficientes A y B se determinan a partir de las condiciones iniciales. Si el anillo parte del reposo dr/dt=0 en el instante t=0, entonces B=0

${\displaystyle r=A\cos \left(\omega t\right)+\frac{{\omega }_0^2}{{\omega }^2}{l}_0}$

• Si Ω=ω₀

La aceleración es constante, tenemos un movimiento uniformemente acelerado

${\displaystyle \begin{array}{l}\frac{d^{2}r}{d{t}^2}={\omega }_0^2{l}_0\\ r=\frac{1}{2}{\omega }_0^2{l}_0{t}^2\end{array}}$

• Si Ω>ω₀

La ecuación diferencial es

${\displaystyle \frac{d^{2}r}{d{t}^2}-{\beta }^{2}r={\omega }_0^2{l}_0,{\beta }^2={\Omega }^2-{\omega }_0^2}$

La solución particular es una constante C, introduciendo en la ecuación diferencial

${\displaystyle \begin{array}{l}-{\beta }^{2}C={\omega }_0^2{l}_0\\ C=-\frac{{\omega }_0^2}{{\beta }^2}{l}_0\end{array}}$

La solución completa de la ecuación diferencial es

${\displaystyle r=A\exp \left(\beta t\right)+B\exp \left(-\beta t\right)-\frac{{\omega }_0^2}{{\beta }^2}{l}_0}$

donde los coeficientes A y B se determinan a partir de las condiciones iniciales. Si el anillo parte del reposo dr/dt=0 en el instante t=0, entonces A=B

${\displaystyle r=2A\cosh \left(\beta t\right)-\frac{{\omega }_0^2}{{\beta }^2}{l}_0}$

La distancia radial se incrementa exponencialmente con el tiempo

La trayectoria en el Sistema de Referencia No Inercial es rectilínea a lo largo del eje X'. Hemos calculado la distancia r al origen en el instante t

Trayectoria en el Sistema de Referencia Inercial

Conocida la posición (x', y') de la partícula en el Sistema de Referencia No Inercial, la posición (x, y) de la partícula en el Sistema de Referencia Inercial es

${\displaystyle \{\begin{array}{l}x=x\text{'}\cos (\Omega t)-y\text{'}\sin (\Omega t)\\ y=x\text{'}\sin (\Omega t)+y\text{'}\cos (\Omega t)\end{array}}$

En este caso, x'=r e y'=0

${\displaystyle \{\begin{array}{l}x=r\cos (\Omega t)\\ y=r\sin (\Omega t)\end{array}}$

Cuando Ω<ω₀

La partícula oscila en el eje X'. Las órbitas que describe en el plano XY serán cerradas si Ω/ω es un número racional α=p/q.

${\displaystyle \begin{array}{l}\frac{\Omega }{\omega }=\alpha \\ \frac{\Omega }{\sqrt{{\omega }_0^2-{\Omega }^2}}=\alpha \\ \Omega =\frac{\alpha }{\sqrt{1+{\alpha }^2}}{\omega }_0,\omega =\frac{1}{\sqrt{1+{\alpha }^2}}{\omega }_0\end{array}}$

LLamamos θ=Ωt, La trayectoria x, y del anillo es

${\displaystyle \begin{array}{l}r=A\cos \left(\frac{\Omega }{\alpha }t\right)+\left(1+{\alpha }^2\right)l_0\\ r=A\cos \left(\frac{1}{\alpha }\theta \right)+\left(1+{\alpha }^2\right)l_0\\ \{\begin{array}{l}x=r\cos (\theta )\\ y=r\sin (\theta )\end{array}\end{array}}$

Velocidad radial

La velocidad en la dirección radial es

${\displaystyle \frac{dr}{dt}=-\frac{\Omega }{\alpha }A\sin \left(\frac{\Omega }{\alpha }t\right)}$

La velocidad radial se hace nula en las posiciones de retorno, θ=Ωt=nπα

• Cuando n es par el coseno es positivo, la máxima distancia al origen es

${\displaystyle r_{máx}=A+\left(1+{\alpha }^2\right)l_0}$

• Cuando n es impar el coseno es negativo, la mínima distancia al origen es

${\displaystyle r_{\min }=-A+\left(1+{\alpha }^2\right)l_0}$

Periodo

El anillo parte de la posición θ=0, r=A+(1+α²)l₀ y regresará a dicha posición despues de n vueltas θ=2nπ

${\displaystyle \begin{array}{l}A\cos \left(\frac{1}{\alpha }2n\pi \right)+\left(1+{\alpha }^2\right)l_0=A+\left(1+{\alpha }^2\right)l_0\\ \cos \left(\frac{q}{p}2n\pi \right)=1\\ \frac{q}{p}2n\pi =2m\pi \\ qn=pm\end{array}}$

Donde q, p, n y m son enteros. Cuando m=q, entonces n=p

La trayectoria se repite cuando el ángulo θ=2pπ, como podemos comprobar en los ejemplos

Cuando Ω>ω₀

${\displaystyle \begin{array}{l}\frac{\Omega }{\beta }=\alpha \\ \frac{\Omega }{\sqrt{{\Omega }^2-{\omega }_0^2}}=\alpha \\ \Omega =\frac{\alpha }{\sqrt{{\alpha }^2-1}}{\omega }_0,\beta =\frac{1}{\sqrt{{\alpha }^2-1}}{\omega }_0\end{array}}$

La partícula describe una espiral logarítmica

${\displaystyle r=2A\cosh \left(\frac{1}{\alpha }\theta \right)-\left({\alpha }^2-1\right)l_0}$

Ejemplos, Ω<ω₀

Este es el código del program del script que dibuja las trayectorias en el Sistema Inercial de Referencia para Ω<ω₀

p=1; %número entero
q=3; %número entero
alfa=p/q; %número racional
l0=0.5; %longitud del muelle sin deformar
A=1; %amplitud
r=@(t) A*cos(t/alfa)+(1+alfa^2)*l0;
x=@(t) r(t).*cos(t);
y=@(t) r(t).*sin(t);
fplot(x,y,[0,2*pi*p])
grid on
axis equal
xlabel('x')
ylabel('y')
title('Trayectorias')

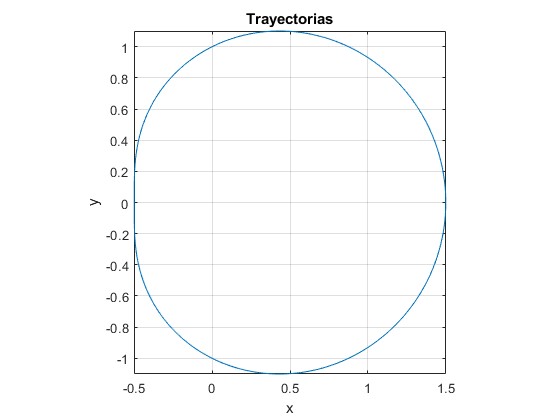
• p=1, q=1, l₀=0.5

• A=2



• A=1



• A=0.5



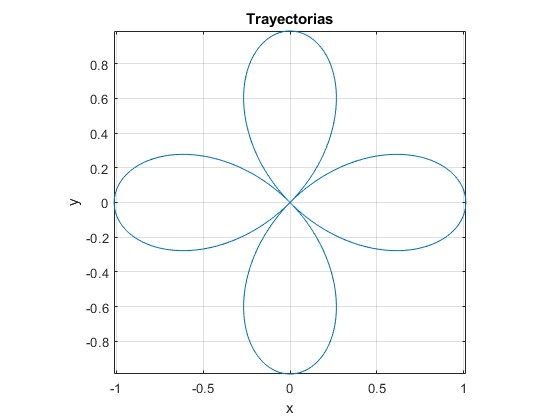
• l₀=0.01, A=1, p=1

• q=2.



• q=3



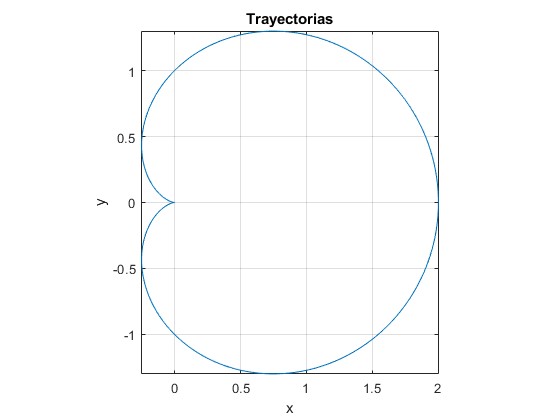
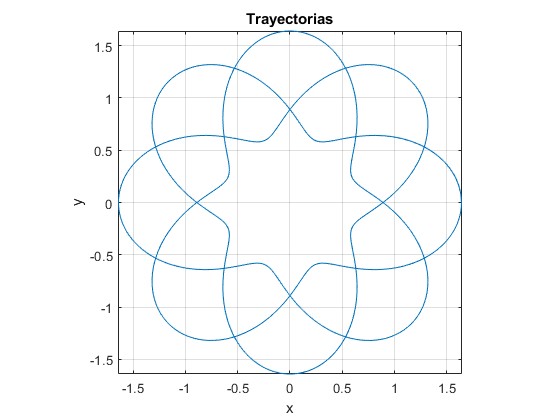
• l₀=1, A=0.5, p=3

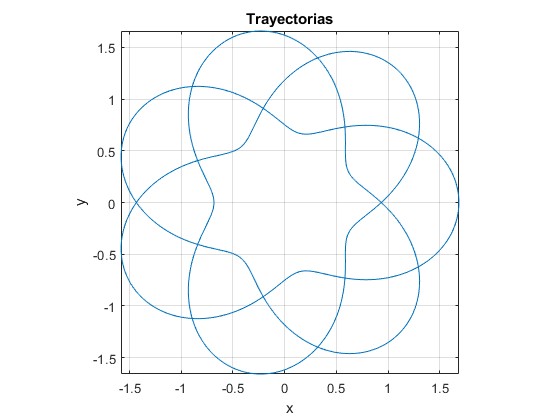
• q=8



• q=7



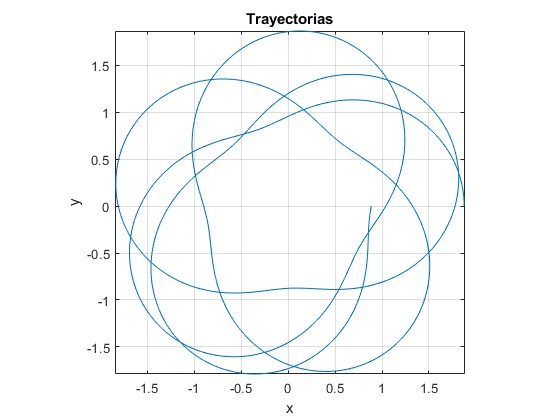
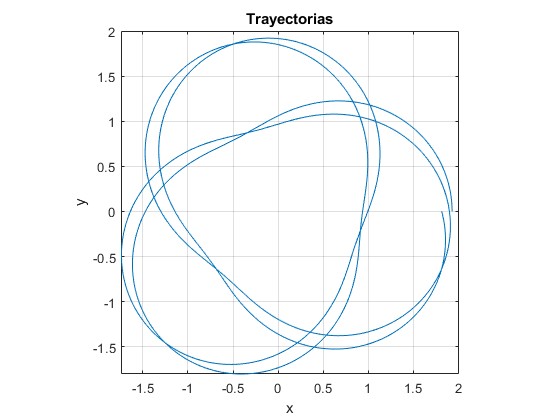
• Trayectorias abiertas. l₀=1, A=0.5

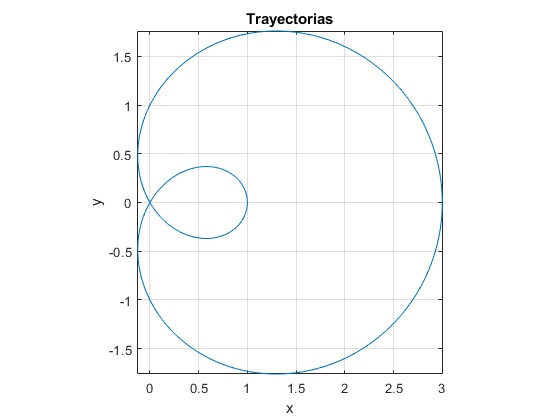
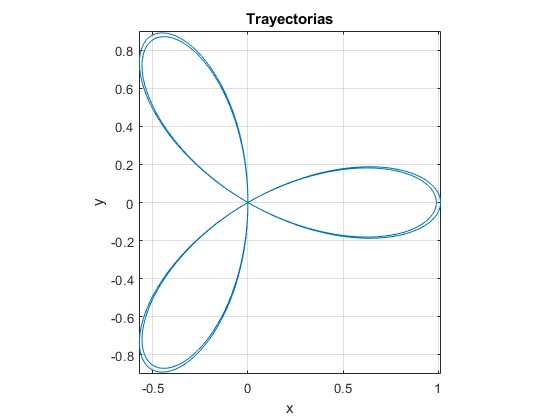
alfa=sqrt(3/7); 
l0=1;
A=0.5;
r=@(t) A*cos(t/alfa)+(1+alfa^2)*l0;
x=@(t) r(t).*cos(t);
y=@(t) r(t).*sin(t);
fplot(x,y,[0,8*pi])
grid on
axis equal
xlabel('x')
ylabel('y')
title('Trayectorias')

• $\alpha =\sqrt{\frac{3}{8}}$



• $\alpha =\sqrt{\frac{3}{7}}$

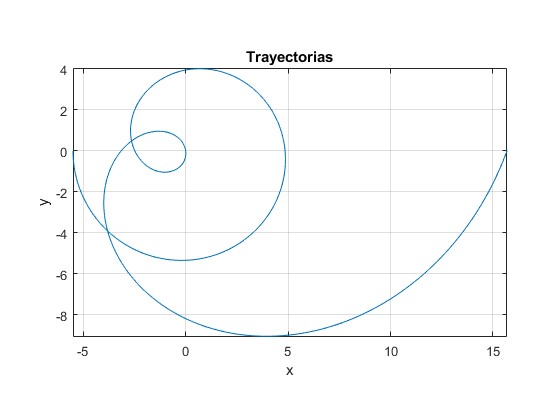
Ejemplos, Ω>ω₀

Este es el código del program del script que dibuja las trayectorias en el Sistema Inercial de Referencia para Ω>ω₀

alfa=4;
l0=0.5;
A=1;
r=@(t) 2*A*cosh(t/alfa)-(alfa^2-1)*l0;
x=@(t) r(t).*cos(t);
y=@(t) r(t).*sin(t);
fplot(x,y,[0,4*pi])
grid on
axis equal
xlabel('x')
ylabel('y')
title('Trayectorias')

Actividades

Para el caso Ω<ω₀. Se introduce

• La amplitud, A en el control titulado Amplitud
• La longitud del muelle sin deformar, l₀ en el control titulado Longitud
• El numerador p del número racional, en el control titulado numerador
• El ndenominador q del número racional, en el control titulado denominador

Se pulsa el botón titulado Nuevo

Probar con los siguientes valores

Referencias

L Motta, R Dutra, L Pereira, A Faria, M V Silveira, A C F Santos. A mechanical model for polar curves. Eur. J. Phys. 45 (2024) 045002