Movimiento en un pozo de potencial

La energía de una partícula bajo la acción de una fuerza central y conservativa de potencial V(r) es

$E = \frac{1}{2} m {(\frac{d r}{d t})}^{2} + \frac{L^{2}}{2 m r^{2}} + V (r)$

Vamos a estudiar el movimiento de una partícula en el potencial

$V (r) = {\begin{cases} - U_{0}, r < R \\ 0, r \geq R \end{cases}$

Representamos la energía potencial efectiva

$E_{e f} (r) = \frac{L^{2}}{2 m r^{2}} + V (r)$

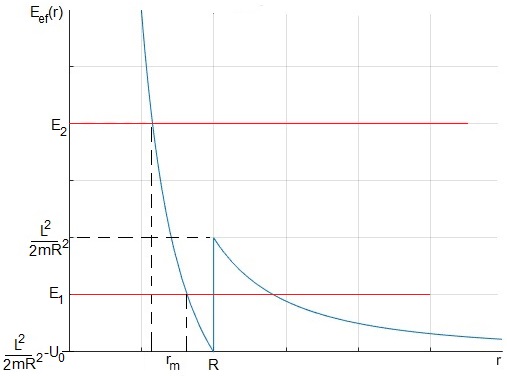
Para dibujar parte de esta figura hemos utilizado el código

R=1; %radio región circular
U0=1; %potencial constante
f=@(x) (1./x.^2-U0).*(x<R)+(1./x.^2).*(x>=R);
line([0,3],[2,2],'color','r')
line([0,3],[0.5,0.5],'color','r')
fplot(f,[0.5,3])
xlim([0,3])
grid on
xlabel('r')
ylabel('E_{ef}(r)')
title('Energía potencial efectiva')

Vemos que hay dos posibles casos:

Cuando la energía de la partícula $\frac{L^{2}}{2 m R^{2}} - U_{0} < E \leq \frac{L^{2}}{2 m R^{2}}$ , la partícula está confinada en el pozo de potencial de radio R, la distancia de mayor aproximación es r_m y la de menor es R
Cuando la energía de la partícula $E > \frac{L^{2}}{2 m R^{2}}$ , la partícula se puede mover desde el infinito hasta la distancia de mayor aproximación r_m

La posición de máximo acercamiento al origen r_m se calcula cuando la componente radial de la velocidad es nula dr/dt=0, la raíz positiva de

$\begin{array}{l} E = \frac{L^{2}}{2 m r_{m}^{2}} - U_{0} \\ r_{m} = \frac{L}{\sqrt{2 m (E + U_{0})}} \end{array}$

En esta página, estudiaremos los dos casos, empezando por el primero

Movimiento en el pozo de potencial

La partícula se puede mover en el anillo de radio interior r_m y de radio exterior R

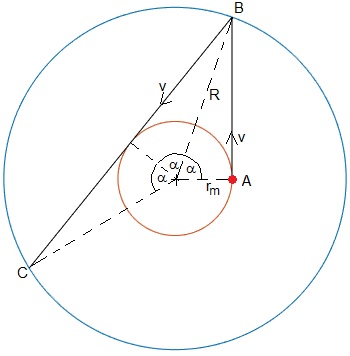
Para dibujar parte de esta figura se ha utilizado el código

R=1; %radio región circular
rm=R/3;  %radio interior
hold on
fplot(@(t) R*cos(t), @(t) R*sin(t), [0,2*pi])
fplot(@(t) rm*cos(t), @(t) rm*sin(t), [0,2*pi])
alfa=acos(rm/R);
line([rm,rm],[0,R*sin(ang)],'color','k')
line([rm,R*cos(3*alfa)],[R*sin(alfa),R*sin(3*alfa)],'color','k')
hold off
axis equal
axis off

Supongamos que la partícula de masa sale de la posición A (r_m,0) con velocidad v

La partícula se mueve con velocidad constante (la fuerza es nula), hasta que su distancia al origen es R, en la posición B (Rcosα, Rsinα), donde cosα=r_m/R. Se refleja en B, continúa su movimiento uniforme hasta que llega a C (Rcos(3α), Rsin(3α)) y así, sucesivamente

Determinamos la ecuación de la trayectoria a partir de la conservación de la energía y la constancia del momento angular

${\begin{cases} E = \frac{1}{2} m {(\frac{d r}{d t})}^{2} + \frac{L^{2}}{2 m r^{2}} - U_{0} \\ L = m r^{2} \frac{d θ}{d t} \end{cases}$

En la ecuación de la energía, sustituimos dr/dt

$\frac{d r}{d t} = \frac{d r}{d θ} \frac{d θ}{d t} = \frac{d r}{d θ} \frac{L}{m r^{2}}$

Despejamos dθ/dr para obtener la ecuación de la trayectoria

$\frac{d θ}{d r} = \frac{\frac{L}{m r^{2}}}{\sqrt{\frac{2}{m} (E - \frac{L^{2}}{2 m r^{2}} + U_{0})}}$

Para integrar se hace el cambio u=1/r

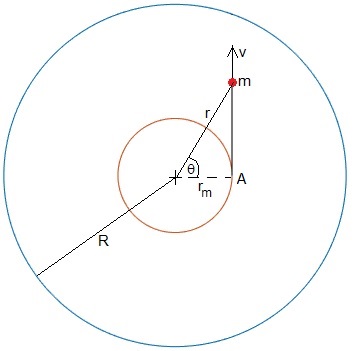
$\begin{array}{l} θ - θ_{0} = \frac{L}{\sqrt{2 m}} \int \frac{- d u}{\sqrt{E - \frac{L^{2}}{2 m} u^{2} + U_{0}}} \\ θ - θ_{0} = \int \frac{- d u}{\sqrt{(E + U_{0}) \frac{2 m}{L^{2}} - u^{2}}} = \arccos (\frac{L}{\sqrt{2 m (E + U_{0})}} u) \\ \frac{r_{m}}{r} = \cos (θ - θ_{0}) \end{array}$

Como apreciamos en la figura, la ecuación de la trayectoria de la partícula que parte de A es cosθ=r_m/r, hasta que llega a la posición B a una distancia R del origen. El ángulo máximo α se obtiene cuando r=R, cosα=r_m/R

El código, representa la trayectoria de la partícula en un pozo de potencial de radio R. Tomamos r_m=2R/3

R=1; %radio región circular
rm=2*R/3;  %radio interior
hold on
fplot(@(t) R*cos(t), @(t) R*sin(t), [0,2*pi])
fplot(@(t) rm*cos(t), @(t) rm*sin(t), [0,2*pi])
alfa=acos(rm/R);
line([rm,rm],[0,R*sin(alfa)],'color','k')
line([rm,R*cos(3*alfa)],[R*sin(alfa),R*sin(3*alfa)],'color','k')
for k=3:2:9
    line([R*cos(k*alfa),R*cos((k+2)*alfa)],[R*sin(k*alfa),R*sin((k+2)*alfa)]
,'color','k')
end
hold off
axis equal
grid on
xlabel('x')
ylabel('y')
title('Pozo de potencial')

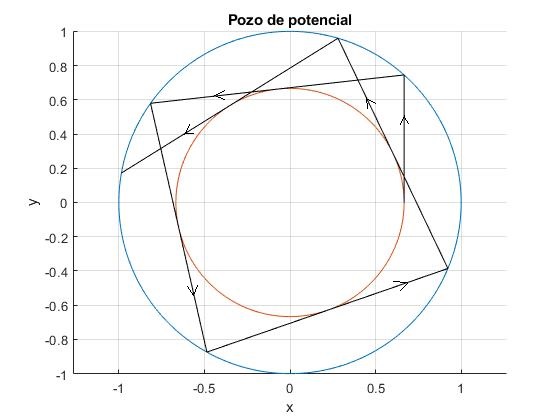
Dispersión de las partículas por el pozo de potencial

Estudiamos la dispersión por el potencial V(r) para las partículas de masa m y velocidad v₀ tal que su energía

$E = \frac{1}{2} m v_{0}^{2} > \frac{L^{2}}{2 m R^{2}}$

Dibujamos la trayectoria de una partícula cuyo parámetro de impacto b<R

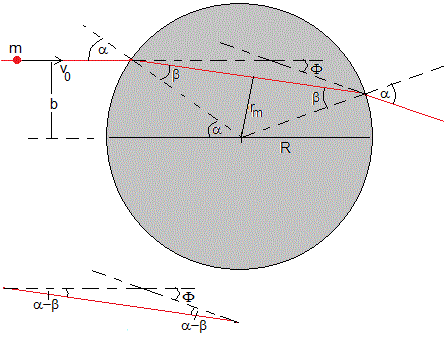
El punto de máximo acercamiento al origen r_m se obtiene cuando la componente radial de la velocidad es nula dr/dt=0. Teniendo en cuenta que el momento angular L=mbv₀

$\begin{array}{l} \begin{array}{l} E = \frac{{(b m v_{0})}^{2}}{2 m r_{m}^{2}} - U_{0} \\ E = E \frac{b^{2}}{r_{m}^{2}} - U_{0} \end{array} \\ r_{m} = b \sqrt{\frac{E}{E + U_{0}}} \end{array}$

Por la ley de la refracción, sinα=nsinβ, es decir, b/R=n·r_m/R. De esta forma relacionamos una propiedad óptica (índice de refracción) con una propiedad mecánica el potencial U₀ y la energía E de las partículas

$n = \sqrt{\frac{E + U_{0}}{E}}$

El principio de conservación de la energía se escribe

$\frac{1}{2} m v_{0}^{2} = \frac{1}{2} m v^{2} + (- U_{0})$

De la definición de índice de refracción

$\begin{array}{l} n^{2} \frac{1}{2} m v_{0}^{2} = \frac{1}{2} m v_{0}^{2} + U_{0} = \frac{1}{2} m v^{2} \\ n v_{0} = v \end{array}$

Siendo v₀ la velocidad de la partícula para r≥R y v su velocidad para r<R

Vamos a establecer la relación entre el ángulo de dispersión Φ (ángulo entre la dirección inicial y final de la velocidad) y el parámetro de impacto b. En la parte inferior de la figura, vemos que 2(α-β)+180-Φ=180, Φ=2(α-β)

$\begin{array}{l} \sin α = n \sin β \\ \frac{b}{R} = n \sin (α - \frac{Φ}{2}) \\ \frac{b}{R} = n (\sin α \cos \frac{Φ}{2} - \cos α \sin \frac{Φ}{2}) \\ \frac{b}{R} = n \frac{b}{R} \cos \frac{Φ}{2} - n \sqrt{1 - \frac{b^{2}}{R^{2}}} \sin \frac{Φ}{2} \\ \frac{b}{R} (n \cos \frac{Φ}{2} - 1) = n \sqrt{1 - \frac{b^{2}}{R^{2}}} \sin \frac{Φ}{2} \end{array}$

Elevando al cuadrado y despejando b/R

$\frac{b}{R} = \frac{n \sin \frac{Φ}{2}}{\sqrt{n^{2} + 1 - 2 n \cos \frac{Φ}{2}}}$

Trayectoria

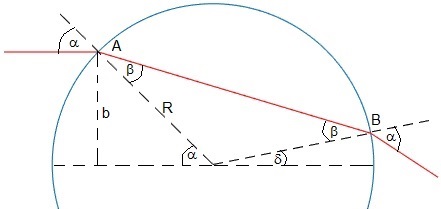
Representamos la trayectoria de una partícula para un índice de refracción n=2 y parámetro de impacto b=0.7. El radio R=1

Dado el parámetro de impacto b, calculamos el ángulo α, sinα=b/R. Dado el índice de refracción, calculamos el ángulo β, sinβ=sinα/n
Trazamos una recta horizontal de altura b hasta su intersección A con la circunferencia de radio R
La recta que atraviesa la región circular, parte del punto A (-Rcosα, b) y llega al punto B (Rcosδ, Rsinδ). Donde el ángulo δ=180-α-(180-2β)=2β-α
Finalmente, trazamos la recta que parte de este punto y forma un ángulo α con la dirección radial que pasa por dicho punto

Para trazar la trayectoria (líneas de color rojo) se ha utilizado el código

R=1; %radio región circular
b=0.7; %parámetro de impacto
n=1.5; %índice de refracción
fplot(@(t) R*cos(t), @(t) R*sin(t), [0,2*pi])
alfa=asin(b/R);
line([-1.3,-R*cos(alfa)],[b,b],'color','r')
beta=asin(b/(n*R));
delta=2*beta-alfa;
line([-R*cos(alfa),R*cos(delta)],[b,R*sin(delta)],'color','r') 
line([R*cos(delta),R*cos(delta)+0.5*cos(delta-alfa)],
[R*sin(delta),R*sin(delta)+0.5*sin(delta-alfa)],'color','r')
line([0,-R*cos(alfa)],[0,b],'lineStyle','--','color','k')
line([0,R*cos(delta)],[0,R*sin(delta)],'lineStyle','--','color','k')
axis equal
axis off

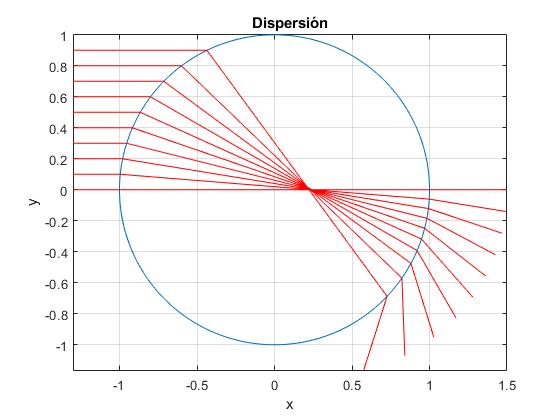
dado el índice de refracción n, trazamos las trayectorias de las partículas para varios parámetros de impacto

R=1; %radio región circular
n=5; %índice de refracción
fplot(@(t) R*cos(t), @(t) R*sin(t), [0,2*pi])
for b=0:0.1:0.9 %parámetros de impacto
    alfa=asin(b/R);
    line([-1.3,-R*cos(alfa)],[b,b],'color','r')
    beta=asin(b/(n*R));
    delta=2*beta-alfa;
    line([-R*cos(alfa),R*cos(delta)],[b,R*sin(delta)],'color','r') 
    line([R*cos(delta),R*cos(delta)+0.5*cos(delta-alfa)],
[R*sin(delta),R*sin(delta)+0.5*sin(delta-alfa)],'color','r')
end
grid on
axis equal
xlabel('x')
ylabel('y')
title('Dispersión')

Actividades

Se introduce

El índice de refracción n, en el control titulado Indice de refracción
El radio de la región circular se ha fijado en R=10
La velocidad de la partícula fuera de la región circular, r<R se ha fijado en v₀=1

Se pulsa el botón titulado Nuevo y a continuación, ►

Observamos el movimiento de las partículas cuya velocidad inicial v₀ es paralela al eje X, su trayectoria rectilínea con velocidad v=n·v₀ dentro de la región circular y cuando sale de la misma con la misma velocidad v₀ inicial.

Indice de refracción:

Referencias

Alain J. Brizard, An Introduction to Lagrangian Mechanics, pp. 108-110, 127-129